BLOQUE 2

De volúmenes y áreas Múltiplos y submúltiplos del metro cuadrado y del metro cúbico 1. La pecera para los peces tropicales de un acuario tiene la forma de un cubo de 1 m por lado. Si se aumenta 1 cm a cada lado de la pecera, ¿cuántos litros adicionales de agua crees que le quepan? Imagínate el tamaño de la pecera; para eso, identifica una longitud en tu salón que mida 1 m; ahora piensa en un cubo de 1 m por lado y compáralo con 1 cm. Haz una estimación del agua adicional que puede entrar en la pecera agrandada, ¿será menos de 1 litro? _____________ ¿entre 1 y 5 litros? _________________ ¿entre 5 y 10 litros?_________________ ¿más de 10 litros? 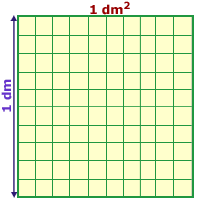__________________ Ahora calcula, ¿cuál es el área de la base de la pecera original en m2?_____________________________________________________ ¿y en dm2?____________________ ¿y en cm2?___________________ Recuerda que 1 m2 es el área de un cuadrado que mide 1 m por lado. ¿Qué es 1 dm2?__________________¿y 1 cm2? __________________ ¿Cuál es el volumen de la pecera original en m3? 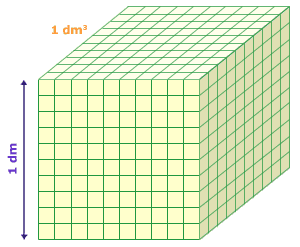____________________ ¿y en dm3?____________________ ¿y en cm3?___________________ Recuerda que 1 m3 es el volumen de un cubo que mide 1 m de arista. ¿Qué es 1 dm3? ______________________ ¿y 1 cm3? _________________ ¿Cuánto aumenta el área de la base de la pecera al aumentar 1 cm a sus lados? ___________________________________________________ ¿Cuánto aumenta su volumen? ________________________________ Un litro de agua ocupa un volumen de 1 dm3, ¿cuántos litros de agua contiene la pecera original? __________________________________________ ¿Cuántos litros contiene la pecera agrandada? _____________________ Compara esto con tu estimación inicial. 2. Forma equipos de 3 o 4 compañeros y busca una regla para convertir los múltiplos y submúltiplos del metro cuadrado (m2) y del metro cúbico (m3). Fíjate en las figuras que muestran 1 dm2 y 1 dm3. 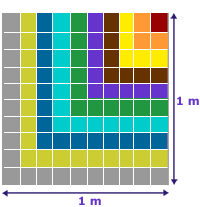Ayúdate también completando las tablas siguientes: 3. El piso de una guardería se va a recubrir con mosaicos de colores de 1 dm de lado. Cada metro cuadrado deberá tener la combinación de colores que se muestra a continuación. ¿Cuántos mosaicos tiene en total el diseño? _________________________________ ¿Cuántos mosaicos hay de cada color? _________________________________ Completa la siguiente tabla. Fíjate en los números que escribiste en la tabla, ¿qué tipo de números son? ________________________________ Contesta las siguientes preguntas sin hacer las operaciones, fíjate sólo en la figura. ¿Cuánto vale la suma de estos números? _________________________________ ¿Cuánto vale la suma de los 4 primeros números impares? _________________________________ ¿Cuánto vale la suma de los 7 primeros números impares? _________________________________ ¿Cuánto crees que vale la suma de los 12 primeros números impares? _________________________________ Enuncia una regla para encontrar la suma de una serie de números impares que comienza con el uno. Comenta tus respuestas con tus compañeros y tu maestro.