IV. EL ESPACIO-TIEMPO CURVO

SI BIEN la mec�nica de Newton es el fundamento de la f�sica cl�sica, deja de ser v�lida en circunstancias que desbordan el marco de la experiencia cotidiana; en particular, cuando se consideran velocidades cercanas a la de la luz. La misma teor�a electromagn�tica, desarrollada por James C. Maxwell en el siglo pasado, no encajaba en la f�sica newtoniana, por lo que, al empezar el siglo XX, se hizo necesaria una reformulaci�n de la f�sica.

Fue as� como, en 1905, Albert Einstein (Figura 25) formul� la Teor�a de la Relatividad Especial, que vino a revolucionar todas nuestras concepciones cient�ficas y filos�ficas. Aunque tard� varios a�os en ser reconocida por los dem�s cient�ficos, esta teor�a es actualmente uno de los pilares m�s s�lidos de la f�sica moderna.

Figura 25. Albert Einstein.

En la Relatividad Especial, el espacio y el tiempo no son dos categor�as independientes, como en la f�sica newtoniana. Por el contrario, el mundo en el que vivimos se concibe como un espacio de cuatro dimensiones: tres del espacio com�n, m�s el tiempo interpretado como una cuarta dimensi�n. En la teor�a de Einstein, no existe un tiempo absoluto, sino que el tiempo depende del movimiento de quien lo mide. Otro efecto inesperado, predicho por esta teor�a, es que la velocidad de la luz es la misma con respecto a cualquier observador, independientemente de la velocidad con que �ste se mueva; la velocidad de la luz —designada com�nmente por la letra c— es una constante fundamental de la naturaleza.¹ Einstein tambi�n predijo una equivalencia entre la masa y la energ�a tal que, bajo condiciones apropiadas, una puede transformarse en la otra seg�n la famosa f�rmula:

E = mc2

(E: energ�a, m: masa). Lo cual se confirm� en forma dram�tica a�os despu�s.

Las fuerzas electromagn�ticas se pod�an describir de una manera muy natural con el formalismo de la teor�a de Einstein, hecha a la medida para ellas, pero la fuerza gravitacional segu�a eludiendo toda descripci�n relativista. La teor�a de la gravitaci�n de Newton funciona perfectamente para objetos con velocidades peque�as con respecto a la luz, pero no toma en cuenta la acci�n de la gravedad sobre la luz misma. Dicha acci�n es imperceptible en nuestra experiencia cotidiana, pero no siempre es despreciable en el Universo (el ejemplo m�s espectacular es el de los hoyos negros, que son cuerpos cuya intens�sima atracci�n gravitacional no deja escapar la luz). Y dado que la trayectoria de un rayo luminoso parece un ejemplo natural de "l�nea recta", es de esperarse que un campo gravitacional intenso altere muy peculiarmente nuestras concepciones geom�tricas.

En 1915, Albert Einstein formul� la teor�a de la Relatividad General, as� llamada porque generaliz� la Teor�a Especial para incluir los efectos de la gravitaci�n. Con esta teor�a sacudi� nuevamente los fundamentos de la f�sica cl�sica. Seg�n el postulado m�s revolucionario de la Relatividad General, el espacio en el que vivimos es curvo y la gravitaci�n es la manifestaci�n de esta curvatura.

Un ejemplo de espacio curvo es la superficie de la Tierra; es un espacio de dos dimensiones, en el sentido de que la posici�n de un punto en �l se describe por medio de dos coordenadas: la longitud y la latitud (Figura 26). Para comprender las implicaciones geom�tricas de la curvatura, imaginemos un ge�metra que decide comprobar en la pr�ctica algunos de los postulados fundamentales de la geometr�a cl�sica: por ejemplo, el de que dos rectas que se cruzan en un punto no se vuelven a cruzar (Figura 27). Supongamos que, para ello, se pasa d�as y noches trazando rectas sobre el papel, tratando de encontrar un par de ellas que se crucen en dos o m�s puntos. La b�squeda resulta vana, pero, lejos de darse por vencido, el ge�metra decide hacer sus comprobaciones a gran escala, trazando rectas de varios miles de kil�metros. El primer problema al que se enfrenta es el de precisar el concepto de "recta" a una escala tan grande. Siendo la Tierra redonda, una "recta" trazada sobre su superficie necesariamente es una curva y ese efecto se hace notable mientras m�s grandes son los tama�os considerados. Pero el problema tiene una soluci�n muy simple: se define una "recta" como la distancia m�s corta entre dos puntos. Volviendo a nuestro ge�metra, supongamos que traza dos "rectas" de varios miles de kil�metros que originalmente se cruzan en un punto. Esas dos rectas son en realidad segmentos de c�rculos y se volver�n a cruzar en el otro lado de la Tierra (Figura 28). Lo mismo suceder� con otros postulados de la geometr�a cl�sica (por un punto dado s�lo pasa una recta paralela a otra recta dada; dos rectas paralelas entre s� nunca se cruzan; los tres �ngulos de un tri�ngulo suman siempre 180 grados; etc.). Estos postulados son v�lidos a escalas peque�as, pero nuestro ge�metra comprobar� que dejan de aplicarse a escalas comparables con el di�metro de la Tierra. De hecho, el ge�metra habr� descubierto la curvatura de la Tierra.

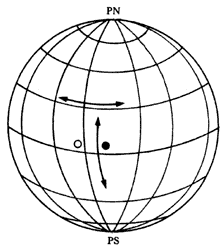
Figura 26. La longitud y la latitud son dos coordenadas con las que se puede localizar cualquier punto sobre la superficie terrestre.

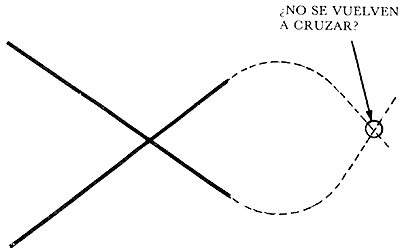
Figura 27. Seg�n la geometr�a cl�sica, dos rectas que se cruzan en un punto no vuelven a cruzarse.

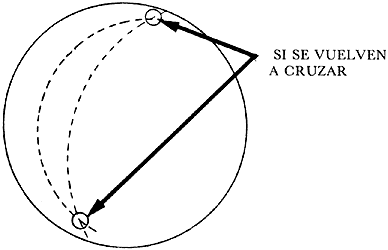
Figura 28. Pero dos "rectas" s� se cruzan sobre una superficie curva.

Supongamos ahora que nuestro imaginario ge�metra, provisto de una nave espacial, decide continuar sus experimentos en el Sistema Solar. Puede utilizar como rectas los haces luminosos de un l�ser. Encontrar� que los postulados de la geometr�a cl�sica dejan de aplicarse otra vez, aunque, en este caso, la desviaci�n ser� m�nima y s�lo podr� ser descubierta por mediciones extremadamente precisas.

Pero si el ge�metra encuentra la manera de proseguir sus experimentos a escalas cada vez mas grandes, hasta cubrir el Universo mismo, comprobar� que los postulados de la geometr�a cl�sica dejan de aplicarse cada vez m�s dr�sticamente: las rectas se cruzan en m�s de un punto, las paralelas se unen o separan, la suma de los �ngulos de un tri�ngulo de dimensiones c�smicas no da 180 grados, etc. En resumen, habr� descubierto la curvatura del Universo.

Einstein descubri� que el Universo es curvo, pero, a diferencia del hipot�tico ge�metra, lleg� a esa conclusi�n por medio de razonamientos l�gicos combinados con experiencias f�sicas. M�s a�n, la causa de la curvatura es la masa, y la curvatura del espacio se manifiesta como fuerza gravitacional. Adem�s, la masa de los cuerpos no s�lo deforma el espacio sino tambi�n el tiempo: cerca de un cuerpo muy masivo el tiempo transcurre m�s lentamente.

Si el Sol atrae a los planetas, es porque deforma el espacio-tiempo a su alrededor y los planetas se mueven siguiendo esa curvatura, al igual que una canica que se mueve sobre una superficie curvada (Figura 29). Pero si bien es f�cil visualizar la curvatura de la superficie terrestre o cualquier otra superficie contenida en el espacio "com�n" de tres dimensiones, la curvatura del espacio-tiempo no puede visualizarse como si estuviera contenida en un espacio m�s amplio de cinco o m�s dimensiones.

Figura 29. Un cuerpo masivo deforma el espacio-tiempo a su alrededor.

Afortunadamente, un espacio de cualquier n�mero de dimensiones, aunque escape a nuestra experiencia e intuici�n, puede estudiarse por medio de f�rmulas matem�ticas. En el siglo XIX, matem�ticos como Riemann y Lobashevski elaboraron nuevas geometr�as, perfectamente autoconsistentes, pero que no satisfac�an algunos de los postulados de la geometr�a cl�sica. En particular, Riemann desarroll� un formalismo matem�tico que permiti� estudiar espacios curvos con cualquier n�mero de dimensiones.

Durante varias d�cadas, la geometr�a riemanniana fue considerada como una simple especulaci�n matem�tica, sin conexi�n con la realidad, hasta que Einstein vio en ella la herramienta matem�tica necesaria para su teor�a de la gravitaci�n. Con la teor�a de la Relatividad General, el espacio y el tiempo dejaron de ser simples escenarios de los fen�menos naturales, para transformarse en participantes din�micos.

La curvatura del espacio-tiempo es un efecto casi imperceptible en nuestro sistema planetario; esto no es de extra�arse, pues la fuerza de la gravitaci�n es extremadamente d�bil comparada con otras fuerzas de la naturaleza (basta recordar que, al levantar una piedra, nuestros m�sculos vencen la atracci�n gravitacional de toda la Tierra). Pero la magnitud sorprendente de la curvatura del espacio-tiempo se har� evidente a la escala del Universo mismo.²

El primer estudio te�rico del Universo dentro del marco de la Relatividad General se debe al mismo Einstein y data de 1917. Einstein parti� de dos suposiciones b�sicas: el Universo es homog�neo e is�tropo. Por homogeneidad se entiende que la materia en el Universo est� distribuida, a gran escala, en forma uniforme —tal como el gas en un recipiente, que se compone de mol�culas, s�lo que en el caso del Universo las mol�culas ser�an los c�mulos de galaxias—. Y por isotrop�a, que la apariencia del Universo, tambi�n a gran escala, es la misma en todas las direcciones. Estas dos suposiciones han sido confirmadas por las observaciones astron�micas (volveremos a ellas en los pr�ximos cap�tulos).

Einstein propuso un modelo cosmol�gico seg�n el cual el Universo era finito, pero sin fronteras. Esta concepci�n aparentemente contradictoria se aclara si recordamos que el espacio es curvo; as� como la superficie de la Tierra es finita, pero sin bordes, del mismo modo el universo de Einstein puede cerrarse sobre s� mismo y no tener fronteras. En el modelo propuesto por Einstein, una nave espacial que viaje siempre en la misma direcci�n regresar� a su punto de partida despu�s de atravesar todo el Universo, como un Magallanes c�smico.

Todav�a no se hab�a descubierto la expansi�n c�smica en 1917, por lo que Einstein supuso tambi�n que el Universo es est�tico, o sea, que no cambia con el tiempo. Pero las ecuaciones de la Relatividad General indicaban que el Universo no pod�a mantenerse est�tico, sino que se colapsar�a sobre s� mismo debido a su propia atracci�n gravitacional —tal como hab�a previsto Newton—. La �nica soluci�n que encontr� Einstein fue introducir en sus f�rmulas una peque�a modificaci�n que permit�a a la fuerza gravitacional volverse repulsiva a distancias c�smicas, y evitar as� el colapso del Universo.

Poco despu�s, alrededor de 1922, el f�sico ruso A. A. Friedmann estudi� m�s detalladamente las ecuaciones de Einstein, sin la modificaci�n introducida por �ste, y lleg� a la conclusi�n de que el Universo no pod�a permanecer inm�vil, sino que deb�a encontrarse en proceso de expansi�n. Dependiendo de la densidad de materia en el Universo, la expansi�n seguir�, ya sea indefinidamente o hasta un momento en que se detenga y empiece una contracci�n (Figura 30). Al principio, los trabajos de Friedmann no fueron tomados en serio, pero cuando Hubble descubri� la expansi�n c�smica, los f�sicos y astr�nomos se dieron cuenta de que dicho efecto hab�a sido predicho te�ricamente (Friedmann muri� de tifoidea en 1925 sin ver la confirmaci�n de su obra).

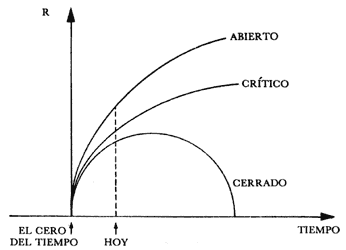
Figura 30. La evoluci�n del factor de escala R (la distancia entre dos galaxias) en funci�n del tiempo, seg�n las tres posibilidades descubiertas por Friedmann.

Independientemente de Friedmann, el abad belga Georges Lemaitre estudi� las ecuaciones de Einstein por su cuenta, pero incluyendo la repulsi�n c�smica, y lleg� a conclusiones semejantes a las del f�sico ruso. Lemaitre demostr� que el Universo est�tico de Einstein era inestable, en el sentido de que cualquier peque�a perturbaci�n provocar�a una expansi�n o contracci�n que no se detendr�a nunca. Basado en sus c�lculos, Lemaitre formul� la hip�tesis de que el Universo se encontraba originalmente en un estado de compresi�n tal que toda la materia formaba un solo y �nico n�cleo at�mico, que llenaba todo el espacio c�smico disponible: el �tomo primordial. Como esa configuraci�n era inestable, en alg�n momento el Universo empez� a expanderse; el �tomo primordial se rompi� en innumerables pedazos a partir de los cuales se formaron todos los elementos qu�micos en el Universo. A gran escala, la expansi�n del Universo se desarroll� esencialmente como en el modelo de Friedmann; a escala m�s peque�a, algunas regiones del �tomo primordial se expandieron m�s lentamente que otras, hasta detenerse y empezar a contraerse en alg�n momento para formar las galaxias.

En 1946, el f�sico Georges Gamow propuso que el Universo no s�lo se encontraba inicialmente a muy altas densidades, sino tambi�n a temperaturas extremadamente altas. Poco despu�s de iniciarse la expansi�n, la materia era una mezcla homog�nea de part�culas elementales: electrones, fotones, protones, neutrones, neutrinos, etc. Inicialmente, la temperatura era pr�cticamente infinita, pero, a medida que se expand�a el Universo, la materia se fue enfriando; cuando la temperatura baj� a unos mil millones de grados Kelvin, las condiciones fueron propicias para la creaci�n de los elementos qu�micos que componen el Universo. En los pr�ximos cap�tulos, estudiaremos con m�s detalle la teor�a de la Gran Explosi�n.

NOTAS

1 c= 299 792 kil�metros por segundo o, redondeando: c = 300 000 km/seg.

2 O cerca de objetos masivos extremadamente densos, como las estrellas de neutrones o los hoyos negros.