IV. LOS RELOJES NUCLEARES

YA SABEMOS que una de las características de la radiactividad es que la emisión de la radiación a y b necesariamente va asociada a la transformación de un elemento en otro. Por ejemplo, si un núcleo de un elemento de número atómico Z y número de neutrones N emite una partícula a, al perder dos protones y dos neutrones se convierte en un nuevo elemento con número atómico Z-2 y número de neutrones N-2. El número de masa A disminuye en cuatro unidades. En el caso de la emisión b, también sucede la correspondiente transmutación de elementos. La emisión g, aunque no implica cambio de un elemento en otro, sí va asociada al paso de un nivel energético a otro del mismo núcleo.

Esto significa que si uno comienza con una cantidad dada (por ejemplo, un gramo) del elemento radiactivo, llamado padre, después de un tiempo esta cantidad va disminuyendo y simultáneamente se va creando el nuevo elemento, el hijo. Dado suficiente tiempo, todos los núcleos del padre podrían desaparecer y transformarse en núcleos del hijo. La pregunta ahora es ¿cuánto tiempo se necesita?, o bien ¿con qué rapidez sucede el decaimiento de uno en otro?

Una manera de visualizar este proceso es imaginarse un reloj de arena. Si el paso de granos del recipiente superior al inferior es constante, decimos que su comportamiento es lineal y usando una gráfica como la de la figura 22 podemos saber el número de granos que ha caído, o bien el número que queda arriba en cualquier instante. En la figura 22 se gráfica número de granos contra tiempo. La línea continua representa el número de granos en el recipiente superior. En el instante que se inicia el proceso (t = 0), en el recipiente superior hay un número determinado de granos, que llamamos N₀. Al transcurrir el tiempo este número disminuye linealmente hasta que en un tiempo T ha caído a cero. Simultáneamente el número de granos en el recipiente inferior va desde cero en t = 0 hasta N₀ en t =T (línea discontinua en la misma figura). Es de notarse que si uno conoce N₀ y T, y sabe que el comportamiento es lineal, se puede conocer, para cualquier instante t, el número N_sup de granos en el recipiente superior, y N_inf, el número en el inferior.

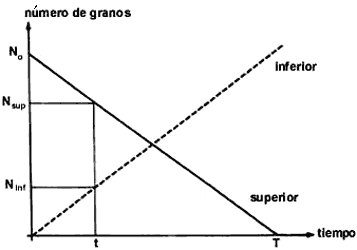
Figura 22. Un reloj de arena lineal.

Ahora bien, el decaimiento radiactivo de los núcleos no sigue un comportamiento lineal, sino exponencial representado en la figura 23. Aunque ahora las líneas que corresponden a la abundancia del elemento padre y del hijo son curvas, sigue siendo cierto que uno puede conocer cuánto del padre (N_padre) y cuánto del hijo (N_hijo) hay en un instante determinado. Desde luego es necesario saber de antemano con cuántos núcleos N₀ se inició el proceso (t = 0) y qué tan rápidamente cae la curva exponencial.

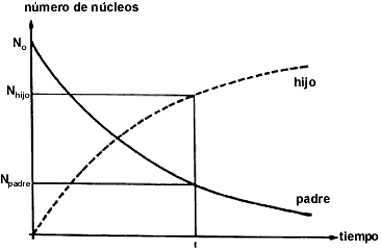
Figura 23. Decaimento exponencial de los núcleos.

La ley exponencial de decaimiento radiactivo sucede en virtud de que, a diferencia del reloj de arena, el paso de padre a hijo depende de cuántos núcleos del padre hay en cualquier instante. Cuanto menos núcleos del padre hay, menos se transforman en hijo. Es como si se tratase de un reloj de arena cuya abertura se fuera constriñendo con el tiempo. Otra manera de decirlo es que la probabilidad de decaimiento es constante.

Una cantidad característica del decaimiento exponencial de los núcleos es la vida media t_1/2. Es el tiempo que tarda el número de núcleos del elemento padre en reducirse a la mitad. En el decaimiento exponencial no importa con cuántos núcleos se comienza; siempre tarda el mismo tiempo en reducirse a la mitad. Esto se puede ver en la figura 24, en donde se representa el decaimiento de 10 000 núcleos de ¹⁴C (vida media t_1/2 X 5 730 años). En el lapso de una vida media, él número original se redujo a 5 000; en otro lapso igual se redujo a la mitad de 5 000, o sea a 2 500; en otro lapso igual a 1 250, y así sucesivamente: cada vez que transcurre una vida medía, el número se reduce a la mitad.

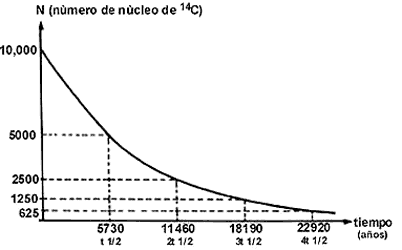
Figura 24. Curva de decaimento del ¹⁴C.

La ley exponencial no sólo se aplica al número de núcleos, sino también a la radiactividad de la muestra que los contiene. En la figura 24 bien podríamos haber graficado la actividad de la muestra en vez del número de núcleos. Esto es porque la actividad es proporcional al número de núcleos. Al reducirse éste, también disminuye la actividad.

La fórmula matemática que describe la ley exponencial de decaimiento es la siguiente:

N=N₀^e-lt.

En esta fórmula N representa el número de núcleos del padre en el instante t; N₀ es el número inicial cuando t = 0; l se denomina la constante de decaimiento; e es la base de los logaritmos naturales. La constante de decaimiento l representa la probabilidad de que haya decaimiento. Está relacionada con la vida media como sigue:

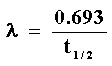
En otras palabras, la probabilidad de decaimiento es inversamente proporcional a la vida media. Cuanto mayor es l, más rápidamente decae y menos tiempo tarda.

Cada tipo de núcleo radiactivo tiene una vida media distinta, incluso a veces se mide la vida media para identificar el elemento. Las vidas medias de los núcleos radiactivos conocidos van desde fracciones de segundo hasta miles de millones de años. La figura 25 muestra el decaimiento de cuatro núcleos con vidas medias de 1, 5, 20 y 100 unidades. En el cuadro 5 se da una lista de algunos elementos radiactivos más importantes con sus vidas medias para ilustrar la gran diversidad de valores que se conocen.

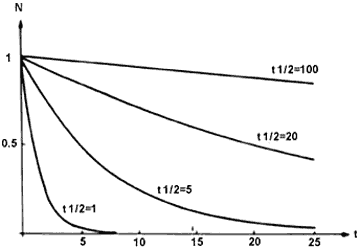
Figura 25. Ejemplos de curvas de decaimento de distintas vidas medias, 1, 5, 20 y 100 unidades de tiempo.

Cuadro 5. Algunos radioisótopos importantes y sus vidas medias.

Isótopo	Vida media
204Pb	1.4 x 1017 años
232Th	1.41 x 1010 años
87Rb	4.7 x 109 años
238U	4.51 x 109 años
40K	1.3 x 109 años
235U	7.13 x 108 años
14C	5730 años
226Ra	1600 años
137Cs	30 años
90Sr	28.8 años
3H (tritio)	12.26 años
60Co	5.24 años
210Po	138.4 días
32P	14.3 días
131I	8.05 días
222Rn	3.825 días
n (neutrón)	12 minutos
10C	19.4 segundos
26Na	1 segundo
5Li	10-21 de segundo

Es muy frecuente que el producto (el hijo) de un decaimiento sea a su vez radiactivo, generándose entonces nietos y otros descendientes hasta llegar a uno que sea estable. Se habla entonces de cadenas de decaimiento, las cuales pueden constar de más de una docena de pasos. Como ejemplo podemos citar la cadena del ²³⁸U, que sucede de modo natural (véase la Fig. 26). Cada círculo representa un núcleo y cada flecha un decaimiento a o b; la vida media de los integrantes de la cadena se muestra en el cuadro 6. En cadenas de este tipo el número N de cada integrante en un instante determinado sigue una ley mucho más complicada que la exponencial. Por ejemplo, tomemos el ²²²Rn, que se produce por el decaimiento de ²²⁶Ra —con vida media 1 620 años— y decae a su vez con vida media de 3.82 días. La cantidad de ²²²Rn va a estar, pues, más bien regida por su producción que por su decaimiento. En la cadena completa se establece un equilibrio dependiente de todas las vidas medias. Para ayudar a imaginarse esto, vale la pena pensar en un reloj de arena de muchos recipientes y aberturas distintas entre cada par: la arena tiende a concentrarse en los recipientes con abertura pequeña, equivalente a vida media larga; en cambio, en los de abertura grande, o vida media chica, pasan rápidamente al siguiente.

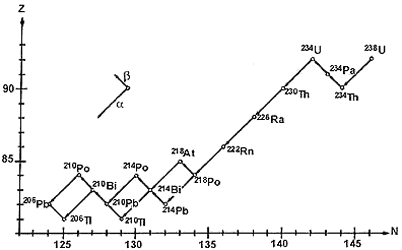
Figura 26. Cadena de decaimento del ²³⁸U.

Las diferentes vidas medias de los radioisótopos dan lugar a una serie de efectos, algunos útiles, otros nocivos. Por ejemplo, el que el uranio en la naturaleza tenga una vida media larga es causa de que constantemente estemos recibiendo radiación proveniente de él o de sus descendientes; pero, por otro lado, nos permite estimar la edad de la tierra. Un radioisótopo de vida media corta, el ¹³¹I (8.05 días) se puede usar para radiodiagnóstico inyectándolo al cuerpo, porque sus efectos desaparecen pronto.

Cuadro 6. Cadena de decaimento del ²³⁸U.

Elemento	Decaimiento	Vida media
238U	a	4.51 x 109 años
234Th	b	24.1 días
234Pa	b	1.18 minutos
234U	a	2.48 x 105 años
230Th	a	7.6 x 104años
226Ra	a	1.62 x 103años
222Rn	a	3.82 días
218Po	99.98 % a 0.02 % b	3.05 minutos
214Pb	b	26.8 minutos
218At	a	1.3 segundos
214Bi	99.96 % b 0.04 % a	19.7 minutos
214Po	a	1.6 x 10-4 segundos
210Tl	b	1.32 minutos
210Pb	b	22 años
210Bi	100 % b 0.0002 % a	5.0 días
210Po	a	138.4 días
206Tl	b	4.3 minutos
206Pb	estable

Ciertamente es el ¹⁴C el núcleo radiactivo que más se conoce como reloj nuclear, por dos razones principalmente: la primera, porque está presente en la materia orgánica; la segunda, porque su vida media de 5 730 años se presta para fechar objetos de interés arqueológico. Veamos cómo funciona. Recordemos (véase la Fig. 24) que si en un decaimiento exponencial se conoce la vida media y un punto de la curva, se puede calcular cualquier otro punto.

El ¹⁴C presente en la naturaleza tiene como origen la radiación cósmica, de donde provienen neutrones que, al bombardear nitrógeno, producen la siguiente reacción nuclear: ¹⁴N+n®¹⁴C+p. El ¹⁴C producido es radiactivo, por lo cual emite partículas b de baja energía. Como la radiación cósmica se mantiene más o menos constante se produce constantemente la misma cantidad de ¹⁴C, que se mezcla con los isótopos estables y se distribuye uniformemente en el bióxido de carbono del aire. Es recogido por las plantas y luego por los animales, hasta que en todos los seres vivos se tiene una fracción, pequeñísima pero bien definida, de ¹⁴C. En cuanto muere el organismo, deja de intercambiar carbono con el resto de los seres vivos y entonces el ¹⁴C que decae no se repone. En ese momento podemos decir que comienza a contar el reloj.

Tomemos un ejemplo hipotético. Una muestra de madera tomada de un entierro antiguo se pesa y se mide su actividad proveniente del ¹⁴C, encontrándose que esta actividad es exactamente la mitad de la de una muestra del mismo peso de madera cortada recientemente. Se deduce entonces que la edad de la muestra primera es 5 730 años, es decir, una vida media del ¹⁴C.

Si el razonamiento suena sencillo, el efectuar la medida no lo es. En primer lugar la energía de las partículas b que emite el ¹⁴C es muy pequeña, por lo que no es posible usar un contador convencional con ventana. Otra dificultad es que la cantidad de radiactividad que se debe medir es pequeñísima, difícilmente distinguible de la radiación ambiental, por lo que se deben usar sistemas especiales de conteo. Para vencer estos problemas, la muestra se transforma químicamente a forma líquida (benceno), para introducirla a un centellador líquido orgánico. Se requiere mucho cuidado en el manejo y la transformación de la muestra con la exactitud necesaria para no perder parte de ella. La mezcla luego se cuenta con un fotomultiplicador y se analizan los pulsos resultantes.

El método de datación usando ¹⁴C se empleó para uno de los descubrimientos más importantes de la arqueología de nuestro continente. Se trata de las excavaciones de la cueva de Coxcatlán en el Valle de Tehuacán, en donde se hallaron vestigios de maíz de diferentes antigñedades. Su fechado y la secuencia en que se encontraron demuestran claramente que ese pueblo sufrió un proceso evolutivo, de colectores primitivos de alimentos a comunidades agrícolas civilizadas, gradualmente entre 5 000 y 2,300 años a.C.

Para poder usar el método nuclear de calcular edades se necesita un sistema de reloj perfecto y que no entren ni salgan granos más que pasando por el orificio. Sí se escogen adecuadamente los isótopos es posible medir, por ejemplo, edades de rocas. Uno de los métodos que se usan es la combinación rubidio-estroncio. El ⁸⁷Rb existe en la naturaleza y decae a ⁸⁷Sr con una vida media de 4.7 X 10⁹ años. Esto significa que el estroncio normal de la naturaleza se va enriqueciendo lentamente en el isótopo 87 por el decaimiento del rubidio. Para aplicar este reloj nuclear a una muestra de un mineral dado se necesita: 1) mediante análisis químico saber cuánto rubidio tiene y medir su actividad b; 2) usando un espectrómetro de masas medir la abundancia de cada uno de los isótopos del estroncio (84, 86, 87 y 88) de la muestra y de una muestra de estroncio que no tenga rubidio; 3) la diferencia de la cantidad de ⁸⁷Sr en las dos muestras se puede atribuir al decaimiento del ⁸⁷Rb en el mineral, de donde se puede calcular su edad.

Otro método que se ha usado para medir edades geológicas es el de la fisión del uranio. El isótopo más abundante del uranio, el ²³⁸U, decae con emisión de partículas a, según ya vimos en la cadena de decaimiento. Pero hay otra manera en que puede decaer. Existe la posibilidad (muy remota, pero bien medida de que el ²³⁸U se fisione espontáneamente, o sea, se rompa en dos partes de masas no muy distintas una de la otra. La fisión del ²³⁵U, inducida por el bombardeo de neutrones, es la fuente de energía de los reactores nucleares de fisión; sin embargo, aquí estamos tratando con un fenómeno espontáneo. Solo, sin requerir de ningún estimulo extraño, el ²³⁸U puede fisionarse con una vida media de cerca de 0.8 X 10¹⁶ años. Como el uranio está presente en muchos lados en cantidades minúsculas esta fisión espontánea puede usarse también como reloj nuclear.

Resulta que al producirse la fisión los dos fragmentos salen despedidos con gran energía, como en una explosión. Aunque se trata sólo de núcleos aislados, su energía ocasiona que al pasar por la materia circundante la dañen fuertemente, dejando un trazo microscópico de daños que quedan impresos en el material. En ciertos materiales estos trazos pueden persistir durante millones de años, siempre y cuando el material no cambie de estado. Sí las regiones dañadas son atacadas con reactivos químicos, se vuelven visibles con un microscopio óptico normal. Uno puede entonces contar con trazos y deducir cuántas fisiones han sucedido, esto es, cuánto tiempo ha pasado. Para poder aplicar la curva de decaimiento se necesita conocer cuánto uranio hay en la muestra. Esto puede lograrse si se coloca dentro de un reactor nuclear, sometida a un flujo conocido de neutrones, con los que se induce la fisión en dos isótopos de uranio (235 y 238). Se vuelve a atacar químicamente para ver los trazos producidos, y de allí se deduce la cantidad total de uranio en la muestra. En obsidianas del campo geotérmico de la Primavera, en el Estado de Jalisco, se han observado trazas de productos de esta fisión espontánea. Su fechado ayuda en el análisis geológico para buscar campos con energía térmica que resulten económicamente rentables.

Estos métodos y otros semejantes (por ejemplo, el decaimiento de uranio en plomo) han dado la pauta para medir la edad de la Tierra. En la actualidad se acepta que es alrededor de 4.5 X l0⁹ años, o sea, 4 500 000 000 de años.

Hemos visto que muchos núcleos se desintegran con diferentes vidas medias. Ahora se antoja una pregunta fascinante: ¿los protones y neutrones que constituyen los núcleos pueden desintegrarse, y por lo tanto, podría esperarse que la materia como la conocemos se convirtiese en otra forma? La respuesta es la siguiente: de los neutrones, efectivamente sabemos que decaen en protón, electrón y neutrino con una vida media de 12 minutos (cuadro 5). Sin embargo, esto sólo puede suceder si los neutrones están libres; no sucede si están en un núcleo junto con otros protones y neutrones. Para el posible decaimiento del protón se han propuesto varios esquemas, de los que el más probable dice que el protón puede decaer en un pión neutro y un positrón. Sin embargo, este proceso nunca se ha observado naturalmente a pesar de que se han dedicado muchos esfuerzos a ello. No sólo no se ha observado, sino que se tiene 90% de certeza de que, si sucede, la vida media del decaimiento del protón seria.. ñmayor de l0³¹ años! Así que podemos estar tranquilos: en nuestro lapso de vida la materia no va a transformarse en otra cosa.