III. ELEMENTOS PARA EL AN�LISIS DE UNA IMAGEN DIGITAL.

Los elementos subjetivos del paisaje, como son vistos por un observador, son cuantificados por un barredor multiespectral automatizado y sientan, con el conjunto de datos resultantes, las bases para un an�lisis objetivo de la escena con fines de gesti�n racional del paisaje.

VEAMOS ahora los elementos b�sicos para el an�lisis de una imagen multiespectral digital. Se ha dicho anteriormente que una imagen digital es la representaci�n l�gica de una escena y que en general esta representaci�n tiene forma num�rica y algunas veces visual. Se ha analizado tambi�n la mec�nica de la captura y registro de una escena en forma de imagen digital, pero, �qu� significa f�sicamente en su forma m�s general una imagen multiespectral digital? Esto es importante para entender el mecanismo de an�lisis que se requiere para estudiar el funcionamiento de una escena. As� pues, puede decirse que es la variaci�n espacial y espectral de la "energ�a luminosa" proveniente de aqu�lla. Este concepto es igualmente v�lido cuando la escena emite o refleja part�culas como protones o neutrones o interacciona con se�ales ac�sticas, en cuyos casos la frase entre comillas deber� leerse "energ�a penetrante" o "energ�a ac�stica". Para entender esto hay que recordar que cuando un barredor multiespectral mide la energ�a luminosa, penetrante o ac�stica) proveniente de un determinado CIV, obtiene en forma simult�nea un conjunto de n�meros que dan en realidad el valor de la energ�a luminosa vista a trav�s de un conjunto de filtros de color, es decir que se observa la variaci�n de color a color para un mismo CIV. La energ�a "luminosa" se refiere a luz visible e invisible, como la infrarroja y la ultravioleta. Por su parte, aunque la energ�a penetrante, como la de un haz de protones, y la energ�a ac�stica son seleccionadas por otros m�todos diferentes a los filtros de color, siempre se podr� hablar, en t�rminos generales, de filtros para obtener una energ�a determinada. Como la percepci�n remota utiliza principalmente la energ�a "luminosa", se emplear� este t�rmino con frecuencia, en la inteligencia de que otros tipos de energ�a pueden ser tambi�n aprovechados por ella. Por tanto, podemos decir que para un mismo CIV el barredor multiespectral mide el cambio de color a color (o de energ�a), o bien la variaci�n espectral de la energ�a luminosa (penetrante o ac�stica) respectiva. Entendemos aqu� por variaci�n espectral al cambio de energ�a de la radiaci�n luminosa, penetrante o ac�stica. A partir de esto es f�cil comprender que de un CIV a otro la energ�a luminosa ser�, en general, diferente y que, por tanto, la imagen digital es la medida del cambio de dicha energ�a plasmada en el valor de un pixel a otro, lo que quiere decir finalmente que el conjunto de valores de los pixels de una imagen digital forman el cambio o variaci�n espacial de la energ�a proveniente de los CIV de la escena. Al desplazar un punto de un lugar a otro sobre una imagen digital, se encontrar�n diferentes valores (Figuras 13 y 16) de los pixels, y esta variaci�n espacial de la energ�a luminosa traer� como consecuencia una variaci�n espectral, ya que para cada pixel se tiene un juego de valores que son la variaci�n espectral del CIV correspondiente en la escena. Las variaciones espaciales y espectrales est�n tan estrechamente ligadas que el cambio de una implica la otra.

Ahora bien, al adquirir una serie de im�genes multiespectrales de una misma escena, pero en diferentes tiempos, se tendr� registrada una variaci�n temporal de las caracter�sticas de aqu�lla, lo que implica que las im�genes digitales correspondientes contendr�n simult�neamente las variaciones espacial y espectral de la energ�a proveniente de dicha escena a medida que �sta evoluciona en el tiempo. Para continuar con el estudio de los elementos b�sicos de una imagen digital con fines de an�lisis es necesario ahora introducir el concepto patr�n espacial y patr�n espectral. Un patr�n es esencialmente un arreglo de entes sin tomar en cuenta la naturaleza de �stos. Puede afirmarse, por otro lado, que el Universo est� formado por patrones. Por su parte, un ente es cualquier objeto f�sico o l�gico; un n�mero, una figura geom�trica o una ave son ejemplos de entes. Entonces, la sucesi�n de n�meros 4, 17, 19, 16, es un patr�n, diferente desde luego al patr�n 17, 4, 16, 19; queda claro en este ejemplo que lo que importa es el orden que guardan los n�meros entre s� y no si se trata de los mismos o no. El n�mero de entes en un patr�n puede ser cualquiera entre dos e infinito; as�, por ejemplo, la sucesi�n 4, 17, 16, 8 ser� un patr�n diferente al primero ejemplificado aqu�. La variedad de patrones es por tanto infinita, pues cualquier combinaci�n es posible. Es importante hacer notar tambi�n que el arreglo de los entes puede ser de naturaleza l�gica o f�sica; en los ejemplos que hemos mencionado se ha tratado del orden l�gico de los n�meros involucrados. Si los entes son f�sicos, entonces el orden ser� tambi�n de naturaleza f�sica, y por tanto �ste podr� darse a lo largo de un eje o sobre una superficie, como sucede en el caso del arreglo de objetos en una escena. Es muy importante tener presente que en la representaci�n num�rica de una imagen digital s�lo podemos hablar de patrones l�gicos, no as� en la representaci�n visual de la misma imagen, donde �stos tienen una equivalencia f�sica. Veamos ahora estos conceptos aplicados al caso de una imagen multiespectral digital (Figura 16). La sucesi�n de n�meros 42, 48, 59, 63, representa la variaci�n espectral del CIV correspondiente a este pixel en la imagen digital; a esta sucesi�n de valores sobre los diferentes planos que componen la imagen digital multiespectral se le llama patr�n espectral; dicho de otra manera un pixel representa un patr�n espectral. Por lo tanto, un patr�n de este tipo est� formado por la sucesi�n de valores que presenta un CIV determinado cuando es visto bajo diferentes filtros y, como hab�amos dicho anteriormente, esta sucesi�n es �nica para cada objeto de la naturaleza, de tal forma que dicho objeto tiene un patr�n espectral �nico. De ah� que se haya hecho costumbre llamarle firma espectral. (Figura 12.) Es claro que la firma espectral de un objeto cualquiera es un patr�n de tipo l�gico. En la figura 16 se ha dibujado tambi�n un conjunto de pixels con una cierta variedad de valores; si bien en esta simplificaci�n puede observarse con facilidad que aquellos que tienen valores alrededor del 60 forman una figura geom�trica irregular, el resto tienen valores notablemente m�s bajos y como tales se constituyen en una especie de fondo. El arreglo espacial de pixels con valores alrededor del 60 forman lo que se conoce precisamente como patr�n espacial. Es interesante hacer notar, como ya se apunt� arriba, que en este ejemplo se trata de entes de tipo l�gico pero con un orden f�sico, es decir, tienen una posici�n definida en el espacio. En una imagen multiespectral digital los patrones espectrales son siempre de tipo l�gico y los patrones espaciales son l�gicos en la representaci�n num�rica y f�sicos en la representaci�n visual. Desde luego, hay patrones espaciales formados por objetos f�sicos, como es el caso de un arreglo particular de aves cuando �stas vuelan en una parvada, puesto que resulta suficiente con que una ave cambie de posici�n relativa con respecto al resto para que el conjunto forme un nuevo patr�n. En forma intuitiva podemos decir tambi�n que desde el punto de vista f�sico existen patrones tanto espectrales como espaciales (Figura 21) que no difieren mucho entre s�. As�, por ejemplo, el patr�n espectral 4,17,19, 16 es muy similar al 4, 17, 19, 15, y probablemente se trate de dos objetos de la misma naturaleza f�sica, pero con peque�as diferencias. Entre patrones espaciales tambi�n puede haberlas: �nicamente mover de posici�n un solo pixel del patr�n espacial de la figura 17, se tendr� formalmente otro diferente, aunque �ste se parezca mucho al original.

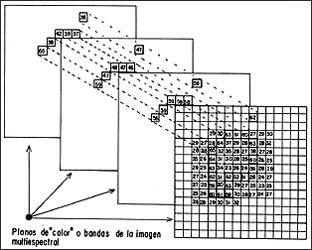
Figura 16. Patrones espacial y espectral de una imagen digital multiespectral.

Figura 17. En esta imagen de un sensor aerotransportado se observa un conjunto de patrones rectangulares que tienen caracter�sticas espectrales similares. Estos patrones rectangulares son los asociados a una serie de edificios.

En la operaci�n del barredor multiespectral, debido a variaciones de tipo estad�stico, pueden ocurrir peque�as fluctuaciones en los valores respectivos para el patr�n espectral, aun en el caso de objetos iguales que se encuentren colocados en diferentes posiciones de la escena. Algo similar puede suceder para patrones espaciales, en donde la naturaleza discreta de la imagen hace que algunos pixels queden ligeramente desplazados resultando peque�as diferencias en la imagen digital, aun cuando en la escena se trate de lo mismo. A estas fluctuaciones estad�sticas en el proceso de captura y registro de una imagen digital se suman en general otros factores que pueden llegar a ser muy importantes. Por ejemplo, en el caso de una imagen Landsat, la energ�a luminosa al viajar desde la superficie terrestre al barredor multiespectral atraviesa la atm�sfera, cuyas condiciones de visibilidad pueden ser diferentes de un lugar a otro de la escena, de tal manera que en la pr�ctica las condiciones de iluminaci�n para la escena no son homog�neas. En el caso de una radiograf�a del tejido �seo, los rayos X atraviesan el cuerpo humano, el cual presenta no s�lo diferencias en el espesor sino tambi�n diferentes condiciones del tejido blando, haciendo con esto que los huesos aparezcan en diferentes tonalidades de gris; a esto hay que agregar el hecho de que los huesos tampoco presentan condiciones de homogeneidad; as�, el tejido �seo se muestra con variaciones de densidad y espesor de un lugar a otro a lo largo del cuerpo humano. Todos estos factores hacen que, tanto los patrones espectrales como los espaciales de una imagen digital se vean formalmente diferentes, pero con caracter�sticas similares, y son precisamente estas caracter�sticas las que permiten la comparaci�n e identificaci�n de objetos semejantes en la escena. Podemos decir ahora, que una imagen digital multiespectral es una composici�n de patrones espectrales y patrones espaciales, y junto con la interrelaci�n que tienen �stos, es lo que constituye la estructura de una imagen digital multiespectral. Esta interrelaci�n se refiere a la relaci�n que tiene el valor de un pixel con sus vecinos, es decir, qu� tan r�pido var�a el valor de un pixel a otro, y es, por tanto, una medida de qu� tan r�pido se muestran visualmente las variaciones en tonos de gris o de color en la representaci�n visual de una imagen digital. De hecho existe un n�mero tan grande de posibles interrelaciones entre patrones, que no hay manera de describir en forma exhaustiva la variedad de estructuras que pueden resultar en una imagen digital de regular tama�o, digamos de 1 024 x 1 024 pixels. Para ilustrar esto supongamos que, como en un juego gigantesco de rompecabezas, tenemos 1 024 x 1 024 (1 048 546) juegos de cuadros de 128 posibles tonos de gris, con lo que entonces podemos formar m�s de un mill�n de im�genes con 128 niveles de gris, muchas de las cuales presentar�n formas familiares a nuestra vida diaria. Si tenemos muchos millones de peque�os cuadrados con 128 posibles tonalidades, entonces podremos formar m�s im�genes de por ejemplo 1 024 x 1 024 pixels, pudiendo componer con esto casi cualquier figura que conozcamos en la vida cotidiana. Por otro lado, es posible dar suficientes ejemplos para esclarecer este tan importante concepto de estructura de una imagen digital, como introducir los elementos b�sicos con los cuales descomponer una imagen para facilitar no nada m�s su comprensi�n, sino tambi�n su an�lisis. Para esto partamos de un ejemplo extremadamente sencillo: supongamos que tenemos una imagen digital multiespectral cuyos pixels son del mismo valor o tono, es decir, la imagen aparece homog�nea a la vista. �Qu� tipo de interrelaci�n guardan en esta imagen los patrones espectrales y espaciales? Pues bien, todos los patrones espectrales tendr�n el mismo juego de valores num�ricos a lo largo de los diferentes planos de color: por ejemplo, 7, 13, 17, 21 y 22, para una imagen multiespectral formada por cinco bandas. La relaci�n de pixel a pixel ser� muy simple: uno; cualquier pixel ser� igual a sus vecinos. Veamos ahora un ejemplo un poco m�s complejo: consideremos una imagen como la de la figura 16. En este caso existen fluctuaciones relativamente peque�as entre los patrones espectrales, tanto para los pixels que forman la figura geom�trica, como para el resto de la imagen o fondo. La relaci�n de un pixel con sus vecinos no es tan alta como en el caso anterior, pero s� es cercana al 100%: casi igual a uno. En otras palabras, ya sea para la figura geom�trica o para el fondo, las fluctuaciones de pixel a pixel son relativamente peque�as, entre el fondo y la figura geom�trica la relaci�n de los valores de los pixels es de aproximadamente 1/2, lo que implica que hay un cambio brusco del fondo a la figura geom�trica. Desde luego, esto significa que la relaci�n de los pixels que forman la figura geom�trica con sus vecinos (los del fondo) es realmente baja: aqu� el cambio de un pixel a otro es bastante brusco, pues esto es precisamente lo que define en forma clara la mencionada figura, o visto desde otra perspectiva, los pixels que forman el fondo tienen poco que ver con aqu�llos que forman la figura geom�trica. De aqu� podemos plantear que, en el primer ejemplo, donde consideramos una imagen homog�nea, la estructura es la m�s simple que puede existir, y en el segundo (Figura 16), que la estructura es algo m�s compleja, esto es que es de tipo binario: s�lo existen dos patrones espaciales o dos grupos de patrones espectrales. Analicemos ahora im�genes con estructuras m�s complejas y para esto vayamos a la figura 10, en la que vemos en tonos de gris y con variaciones suaves el rostro de una mujer: �c�mo podemos afirmar que diferenciamos el patr�n espacial "ojos, boca o nariz"? En estos casos un mismo patr�n espacial no presenta fronteras tan definidas ni un nivel de valores tan homog�neos como aquellos patrones de la figura 16. Por tanto, en primer lugar podemos afirmar que los mencionados patrones del rostro de la mujer se encuentran embebidos en un contexto que es precisamente el rostro, y en segundo, que el cerebro humano es capaz de suplir aquellas partes faltantes o poco claras del patr�n en cuesti�n. Esto quiere decir que distinguir dichos patrones est� �ntimamente relacionado con un proceso cerebral que a�n no se encuentra claramente entendido; en otras palabras, la determinaci�n o no de un patr�n espacial no se debe nada m�s a su existencia f�sica, sino tambi�n al proceso o m�todo de an�lisis de la imagen y, como el proceso cerebral mencionado no se encuentra completamente clarificado, podemos afirmar que el reconocimiento o no de un patr�n espacial puede finalmente constituirse como un hecho subjetivo y, como tal, depende del observador, del barredor multiespectral, de las condiciones de iluminaci�n de la escena, del tama�o del CIV en relaci�n con �sta y del m�todo de an�lisis. No puede obviarse esta subjetividad diciendo que un patr�n espacial podr� reconocerse autom�ticamente por medio de una computadora, puesto que los algoritmos computacionales para hacer dicho reconocimiento los tiene que escribir un ser humano, que es quien va a plasmar en tales algoritmos criterios de car�cter subjetivo. �Qu� podemos decir entonces acerca de estructuras m�s complejas? Podemos afirmar tres cosas: 1) siempre habr� en una imagen digital patrones espaciales bien definidos tanto en su forma y su frontera, como en la extensi�n que ocupan, los que podr�n distinguirse sin ambig�edad ya sea por cualquier observador, o por una computadora debidamente programada; 2) ciertos patrones aparecer�n como aqu�llos de la figura 10, en donde es necesario el manejo de elementos subjetivos para identificar los patrones espaciales sin ambig�edad; claramente ser� indispensable introducir, debido a tal subjetividad, un conjunto de reglas que unifiquen en forma arbitraria, pero pr�ctica, dichos elementos y 3) un conjunto relativamente peque�o de patrones para los que no es posible un an�lisis sin caer necesariamente en ambig�edades, de tal forma que el reconocimiento de esta clase de patrones es realmente circunstancial; para este tipo de patrones se requiere por tanto de una unificaci�n de criterios y condiciones bajo las cuales se debe capturar la imagen digital correspondiente a la escena que se desee analizar. Por ejemplo, ciertas condiciones de iluminaci�n pueden hacer aparecer a una imagen con sombras pronunciadas impidiendo la definici�n clara de varios patrones espaciales.

Puede afirmarse ahora que los patrones espectrales siendo l�gicos y por tanto bien definidos no presentan finalmente ning�n grado de subjetividad, puesto que �sta ha sido ya previamente clarificada a trav�s de axiomas y definiciones concernientes al sistema de n�meros naturales. De ah� que el patr�n espectral 4, 17, 19, 16 sea clara y definitivamente diferente a cualquier otra combinaci�n de cuatro n�meros naturales y por tanto est� constituido en un patr�n espectral �nico. Ahora bien, como ya hab�amos comenzado a estudiar en el p�rrafo anterior, la situaci�n para los patrones espaciales no es tan sencilla cuando se trata de im�genes con estructuras relativamente complejas. En relaci�n a esto hab�amos mencionado que existen tres grados o clases de patrones de esta clase de acuerdo a la objetividad o subjetividad involucrada en su reconocimiento y que los tres pod�an estar presentes en una imagen digital, lo que tra�a como consecuencia que la interrelaci�n entre un patr�n espacial y el resto de la imagen, o bien entre un patr�n y otros, ya no sea tan sencilla como el que tiene el patr�n geom�trico de la figura 16 con el resto de la imagen. En casos m�s complejos, la interrelaci�n es variable de un pixel a otro y de un patr�n espacial a otro, como sucede por ejemplo en una radiograf�a, en donde tanto una costilla va cambiando de tono de un lugar a otro, como la relaci�n entre un pixel-costilla y un pixel-tejido blando. En la pr�ctica, esta variedad en los patrones espaciales hace que se impongan necesariamente reglas en el proceso de captura y registro de im�genes, reglas tales que garanticen la uniformidad en las caracter�sticas de una clase de patrones, al menos para un conjunto específico de ellas como lo pueden ser las radiograf�as o las im�genes satelitarias. Supongamos ahora que se han ya uniformizado los criterios para un cierto conjunto de im�genes multiespectrales y que se han establecido reglas para evitar al m�ximo la ambig�edad. Hecho esto podemos plantear f�cilmente que la estructura de una imagen multiespectral est� dada por el conjunto de patrones espectrales y espaciales que la componen y por la interrelaci�n que guardan entre ellos, siendo esta interrelaci�n la raz�n de valores num�ricos que un determinado pixel guarda con todos sus vecinos en cada una de las bandas de la imagen. En una imagen como �sta dicha raz�n ser� diferente de un plano de la imagen a otro, aun cuando se trate del mismo pixel. As�, por ejemplo, suponiendo dos pixels contiguos cuyos valores a trav�s de los diferentes planos de color de una imagen multiespectral forman los patrones espectrales 4, 17, 19, 16 y 8, 15, 13, 10, tendr�n la raz�n de valor 1/2 para el primer plano, pero una raz�n diferente para los planos segundo, tercero y cuarto respectivamente 17/15, 19/13 y 8/5. La interrelaci�n de los pixels que componen un patr�n espacial con los pixels vecinos es muy importante, puesto que si la raz�n es cercana a uno, el patr�n dif�cilmente podr� distinguirse, mientras que si la raz�n es diferente de uno, tendr� un contraste mayor con respecto al resto de la imagen y ser� f�cil identificarlo. Es necesario decir que dado que dicha raz�n cambia de plano a plano, es posible que un patr�n sea identificable en un plano pero no en otro. Hay que puntualizar aqu�, que s�lo es importante para la diferenciaci�n de un patr�n espacial, la raz�n de los pixels que lo componen con los pixels vecinos pr�ximos; no tiene sentido hablar de la raz�n de tales pixels con vecinos alejados, puesto que �stos no contribuyen al contraste del patr�n espacial en cuesti�n.

Otra manera de ver a un patr�n de este tipo es a trav�s del concepto de estructura, es decir considerando a un patr�n espacial como una estructura elemental que forma parte de una imagen o estructura compleja. Por tanto, una imagen digital multiespectral podr� ser vista como la superposici�n de estructuras elementales o semielementales cuya forma y tama�o se mantiene, en principio, de plano a plano de color, pero cuya interrelaci�n cambia en forma dependiente a la variaci�n espacial de los valores de los pixels que componen dicha estructura. Esto significa que un plano de color determinado conteniendo una estructura elemental podr� tener buen contraste, pero que, en otro plano, �ste ser� de tal magnitud que, o aparecer� en forma tenue, o tal vez ni siquiera pueda distinguirse. De hecho no existe un juego b�sico de estructuras elementales; la variedad de patrones espaciales es tal que hace imposible la definici�n de dicho juego. M�s bien lo que se establece es un conjunto caracter�stico o t�pico de estructuras elementales con relaci�n a una aplicaci�n espec�fica, con lo que, por ejemplo, trat�ndose del problema de la forma de un determinado virus, no se manejar�n todas las formas posibles que �ste adopta a lo largo de su existencia, sino m�s bien un subconjunto suficiente para determinar, digamos, la forma que adquiere cuando se encuentra en un claro estado de virulencia. En resumen, establecer un conjunto de estructuras elementales se hace por medio de una decisi�n arbitraria, pero con sentido pr�ctico; en la suposici�n, claro est�, de que los criterios para la identificaci�n un�voca de tales estructuras han sido ya seleccionados y cuantificados. En una imagen de la superficie terrestre tomada desde un sat�lite, los diferentes patrones de drenaje del agua que escurre hacia las partes bajas podr�an ser consideradas como estructuras elementales. Tambi�n lo ser�n las formas de las cadenas monta�osas cuya forma y tama�o son relevantes en la exploraci�n geol�gica. Los diferentes tipos de cobertura vegetal pueden ser tambi�n consideradas como patrones espaciales elementales; �stos, combinados con informaci�n a la cual se encuentran localizadas las diferentes especies vegetales, forman elementos de considerable importancia en el estudio de la superficie terrestre y los recursos naturales. De hecho, cuando el hombre observa con la vista al medio que le rodea, establece de inmediato un conjunto b�sico de patrones o estructuras elementales, lo que hace en forma arbitraria, pero con sentido pr�ctico, dependiendo del contexto en que se encuentre; as�, por ejemplo, un transe�nte en la calle definir� a los autom�viles como estructuras elementales, pero un mec�nico en su taller ver� el autom�vil como una estructura compleja y a las diferentes partes del motor y la carrocer�a las ver� como estructuras elementales. A manera de recapitulaci�n de estas ideas podemos decir que una imagen digital multiespectral est� formada en su totalidad por un conjunto de patrones espaciales complejos, tantos patrones como planos de color haya, y que cada plano es, a su vez, el resultado de la interrelaci�n de estructuras espaciales semielementales o cuasielementales, definidas �stas de acuerdo al contexto en el cual se desea analizar dicha imagen.

Ahora bien, por medio de la visi�n y del sentido del tacto un ser humano es capaz de distinguir en forma intuitiva diversos tipos de textura. En una muestra de diferentes telas, se puede establecer una clasificaci�n cualitativa, desde las m�s rugosas hasta las m�s lisas. �Cu�les son los criterios que se utilizan en esta clasificaci�n? Una tela completamente lisa es aqu�lla que no presenta ninguna variaci�n del relieve a la hora de deslizar los dedos por su superficie; esto quiere decir que si vi�ramos a la tela de perfil, la ver�amos completamente plana, como la superficie de un vidrio; en cambio, una tela rugosa presentar� variaciones abruptas en todas las direcciones, y de perfil se ver� una l�nea accidentada. Sin embargo, la textura no puede entenderse �nicamente como un cierto grado de rugosidad, en ella tambi�n interviene el tipo de variaci�n de tal rugosidad y en qu� direcci�n o direcciones se presenta �sta. De esta manera, una sucesi�n lineal de crestas y valles no ser� lo mismo que un cuadriculado de crestas y valles; el n�mero de posibles combinaciones para dichas variaciones es pr�cticamente ilimitado. Puede decirse entonces que el patr�n espacial que presenta la rugosidad en una tela es lo que determina la textura de la misma, o en otras palabras, la rugosidad de una tela se presenta a la vista como una sucesi�n de tonos que forman un patr�n espacial y esta sucesi�n tiene una correlaci�n estrecha con la rugosidad perceptible al tacto. �Qu� puede decirse ahora en cuanto a la textura de una imagen digital? En una imagen continua no podemos hablar directamente de rugosidad, s�lo podemos hacerlo de cambios de tono de color a medida que uno se desplaza de un punto a otro de la imagen. Sin embargo, en una imagen digital podemos imaginar cuantitativamente que aquellos pixels que tienen un valor alto forman un pico o cresta y que los que tienen un valor bajo forman un valle o sima, de tal manera que puede establecerse una analog�a clara entre la rugosidad de una tela y esta "rugosidad" imaginaria de la imagen digital. Recordemos ahora que una imagen de este tipo tiene una representaci�n visual, y que los pixels de valor alto se traducen en tonos claros y los de valor bajo en tonos oscuros, de aqu� que finalmente las variaciones espaciales en tono o color de una imagen digital pueden entenderse como un cierto grado de "rugosidad" o textura. Veamos ahora algunos ejemplos para ahondar en estos conceptos de tipo intuitivo y dif�ciles de cuantificar.

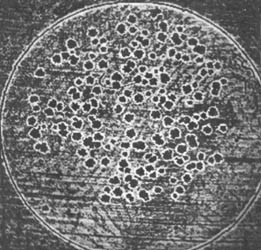
Figura 18. Imagen obtenida de un detector pl�stico donde se observa una serie de patrones circulares que corresponden a part�culas a.

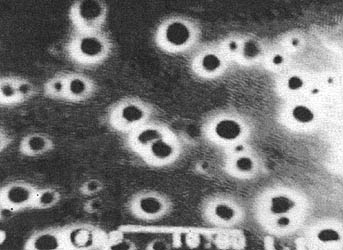
Figura 19. Los patrones circulares de esta imagen corresponden a las trazas de part�culas vistas a trav�s de un microscopio electr�nico.

Comencemos por las im�genes mostradas en las figuras 18 y 19 que presentan estructuras o patrones espaciales relativamente sencillos. En ambas figuras se pueden apreciar una serie de patrones circulares oscuros rodeados de un halo bastante claro; de acuerdo a los conceptos que acabamos de desarrollar podemos decir que tanto los patrones circulares como los halos tiene la misma textura y con esto queda asentado algo muy importante: la textura es independiente del tono o color de la imagen, ya que en este ejemplo la variaci�n espacial de los tonos de gris es la misma aunque en un caso sea clara y en el otro oscura. En la figura 18 se puede ver una sucesi�n de l�neas algo oscuras aproximadamente paralelas y separadas entre s� por zonas un poco m�s claras. Las regiones que contienen estas l�neas ser�n catalogadas como una clase de textura aparte; tambi�n ser�n clasificadas de esta manera aqu�llas que tienen una especie de "moteado", en donde se alternan, en forma aproximadamente regular y en todas direcciones, una sucesi�n de pixels oscuros y grises. En la figura 18, por tanto, diremos que hay tres clases de textura y, siguiendo razonamientos similares, lo mismo podr�amos decir de la figura 19. Algo un poco diferente se tiene en la figura 20; en ella se ven, en una especie de cuadriculado, una serie de patrones espaciales, donde cada cuadrado tiene estructuras rayadas y "moteadas" adem�s de que se pueden apreciar tambi�n algunas zonas muy claras, de las cuales se podr�a plantear que tienen una textura "lisa". No obstante estas clasificaciones intuitivas, resta algo de subjetividad en el concepto de textura, puesto que el cuadriculado de la figura 20 que contiene a las otras clases de textura, puede ser una clase de por s�; de aqu� que este concepto dependa siempre del contexto bajo el cual se le mire. Aun as� podemos decir que existen tres elementos objetivos en el concepto de textura, y es que �sta depende de: 1) la frecuencia de cambio de los tonos en los pixels; 2) de la direcci�n o direcciones de cambio, y 3) del contraste entre un pixel y sus vecinos.

>

Figura 20. Zona de cultivos en el valle del Yaqui, Sonora, captada por el sat�lite Landsat 2.

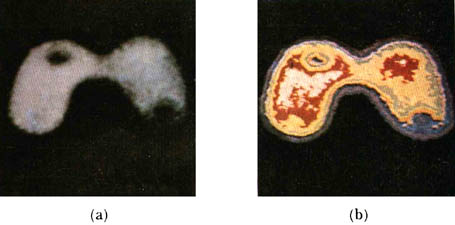
Figura 3. Imagen de la gl�ndula tiroides obtenida con un detector de rayos gamma. La parte superior es una representaci�n de dicha gl�ndula en tonos de grises y en la parte inferior se aprecia la misma en colores; es evidente que la representaci�n a color es mucho mejor.

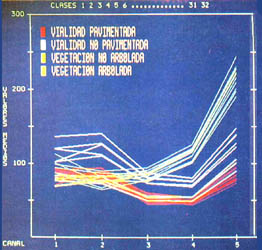
Figura 12. Muestra de cuatro "firmas espectrales" extra�das de los valores asociados a diferentes rasgos de la imagen de la ciudad de M�xico, obtenida por un sensor aerotransportado.

Figura 14. Imagen del sat�lite Landsat (TM) del �rea donde est� localizado el reactor nuclear de Chernobyl (ver flecha). La imagen fue tomada el 29 de abril de 1986, a las 18:52 hora local). La regi�n central de la imagen que aparece en negro es el estanque de enfriamiento asociado a la operaci�n del reactor.

Figura 26(a). En la parte inferior de esta imagen del Valle del Yaqui, Sonora, se aprecia una delgada nube que impide ver con claridad los cultivos y los canales de riego.

Figura 26(b). En esta imagen, la nube ha sido filtrada, habi�ndose recobrado buena parte de la informaci�n que estaba cubierta por la nube.

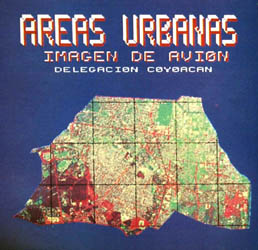
Figura 28(b). Este es el tipo de productos que se puede ofrecer la percepci�n remota en la cartograf�a de una ciudad como M�xico. En los diferentes colores se ven las comunicaciones viales, las zonas urbanas y las zonas arboladas.

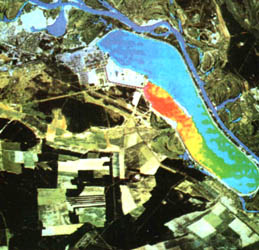
Figura 29(a). En esta toma del reactor de Chernobyl, antes de su explosi�n, se aprecia en rojo la descarga de aguas calientes producto de la operaci�n del reactor. En amarillo, verde y azul se observan las aguas gradualmente m�s fr�as, con lo que queda clara la distribuci�n particular de temperaturas del estanque de enfriamiento.

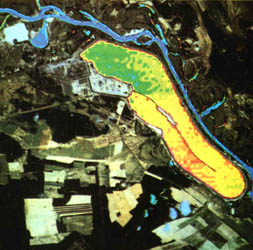
Figura 29(b). Despu�s del accidente en el reactor nuclear, la distribuci�n de temperaturas del estanque es m�s uniforme, lo que indica que el reactor ha cesado de operar puesto que ya no hay descarga de aguas calientes.

Figura 30. La apariencia rojiza de la cobertura vegetal de esta imagen se debe a que se utiliz� un filtro infrarrojo y esto permite evaluar con facilidad el estado de la vegetaci�n.

Pasemos ahora a estudiar otro elemento b�sico para el an�lisis de una imagen digital: la noci�n de forma de un patr�n espacial. El concepto de forma tiene m�s aspectos objetivos que el concepto de textura, ya que todos entendemos la diferencia entre un tri�ngulo y un cuadrado debido a que estas figuras tienen propiedades geom�tricas bien definidas que nos permiten determinar sus diferentes formas en una imagen digital, cuando se trata de figuras geom�tricas regulares e irregulares es posible distinguir una forma de otra, puesto que una figura geom�trica siempre puede verse como un pol�gono con �ngulos interiores y lados claramente definidos. Cabe aclarar que la naturaleza discreta de una imagen digital hace imposible que puedan considerarse l�neas continuas para figuras geom�tricas; �stas estar�n siempre representadas por l�neas quebradas o pol�gonos. Esto puede verse claramente al referirnos a la figura 21, en donde, por simplicidad en la discusi�n, se ha representado una figura binaria (s�lo dos valores de pixels) y en donde los unos representan el contorno de una figura geom�trica cualquiera. Consideramos tambi�n el diagrama de ocho posibles direcciones que pueden presentarse en una imagen digital y que se conoce como c�digo de Freeman. Por medio de este c�digo y comenzando por cualquier pixel de la figura geom�trica, digamos el de la extrema derecha, podemos asociar una cadena de n�meros a dicha figura. El proceso de asociaci�n es como sigue: el pixel remarcado en la figura 21 es el que se toma como punto de partida.

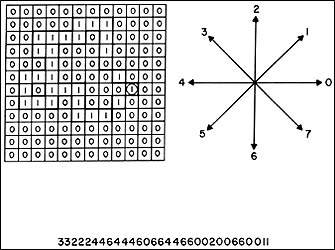
Figura 21. Patr�n espacial y su correspondiente representaci�n num�rica por medio del c�digo de Freeman.

Se inicia un recorrido hacia arriba en sentido contrario a las manecillas del reloj y se va asignando un n�mero seg�n el c�digo de Freeman; de esta manera, al siguiente pixel se le asigna el n�mero tres, ya que se encuentra en la direcci�n tres del mencionado c�digo. El pixel que sigue se halla en la misma direcci�n y por tanto se le otorga tambi�n el n�mero tres; el siguiente se encuentra hacia arriba, por lo que se le asigna el n�mero dos. El proceso se contin�a hasta recorrer completamente los pixels que componen la figura geom�trica; en este caso la cadena asignada resultante se muestra en la figura 21. Con esta cadena de n�meros o c�digo de Freeman hemos logrado un resultado muy importante, puesto que en ella se encuentra la informaci�n cuantitativa acerca de la forma de la figura geom�trica; haber planteado las cosas as� permite objetivar el concepto de forma aun para pol�gonos irregulares. Analicemos ahora con m�s detalle esta cadena de n�meros para verificar que esta representaci�n num�rica de la forma es realmente �nica para el ejemplo planteado y que no existen ambig�edades en el esquema planteado. En primer lugar, esta cadena de n�meros constituye un patr�n espacial (recu�rdese que un patr�n es un arreglo de entes de la misma naturaleza l�gica, que se refiere al espacio f�sico), puesto que recorrimos la figura geom�trica de pixel a pixel, es decir de un punto a otro en la representaci�n visual de la imagen digital. �Qu� sucede si la cadena la construimos a partir de otro pixel, digamos el que se encuentra en el extremo superior derecho de la figura geom�trica? Con la convenci�n de hacer el recorrido en el sentido contrario a las manecillas del reloj, se obtiene la siguiente cadena: 44644460664466002006600113322. �Acaso es esta cadena esencialmente la misma que la anterior? �se trata del mismo patr�n? Hablando superficialmente y en el contexto en el cual definimos a un patr�n la respuesta parecer�a ser no. Sin embargo, estamos considerando un patr�n espacial y por tanto tenemos que pensar en la posici�n relativa que guarda cada pixel de la figura geom�trica; adem�s, no olvidemos que la cadena obtenida representa un patr�n espacial y no un patr�n l�gico, en el cual el cambio de un solo ente implica un patr�n realmente diferente. Con estas consideraciones pasemos ahora a comparar las dos cadenas y para ello iniciemos el siguiente proceso de rotaci�n: comenzando con el n�mero de la extrema derecha de la �ltima cadena, pas�mosla al principio de la misma, a la izquierda de �sta, y comparemos n�mero a n�mero las dos cadenas; as� continuamos pasando n�mero a n�mero los elementos de la segunda cadena y compar�ndolas entre s� cada vez, es claro que despu�s de haber pasado a la izquierda los n�meros 33222, las dos cadenas ser�n exactamente iguales. En este momento podemos decir que si dos cadenas de dos figuras se comparan id�nticamente una vez durante una rotaci�n completa de los n�meros de cualquiera de las dos, entonces las dos figuras tienen la misma forma, es decir constituyen el mismo patr�n espacial, ya que los pixels guardan la misma posici�n relativa, aun cuando se rote la figura. En otras palabras, esta conceptualizaci�n de las formas para las figuras geom�tricas hace tambi�n que la representaci�n respectiva, por medio de las mencionadas cadenas, sea independiente de la orientaci�n de la figura, puesto que al girar la Figura 21, se obtiene una cadena igual a la que corresponde a la figura no girada, por supuesto, una vez hechas las rotaciones necesarias en cualquiera de ellas. El �ltimo problema que tenemos que resolver es el relativo al tama�o de las figuras geom�tricas que se consideren, ya que intuitivamente sabemos que la forma de una figura es independiente de las dimensiones de �sta; este concepto queda completamente clarificado cuando se amplifica el negativo de una fotograf�a a diferentes escalas: obviamente las formas de las figuras presentes en la foto ser�n las mismas independientemente del tama�o de las impresiones correspondientes. Para estudiar este �ltimo problema supongamos que tenemos dos rect�ngulos conc�ntricos (5 x 4 y 7 x 6 pixels), con lo que aseguramos que sean de la misma forma pero de tama�o diferente; entonces, siguiendo el c�digo de Freeman, las cadenas correspondientes ser�n: 00002224444666 y 0000002222244444466666, que se obtiene comenzando con el pixel del extremo izquierdo inferior y recorriendo los rect�ngulos en sentido contrario a las manecillas del reloj. Las cadenas as� obtenidas lucen similares, mas no iguales; si hici�ramos una comparaci�n como la planteada m�s arriba, concluir�amos err�neamente que las figuras consideradas tienen formas diferentes. Sin embargo pueden observarse que estas dos cadenas tienen estructuras semejantes: los d�gitos 0, 2, 4, 6 que intervienen en ambas guardan una relaci�n de proporci�n en cuanto al n�mero de veces que aparecen en cada cadena. Esto es as� debido a que al aumentar de tama�o el rect�ngulo se requieren de m�s pixels para representar cada lado y en consecuencia la cadena que caracteriza la forma correspondiente ser� proporcionalmente m�s grande. Es necesario aclarar que a diferencia de las posibles orientaciones que puede tener una figura donde los patrones espaciales correspondientes son los mismos, en el presente caso, donde los patrones respectivos son verdaderamente diferentes, �stos resultan ser semejantes gracias a que est�n relacionados a formas iguales. Lo que hemos hecho finalmente es introducir una conceptualizaci�n l�gica que nos permite comparar dos formas de manera cuantitativa. En resumen, podemos decir que una cadena de n�meros, producto de aplicar el c�digo de Freeman a un pol�gono cualquiera en una imagen digital, representa de manera adecuada y cuantitativa la forma asociada a dicho pol�gono, de tal manera que esta representaci�n es independiente de la orientaci�n y tama�o que pudiera tener dicho pol�gono. As� pues para comparar una forma con otra ser� necesario analizar la proporci�n de los d�gitos que aparecen en las cadenas respectivas, efectuar todas las rotaciones requeridas y comparar d�gito a d�gito las dos cadenas: las formas ser�n iguales, si aqu�llas son semejantes, y ser�n progresivamente diferentes a medida que difieran d�gito a d�gito. Cabe anotar aqu� que aunque l�gicamente se ve sencillo comparar dos formas o clasificarlas de acuerdo a un patr�n de formas, la tarea computacional se vuelve sumamente dif�cil, pues la implantaci�n de los algoritmos correspondientes a las rotaciones, proporciones y comparaciones no es directa ni obvia. Lo importante, sin embargo, es que en principio podemos cuantificar el concepto de forma y que �ste resulta ser un elemento de extrema importancia en el an�lisis de im�genes digitales.

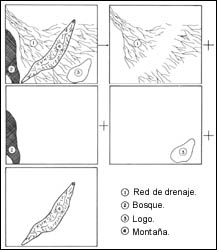
Figura 22. Banda de una imagen multiespectral sintetizada en un conjunto de estructuras quasielementales.

Imaginemos ahora que tomamos un plano cualquiera de una imagen multiespectral en la cual se encuentra una estructura espacial relativamente compleja. Pensemos tambi�n que hemos logrado conceptualizar esta estructura de tal manera que es posible sintetizarla por medio de un conjunto de estructuras quasielementos (figura 22). En el plano original se muestra una imagen donde est�n representados una monta�a, un bosque, un lago y una red de drenaje por donde fluye el agua que escurre desde la monta�a. En la sucesi�n de im�genes mostradas en la figura 22, aparecen cada uno de estos patrones espaciales o estructuras quasielementales. Como se hab�a dicho anteriormente, en la pr�ctica estos patrones pueden no aparecer ni tan claros ni tan bien definidos como se muestran en la figura. La s�ntesis mencionada consiste b�sicamente en que cada estructura quasielemental ha sido aislada o separada del resto de la imagen original y puesta en una imagen aparte; a este proceso se le llama segmentaci�n de la imagen digital. En otras palabras, la segmentaci�n es la representaci�n de una estructura compleja por medio de un conjunto de estructuras quasielementales. Cabe preguntar aqu�: �cu�l es el objeto de segmentar una imagen digital? Aparte de conceptualizar una estructura compleja en sus partes, lo cual es muy �til puesto que el desglose de cualquier objeto en sus componentes b�sicos es un m�todo de estudio bien establecido, se tienen otras consecuencias importantes en el an�lisis de una imagen digital. Al separar cada objeto estamos en posibilidades de evaluarlo en forma automatizada sin tener complicaciones innecesarias en la ejecuci�n de algoritmos computacionales; al evaluar la forma del bosque, la monta�a o el lago, lo hacemos por separado sin tener que escribir un programa de computadora que "reconozca" que se trata de tres objetos diferentes. Adem�s de que si bien para fines cuantitativos la forma de un bosque puede ser la misma que la de un lago, no es as� para las consecuencias que trae una forma determinada en el �rea de la silvicultura o en el de la geohidrolog�a, respectivamente. Por otro lado, es muy posible que se desee o se requiera aplicar diferentes criterios de an�lisis a diferentes estructuras: as�, por ejemplo, ser� necesario determinar el �rea boscosa y la superficie cubierta por el lago, pero para el caso de la monta�a ser� m�s importante determinar su forma y para la red hidrol�gica el n�mero de cauces por unidad de superficie que permita obtener el flujo de agua hacia las partes bajas. Podemos ahora decir que la segmentaci�n de una imagen no es nada m�s un recurso l�gico para conceptualizar una estructura compleja, sino tambi�n un recurso para simplificar el an�lisis computacional de las propiedades geom�tricas de las estructuras quasielementales. Las propiedades geom�tricas de un patr�n espacial, tales como forma, per�metro, �rea cubierta y textura, son las que constituyen la morfolog�a de tal patr�n, y su determinaci�n es necesaria en la soluci�n de problemas espec�ficos. La morfolog�a de un tumor, por ejemplo, puede ser indicativa del tipo de tejido y de la malignidad correspondiente, y la morfolog�a de una cadena monta�osa puede dar indicios sobre la historia geol�gica de una regi�n determinada. No es necesario que la segmentaci�n se realice en forma f�sica; en muchos casos es suficiente una separaci�n l�gica, en donde a cada estructura quasielemental se le asigne un plano virtual; esto es, s�lo existe una representaci�n num�rica de las estructuras y a esta representaci�n se le asigna un c�digo diferente que simboliza un plano virtual determinado.

Un patr�n espacial en una imagen digital multiespectral es en realidad un conjunto de patrones espectrales con caracter�sticas similares. Para clarificar esto y estudiarlo con mayor detalle regresemos a la figura 16, la cual muestra un patr�n espacial simple que bien podr�a catalogarse como una estructura quasielemental. A lo largo de este patr�n, las caracter�sticas de los patrones espectrales son aproximadamente las mismas, por lo que los juegos de n�meros que los representan son muy parecidos entre s� a trav�s de los planos de color de la imagen multiespectral. En la figura 16 se han representado cuatro patrones espectrales, contiguos entre s�, que forman parte del patr�n espacial; estos juegos de n�meros son, yendo de izquierda a derecha sobre la imagen digital, los siguientes: (64, 59, 47, 38), (63, 59, 48, 42), (61, 58, 47, 39) y (60, 58, 46, 37). Es claro que podemos esperar juegos parecidos para el resto de los patrones espectrales que conforman al patr�n espacial mostrado en la figura 16. Con todo existen peque�as diferencias entre estos patrones que podr�amos atribuir a variaciones provenientes del sensor remoto o a cambios ligeros del objeto correspondiente en la escena. Estas peque�as diferencias se muestran como fluctuaciones estad�sticas de rango peque�o que no afectan en la separabilidad (en este ejemplo) del patr�n espacial del resto de la imagen. Desde luego, existen criterios de tipo estad�stico que nos permiten en forma cuantitativa determinar cu�ndo un patr�n espacial tiene fluctuaciones de rango peque�o y cu�ndo no, o bien establecer cu�ndo un patr�n espectral pertenece o no a un patr�n espacial. En forma intuitiva podemos afirmar que el patr�n espectral (62, 58, 47, 38), que se encuentra un poco arriba de la forma geom�trica mostrada en la figura 16, tiene caracter�sticas parecidas a los patrones espectrales que forman dicha figura geom�trica o patr�n espacial. De tal manera, puede decirse que este �ltimo patr�n espacial pertenece tambi�n a la figura geom�trica, con lo que es evidente que un patr�n espacial puede ser tan complejo como se quiera, adem�s de que nos demuestra que los pixels de un patr�n espacial determinado pueden estar en diversas partes de la imagen digital, sin ser necesario que sean vecinos pr�ximos. M�s a�n, un patr�n de este tipo puede estar formado por un conjunto de pixels vecinos entre s� y cubriendo una �rea determinada como sucede en el caso de la zona boscosa y el lago de la figura 22, o mostrarse como una sucesi�n de pixels formando una red de l�neas, algunas confluyentes y otras no, como en el caso de la red de drenaje de la misma figura. Un patr�n espacial se forma, cuando se tiene un conjunto de patrones espectrales con caracter�sticas semejantes a trav�s de una imagen digital multiespectral. Por tanto en una misma imagen pueden ocurrir varios patrones espaciales con semejanza; as�, por ejemplo, podr�a haber varios lagos o varias zonas boscosas de diferentes especies de �rboles, de tal forma que cada lago o cada zona boscosa formen de por s� un patr�n espacial o estructura quasielemental. Con esto que hemos discutido podemos introducir ahora un nuevo concepto: al conjunto de patrones espaciales o de estructuras quasielementales con patrones espectrales parecidos se le denomina clase de cobertura. Esta definici�n es adecuada para cuando el patr�n espacial presenta condiciones de homogoneidad, cuando los patrones espectrales que forman la clase de cobertura tiene caracter�sticas parecidas. Por ejemplo, si los lagos contienen todos ellos la misma calidad de agua o si los bosques tienen la misma especie de �rboles formar�n una clase de cobertura; si no fuera as�, habr�a tantas clases de cobertura como tipos de agua hubiera o especies de �rboles se presentar�n. Sin embargo, hay casos notables donde no se tienen condiciones de homogeneidad; este es el caso, de una radiograf�a en donde los huesos o alg�n otro tejido no presentan en general una clase de cobertura pareja, sino que m�s bien se muestran con variaciones de tono. �C�mo es entonces que un ser humano distingue a pesar de ello los diferentes huesos y los asocia con una misma clase de cobertura? Pues bien, esto se debe a que el cerebro humano no s�lo est� entrenado para distinguir variaciones de tono y de color, sino tambi�n otras cualidades con base en el contexto en el que se encuentra �l o los objetos que le interesan. Esto significa que los huesos pueden ser distinguidos por su tono, por su forma, por su textura, por el �rea que ocupan y por la frontera definida que presentan con respecto al resto de los tejidos. En otras palabras, los huesos son percibidos con base en las caracter�sticas espectrales del patr�n espacial que forman, por la textura que presentan y por su morfolog�a. En este ejemplo queda claro que las variaciones espectrales y las espaciales est�n interrelacionadas estrechamente y que es adecuado entender a una imagen como el conjunto de patrones espaciales y espectrales, aunado a la interrelaci�n que guardan entre ellos. Ahora ya puede ser ampliada nuestra definici�n de clase de cobertura para incluir casos generales como el de los huesos de una radiograf�a. Diremos entonces que una clase de cobertura es la manifestaci�n espacial de patrones espectrales con variaciones continuas de valor en un contexto de textura y de morfolog�a parecidas.

Figura 23. Regi�n del semi�rido mexicano, al norte de San Luis Potos�, captada por el sat�lite Landsat 2.

La figura 23 es una impresi�n fotogr�fica de un plano de color o banda de una imagen digital multiespectral registrada por el sensor satelitario Landsat, en donde, para esta representaci�n visual, se utilizan 128 niveles de gris, correspondiendo al negro el valor cero y al blanco el valor 127. Dicha imagen, tomada desde un altura de poco m�s de 900 km sobre la superficie terrestre, muestra una zona que se encuentra al norte de la ciudad de San Luis Potos� y cubre parte de una regi�n del semi�rido mexicano. La imagen se muestra como aparentemente continua, pero el tama�o f�sico asociado a cada pixel, en esta representaci�n visual, es tan peque�o que no puede distinguirse en esta impresi�n fotogr�fica. Esta figura es un buen ejemplo para poner en pr�ctica los conceptos desarrollados hasta ahora, adem�s de que nos permitir� aplicar claramente los elementos de an�lisis para entender la estructura de esta imagen de acuerdo a un fin espec�fico.

Aun en este ejemplo sencillo donde s�lo se considera un plano de una imagen multiespectral compuesto originalmente por cuatro bandas, podemos distinguir diversos patrones espectrales que se presentan bajo diferentes tonalidades de gris. En el cuadrante inferior derecho pueden observarse varias estructuras de aspecto circular que presentan un tono muy oscuro, casi negro; estas estructuras forman un �nico patr�n espectral y constituyen en conjunto una clase de cobertura. A partir de aproximadamente el centro de la imagen y yendo hacia el cuadrante superior izquierdo se puede apreciar otra clase de cobertura con un tono menos oscuro, el cual, a diferencia de la anterior, se encuentra m�s o menos conectada desde el punto de vista espacial. A su vez, esparcidos a trav�s de la imagen, en diversas tonalidades de gris, aparecen varios patrones espectrales que forman clases de cobertura no conectadas espacialmente; dichas tonalidades representan varias coberturas vegetales con diferentes densidades en cuanto al �rea proporcional de la escena que ocupan. En el otro extremo, en tonos de gris muy claros casi blancos, e encuentran un par de regiones de aspecto circular: una casi en el centro de la imagen y la otra en el cuadrante superior derecho; estas dos regiones, que representan lechos de lagos secos, adem�s de un conjunto de l�neas que indican caminos y cauces secos de r�os, forman otra clase de cobertura que tampoco est� conectada espacialmente. En este sencillo ejemplo de clasificaci�n espectral podemos observar varias cosas: en primer lugar es claro que en esta �ltima clase de cobertura est�n incluido tres tipos diferentes de objetos: los lechos, los cauces y los caminos, lo que nos ense�a que una clase espectral (clase de cobertura) no necesariamente est� relacionada un�vocamente con un solo objeto de la escena, sino que en general lo estar� con varios de ellos. Otro aspecto interesante es el de las clases que, teniendo diferentes tonalidades de gris, representan en forma aproximada varias densidades de vegetaci�n. En este caso, la clase espectral no est� constituida por objetos de diferente forma, como en el caso anterior, sino por la suma proporcional de dos clases de ellos: la de la vegetaci�n y la del suelo, y que diferentes densidades implican m�s bien una variaci�n en la proporci�n de estos objetos desde el punto de vista del �rea que ocupan en cada CIV de la escena. Al agregar m�s bandas, hasta considerar todas las que componen una imagen multiespectral satelitaria (cuatro en el ejemplo de la Figura 23), es posible que las clases de cobertura se separen o fraccionen; de esta manera es probable que los lechos de los lagos se diferencien de los cauces de los r�os, pero tambi�n que �stos se sigan confundiendo con los caminos. Esto se debe a que de banda a banda un mismo objeto presenta diferentes tonalidades de gris, y que si en una banda se confunde con otros objetos, en otra tal vez pueda diferenciarse, de tal manera que al considerar la imagen multiespectral en su conjunto se pueden distinguir una mayor variedad de objetos que si �nicamente se considera una banda por separado. Aun as�, casi nunca puede decirse que una clase de cobertura corresponde nada m�s a un solo objeto, puesto que recordemos (Figura 11) que el sensor remoto mide la energ�a luminosa que proviene de un CIV, el cual, para el caso de una imagen satelitaria moderna, puede tener 30 x 30 m², adem�s de que, como puede verse, lo m�s probable es que en �l haya varios objetos. As� pues, en un CIV puede haber algunos �rboles, suelo y rocas; todos estos objetos contribuyen, en forma proporcional, al �rea que ocupan dentro del CIV y a la energ�a luminosa que, finalmente, mide el sensor remoto. Nada m�s en ejemplos como el de los lechos o de los lagos o en el caso de cuerpos de agua donde el �rea que cubren es mucho mayor que el tama�o del CIV puede asegurarse que la clase de cobertura contiene un solo objeto de la escena, y esto, claro est�, en el supuesto de que un lecho o un cuerpo de agua no se confunde con alg�n otro objeto que tenga caracter�sticas espectrales similares. En este caso diremos entonces que una clase de cobertura se equipara con una clase espectral individual; en general consideraremos que una clase de cobertura est� compuesta por varios objetos de la escena o por varias clases espectrales. Algo m�s compleja es la situaci�n que se presenta en la formaci�n de una radiograf�a, ya que los rayos X pasan a trav�s del tejido �seo y del tejido blando; en este caso la energ�a que mide el sensor sobre el CIV correspondiente no es ya la superposici�n proporcional de las respuestas espectrales de los objetos que se encuentran en �l, puesto que aqu� ambos tejidos lo cubren enteramente; esto se debe a que los rayos X los atraviesan y no son reflejados como en �l caso de una escena terrestre iluminada por luz visible. Por tanto, en una radiograf�a la superposici�n de respuesta espectrales de los objetos contenidos en un CIV ya no es lineal, depende m�s bien de la manera como interaccionan los rayos X, primero con el tejido blando, despu�s con el �seo y al final nuevamente con el tejido blando. En otras palabras, estos rayos X al llegar al tejido �seo llevan ya informaci�n del tejido blando, puesto que ya interaccionaron con �sta, y posteriormente llevan informaci�n del tejido blando y del �seo; los rayos X interaccionan con el tejido blando que est� de un lado del tejido �seo, despu�s interaccionan con �ste y finalmente con el tejido blando que se encuentra del otro lado del tejido �seo. Sum�mosle a estos hechos el que ambos tejidos tienen espesores variables y que se encuentran a diferentes distancias de la fuente de rayos X y tendremos una situaci�n compleja, dif�cil de analizar, en forma automatizada. Todo esto hace que en ning�n caso de radiograf�a se plantee que una clase de cobertura corresponde �nicamente a un s�lo objeto o clase espectral.

Hemos estudiado hasta ahora los datos que est�n relacionados con los patrones espectrales de la figura. 23 y hemos dilucidado algunos aspectos interesantes de la escena, pues el an�lisis, clasificaci�n y segmentaci�n de dichos patrones nos han permitido entender varias caracter�sticas importantes de los objetos de la escena y de su comportamiento a partir de c�mo son vistos por un sensor remoto a trav�s de cada CIV. La naturaleza cuantitativa de la imagen digital correspondiente a la escena de inter�s es la que hace posible dicha clasificaci�n espectral, la que conduce, a su vez, a la separaci�n o segmentaci�n de varias clases de cobertura. Esta segmentaci�n es la que da lugar finalmente a que puedan ser extra�das varias propiedades de la clase de cobertura, tales como extensi�n o �rea cubierta, localizada en la escena y frontera con otras clases; estos datos, junto con medidas puntuales hechas directamente en la escena, son los que dan informaci�n sobre la situaci�n o aspecto que presentan los diferentes objetos del paisaje, como ya se discuti� en algunos ejemplos anteriores expuestos. La clasificaci�n espectral deja pendientes, sin embargo, algunas ambig�edades que s�lo pueden ser resueltas cuando se toman en cuenta las propiedades de los patrones espaciales, esto es cuando se integran al an�lisis espectral las consideraciones pertinentes en cuanto a textura y morfolog�a de tales patrones.

En cuanto a la morfolog�a existe una clara diferencia que presenta un camino con respecto a la forma de los cauces de los r�os y a la forma de los lechos de los lagos secos y que es lo que permite segmentar en tres clases diferentes lo que antes era una clase obtenida por consideraciones puramente espectrales. Al agregar consideraciones de forma lo que estamos haciendo es poner en m�s planos (Figura 22) estructuras cada vez m�s elementales, tan elementales como queramos o como nos lo permita nuestra capacidad de an�lisis automatizado, ya que en algunas ocasiones no se requiere de una s�ntesis de la imagen (Figura 22) con un detalle demasiado elevado, y en otras la dificultad de tipo computacional es tan grande que hace imposible la separaci�n de la imagen en una cantidad mayor de un n�mero dado de planos o estructuras quasielementales. Tal vez se podr�a decir que en el otro extremo de nuestro an�lisis sobre la morfolog�a se encuentra la consideraci�n de que la forma de los lechos de los lagos se confunde con la forma de los patrones oscuros que se encuentran en el cuadrante inferior derecho, y que con esto se produce, aparentemente, un retroceso en el proceso de segmentaci�n que deseamos realizar sobre la imagen digital original. En apariencia, la consideraci�n de la forma nos hace retroceder en la s�ntesis deseada, pero aqu� sucede algo similar a lo que pas� cuando consideramos los aspectos espectrales de la imagen: el considerar un solo tipo de clasificaci�n conduce necesariamente a ambig�edades. El uso combinado de la clasificaci�n espectral y de la clasificaci�n morfol�gica debe entenderse en el sentido de la utilizaci�n de ambas clasificaciones o de una de ellas; en todo caso la que proporcione la mejor segmentaci�n. La separaci�n de los lechos, cauces y caminos es un ejemplo de la aplicaci�n de la clasificaci�n espectral seguida de la clasificaci�n morfol�gica, pero, en el caso de los lechos y de los patrones oscuros mencionados, la decisi�n est� sobre una de las clasificaciones: la espectral. Cuando el uso combinado de estos criterios de clasificaci�n, en el sentido arriba expuesto, no permite segmentar m�s la imagen, es decir, no permite definir estructuras m�s elementales, decimos entonces que hemos agotado nuestra capacidad de an�lisis l�gico. Aqu� hay que hacer una distinci�n clara entre este tipo de capacidad y la capacidad de an�lisis computacional, puesto que puede suceder, y de hecho sucede en algunos casos, que la estructura de cierto patr�n espacial est� poco clara o poco definida, de tal manera que la clasificaci�n de su forma por medios automatizados arroje resultados ambiguos, aun cuando, tal vez, por medio de la interpretaci�n humana directa es posible la clasificaci�n correspondiente. En general, la limitante en la capacidad de an�lisis, pero no por ello en la rapidez, se encuentra, quiz�s dada por problemas en la implantaci�n computacional de los esquemas l�gicos de an�lisis, o quiz�s, en que no se ha logrado todav�a imitar con la adecuada eficiencia los criterios cerebrales de interpretaci�n humana.

La clasificaci�n con base en consideraciones de textura a�ade elementos interesantes al an�lisis de la imagen digital mostrada en la figura 23. De nueva cuenta, aquellas regiones oscuras se confunden con las que presentan el tono m�s claro, puesto que la textura para ambos extremos de tono se presenta en un aspecto similar, haciendo notar que aleda�as a las zonas m�s claras se encuentran manifestaciones texturales de aspecto muy peculiar que denotan un relieve del terreno diferente al de los lechos de los r�os en donde la superficie es bastante plana, y esta diferencia se presenta aun cuando el tipo de suelo sea aparentemente el mismo. Este hecho nos ense�a que en lo que a la superficie de la Tierra se refiere, la textura es un indicador de la topograf�a del terreno, y la topograf�a a su vez tiene que ver con propiedades geof�sicas de la misma superficie, propiedades que se refieren b�sicamente a la dureza del suelo y a las fuerzas que modelan el relieve de tal superficie. En el caso de una radiograf�a, la textura que presenta una determinada regi�n del sistema �seo puede dar informaci�n acerca del estado de desarrollo de los huesos, o del estado de salud en el que se encuentren. Tanto la superficie de la Tierra como un tejido humano determinado presentan una variedad de texturas relacionadas con propiedades geof�sicas y biom�dicas relativamente bien conocidas, de tal manera que la clasificaci�n textural es un elemento de informaci�n m�s en el estudio de un sistema f�sico por medio de percepci�n remota. Los cauces de los r�os y los caminos se ven como l�neas quebradas y rectas respectivamente y �stas son tan delgadas que cabe preguntarse si se puede asociar una textura a un patr�n espacial con estas caracter�sticas. Hab�amos dicho que la textura estaba determinada por tres aspectos en una imagen: la frecuencia de cambio de tono, la direcci�n del cambio y el contraste de un pixel con sus vecinos pr�ximos; de ah� que una l�nea, ya sea recta o quebrada, sea considerada como un caso particular y especial de un conjunto de texturas. Tal vez tengamos la tendencia a pensar que una clase de textura requiere, para ser considerada como tal, de un patr�n que presente un aspecto repetitivo de una u otra manera y, sin embargo, en el caso de una sola l�nea no se tiene tal repetici�n, aunque de todas maneras satisface los tres aspectos determinados para que exista una clase de textura; es debido a estas consideraciones que decimos que una l�nea es un caso particular y especial del concepto de textura. Con base en estos mismos criterios aplicados al caso de una l�nea, puede decirse que en el resto de la imagen (Figura 23) se tienen tres o cuatro texturas m�s relacionadas con la densidad de la vegetaci�n; pues aunque el aspecto "granuloso" es semejante para toda la cobertura vegetal, no as� el contraste que varía de una densidad a otra. Los criterios completamente diferentes para establecer una clasificaci�n espectral y una clasificaci�n textural hacen que al menos en el caso de la cobertura vegetal de la figura 23, la segmentaci�n que producen sea m�s bien complementaria y no excluyente.

�Qu� podr�amos decir ahora, en forma comparativa, de las tres clasificaciones posibles: espectral, textural y morfol�gica, que pueda ser aplicable en el proceso de an�lisis de una imagen digital multiespectral? Para responder a esto consideremos la Tabla 2 donde se muestran varios elementos de informaci�n f�sica acerca del terreno, y que aporta cada clasificaci�n para el caso de una imagen satelitaria de la superficie terrestre.

Tabla 2. Matriz comparativa del tipo de clasificaci�n en una imagen digital vs atributos del terreno.

Elemento de información
Clasificación	Topografía	Reflectancia	Actividades del hombre	Cobertura vegetal	Conjunción suelo/vegetal	Red de drenaje
Textural	X		X	X	X	X
Espectral		X	X	X	X	X
Morfológica			X			X

El atributo cobertura vegetal se considera aqu� para cuando se tienen densidades de vegetaci�n muy altas, lo suficiente para que cubra enteramente el suelo, y, por conjunci�n suelo/vegetaci�n se entiende el aspecto f�sico que presenta un cierto tipo de vegetaci�n desarrollada sobre un cierto tipo de suelo para una variedad amplia de densidades de vegetaci�n, pero sin que �sta cubra totalmente al suelo. Las condiciones topogr�ficas y del tipo del suelo determinan no nada m�s la especie o especies vegetales presentes, sino tambi�n el aspecto que presentan en cuanto a la textura, adem�s de que la respuesta espectral ser� la combinaci�n ponderada de las respuestas individuales de la vegetaci�n y del suelo, como ya se hab�a mencionado. En el caso de que un atributo sea cubierto por m�s de una clasificaci�n, debe entenderse que es en el sentido complementario a como se discuti� m�s arriba. Debe quedar claro que cada clase de imagen tiene un conjunto de atributos predeterminados por el contexto bajo el cual se adquiri� la informaci�n de la escena correspondiente y que, una vez definido dicho conjunto, la matriz comparativa, an�logamente a la de la Tabla 2, se construye con base en las caracter�sticas particulares del problema que se desea analizar a trav�s de la imagen digital respectiva. El manejo de una tabla de clasificaci�n como la Tabla 2 constituye un recurso general y amplio de una metodolog�a adecuada para el an�lisis de una escena dada, ya que es a trav�s de estas tres posibles clasificaciones que se realiza la segmentaci�n de la imagen digital correspondiente a la escena y son las estructuras quasielementales las que dan informaci�n cuantitativa de cada clase de objetos en la escena. Si una o varias estructuras de este tipo cambian en la imagen digital, tambi�n lo hace la clase o las clases de objetos correspondientes en la escena. La manera particular como se presentan las estructuras quasielementales de una imagen define claramente la situaci�n en la que se encuentran los objetos de la escena en el contexto de un problema dado, es decir que las estructuras correspondientes, digamos al sistema �seo, se presentan de una manera caracter�stica y �nica dependiendo de la situaci�n general de salud en la que se encuentre dicho sistema. En este contexto podemos decir que la manera particular en la que se presentan las estructuras quasielementales de una imagen digital multiespectral definen lo que llamaremos estado espacial de la imagen, y que el camino de cualquiera de dichas estructuras da como resultado un cambio en el estado espacial de la imagen, lo que se traduce en que un cambio en el estado espacial implica que en la escena ha ocurrido una modificaci�n y que por tanto el an�lisis correspondiente arrojar� resultados diferentes. Todo esto dejando claro que, como la imagen ha sido sintetizada en estructuras quasielementales, se puede definir y cuantificar exactamente de qué tipo y de qué extensi�n ha sido la modificaci�n que ha experimentado la escena.

Veamos ahora c�mo se pueden resumir esquem�ticamente los conceptos desarrollados aqu� para el an�lisis de una escena; para ello consideremos la Tabla 3.

Tabla 3. Orden l�gico para el an�lisis de una imagen digital y para la evaluaci�n integral de la escena correspondiente.

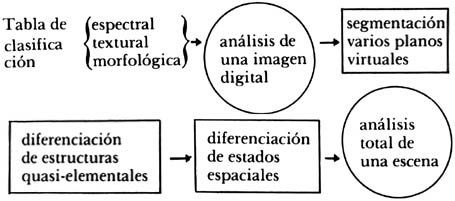
En la Tabla 3 se han marcado con sendos �valos el an�lisis de una imagen digital y, por tanto, el de la escena correspondiente, puesto que el an�lisis de la primera implica el de la segunda. La clasificaci�n en tres posibles contextos: espectral, textural y morfol�gica es el comienzo del proceso, pues la tabla de clasificaci�n correspondiente se construye a partir de la imagen dada y de los atributos del problema; la soluci�n correspondiente se encuentra por medio de la segmentaci�n de la imagen digital en estructuras quasielementales hasta llegar a la evaluaci�n de la situaci�n de la escena a trav�s de la diferenciaci�n del estado espacial correspondiente a dicha situaci�n. No debemos olvidar, desde luego, que el an�lisis de la escena requiere de la observaci�n directa de un n�mero selecto de objetos que se encuentren en la misma.

Se han vertido hasta aqu� una serie de conceptos muy importantes para comprender lo que es la percepci�n remota, la cual involucra en forma integral la captura de la imagen de una escena que se encuentre bajo condiciones relativamente bien conocidas, el manejo de la m�s moderna tecnolog�a para el dise�o y construcci�n de los sensores remotos adecuados a cada problema y, desde luego, el an�lisis de las im�genes digitales por medios automatizados utilizando una computadora digital. Dichos conceptos nos permiten retomar la definici�n de la percepci�n remota y replantearla en t�rminos m�s amplios y generales; para esto diremos que la percepci�n remota espacial y aerotransportada est� dise�ada para obtener datos, en un experimento controlado, acerca de una escena, la que puede estar constituida por una superficie f�sica o virtual. Las medidas involucradas a distancia no son encontradas para establecer nuevas leyes f�sicas, sino m�s bien para identificar, discriminar y caracterizar (matem�tica y f�sicamente) las clases de objetos que yacen sobre dicha superficie. Las observaciones hechas de esta manera se refieren b�sicamente a las propiedades espectrales y espaciales (texturales y morfol�gicas) de los mencionados objetos. Es posible que varias de las observaciones sean repetitivas, con lo que se pueden considerar tambi�n las propiedades temporales de la escena en el conjunto de medidas. La interacci�n de la superficie sensada con los mecanismos de "iluminaci�n" est� en buenos t�rminos bien entendida. La interacci�n puede ser complicada para sistemas activos, como el radar, las se�ales ac�sticas, los rayos X o los haces corpusculares, o simples para sistemas pasivos, como es el caso de la teleobservaci�n de la escena terrestre cuando se encuentra iluminada por la radiaci�n solar. En cualquier caso, el mecanismo de generaci�n de im�genes depende, primeramente, de la interacci�n arriba mencionada, segundo, de la geometr�a particular (Figuras 1 y 2) de iluminaci�n; fuente-objeto de la escena/sensor remoto, y tercero, del m�todo de observaci�n y del dispositivo sensor. Las propiedades espaciales y espectrales de la escena est�n quasipermanentemente registradas en forma digital o anal�gica y la imagen resultante contiene mucha informaci�n relacionada con los tres factores mencionados. El proceso de formaci�n de im�genes arriba descrito es aplicable tanto en percepci�n remota, como en la f�sica nuclear, las ciencias biom�dicas y en la industria, pues, como se ha visto a lo largo de este trabajo, todas estas ramas de la ciencia y la tecnolog�a utilizan las t�cnicas y la metodolog�a de la percepci�n remota en el desarrollo experimental de la investigaci�n b�sica y aplicada. Por razones hist�ricas, la percepci�n remota es actualmente un t�rmino reservado para cuando se estudia el medio ambiente geof�sico y para cuando las observaciones mencionadas se hacen desde el espacio y desde el aire.

Figura 24. La porci�n inferior de esta figura muestra la banda 5 (rojo) de una imagen satelitaria que ha sido degradada por la interferencia de la luz solar por la atmósfera. En la parte superior se muestra la misma pero restaurada despu�s de haber modelado f�sicamente dicha interacci�n.

Es necesario insistir que la percepci�n remota es una ciencia aparte con m�todos y elementos propios que han sido aplicados exitosamente en otras ramas de la investigaci�n experimental. Cabe a�adir tambi�n que cuando esto se ha hecho as� se habla en t�rminos generales de teleobservaci�n: de la generaci�n de im�genes digitales multiespectrales acerca de una escena cualquiera. El proceso de extracci�n de informaci�n (an�lisis de im�genes) est� conectado a los tres factores mencionados con anterioridad y a los mecanismos de degradaci�n (Figura 24) involucrados en la formaci�n de la imagen. El estudio y comprensi�n de esto facilita el camino hacia la evaluaci�n de las clases de objetos de la escena, de acuerdo a la representaci�n esquem�tica de la figura 25:

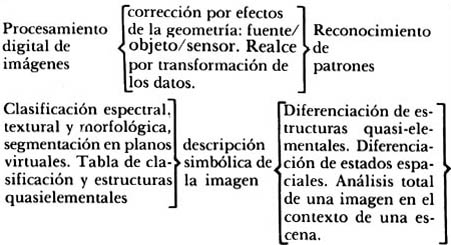
Figura 25. Etapas en el an�lisis de una imagen digital para la evaluaci�n y modelado de las clases de objetos de la escena.

Una vez que se obtiene la descripci�n simb�lica de una imagen o de su estado espacial, la relaci�n de una cierta cobertura de clase de objetos con un recurso particular puede no ser directa ni f�cil de encontrar en la mayor�a de los casos. Esto implica el modelaje del medio ambiente geof�sico relacionado a tal recurso natural. Cuando este modelaje se complementa adecuadamente con observaciones directas (apoyo de campo) acerca de las clases de objetos, entonces se puede obtener informaci�n valiosa acerca de la superficie sensada. Es en esta etapa en donde se puede realizar una planeaci�n adecuada de los recursos naturales por medio de un Sistema Geogr�fico de Informaci�n, con consecuencias muy importantes en el desarrollo socioecon�mico de un pa�s.

En forma global podemos decir tambi�n que la percepci�n remota se compone de cinco elementos b�sicos: el paisaje, la escena, el sensor remoto, el tratamiento de la informaci�n relativa a la escena y la modelaci�n (cuantificaci�n f�sica y matem�tica) de las clases de objetos relativos a aqu�lla con fines de conocimiento del paisaje. Todos estos elementos han sido ya discutidos, sin embargo es conveniente retomar algunos y considerarlos en otro contexto con el objeto de complementar y ahondar lo dicho hasta ahora. En lo que se refiere al sensor remoto podemos considerarlo como un dispositivo capaz de caracterizar adecuadamente la escena, y la lista de instrumentos (Tabla 1) que pueden clasificarse como tales es muy grande y variada: cubre desde la c�mara fotogr�fica hasta el explorador espacial m�s refinado. Pero lo m�s importante es que para caracterizar adecuadamente una escena es necesario que el sensor pueda medir un conjunto de variables f�sicas que aqu�lla contiene. Por supuesto no es indispensable ni pr�ctico que �ste mida todas las variables, pues una escena es com�nmente muy compleja y contiene una gran cantidad de ellas. Una caracterizaci�n adecuada ser� entonces aqu�lla que sea capaz de medir un n�mero selecto de variables que son de inter�s para el investigador, y cuyo papel es seleccionar y aislar la informaci�n necesaria y suficiente para entender el fen�meno que le interesa, a fin de comprender el comportamiento del paisaje en un problema espec�fico. Pero como un sensor remoto guarda su distancia respecto a la escena, las variables medibles por �l se reducen a dos: la intensidad y la energ�a de luz o radiaci�n emitida o reflejada por los objetos que se hallan en ella; la intensidad corresponder� a la brillantez y la energ�a al color (esto para el caso de la luz visible). As�, la percepci�n remota se reduce a medir la variaci�n espectral, espacial y temporal de la radiaci�n que proviene de la escena. La intensidad de esta radiaci�n, para cada energ�a, depende, en forma compleja, de los componentes de aqu�lla y de la intensidad de la radiaci�n que emite la fuente de iluminaci�n. En algunos casos es posible que la escena absorba parte de la radiaci�n incidente y despu�s de un cierto tiempo la reemita en una forma de energ�a diferente. Los sensores m�s sensibles (espectroradi�metros) permiten estudiar este fen�meno de absorci�n y reemisi�n. En general, para un CIV determinado de la escena y en un instante dado, se puede medir la intensidad de la radiaci�n que corresponde a cada valor de la energ�a, es decir a cada color de la luz incidente, obteniendo as� lo que se conoce como respuesta espectral de ese CIV.La finalidad del uso del sensor remoto consiste en medir esta respuesta para cada punto de la escena. A este conjunto de medidas se le llama imagen multiespectral digital de la escena. Dicho en otras palabras, el sensor, mediante un sistema optoelectr�nico, divide la regi�n del espectro de colores de la luz que proviene de ellas en varios intervalos llamados bandas y a cada uno le asigna un valor proporcional a la intensidad de la radiaci�n que proviene de cada CIV de la escena. Este valor de intensidad se aproxima, a su vez, mediante un convertidor que traduce la se�al anal�gica (continua) a un valor num�rico digital. Estos valores pueden ser por su parte almacenados en alg�n dispositivo conveniente, como una cinta magn�tica, o en el caso de un sensor satelitario, ser transmitidos a la estaci�n de rastreo del sat�lite m�s pr�ximo. El desglosar el espectro de luz en varias bandas o planos de color facilita la obtenci�n de informaci�n a partir de los datos de la escena, ya que el grado de luminosidad de cada uno de los elementos que la componen var�a de banda a banda, como ya se hab�a explicado. Este m�todo forma en un proceso en paralelo, varias im�genes de la misma escena, produciendo lo que se conoce como imagen multiespectral de la misma.

Para fines de representaci�n visual (despliegue) de la imagen digital multiespectral, en cada una de las bandas, puede asignarse a sus elementos o pixels un color arbitrario, lo que ayuda, entre otras cosas, a la clasificaci�n y realce de dichos elementos. La superposici�n de estas im�genes en un sistema de despliegue (Figuras 6, 18, 19, 20, 23 y 24) constituye una reconstrucci�n de la escena y la informaci�n contenida en tales bandas, separable o interrelacionada, permite el an�lisis (visual) y modelado (f�sico y matem�tico) de los objetos que la componen. Los datos de cada banda de la imagen multiespectral, con sus respectivas correlaciones acerca de todos los elementos de una escena, son numeros�simos, por lo que es necesario utilizar una computadora digital para que los procese. Un sistema de computaci�n con una programaci�n adecuada puede examinar y clasificar r�pida y sistem�ticamente los datos obtenidos por el sensor remoto. La potencialidad de un sistema de este tipo estriba en su capacidad para manejar la informaci�n cuantitativa relativa a la escena. Antes de evaluar las im�genes de �sta es necesario procesar los datos obtenidos por el sensor y prepararlos a fin de que puedan ser analizados. Esto se realiza en tres etapas: primera, la correcci�n de defectos debido a la distorsi�n de la geometr�a particular que guarda la plataforma y el sensor con la escena y la fuente de iluminaci�n; segunda, el realce por transformaci�n de los datos de la imagen con el objeto de poner en evidencia ciertos patrones en la imagen, y tercera la agregaci�n o clasificaci�n de los datos relativos a la escena. Una vez as� procesadas, las im�genes se encuentran listas para el trabajo de evaluaci�n y modelado, el que se realiza precisamente en la parte que se ha denominado descripci�n simb�lica de la imagen digital (Figura 25) y que culmina con la construcci�n de una tabla similar a la 2. El tratamiento de los datos relativos a la escena en el contexto de lo que se esquematiza en la figura 25 se realiza por medio de un paquete de programas formado por una variedad de algoritmos computacionales instalados en una computadora digital. Dicho paquete puede operar con los valores provenientes de cada banda que hayan sido adscritos a las repuestas espectrales de cada CIV de la escena. Mediante el examen autom�tico de estos valores, las �reas sobre ella que muestren respuestas similares pueden ser relacionadas, clasificadas y modeladas en el contexto del medio ambiente geof�sico, f�sico, biom�dico e industrial.

En principio, el comportamiento temporal de la respuesta espectral de los puntos de la escena, permitir�an identificar los elementos que la componen, con la sola limitaci�n de la resoluci�n espectral y espacial del sensor remoto. Ser�a una tarea formidable medir directamente la gran variedad de objetos, con sus respectivas variaciones estad�sticas, que forman los diferentes sistemas f�sicos susceptibles de estudio por medio de la percepci�n remota y posteriormente almacenar en un banco de datos el resultado de estas medidas con el objeto de utilizarlos en el an�lisis de los sistemas f�sicos mencionados. As�, es necesario establecer un compromiso entre la teleobservaci�n de la escena y las medidas directas efectuadas sobre ella misma. Las medidas directas son indispensables en la correcta identificaci�n de los objetos teleobservados. Las medidas directas o medidas puntuales son un conjunto de datos, tomados directamente sobre la superficie que forma la escena y que permiten establecer una correlaci�n un�voca entre los datos que produce el sensor y la realidad f�sica de la misma. Es claro que si se contara con "toda" la informaci�n directa de la escena, la percepci�n remota ser�a in�til por redundante, y que si las medidas puntuales fuesen desconocidas, los datos obtenidos por el sensor remoto no tendr�an todo el potencial y la utilidad que tienen cuando se combinan con dichas medidas puntuales. M�s a�n, con la carencia de este tipo de medidas, algunos datos del sensor remoto faltar�an de sentido por no saber exactamente a qu� corresponden. Las medidas puntuales sirven de calibraci�n al experimento realizado por medio de la percepci�n remota. Un factor muy importante en la percepci�n remota en geof�sica es la atenuaci�n de la luz proveniente de la Tierra debido a la atm�sfera y a las nubes. Aunque esta atenuaci�n se debe principalmente a la dispersi�n de la luz por las mol�culas que forman el aire, hay algunas regiones del espectro de luz donde se produce por absorci�n, fundamentalmente debida a mol�culas de agua, ozono, ox�geno y bi�xido de carbono. A esto hay que agregar que en el caso de las nubes la luz que proviene del Sol es reflejada hacia el espacio y no alcanza por tanto a iluminar la superficie terrestre. Estos problemas implican que las regiones del espectro de luz donde no hay absorci�n forman varias "ventanas" que se aprovechan para denominar las bandas m�s convenientes en operaci�n del sensor remoto (Tabla 4). As�, por ejemplo, en los Landsat 4 y 5 la banda n�mero 4 se ha reducido con respecto a la que utilizaban los Landsat 1 y 2 para evitar la absorci�n debida a las mol�culas del agua en semisuspensi�n en la atm�sfera terrestre. El problema que presentan las nubes es m�s complicado, ya que adem�s de la atenuaci�n por dispersi�n y absorci�n, la luz reflejada por ellas se superpone a la que proviene directamente de la tierra y que incide en el sensor remoto. Este efecto es muy importante, ya que en cualquier momento la Tierra se encuentra cubierta por nubes en un 50% de su superficie. Cuando la nube es delgada, y permite al menos un 50% de transmisi�n de la luz, es posible recobrar (Figuras 26(a) y 26(b), v�ase pliego a color) parte de la informaci�n que se encuentra debajo de ella. En los Landsat 3, 4 y 5, una banda en el infrarrojo t�rmico ayudar�, en parte, a resolver esta dificultad puesto que las nubes y la atm�sfera son m�s transparentes en esta regi�n del espectro de luz invisible al ojo humano, que en aquella regi�n de la luz visible.

Tabla 4. Comparaci�n de algunos datos de plataformas espaciales y sus respectivos sensores.

Plataforma Dato	Skylab	Landsat 1 y 2	Landsat 3	Landsat 4 y 5	SPOT	Nimbus 7	GOES 6
Fecha de lanzamiento	Febrero, 1973	Julio,1972 y Enero 1975	Marzo, 1975	Julio, 1982 y Marzo, 1984	Noviembre 1985	Octubre, 1978	Abril, 1983
Altura sobre la tierra	435 km	920 km ambos	912 km	700 km ambos	822 km	955 km	36000 km
Periódo de la órbita	93 minutos	103 minutos ambos	103 minutos	99 minutos ambos	101 minutos	107 minutos	24 horas
Tamaño del elemento de resolución	variable y comparable a los Landsat 1 y 2	57x79 m²	57x79 m² 238x238 m² para la 5a. banda.	30x30 m² 120x120 m² para la 6a. banda	20x20 m² 10x10 m² para la 4a. banda.	800x800 m²	14x14 km² para la 1a. banda,8x8 km² para la 2a. banda
Tamaño de la imagen	variable	185x185 km²	185x185 km²	185x185 km²	60x60 km²	16000 x 16000 km²	18000 x 20000 km²
Bandas espectrales	13 bandas espectrales entre 0.4 y 12.5 mm	1)0.5-0.6mm 2)0.6-0.7 3)0.7-0.8 4)0.8-1.1	1)0.5-0.6mm 2)0.6-0.7 3)0.7-0.8 4)0.8-1.1 5)10.4-12.6	1)0.45-0.52mm 2)0.52-0.60 3)0.63-0.69 4)0.76-0.90 5)1.55-1.75 6)10.4-12.5 7) 2.08-2.35	1)0.50-0.59mm 2)0.61-0.69 3)0.79-0.90 4)0.51-0.73	1)0.43-0.45mm 2)0.48-0.50 3)0.51-0.53 4)0.55-0.57 5)0.58-0.60 6)0.66-0.68 7)0.75-0.79 8)0.84-0.89	1)0.55-0.75mm 2)10.5-12.5

Nota: la correspondencia aproximada "colores" y longitudes de onda es la siguiente:

Violeta	0.40-0.45 mm	Amarillo	0.56-0.59 mm	Infrarrojo cercano	0.70-3.0
Azul	0.45-0.51	Anaranjado	0.59-0.63	Infrarrojo t�rmico	3.0-14.0
Verde	0.51-0.56	Rojo	0.63-0.70

Hemos desarrollado y estudiado hasta ahora los elementos m�s importantes para el an�lisis de una imagen multiespectral con el objeto de entender los mecanismos del funcionamiento de la escena y del paisaje. Cabe aclarar que las dificultades matem�ticas y computacionales para el an�lisis digital de una imagen multiespectral pueden ser enormes. De hecho en algunos casos los requerimientos en computaci�n y matem�ticas son de una importancia tal que implican que un laboratorio de percepci�n remota necesite de personal altamente calificado y requiera de los m�s avanzados sistemas computacionales. Por otro lado diremos tambi�n que de las clasificaciones mostradas en la Tabla 2, la que es relativamente m�s f�cil de llevar a cabo es la espectral, ya que la definici�n de respuesta espectral es de una naturaleza que no permite ambig�edades. La definici�n que se dio aqu� es claramente cuantitativa y conduce a establecer reglas precisas para la separaci�n de clases espectrales que finalmente pueden ser asociadas con las de cobertura de la escena, de acuerdo a la serie de ejemplos dados con anterioridad. Las dificultades matem�ticas y computacionales se incrementan a medida que se enfrentan problemas de clasificaci�n textural o morfol�gica y esto se debe b�sicamente a que a�n no se comprenden cabalmente los mecanismos que utiliza un ser humano para analizar en general una imagen. A medida que se vayan entendiendo dichos mecanismos, se ir�n eliminando elementos de subjetividad y se obtendr�n criterios claros y cuantitativos para las clasificaciones textural y morfol�gica; esto traer� como consecuencia un incremento notable en la velocidad de an�lisis, sin dejar de lado que, en una simbiosis estrecha, entender los mecanismos cerebrales de reconocimiento de patrones tambi�n traer� un mejoramiento en el dise�o de los sistemas computacionales, tanto en su arquitectura como en los lenguajes de operaci�n de la computadora respectiva.

En la captura y registro de una imagen multiespectral de una escena dada existen siempre fen�menos o medios de interferencia (Figuras 24 y 26) que degradan de cierta manera la informaci�n contenida en la imagen digital. �ste es el caso mostrado en la figura 24, en donde se presenta una impresi�n fotogr�fica del plano de color o banda que corresponde al rojo de una imagen multiespectral satelitaria de cuatro bandas. De hecho, todas las im�genes satelitarias son degradadas por la interacci�n de la luz con la atm�sfera, lo que consiste en que la luz se dispersa al interaccionar con las mol�culas que componen el aire de aqu�lla, siendo mayor el grado de dispersi�n para el azul y disminuyendo gradualmente hacia el rojo, lo que significa que los planos de una imagen multiespectral estar�n degradados de manera diferente de acuerdo al filtro de color con que fueron tomadas. Al modelar f�sicamente dicha interacci�n se logra entender y cuantificar la dispersi�n de la luz solar en funci�n del color y de las componentes atmosf�ricas, lo que permite entonces restaurar la imagen al estado que tendr�a si no hubiera ocurrido dicha dispersi�n. La restauraci�n consiste en construir una imagen que llamamos restaurada a partir de la imagen degradada y de la comprensi�n del fen�meno de degradaci�n, de tal forma que el producto resultante sea como si el fen�meno de degradaci�n hubiese estado ausente al momento de la captura de la escena correspondiente. En la mayor�a de los casos de degradaci�n los efectos se manifiestan como si la imagen resultante estuviese borrosa, fuera de foco o carente de contraste. Al observar la parte superior de la figura 24 vemos que estos efectos han sido minimizados. En otros casos de degradaci�n la imagen resultante puede aparecer como "embarrada" por el movimiento relativo entre el sensor y la escena, como es el caso de un sensor orbital donde la captura de �sta debe hacerse en forma extremadamente eficiente para minimizar este efecto de "embarramiento". La figura 26 nos ense�a un caso interesante de degradaci�n, puesto que en la parte (a) se puede apreciar una imagen similar a la mostrada en la figura 24, pero con una nube cubriendo la parte inferior. Esta nube es bastante delgada, es decir deja pasar m�s del 50% de la luz que proviene del sol. Aun as� constituye un verdadero obst�culo; el resultado es que dif�cilmente se aprecia lo que se encuentra debajo de dicha nube. Con un modelo matem�tico y f�sico, una buena parte de la nube ha sido "removida" (Figura 26(b)), logrando con esto una imagen restaurada. Tal restauraci�n es s�lo para casos relativamente simples, puesto que para nubes gruesas o con espesor altamente variable es pr�cticamente imposible recobrar la informaci�n pertinente a la imagen digital. En el caso de la radiograf�a de un ser humano o de un motor en donde se pretenden observar patrones internos como huesos o defectos, los mecanismos de degradaci�n son m�s complejos, ya que el medio o los medios de interferencia est�n estrechamente ligados con los patrones que se desean estudiar. Aun en este caso la restauraci�n es posible cuando son bien conocidas las circunstancias bajo las cuales fueron tomadas las radiograf�as.