II. LAS COSTUMBRES DE LAS CARGAS

II. LAS COSTUMBRES DE LAS CARGAS

EN ESTE cap�tulo examinaremos los movimientos que siguen las cargas en presencia de campos magn�ticos.
Las cargas el�ctricas se mueven en un campo magn�tico girando alrededor de l�neas imaginarias, llamadas l�neas del campo magn�tico. Una carga conserva su velocidad en la direcci�n de estas l�neas del campo. Al mismo tiempo, es obligada a girar alrededor de las l�neas en forma de un movimiento de tirabuz�n. La fuerza magn�tica obliga a las cargas a girar en direcci�n perpendicular a las l�neas del campo, lo cual provoca ese movimiento curvil�neo.
Una fuerza perpendicular a la direcci�n de movimiento produce un movimiento curvil�neo. Pensemos en una piedra que se ata del extremo de una cuerda y se hace girar jalando la cuerda del otro extremo. En este ejemplo se verifica que, para mantener el movimiento circular, es necesario que la fuerza de tensi�n de la cuerda vaya dirigida en una l�nea perpendicular a la circunferencia que recorre la piedra.
Por ser perpendicular a la direcci�n de movimiento, la fuerza magn�tica no cambia el tama�o de la velocidad, �nicamente modifica la direcci�n del movimiento. La fuerza magn�tica es asimismo perpendicular a la direcci�n de las l�neas del campo magn�tico. La fuerza magn�tica sobre una carga formar�a un �ngulo recto con la direcci�n de la br�jula en el mismo sitio.
Las cargas de distinto signo giran en direcciones opuestas en presencia de un campo magn�tico, y las part�culas neutras no se ven afectadas por el campo magn�tico. Una forma frecuente de distinguir a las part�culas es seguir sus huellas en presencia de un campo magn�tico: las part�culas neutras siguen una l�nea recta y las part�culas cargadas se mueven en c�rculos con ejes perpendiculares al campo y con curvaturas diferentes, seg�n el signo de la carga. En el cap�tulo precedente se vio c�mo Thomson usa esta idea para descubrir la relaci�n entre las masas del prot�n y del electr�n y c�mo Aston encuentra dos tipos diferentes de is�topos del gas ne�n.
Para poder ver la trayectoria que sigue la carga, se hace pasar �sta por una c�mara de burbujas, una emulsi�n fotogr�fica, una c�mara de niebla, etc. La part�cula deja una huella al provocar cambios qu�micos o f�sicos a lo largo de su camino, como la condensaci�n de peque�as gotas en la c�mara de niebla.
Cuando se tiene una carga en movimiento en un campo magn�tico constante de tama�o B, este campo llena su espacio con l�neas paralelas. La carga se mueve en la direcci�n del campo con una velocidad constante —que incluso puede ser cero—, la misma mientras siga en ese campo constante. Pero s�lo en la direcci�n de la br�jula la velocidad es constante, otra cosa sucede en la direcci�n perpendicular. Al mismo tiempo que avanza con velocidad constante en la direcci�n del campo, la carga gira en un c�rculo con una velocidad perpendicular de magnitud fija pero de direcci�n rotante.

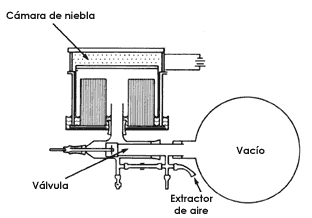
Figura 6. C�mara de niebla para observar la trayectoria de una carga.

Dicho c�rculo tiene un radio igual al producto de la masa por su velocidad perpendicular, divididos ambos por el producto del tama�o de la carga y el tama�o del campo. Esta propiedad puede verificarse por experimento y se escribe en forma simb�lica como

donde R, m, w, q, B, representan respectivamente los tama�os de radio, masa, velocidad perpendicular, carga y campo. El per�metro del c�rculo es igual a 2 por pi por el radio R, con pi igual aproximadamente a 3.1416. Este per�metro es recorrido con la velocidad w. Podemos entonces calcular el tiempo T que tarda en dar una vuelta debido a que el cociente del per�metro entre el tiempo T es la velocidad w. Se encuentra as�

f�rmula que nos dice simb�licamente la forma que se ha de calcular el tiempo que tardar� en dar cada vuelta: tomar el producto de 2 por 3.1416 por la masa dividido por el producto de la carga y el campo. Aqu� no pretendo recomendar al lector la pr�ctica de las tablas pitag�ricas de multiplicar. Quiero tan s�lo hacerle notar la relaci�n entre cantidades que se miden o conocen independientemente (pi). Estas relaciones u otras similares permiten predecir y al mismo tiempo controlar el movimiento, una vez que dichas relaciones se conocen y se han medido o deducido la mayor parte de las cantidades.
En este libro recordaremos frecuentemente que una carga se mueve sin fuerza magn�tica en la direcci�n del campo magn�tico y describiendo vueltas alrededor de las l�neas del campo.
Cuando el campo magn�tico no es constante, la carga sigue dando vueltas alrededor de las l�neas del campo con un radio variable, y en un tiempo tambi�n variable, debido a que ahora dejaron de ser constantes el campo B y la velocidad w. Las relaciones entre las cantidades R, m, w, q, B, T, etc., se siguen cumpliendo en forma aproximada.
Esta predilecci�n de las cargas por revolotear en tirabuz�n en torno de las l�neas del campo hace que en muchas ocasiones encontremos reunidas a cargas y l�neas del campo. A fin de estudiar en detalle el movimiento de cargas en campos magn�ticos se descompone el movimiento en un movimiento de rotaci�n alrededor de la l�nea del campo, en un movimiento de traslaci�n a lo largo de la l�nea del campo, y un movimiento de deriva que mueve la carga de una l�nea a otra. Como el movimiento de rotaci�n es generalmente mucho m�s r�pido que los otros movimientos, se acostumbra promediar el movimiento de giro como si la carga, en lugar de girar alrededor de la l�nea del campo, estuviera en su centro, movi�ndose solamente a lo largo de dicha l�nea o en un movimiento de deriva.
Esta idea viene a representar una simplificaci�n muy grande en el modelo descriptivo de dicho movimiento, ahorr�ndose el revoloteo, que complica bastante el control y la comprensi�n del camino seguido por el movimiento en s�. Se determina primero cu�l es el movimiento del centro de giro, y a este movimiento se le llama del centro gu�a. Su estudio se conoce como teor�a de la deriva.
Cuando las l�neas del campo magn�tico concurren en un punto o se aprietan como si fueran a concentrarse acontece un fen�meno especial. Las cargas que dan vueltas alrededor de las l�neas del campo, al irse acercando a la regi�n de convergencia, su radio de giro disminuye de tama�o y en un momento dado se ven obligadas por la fuerza magn�tica a alejarse de la concentraci�n de l�neas, aumentando ahora el radio de giro, conforme se alejan de la concentraci�n de l�neas. El centro gu�a rebota en la concentraci�n de las l�neas magn�ticas.
Este fen�meno se conoce como espejo magn�tico porque las cargas se reflejan al encontrarse con una concentraci�n de campo. Se ha sugerido construir botellas magn�ticas capaces de retener a las cargas por medio de reflexiones. Se construye un campo en forma de un huso y las cargas van y vienen reflej�ndose en los extremos del huso, donde se concentran las l�neas del campo. En el cap�tulo siguiente veremos c�mo el campo dipolar de la Tierra sirve como botella magn�tica que atrapa electrones y protones y forma con ellos dos cinturones de carga de signo diferente a su alrededor.
El ejemplo m�s sencillo de un espejo magn�tico es el campo llamado de monopolo. El campo magn�tico de monopolo es muy parecido en forma a la fuerza el�ctrica de Coulomb, pero mientras que la fuerza de Coulomb tiene la direcci�n del campo el�ctrico, la fuerza producida por un monopolo es perpendicular al campo magn�tico y a la velocidad, seg�n vimos previamente.
El movimiento de una carga en presencia de un monopolo se lleva a cabo como si la carga tuviera que moverse sobre un cono circular cuyo v�rtice coincide con la posici�n del monopolo. Las l�neas del campo magn�tico son rectas que concurren en el v�rtice del cono.

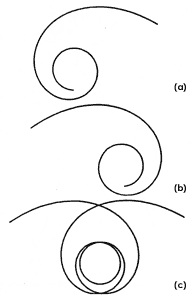
Figura 7. Vista de la carga desde el eje de simetr�a del cono (a) arribo (b) salida (c) superposici�n.

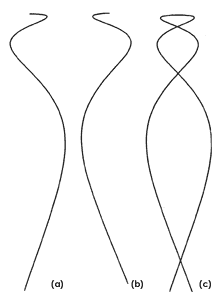
Figura 8. Vista lateral de la trayectoria sobre el cono (a) arribo (b) salida (c) superposici�n.

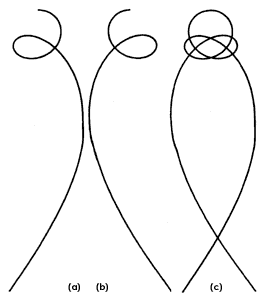
Figura 9. Vista de perspectiva de las figuras 7 y 8.

La fuerza magn�tica del monopolo obliga a la carga a seguir el camino m�s corto posible sobre la superficie del cono. Pero el cono es una superficie desarrollable —o desenrrollable—que se puede aplanar sin necesidad de estirar. Los caminos de las cargas, cuando se desenvuelve y aplana el cono, se ven como l�neas rectas sobre el plano. Vistas en el cono, esas l�neas de longitud m�nima se llaman geod�sicas. En las figuras 7, 8, 9 se observan diversas vistas del movimiento de una carga en un cono, la figura 7 es una vista desde el eje de simetr�a del cono.
La figura 10 muestra a la geod�sica del cono cuando �ste se ha aplanado. El lector puede usar esta figura como patr�n para construir un cono y visualizar las geod�sicas sobre �l.
El patr�n del cono es un �ngulo cuyas dos rectas van a hacerse coincidir en una generatriz del cono. Conviene dejar una ceja (sin doblar) en una de estas dos rectas para superponer sobre el otro lado del �ngulo y pegarla para formar el cono.
La geod�sica sobre el cono se dibuja en el plano como un segmento de l�nea recta que forma un tri�ngulo is�sceles con los dos lados del �ngulo. En la figura, es el segmento m�s cercano al v�rtice. Las restantes l�neas de la geod�sica se obtienen reflejando la l�nea anterior en los dos lados del �ngulo, de modo que las l�neas reflejadas formen el mismo �ngulo con la generatriz del cono que hace el lado del �ngulo.

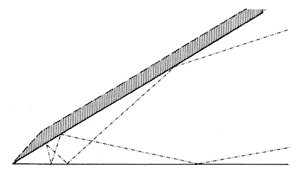
Figura 10. Geod�sica del cono cuando �ste se ha aplastado.

Se observa en la figura 9 la visi�n en perspectiva de la geod�sica sobre el cono. All� se ve claramente c�mo la l�nea se acerca al v�rtice hasta una distancia m�nima y posteriormente se aleja de �l. La carga da vueltas en torno al eje de simetr�a del cono con un radio de giro que disminuye al acercarse al v�rtice y aumenta cuando se aleja. El cono act�a como un espejo magn�tico e ilustra este fen�meno.
H. Poincar� (1854-1912) encontr� por primera vez en 1896 la descripci�n matem�tica del movimiento de una carga en el campo del monopolo. La soluci�n matem�tica de saber c�mo se mueve una carga en un campo de monopolo la us� Poincar� para explicar el comportamiento de un chorro de electrones, reflej�ndose violentamente, sobre la punta de un im�n.
Por otra parte, esta imagen tan simple de los espejos magn�ticos no se encuentra en la realidad porque no abundan en la naturaleza los monopolos magn�ticos o no los hemos sabido contemplar. Algunos f�sicos experimentales como B. Cabrera creen haber observado a uno de estos monopolos, pero uno no es suficiente para convencer a los cient�ficos esc�pticos (V�ase en esta serie el libro La gran ilusi�n, 1, El monopolo magn�tico, donde Jorge Flores escribe sobre este descubrimiento).
Con esta descripci�n del movimiento de las cargas ante el influjo del monopolo no quiero defender su existencia sino explicar los espejos magn�ticos con el ejemplo m�s simple que se conoce.
Los espejos magn�ticos reales tienen sus l�neas del campo curvas, no rectas como las del monopolo. Sin embargo, la imagen de una carga reflej�ndose en un espejo magn�tico puede muy bien ilustrarse con la descripci�n que se ha hecho de la carga que se mueve en un campo de monopolo sobre un cono circular.
El movimiento de las cargas en un campo electromagn�tico dado obedece a una ecuaci�n de movimiento conocida. Conocer la ecuaci�n de movimiento no significa conocer el movimiento autom�ticamente, es preciso realizar un proceso llamado integraci�n de las ecuaciones de movimiento, mediante el cual se descubre el movimiento a partir de las ecuaciones, por un proceso que puede ser sumamente dif�cil y complejo y llevar a�os de b�squeda y trabajo.
En unos pocos casos excepcionales este proceso se ha llevado a cabo para ciertos campos electromagn�ticos bastante simples, como en el caso del movimiento de una carga en el campo de Coulomb de otra carga, el movimiento en el interior de un campo constante, o el movimiento en el campo de monopolo. En general, sin embargo, no se ha sabido integrar las ecuaciones de movimiento, lo que en pocas palabras significa que no se sabe a�n c�mo se mueven las cargas. Se conocen algunas propiedades generales del movimiento, pero se desconoce en general su comportamiento.
AURORAS POLARES

Un ejemplo de movimiento en un campo, cuyo estudio lleva muchos a�os, es el movimiento de una carga en el campo de un dipolo magn�tico. Este estudio es importante debido a que la Tierra tiene un campo magn�tico que se parece a un dipolo. El campo de la Tierra es m�s complicado que el campo de un dipolo, pero el campo m�s sencillo que tiene mayor parecido al campo de la Tierra es el campo dipolar.
El campo dipolar parece bastante sencillo y sin embargo integrar las ecuaciones del movimiento de una carga en este campo parece una proeza imposible. St�rmer (1874-1957) fue uno de los primeros investigadores en enfrentar directamente el problema de la integraci�n de las ecuaciones de movimiento, lo cual motiv� que muchas personas lo llamen "el problema de St�rmer". Para �l, este problema pod�a dar una explicaci�n al fen�meno conocido como auroras polares. Aunque St�rmer haya integrado las ecuaciones de movimiento en s�lo unos casos particulares, la mayor�a de los investigadores est� de acuerdo en que las auroras polares se producen como consecuencia del movimiento de cargas en el campo magn�tico de la Tierra.
Algunos a�os despu�s de esos estudios de St�rmer, se descubri� el efecto de latitud de los rayos c�smicos. Este efecto es tambi�n explicado por el movimiento de cargas en el campo magn�tico de la Tierra; de nuevo se volvi� importante la integraci�n de las ecuaciones de movimiento. Durante muchos a�os, Manuel Sandoval Vallarta (1899-1977) y Georges Lemaitre estudiaron este problema. M�s recientemente, al descubrirse los cinturones Van Allen en 1958, se volvi� a poner de moda este problema.
Pasemos revista de estos fen�menos interesantes y veamos tambi�n el origen de que se mantengan sin resolver durante muchos decenios ciertos problemas de tipo cient�fico.
Hablemos un poco de las auroras polares, algunas veces llamadas auroras boreales por quienes las observaron en las regiones n�rdicas de nuestro planeta, sin darse cuenta que son igualmente frecuentes en las regiones australes. Como su nombre lo indica, son fen�menos luminosos que se observan con mayor frecuencia en las regiones m�s alejadas del ecuador terrestre. El cielo se inunda de luces extraordinarias de colorido variable que se observan simult�neamente en lugares distantes m�s de mil kil�metros alrededor del casquete polar. El horizonte se ti�e de luces como si hubiera en la cercan�a un incendio enorme. En las regiones tropicales del planeta, estos fen�menos son raramente observables, y mucho menos con la intensidad y belleza con que se observan en las partes mas fr�as del globo terr�queo.
Estos meteoros presentan formas muy diversas, desde una d�bil luminosidad hasta alcanzar brillos que compiten con el resplandor de las estrellas. Se forman manchas parecidas a nubes, fajas largas en movimiento, arcos homog�neos y arcos separados por estr�as oscuras. Llega a observarse rayos independientes formando una guirnalda en la direcci�n del polo superior de la br�jula de inclinaci�n. Pueden ser rayos independientes formando, a base de curvas onduladas, una gran corona polar.

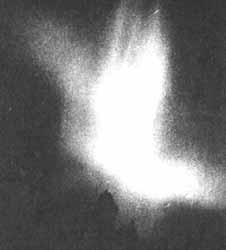
Figura 11. Aurora polar, tomada de El redescubrimiento de la Tierra, CONACYT.

Las auroras polares se explican por la acci�n de cargas el�ctricas sobre la atm�sfera. El campo magn�tico de la Tierra forma una coraza que generalmente no pueden atravesar dichas cargas, las cuales quedan atrapadas en un movimiento continuo de vaiv�n entre las l�neas del campo, rebotando en las regiones polares que act�an como espejos magn�ticos y girando alrededor de las l�neas entre los rebotes de las regiones polares. Pero en algunos casos las cargas se acercan con mucha velocidad a los polos magn�ticos y �stos no las pueden reflejar. As� penetran en la atm�sfera, y al chocar contra las part�culas que la forman se producen radiaciones. �stas tienen lugar en la ion�sfera cuando las cargas intrusas chocan contra iones de ox�geno y nitr�geno y se libera energ�a en forma luminosa. Luces azules y violetas del nitr�geno, luces rojas, amarillas y verdosas del ox�geno, con s�bitas variaciones de color e intensidad. Si el n�mero de cargas energ�ticas es abundante, el fen�meno es f�cilmente observable como un espect�culo luminoso.
Las auroras aparecen simult�neamente en los dos hemisferios de la Tierra y ocurren con mayor frecuencia e intensidad un d�a despu�s de haberse observado perturbaciones magn�ticas en forma de protuberancias en la parte visible del disco solar. Son m�s frecuentes en primavera y oto�o, cuando el ecuador geomagn�tico coincide casi con el plano de la �rbita de la Tierra. La ocurrencia de las auroras polares se acompa�a de tormentas magn�ticas observables por la perturbaci�n de las comunicaciones inal�mbricas. Su intensidad y frecuencia est�n correlacionadas con el ciclo de once a�os, que tambi�n se observa en las manchas del Sol. Este ciclo de once a�os no ha existido siempre en el Sol, y se desconocen las causas tanto de su periodicidad actual como de su ausencia en �pocas pasadas.
La relaci�n de tormentas y auroras fue observada por Celsius en 1741. El sueco Wilcke encontr� en 1770 en Estocolmo que los rayos observados en las auroras boreales siguen la direcci�n de las l�neas magn�ticas de la Tierra. Entre 1826 y 1856, S. H. Schwabe, boticario de Dassau, Alemania, convenci� al mundo con sus observaciones sobre el ciclo de once a�os para la aparici�n de manchas en la superficie del Sol. Este ciclo solar descubierto por Schwabe fue popularizado por el libro titulado Cosmos, del bar�n Von Humboldt. En 1852, varios autores dieron parte de la relaci�n entre el periodo del ciclo solar y el de las mayores perturbaciones magn�ticas, estableciendo emp�ricamente su correlaci�n.
Las auroras polares, los cinturones de Van Allen —que despu�s describiremos— y muchos otros fen�menos geof�sicos de nuestro planeta se originan en el viento solar.
El viento solar se descubre en 1951 cuando el astrof�sico alem�n Ludwig Biermann explica la posici�n relativa de la cola de los cometas en relaci�n a esta hip�tesis. Seg�n la teor�a de E. N. Parker de 1958, el viento solar se origina en la corona solar como consecuencia de las muy altas temperaturas que provocan velocidades cercanas a 150 km por segundo para los protones y 30 veces m�s para los electrones. Con estas velocidades, a cierta distancia del centro solar, deja de ser suficiente la atracci�n gravitacional del Sol y los electrones escapan del Sol, y al escapar atraen consigo a los protones vecinos, se produce entonces dicho viento con velocidades mayores a los 400 km por segundo. La densidad del viento disminuye de un mill�n de millones de part�culas por cent�metro c�bico al nivel de la corona solar, a �nicamente 10 part�culas por cent�metro c�bico al llegar a la Tierra. La velocidad no se modifica mucho durante el trayecto, pero la densidad se va repartiendo cada vez en una mayor �rea y decrece con el cuadrado de la distancia.
Las nuevas teor�as atribuyen el origen del viento solar a las regiones cercanas a los polos magn�ticos, su medici�n no se hab�a realizado porque s�lo a finales de 1986 se lanz� la primera sonda espacial fuera del plano de la el�ptica que contiene a los planetas y al ecuador solar. La espiral de Arqu�medes que se forma al seguir el viento solar al campo magn�tico del Sol en rotaci�n, no es, como se cre�a, un fen�meno cercano al plano de la el�ptica, sino un fen�meno tridimensional en forma de un list�n de tela puesto en rotaci�n por una gimnasta o una bailarina.

Figura 12. Los cuatro soles, centro del llamado Calendario Azteca.

Una propiedad extraordinaria del viento solar es la de ser un conductor el�ctrico perfecto. El campo magn�tico que acompa�a su corriente viaja con �l y produce un efecto colectivo en el viento, aun a bajas densidades, donde las propiedades de fluido parecer�an no existir. Mediciones indirectas hacen pensar en el plasma del viento solar como un fluido turbulento, donde las cargas interaccionan por medio de ondas de plasma dependientes de la temperatura.
Cuando el Sol aumenta su actividad con tempestades de plasma, hay r�fagas solares y enormes explosiones que env�an al sistema planetario olas gigantes de plasma que superan de dos a cinco veces la velocidad habitual del viento solar. Estas ondas r�pidas alcanzan a las de menor velocidad e igual que en otros fen�menos ondulatorios, aparecen las ondas de choque, con dos velocidades diferentes, como cuando un avi�n rompe la barrera del sonido.
Existe una discontinuidad en el campo magn�tico de la Tierra, la cual es tambi�n una onda de choque entre el campo magn�tico de la Tierra y el viento solar desviado por la presencia del dipolo terrestre. El viento solar se desv�a rodeando las superficies de campo constante, no pudiendo acercarse m�s de unos 10 a 15 radios terrestres del lado del Sol. Del lado opuesto al Sol, el viento solar forma una cauda enorme y alargada que deja en el espacio, al alejarse de la Tierra, su huella en la forma de una gran estela. Se forma as� una c�psula geomagn�tica en forma de cometa, donde queda encerrado el campo magn�tico de tipo dipolar.
El grueso de la cola magn�tica de la Tierra oscila entre cuarenta y sesenta radios terrestres, y su longitud se extiende a grandes distancias, m�s de mil radios de la Tierra. La parte norte de la cola est� magnetizada en forma diferente que la parte sur. Mientras que en la mitad norte las l�neas del campo se alejan de la Tierra apuntando hacia el Sol, en la mitad sur las l�neas del campo magn�tico se alejan de la Tierra apuntando en el mismo sentido en que se aleja.
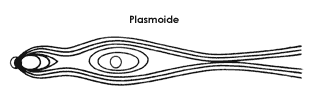
En presencia de tormentas magn�ticas, se han observado fen�menos especiales originados dentro de la cauda de la Tierra. Cuando la cauda de la Tierra est� muy grande y energ�tica, se desprende de la Tierra una enorme masa de plasma en direcci�n de la estela, con sus extremos puntiagudos hacia la Tierra y hacia el exterior, y con su panza gorda. En su centro se hace un torbellino de plasma, cuyo eje se genera a unos cincuenta radios terrestres y se desplaza hacia el extremo de la cola con una velocidad de entre 500 km y 1 000 km por segundo. Estos proyectiles de plasma son llamados plasmoides, y han sido medidos por sat�lite y producidos en los laboratorios. Los plasmoides se han producido experimentalmente como uno m�s de los esfuerzos destinados a obtener en la Tierra el control de las reacciones de fusi�n.
Al ocurrir las tormentas magn�ticas producidas por el incremento de la actividad solar, la c�psula geomagn�tica se comprime, y las comunicaciones de radio y televisi�n se afectan por tormentas magn�ticas. Simult�neamente, se embellece el cielo con brillantes auroras polares.
En los polos, las noches sin auroras son excepcionales aunque con diferentes grados de intensidad. Conforme se aleja uno de los polos, la frecuencia de observaci�n disminuye.
Las auroras polares, en otros planetas como J�piter y Saturno, se han observado con ayuda de sondas espaciales enviadas al espacio para obtener informaci�n cient�fica. Estas auroras son a�n m�s espectaculares que en la Tierra, principalmente en J�piter, donde los meteoros luminosos se extienden por miles de kil�metros en todas direcciones alrededor de los polos magn�ticos del planeta.
Las caudas de los otros planetas, producidas por el viento solar, se han observado asimismo bajo una forma caracter�stica en cada planeta, seg�n la naturaleza del campo magn�tico. Los planetas con campo magn�tico son protegidos del ataque directo del viento solar, el cual se curva en torno al campo magn�tico, formando la magnet�sfera, y rodea al planeta. Los planetas con un campo magn�tico menor, como Venus, reciben directamente la agresi�n del viento solar, pero poseen tambi�n una cauda m�s delgada que se extiende en el espacio.

Figura 13. Plasmoides.

Los cometas se entienden mejor ahora cuando se considera la cauda formada principalmente por el viento solar y apuntando siempre en contra del Sol. Algunos autores distinguen tambi�n otra componente propia del cometa en la cauda, pero la importancia del viento solar en la explicaci�n de la cauda cometaria es definitiva.
LOS RAYOS C�SMICOS

Los rayos c�smicos son part�culas cargadas de gran energ�a que en un principio fueron observadas por su acci�n ionizante en el aire. Los materiales radiactivos producen la ionizaci�n de la atm�sfera vecina. Con el tiempo, se detect� otro tipo de ionizaci�n diferente de aquella producida en la vecindad de los materiales radiactivos.
El origen de los rayos c�smicos no est� esclarecido del todo. Existen rayos c�smicos que se originan en el Sol, pero hay otros cuyo origen es ajeno al sistema solar. Para algunos autores estos rayos c�smicos provenientes del exterior pueden crearse por interacci�n de los restos de las supernovas con c�mulos de estrellas azules j�venes conocidas como asociaciones OB.
El sat�lite C0S-B, de la Agencia Espacial Europea, ha detectado fuentes de rayos gamma que est�n en la misma regi�n del espacio que los c�mulos OB. Se sabe que las supernovas no son en s� fuentes probables de rayos gamma y �stos parecen provenir de objetos j�venes. Si una supernova est� rodeada por c�mulos de estrellas azules, el gas que resulta de la explosi�n acelerar�a las part�culas de baja energ�a que existan en las estrellas azules vecinas hasta el nivel donde se forman los rayos c�smicos y se producir�a la radiaci�n gamma.
Otras muy interesantes hip�tesis se han propuesto para explicar el nacimiento y procedencia de los rayos c�smicos, los cuales son part�culas cargadas de gran energ�a. Las energ�as de algunos de �stos son tan altas que no se podr�an obtener de ninguna reacci�n nuclear conocida. Se especula que adquieren su energ�a en alg�n proceso electromagn�tico que las bombea hasta que alcanzan grandes velocidades.
Desde sat�lites enviados por el hombre se han podido observar los rayos c�smicos fuera de la acci�n del campo geomagn�tico. El Sol emite en forma continua rayos c�smicos de baja energ�a, pero durante las r�fagas solares el Sol lanza al sistema planetario rayos c�smicos de enorme energ�a. Esta radiaci�n no se encuentra en todas direcciones sino que elige como direcciones preferentes las de la espiral de Arqu�medes.
La espiral de Arqu�medes tiene su origen en el campo fotosf�rico del Sol. Cuando es transportado por el viento solar, arrastrado y alargado radialmente, toma una forma espiral debido a la rotaci�n solar y se extiende por el medio interplanetario formando un campo magn�tico que en �pocas de baja actividad solar muestra cuatro sectores con polaridad alterna que los planetas barren al girar con una velocidad angular de aproximadamente una vuelta cada mes, correspondiente al periodo de rotaci�n de 27 d�as del Sol.
La radiaci�n c�smica gal�ctica puede distinguirse por ser de mayor energ�a por part�cula que la originada en el Sol y por aumentar su densidad en direcciones diferentes de la direcci�n solar. La radiaci�n gal�ctica se dispersa por las irregularidades del campo que viaja hacia ella. El viento solar tiende a barrerla en contra de la direcci�n del Sol, pero este efecto es menor para part�culas de alta energ�a y en periodos de poca actividad solar.
La radiaci�n c�smica posee un enorme poder de ionizaci�n, por lo cual se pens� originalmente en una radiaci�n formada por rayos gamma. Se le llama radiaci�n gamma a los rayos electromagn�ticos de gran frecuencia y gran energ�a, observados primero como emanaciones radiactivas con gran poder ionizador. Los materiales radiactivos emiten dicha radiaci�n con la posibilidad de ser detectada despu�s de tener una colisi�n el�stica con electrones. Si los rayos c�smicos fueran radiaci�n gamma, entonces ser�an f�sicamente observables despu�s de chocar con electrones y producir ionizaci�n y otros fen�menos electromagn�ticos. Posteriormente veremos que esto no es as�, los rayos c�smicos son cargas el�ctricas que se mueven a gran velocidad.
El hombre puede obtener part�culas altamente energ�ticas en los laboratorios por medio de aceleradores de part�culas. Las part�culas de mayor energ�a producidas en el laboratorio tienen miles de millones de electr�n-voltios. La mayor�a de los rayos c�smicos que llegan a la Tierra tienen energ�as de este orden de magnitud, sin embargo muchos de ellos pueden tener un mill�n de veces m�s energ�a. Incluso pueden encontrarse algunos que poseen energ�as mil millones de veces mayores que las producidas en los grandes aceleradores.
En la radiaci�n c�smica se distinguen la primaria de la secundaria; ll�mase primaria a aquella que proviene del exterior de la Tierra, secundaria a la producida como consecuencia de las colisiones que sufre la primera con part�culas que se encuentran en la atm�sfera terrestre.
En 1901 Ch. T. R. Wilson (1869-1959) en Inglaterra y J. Elster (1854-1920) y H. Geitel (1855-1923) en Alemania, observaron que si se deja aire en reposo en un recipiente cerrado herm�ticamente y libre de polvo, �ste se ioniza ligeramente al paso del tiempo. La rapidez de ionizaci�n producida es proporcional al volumen y a la presi�n. En 1903, E. Rutherford (1871-1937) y Cooke en Inglaterra y Mc Lennan y Burton en Montreal informaron que esta ionizaci�n del aire se ve reducida al rodearse al recipiente con una capa de unas dos pulgadas de plomo.
Las primeras mediciones de la radiaci�n c�smica en globo las realizaron K. Berwitz en 1909 y A. Gockel en l910 y 1911.
El efecto de la radiactividad disminuye al alejarse de la Tierra. La ionizaci�n puede aumentar al ascender en globo, demostrando otra causa de ionizaci�n diferente a la causada por la radiactividad. En 1912 V�ctor Hess (1883-1964) subi� en globo por siete ocasiones diferentes hasta varios kil�metros de altura, encontrando una ionizaci�n que se incrementaba con el nivel de ascenci�n. En 1936 se le confiri� el premio Nobel a este f�sico austriaco por sus estudios de la radiactividad de la atm�sfera y sus descubrimientos sobre los rayos c�smicos.
Los experimentos, repetidos por W. Kolh�rster (1887-1946) en 1913 y 1914, encontraron a 9 300 metros de altura una rapidez de ionizaci�n 80 veces mayor que la que �l midi� al nivel del mar.
Discrepancias en sus medidas, comunicadas por Millikan (1868-1953) y Bowen en 1922, se explicaron a�os m�s tarde por medio del efecto de latitud.
Los rayos c�smicos fueron observados con ayuda de contadores Geiger-M�ller y c�maras de burbujas por D. Skobelzyn en la ciudad de Leningrado, en 1922. En la c�mara de burbujas los electrones siguen trayectorias casi rectas debido a su alta energ�a. Los investigadores W. Bothe y W. Kolh�rster registraron dos descargas simult�neas en dos contadores superpuestos, aunque se colocara una l�mina de oro de 4 mil�metros de grueso separando a ambos contadores.
B. Rossi observ� m�s tarde que los rayos m�s energ�ticos atravesaban no s�lo 4 mm de oro, sino que podr�an atravesar tambi�n un muro de plomo de un metro de espesor.
En 1927 Jacob Clay, en un viaje mar�timo entre la isla de Java y Holanda, encuentra que la densidad de la radiaci�n c�smica aumenta al acercarse a los polos. En 1928 inform� que, al nivel del mar, la radiaci�n c�smica medida en el ecuador es 10% menor que la medida a 40 grados de latitud norte o sur. En 1930 dio a conocer que el incremento de ionizaci�n con la altura disminuye para latitudes menores. Los trabajos de Clay no fueron aceptados de inmediato porque se trataba de mediciones realizadas sobre embarcaciones sujetas a fuertes movimientos, lo que hac�a dudosas las conclusiones obtenidas. Adem�s, las planchas met�licas de la estructura afectaban las mediciones en forma discutible. La controversia mayor se originaba con Robert A. Millikan, gran investigador experimental que midi� la carga del electr�n. El profesor Millikan estaba convencido de que los rayos c�smicos eran una radiaci�n electromagn�tica similar a la de la luz, pero de mayor energ�a y frecuencia. Basaba su argumentaci�n en que el campo magn�tico de la Tierra parec�a no afectar la intensidad de la radiaci�n. Sin embargo, esta conclusi�n fue obtenida por Millikan como consecuencia de mediciones llevadas a cabo por �l al norte de los Estados Unidos y en el Canad�. Posteriormente se supo que el efecto del campo magn�tico de la Tierra no se percibe a esas latitudes, donde es pr�cticamente constante; el efecto de latitud del campo sobre los rayos c�smicos se percibe claramente mucho m�s al sur, a partir de California.
Como consecuencia del A�o Geof�sico Internacional de 1932 se intensificaron los estudios sobre esta materia y Arthur Compton corrobor� estos resultados y el descubrimiento del efecto de latitud de la radiaci�n c�smica, lo cual prueba el car�cter corpuscular el�ctrico de esta radiaci�n formada por cargas, en contra de la hip�tesis de Millikan, quien sosten�a que la radiaci�n c�smica deber�a estar formada por rayos gamma. Los rayos c�smicos son menos intensos cerca del ecuador que en las zonas templadas o polares. En las regiones polares, el bombardeo de rayos c�smicos es 15% m�s intenso que en el ecuador. La mayor parte del cambio ocurre entre los 20 grados y los 45 grados de latitud. Con la altura, estas diferencias se distinguen mejor. La intensidad a 49 grados es 33% mayor que en el ecuador si se hacen las mediciones a 4 500 metros de altitud. A 65 grados el aumento ser� 65% mayor, a la misma altura.
Una serie de experimentos decisivos en favor de la hip�tesis corpuscular se llev� a cabo cuando se pens� en una diferencia de densidad de carga positiva o negativa en la radiaci�n c�smica. Si la radiaci�n est� formada por una mayor�a de cargas el�ctricas positivas, la radiaci�n ser� mayor del lado Oeste y, viceversa, ganar� la direcci�n Este si la radiaci�n resultara en su mayor parte negativa. Esta predicci�n resulta de la diferencia de comportamiento de las cargas el�ctricas positivas al girar alrededor de las l�neas del campo magn�tico, puesto que giran en direcciones opuestas.
El experimento se llev� a cabo en diversos lugares del mundo, debido al entusiasmo de Arthur Compton, y en M�xico fue realizado por el gran f�sico experimental norteamericano Louis �lvarez, en un cuartel militar del volc�n Nevado de Toluca, a unos kil�metros de la ciudad del mismo nombre; en las ciudades de Orizaba y Veracruz, y en el Hotel G�nova de la ciudad de M�xico, en el mes de agosto de 1932. Como resultado, �lvarez encontr� una mayor intensidad en los rayos procedentes del Oeste, comparada con aqu�lla viniendo del Este. Esta preferencia anuncia que los rayos medidos, afectados por el campo magn�tico de la Tierra, son en su mayor parte cargas el�ctricas positivas.
Las mediciones en la cumbre del Nevado de Toluca pudieron efectuarse debido a los buenos oficios del profesor Manuel Sandoval Vallarta, quien estaba de vacaciones de verano en M�xico. Sandoval Vallarta no s�lo ayud� con su hospitalidad a realizar estas mediciones, sino que tambi�n se contagi� con la importancia del descubrimiento y principi� a trabajar los aspectos te�ricos y matem�ticos de este resultado con su compa�ero de estudios G. Lemaître.
Recordemos la descripci�n que hace don Manuel Sandoval Vallarta de la experiencia de �lvarez:

En la azotea del Hotel G�nova, en M�xico, coloc� una caja de madera y en la tapa de esta caja estaban sujetos dos contadores Geiger. Primero fij� la posici�n de la caja a �ngulo fijo, despu�s puso todo sobre una carretilla, e hizo girar la carretilla de manera que primero midiera de lado Oriente y despu�s el lado Occidente. El resultado fue que la intensidad del Occidente era mayor que la del Oriente, y por consiguiente la radiaci�n que llega a la Tierra era predominantemente positiva.

Compton no solo realiz� sus experiencias en M�xico, sino tambi�n convenci� a Sandoval Vallarta a enfrentar el problema de la interpretaci�n te�rica de la din�mica de la radiaci�n c�smica en el campo dipolar de la Tierra.
EL PROBLEMA DE ST�RMER

Como se dijo al principio de este cap�tulo, el estudio del movimiento de una carga en un campo dipolar fue iniciado por el cient�fico sueco St�rmer.
St�rmer y sus ayudantes calcularon a mano muchas trayectorias de las cargas en el campo dipolar por diversos m�todos num�ricos, algunos de los cuales fueron inventados por �l para resolver ese problema y se contin�an usando en la actualidad.
El movimiento de una carga en el campo dipolar es uno de los problemas m�s interesantes de la f�sica matem�tica. A primera vista, no se ve m�s dif�cil que tantos otros, resueltos con ayuda de funciones del tiempo. Conforme uno profundiza en tratar de obtener la soluci�n que se conoce como integrar las ecuaciones de movimiento, pronto se descubre que se trata de uno de los problemas llamados ca�ticos debido a su complejidad, y se llama tambi�n no integrable en vista de su dificultad.

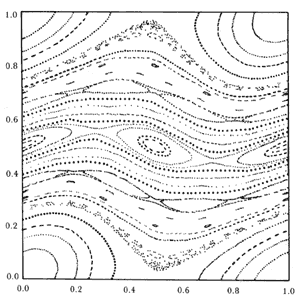
Figura 14. Diagrama t�pico de la intersecci�n de las trayectorias de un sistema no integrable
con un plano fijo.

Para dar al lector una idea de lo que se entiende con estas expresiones en la figura 14 se presenta un diagrama t�pico de la intersecci�n de las trayectorias de un sistema no integrable con un plano fijo. Esta intersecci�n se llama Secci�n de Poincar� porque este matem�tico recomend� dichas intersecciones para el an�lisis te�rico del movimiento. Se nota en dicha figura nubes de puntos alrededor de ciertas islas de forma el�ptica, cuyo centro est� formado siempre por trayectorias peri�dicas estables. Estas islas est�n separadas por nubes de puntos que forman dos equis a ambos lados de las islas. El punto de cruce de la equis es tambi�n una trayectoria peri�dica pero inestable. En una trayectoria vecina de la peri�dica inestable la carga se mueve alej�ndose de dicha �rbita inestable pero limitada siempre por las dos l�neas de la equis que se parecen a las dos rectas as�ntotas de la curva hip�rbola. La hip�rbola se acerca a sus as�ntotas, sin poderlas alcanzar jam�s. Conocida una �rbita peri�dica, el estudio del movimiento de una �rbita vecina permite conocer la estabilidad de esa trayectoria peri�dica y predecir el tipo de comportamiento de cualquier otra �rbita de la vecindad.
Para tener una idea del tipo de trayectorias que se encuentran en presencia de un campo magn�tico, puede tomarse un alambre muy flexible por el que pasa una corriente el�ctrica, y se coloca en presencia de un im�n. El alambre toma entonces la forma de las trayectorias de las cargas en presencia de ese im�n. Esta experiencia fue llevada a cabo por Weyr; posteriormente Graef y Kusaka confirmaron con c�lculos la forma obtenida experimentalmente por Weyr.
Las trayectorias peri�dicas forman en el espacio curvas cerradas que pueden generar figuras de rosetas con varios p�talos. Las trayectorias pueden enredarse para formar nudos de complejidad insospechada, dependiendo del campo magn�tico que las produce.
El c�lculo de las trayectorias de las cargas por m�todos num�ricos se facilit� con la llegada de las computadoras. La primera computadora usada en este problema es hoy una antig�edad venerable. Se trata de la m�quina del ingeniero V. Bush, que ocupaba todo un sal�n en el Instituto Tecnol�gico de Massachusetts. La m�quina integraba num�ricamente las trayectorias utilizando la velocidad angular de discos de vidrios y bronce que giraban y comunicaban su velocidad por fricci�n a otros discos. Los ejes de rotaci�n de los discos puestos en contacto eran perpendiculares. Los cambios en la velocidad angular se obten�an acercando la circunferencia del disco movido, a un punto m�s cerca del eje de rotaci�n del disco impulsor. Los discos esmerilados de vidrio rotaban con su eje vertical, y los discos de bronce, de circunferencia menor, rotaban en ejes horizontales, mismos que pod�an acercarse y alejarse del eje vertical, cambiando por eso su velocidad angular. Se calcularon con esta m�quina muchas trayectorias, y los resultados de algunas de ellas fueron confirmados con c�lculos hechos manualmente.
El integrador diferencial de V. Bush se puso al servicio de integrar las ecuaciones de movimiento del problema de St�rmer. Cada integraci�n num�rica de una trayectoria cambia con la selecci�n de las condiciones iniciales, las cuales pueden elegirse en una cantidad infinita de formas diferentes. La informaci�n de un integrador num�rico es relativa en su utilidad. Puede ser muy �til cuando se puede inferir de los ejemplos calculados una idea mediante un proceso de s�ntesis. Cuando las soluciones num�ricas s�lo sugieren semejanzas con el caos, el estudio de las soluciones no ha terminado.
Don Manuel Sandoval Vallarta, como profesor del Instituto Tecnol�gico de Massachusetts, dirigi� muchos trabajos de investigaci�n sobre este problema. Manuel Sandoval Vallarta naci� en febrero de 1899 y se educ� en la Escuela Nacional Preparatoria, que fue una excelente formadora de alumnos bien preparados. En 1917 viaj� a Estados Unidos para iniciar sus estudios profesionales en el Instituto Tecnol�gico de Massachusetts. En 1926, despu�s de completar su formaci�n en Europa, fue nombrado profesor adjunto de f�sica en el mismo Instituto, donde prosigui� su carrera cient�fica hasta 1946, a�o en que deja su puesto de profesor titular para regresar a M�xico. Sandoval Vallarta tomaba sus vacaciones en M�xico y aprovechaba sus viajes para comunicar los avances de la ciencia en los seminarios de la Sociedad Cient�fica Antonio Alzate, organizados por don Sotero Prieto. Sandoval Vallarta ten�a en Massachusetts excelentes alumnos. Dos de ellos fueron Reina Albagli Hutner y E. J. Shremp. Don Manuel convenci� a algunos brillantes estudiantes mexicanos para que siguieran la carrera cient�fica en el Instituto donde �l trabajaba.

Figura 15. Manuel Sandoval Vallarta y su esposa Mar�a Luisa Margain.

A. Ba�os fue disc�pulo suyo; despu�s de trabajar con �l en el problema de St�rmer vino a M�xico y fue el primer director del Instituto de F�sica de la Universidad Nacional Aut�noma de M�xico, en 1939. Estudi� las �rbitas asint�ticas de �rbitas peri�dicas, es decir las trayectorias que se van acercando, al pasar el tiempo, a una �rbita peri�dica. Form� un peque�o grupo de investigaci�n con Jaime Lifshitz, H�ctor Uribe y Juan Oyarz�bal con el prop�sito de estudiar este problema. Posteriormente, regres� a los Estados Unidos, donde se distingui� por sus estudios en la magnetohidrodin�mica, la ciencia dedicada al estudio del movimiento de los plasmas. Escribi� un trabajo muy importante donde obtuvo un m�todo simple para escribir el movimiento del centro gu�a. Ba�os volvi� a M�xico a principios de los sesentas y fue entonces el primer director del Departamento de F�sica del Centro de Investigaci�n y Estudios Avanzados del Instituto Polit�cnico Nacional, otro centro de excelencia de la investigaci�n en M�xico. Jaime Lifshitz public� con G. D. Birkhoff un trabajo en una revista de Argentina sobre problemas mec�nicos sin trayectorias peri�dicas y en M�xico prosigui� su investigaci�n sobre rayos c�smicos.
El doctor Carlos Graef Fern�ndez fue otro de los disc�pulos de Manuel Sandoval Vallarta. En un trabajo publicado por �l con Kusaka, ambos integraron las trayectorias de las cargas que se mueven en el plano ecuatorial del dipolo con ayuda de funciones peri�dicas del tiempo. Estas funciones son las mismas que predicen el movimiento de un p�ndulo o la rotaci�n de un cuerpo asim�trico. En el caso del dipolo se encontraron trayectorias con un movimiento peri�dico en forma de roseta. V�ase en la figura 16 la trayectoria obtenida recientemente con una computadora de uso com�n y corriente en muchas oficinas de nuestras universidades. Jaime Lifshitz determin� cu�les de esas �rbitas eran estables.

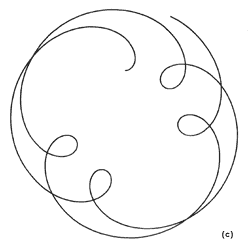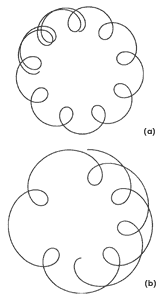
Figura 16. (a), (b) y (c) Trayectorias de cargas en forma de roseta con movimiento peri�dico. Se obtuvieron con una computadora.

En 1935 Compton y Getting predijeron una variaci�n de la intensidad de la radiaci�n c�smica en funci�n de la posici�n relativa de las estrellas, en el caso de que las part�culas que constituyen la radiaci�n c�smica primaria provinieran del exterior de la V�a L�ctea. Este efecto era consecuencia de la rotaci�n de la galaxia. En 1939 Graef Fern�ndez, Kusaka y Sandoval Vallarta analizaron el efecto de rotaci�n de la galaxia para las part�culas que caen verticalmente en el ecuador y encontraron que si se toma en cuenta el campo magn�tico de la Tierra, no se puede conocer de esta forma si las cargas son de origen extragal�ctico.
El doctor Carlos Graef Fern�ndez present� una tesis, la cual le fue dirigida por Sandoval Vallarta; all� desarrolla un estudio de �rbitas peri�dicas del movimiento de cargas en el campo dipolar. Demostr� que las �rbitas deben cortar al ecuador del dipolo, y que es posible usar el ecuador como un registro del paso de las cargas. Si el movimiento es peri�dico, la carga pasar� despu�s de alg�n tiempo por el mismo punto de intersecci�n del ecuador. El estudio del doctor Graef fue muy importante por el an�lisis de los diversos tipos de movimientos que se pueden dar en relaci�n con este problema. Aunque dicho trabajo fue de tipo cualitativo, es a�n un gran avance insuperado en este ejemplo de mec�nica y una fuente de inspiraci�n de otros tan complejos como el de St�rmer.
Al mismo tiempo que el profesor Sandoval Vallarta formaba alumnos en el Instituto Tecnol�gico de Massachusetts para atacar el problema de St�rmer, en Lovaina, B�lgica, Lema�tre continuaba tambi�n dicho estudio en colaboraci�n con el anterior. Destac� entre los alumnos m�s brillantes de Lemaître el cient�fico belga Othon Godart, quien se preocup� por determinar la estabilidad de las �rbitas peri�dicas en respuesta a la pregunta: �Se mueve la �rbita vecina de una trayectoria peri�dica siempre en la vecindad de esa trayectoria, en forma estable, o se aleja incesantemente de ella, y es entonces inestable? Otro alumno proveniente de B�lgica es Bouckaert, quien trabaj� posteriormente en Estados Unidos.
Del estudio sistem�tico de las �rbitas posibles para rayos c�smicos en presencia de un campo dipolar se dedujeron varias superficies que acotaban las regiones donde era posible encontrar a los rayos c�smicos. El cono principal era el conjunto de direcciones permitidas para que cargas viniendo de muy lejos, pero de todas partes, pudieran llegar a un observador. A �ste debe sustraerse el cono de sombra, compuesto por las direcciones permitidas por el campo dipolar que son bloqueadas por la presencia de la Tierra. Asimismo, el cono de penumbra, formado por bandas permitidas y prohibidas. Y el cono prohibido, dentro del cual las cargas que vienen de muy lejos no podr�an alcanzar al observador. Con el tiempo se conoce mejor el campo magn�tico de la Tierra y estas superficies se han tenido que volver a calcular, pero las ideas fundamentales permanecen vigentes.
Al aparecer las computadoras electr�nicas, este problema fue nuevamente atacado con potente capacidad de c�lculo. De Vogelaere, un cient�fico belga, disc�pulo de Othon Godart y radicado en Canad�, pudo hacer uso de las facilidades del National Bureau of Standards, en Washington. La importancia del estudio de De Vogelaere fue la obtenci�n de nuevas fuentes de inspiraci�n para descubrir superficies de simetr�a en relaci�n con este problema, que pod�an numerarse, y tales que el corte de dos superficies de simetr�a diera la posici�n de una �rbita cerrada con tantas vueltas antes de cerrarse, como la diferencia de los dos n�meros de las superficies de simetr�a. Los c�lculos del problema de St�rmer con estas ideas se llevaron a cabo en 1958, cuando en los Estados Unidos se contaba con unas doscientas computadoras.
En nuestros d�as este problema sigue vivo, recibiendo nuevos enfoques y desarrollos. Estudio de otras trayectorias. An�lisis con nuevos m�todos. En M�xico, los estudios de rayos c�smicos y en general de f�sica espacial son dirigidos por Ruth Gall, quien mantuvo la colaboraci�n cient�fica con el profesor Sandoval Vallarta durante muchos a�os. Fuera de M�xico, se han proseguido desarrollando tambi�n los aspectos matem�ticos del problema de St�rmer. Adem�s de los trabajos ya mencionados de De Vogelaere, existe un trabajo sistem�tico llevado a cabo por la escuela griega donde destacan G. Contopoulos, L. Vlahos, V. V. Markellos, S. Klimopoulos y A. A. Halioulias. En relaci�n con el inter�s despertado por los cinturones de radiaci�n de Van Allen, de los cuales se hablar� en el cap�tulo que sigue, se hicieron varios estudios, entre los cuales destacan los de A. Dragt y M. Finn y de T. Northrop y E. Teller. Interesados a�n en este problema encontramos a Gerard Gomes en Barcelona, Luis V�zquez en Madrid, Robert Broucke en Austin y Lidia Jim�nez Lara y Jos� Luis Fern�ndez Chapou en la ciudad de M�xico.