II. C�MO FUNCIONA EL TELESCOPIO

UN TELESCOPIO es esencialmente un par de lentes, una llamada objetivo porque es la m�s cercana al objeto, y otra llamada ocular porque es la m�s cercana al ojo, como se muestra en las figuras 3(a) y 4(a). El objetivo es una lente convergente que forma una imagen I del objeto. Es f�cil comprender que esta imagen es tanto mayor cuanto m�s larga sea su distancia focal, es decir, cuanto menos convergente sea. Esta imagen I se observa despu�s con el auxilio de una peque�a lente, divergente como en el telescopio galileano de la figura 3(a), o convergente como en el telescopio kepleriano de la figura 4(a).

La imagen I, al ser observada, producir� a su vez una imagen en la retina del ojo, que ser� tanto m�s grande cuanto m�s cerca est� esta imagen I del globo ocular. Como el ojo no puede enfocar los objetos que est�n muy cerca de �l, es necesaria la ayuda de una lente, llamada ocular, para realizar este enfoque. Si la imagen I est� atr�s del ojo se usa una lente negativa o divergente, pero si est� adelante se usa una lente positiva o convergente. En vista de esto es f�cil comprender que la amplificaci�n aparente o angular M del telescopio es directamente proporcional a la distancia focal f_ob del objetivo, e inversamente proporcional a la distancia focal f_oc del ocular. Como se puede observar en la figura 4(a), si un objeto tiene un di�metro angular a, la imagen tendr� un di�metro angular b. Si ahora nos damos cuenta de que la lente ocular forma una imagen del objetivo a una distancia l de ella, es f�cil ver que esta relaci�n de �ngulos, o sea la amplificaci�n, est� dada por:

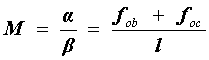(1)

Si ahora usamos una relaci�n muy conocida para determinar la posici�n de la imagen real formada por una lente, que en este caso es el ocular, encontramos:

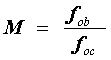(2)

Esta amplificaci�n angular de los di�metros aparentes de los objetos observados se puede interpretar tambi�n como un acercamiento del objeto. As�, con una amplificaci�n de cinco, los objetos se ven a trav�s del telescopio a la quinta parte de su distancia real.

En un telescopio, como en cualquier otro sistema �ptico, el haz luminoso est� limitado en extensi�n lateral por una o m�s de las lentes del sistema. Generalmente es una sola superficie la que limita los rayos y recibe el nombre de pupila del sistema. Un rayo que salga de un punto en el objeto fuera del eje �ptico para llegar al punto imagen correspondiente, pasando por el centro de la pupila, se llama rayo principal. Obviamente, existe un rayo principal para cada punto del objeto.

La pupila de entrada es la posici�n aparente que tiene la pupila real cuando se le observa desde el espacio del objeto. La pupila de salida es la posici�n aparente que tiene la pupila real cuando se le observa desde el espacio del ojo que mira a trav�s del telescopio. Alternativamente, podemos decir que la pupila de entrada es la imagen de la pupila real, formada por los lentes del sistema �ptico que preceden a esta pupila real. An�logamente, la pupila de salida es la imagen de la pupila real, formada por las lentes del sistema que siguen a esta pupila real. Las figuras 3 y 4 muestran las posiciones de estas pupilas para los telescopios galileano y kepleriano. Es f�cil ver que los rayos principales pasan por los centros de las pupilas real, de entrada y de salida.

Es posible demostrar que si el di�metro de la pupila de entrada en un telescopio se representa por dent y el di�metro de la pupila de salida por dsal, la amplificaci�n M estar� dada por

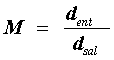(3)

En el telescopio galileano la pupila real o iris puede coincidir sobre el plano del objetivo o sobre el plano de la pupila del ojo del observador, seg�n su amplificaci�n y el di�metro del objetivo. Si el cociente d_ent/M es mucho menor que el di�metro de la pupila del ojo, es decir, si el telescopio tiene un objetivo peque�o y una amplificaci�n grande, la pupila real y la de entrada estar�n sobre el plano del objetivo, como se muestra en la figura 3(a). La pupila de salida no coincide con la del ojo, por lo que el campo visual estar� determinado por el iris del observador.

Si el cociente d_ent/M es mucho mayor que el di�metro de la pupila del ojo, es decir, si el telescopio tiene un objetivo grande y una amplificaci�n peque�a, la pupila real y la de salida estar�n sobre el plano del iris del observador, como se muestra en la figura 3(b). La pupila de entrada no est� en el plano del objetivo, por lo que el di�metro de este �ltimo determina la amplitud del campo visual. Es f�cil ver que el di�metro del objetivo no tiene ninguna relaci�n con el di�metro de la pupila de entrada.

En el telescopio kepleriano, independientemente de su amplificaci�n, las pupilas real y de entrada coinciden con el plano del objetivo y la pupila de salida con el iris del ojo del observador, como se puede ver en la figura 4(a).

LAS ABERRACIONES DE LOS TELESCOPIOS

La calidad de la imagen en un telescopio est� limitada por muchos factores, unos asociados al telescopio mismo, otros al medio en el que se propaga la luz, es decir, a la atm�sfera, y otros que dependen de la naturaleza de la luz.

Describiremos primeramente los que dependen del telescopio y que reciben el nombre de aberraciones. Comenzaremos por recordar que un sistema �ptico ideal, ya sea telescopio o cualquier otro, tiene que refractar los rayos de un punto en el objeto al punto correspondiente en la imagen. Seg�n la posici�n del punto objeto en el campo, y el color de este objeto, podemos clasificar las aberraciones �pticas como sigue:

a) Aberraci�n de esfericidad

b) Aberraci�n de coma

c) Astigmatismo

d) Curvatura de campo

e) Distorsi�n

f) Aberraci�n crom�tica axial

g) Aberraci�n crom�tica lateral

Las primeras cinco aberraciones se pueden manifestar, cualquiera que sea el color del objeto, incluso si es de un color puro, monocrom�tico, por lo que en ocasiones reciben el nombre de aberraciones monocrom�ticas. Las �ltimas dos, en cambio, s�lo pueden aparecer si el objeto es blanco, es decir, si su luz est� formada por la mezcla de muchos colores. A continuaci�n describiremos cada una de estas aberraciones.

Aberraci�n de esfericidad

Supongamos que el punto objeto est� sobre el eje �ptico y que no todos los rayos pasan por el punto imagen en el eje, como se ilustra en la figura 5(a) para una lente y en la figura 5(b) para un espejo. Este defecto es muy frecuente y, debido a que ocurre aun con superficies refractoras de forma esf�rica perfecta, recibe el nombre de aberraci�n de esfericidad. A causa de esta aberraci�n, los rayos reflejados en una superficie esf�rica o cil�ndrica forman una figura caracter�stica, a la que se le da el nombre de c�ustica. Esta se puede observar muy f�cilmente en una taza de caf� iluminada oblicuamente por el sol o por una l�mpara muy intensa.

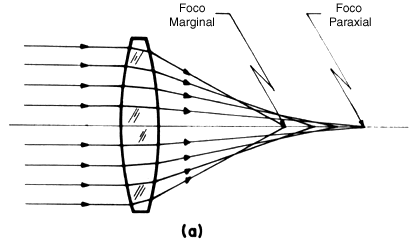
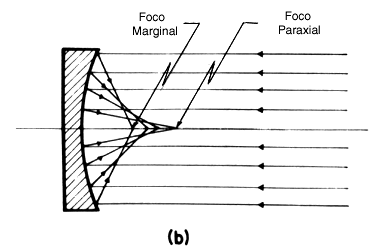
Figura 5. Aberraci�n de esfericidad en el objetivo de un telescopio. (a) Objetivo refractor. (b) Objetivo reflector.

Dada una distancia del objeto, escogiendo de manera adecuada las curvaturas y las formas de las superficies de las lentes, es posible generalmente eliminar esta aberraci�n mediante compensaci�n de las aberraciones introducidas por unas superficies del sistema con las aberraciones introducidas por otras. Por ejemplo, si tenemos una lente convergente simple, pero con una cara convexa y una plana, la orientaci�n que tiene la menor aberraci�n de esfericidad es la que tiene la cara convexa hacia el objeto a una distancia muy grande de la lente, y la cara plana hacia la imagen. Si una lente no tiene corregida su aberraci�n de esfericidad, �sta se puede representar aproximadamente por:

Esf = Aesf D3

(4)

donde A_esf es una constante que depende de c�mo est� construida la lente y de la distancia del objeto a la lente. La magnitud de esta aberraci�n aumenta con el cubo de su di�metro, por lo que la calidad de la imagen aumentar�a dr�sticamente si se reduce la abertura mediante un diafragma, pero esto tiene el gran inconveniente de reducir la cantidad de luz que entra al telescopio.

Un telescopio con aberraci�n de esfericidad tendr�a im�genes borrosas sobre todo el campo, como si estuvieran desenfocadas, y no servir� ning�n esfuerzo por ponerlas en foco. Si los objetos son estrellas, las im�genes son peque�as manchas en lugar de puntos, como se muestra comparativamente en las figuras 6(a) y 6(b).

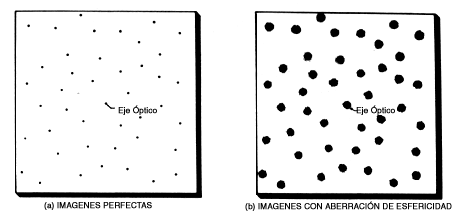
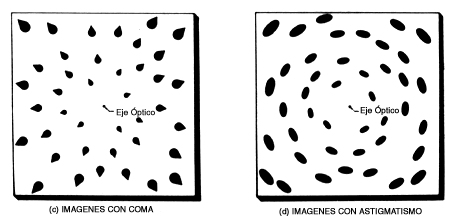
Figura 6. Im�genes estelares en una placa fotogr�fica. (a) Perfectas. (b) Con aberraci�n de esfericidad. (c) Con aberraci�n de coma. (d) Con astigmatismo.

Aberraci�n de coma

Los rayos que se encuentran representados en las figuras 5(a) y 5(b) est�n todos en el plano de la figura, llamado plano tangencial. Al plano perpendicular al tangencial y que contiene el rayo principal se le llama plano sagital. Si el objetivo tiene la aberraci�n llamada coma, no todos los rayos tangenciales llegan a un punto com�n en la imagen, seg�n se ve en la figura 7(a), y la imagen de la estrella, en lugar de ser puntual, tendr� la apariencia de una peque�a coma, como se muestra en la figura 6(c), de donde proviene su nombre. En una lente simple que tenga aberraci�n de coma, �sta se puede representar aproximadamente por:

Coma = Acoma D2 h

(5)

donde A_coma es una constante cuyo valor depende de la configuraci�n de la lente y de la posici�n del objeto. La coma aumenta linealmente con la distancia de la imagen al eje �ptico, por lo que s�lo es perceptible al observar objetos alejados de este eje, cuando el campo es amplio. Por otro lado, la magnitud de la coma tambi�n aumenta con el cuadrado del di�metro de la abertura del telescopio, por lo que al igual que en el caso de la aberraci�n de esfericidad, �sta tambi�n disminuir�a al reducir el di�metro del objetivo.

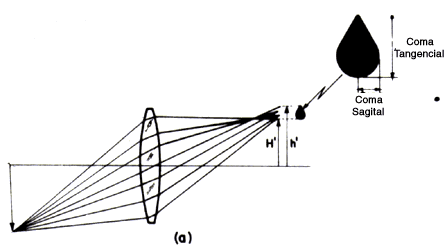
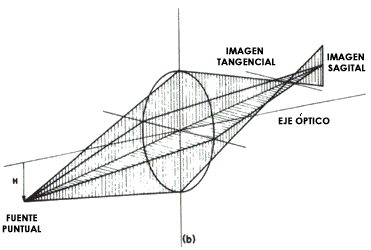
Figura 7. Formaci�n de una imagen puntual fuera del eje �ptico. (a) En la presencia de la aberraci�n de coma. (b) En la presencia de astigmatismo mostrando los focos tangencial y sagital.

Astigmatismo

Desgraciadamente, la ausencia de coma no garantiza de ninguna manera que los rayos en el plano sagital lleguen al mismo punto de los rayos tangenciales. Puede tambi�n suceder que los rayos tangenciales y los sagitales tengan diferente foco, como se ilustra en la figura 7(b), y entonces decimos que el sistema �ptico tiene astigmatismo. Al igual que en el caso de la coma, el efecto es que la imagen es n�tida y clara en el centro del campo, pero tanto m�s difusa y desenfocada cuanto m�s lejos observemos del eje �ptico. Al presentarse el astimagtismo, existen diferentes superficies focales para los rayos sagitales y para los rayos tangenciales. Si el campo visual est� formado por estrellas, las im�genes son circulares o alargadas en la direcci�n radial o tangencial, seg�n la superficie focal que enfoquemos visual o fotogr�ficamente (Figura 8) al hacer la observaci�n, como se muestra en la figura 9(a). La imagen de un circulo con l�neas radiales tendr� las apariencias mostradas en la figura 9(b), seg�n la superficie focal seleccionada. Una placa fotogr�fica del cielo en la presencia de astigmatismo tendr� im�genes estelares como las que se muestran en la figura 6(d). El astigmatismo en una lente simple se puede representar aproximadamente por:

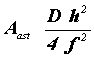(6)

donde A_ast es una constante que depende de la configuraci�n de la lente y de la posici�n del objeto. El astigmatismo crece linealmente con el di�metro del objetivo y con el cuadrado de la distancia de la imagen al eje �ptico. Como en el caso de la coma, esta variaci�n es lineal y el resultado es que para campos relativamente poco amplios la coma es la �nica que se detecta, pero a medida que crece el campo el astigmatismo alcanza a la coma, hasta superarla finalmente. Como en los telescopios el campo no es en general muy grande, la coma es mucho m�s importante de corregir que el astigmatismo. Como se ve en la f�rmula, las distancias focales largas tambi�n reducen el astigmatismo.

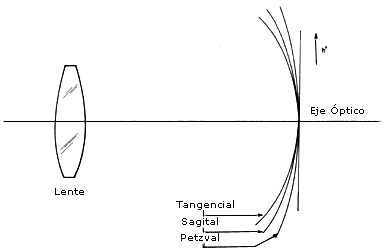
Figura 8. Superficies focales para los planos tangencial, sagital y de Petzval en una lente con astigmatismo. La superficie de Petzval es la superficie focal si la lente no tuviera astigmatismo.

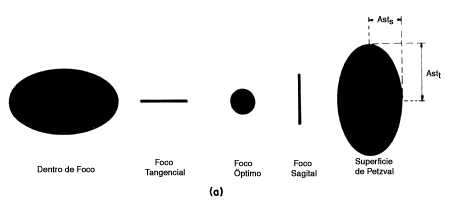
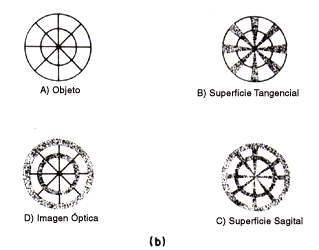
Figura 9. Im�genes en la presencia de astigmatismo. (a) De un objeto puntual. (b) De una circunferencia con l�neas radiales, en las diferentes superficies focales.

Curvatura de campo

Aun en el caso de que todos los rayos que salen de un punto cualquiera en el objeto lleguen a un solo punto sobre la imagen, lo cual sucede si no hay aberraci�n de esfericidad, ni coma ni astigmatismo, puede suceder que este punto imagen no est� en la posici�n correcta. Si el desplazamiento del punto es en la direcci�n paralela al eje �ptico, el resultaddo es que los puntos imagen est�n sobre una superficie curva, generalmente esf�rica, en lugar de una plana. Por eso a esta aberraci�n se le conoce con el nombre de curvatura de campo. En general, los oculares no pueden enfocar sobre superficie curva. En un telescopio con esta aberraci�n se puede enfocar claramente el centro del campo o la periferia, pero no ambos al mismo tiempo.

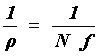(7)

donde N y f son el �ndice de refracci�n y la distancia focal de la lente, respectivamente. El astigmatismo y la curvatura de campo, como se puede ver, no son dos aberraciones independientes, por lo que el valor dado por esta expresi�n es v�lido s�lo en ausencia de astigmatismo.

Distorsi�n

Podr�a tambi�n suceder que el punto imagen se desviara de su posici�n ideal en una direcci�n perpendicular al eje �ptico. La imagen conserva entonces su definici�n y nitidez, pero cambia su forma, deformando la imagen. Con esta aberraci�n, llamada distorsi�n, la imagen de un cuadro es como se muestra en la figura 10, seg�n el signo de esta aberraci�n. En el caso de los telescopios astron�micos, esta aberraci�n es importante solamente si se desean hacer mediciones de las posiciones relativas de las im�genes estelares sobre el campo focal, a fin de determinar las posiciones de las estrellas. Por otro lado, en una lente simple o doblete, como es el caso de un telescopio refractor, la distorsi�n es sumamente peque�a.

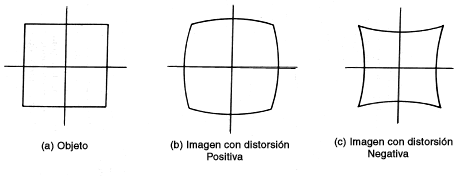
Figura 10. Im�genes de un objeto cuadrado cuando la lente tiene distorsi�n.

Aberraci�n crom�tica axial

Para complicar a�n m�s la situaci�n, el �ndice de refracci�n de los vidrios es diferente para cada color de la luz. La luz que emite o refleja un objeto es en general blanca, es decir, que est� formada por todos los colores posibles del arco iris o espectro. Entonces, puede suceder que las im�genes formadas por cada color est�n colocadas en diferentes planos o bien que tengan diferente tama�o. En el primer caso, se dice que el telescopio tiene aberraci�n crom�tica axial (Figura 11) y en el segundo aberraci�n crom�tica de amplificaci�n.

 

Figura 11. Aberraci�n crom�tica axial en una lente.

En un telescopio con aberraci�n crom�tica axial se puede enfocar solamente un color a la vez, por lo que la imagen de las estrellas tiene la forma de una mancha circular con n�cleo coloreado generalmente en rojo, rodeado de un halo de color azul (Figura 12[a]).

 

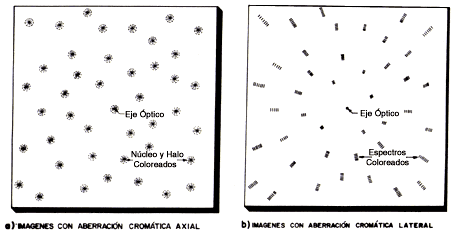
Figura 12. Im�genes estelares con aberraci�n crom�tica. (a) Axial. (b) De amplificaci�n.

Un telescopio reflector no tiene aberraci�n crom�tica, pues seg�n la ley de la reflexi�n, el �ngulo de reflexi�n es igual al de incidencia, cualquiera que sea el color de la luz. Sin embargo, en un telescopio refractor la aberraci�n crom�tica aparece si el objetivo es una lente convergente simple. Esta aberraci�n se puede corregir si el objetivo es un doblete formado por dos lentes en contacto, una convergente y una divergente, hechas de diferentes vidrios. Estas dos lentes deben tener aberraciones crom�ticas exactamente opuestas, a fin de que se anulen mutuamente, pero el poder refractor de la lente convergente debe ser superior al de la divergente para que el sistema sea convergente. Dicho de otro modo, la relaci�n entre el grado de refrangibilidad y el grado de dispersi�n crom�tica debe ser mayor en la lente convergente que en la divergente. Esto se logra si la lente divergente se construye con un tipo de vidrio �ptico com�nmente denominado Crown, y la lente divergente con un tipo de vidrio �ptico denominado Flint. Algunos de estos vidrios �pticos se enlistan en el cuadro 1. El llamado n�mero de Abbe V define el grado de dispersi�n crom�tica del vidrio, siendo tanto menor su magnitud cuanto mayor sea su dispersi�n crom�tica, y est� definido por

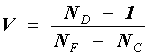(8)

donde las letras C, D y F, de acuerdo con una notaci�n propuesta por Fraunhofer, representan los colores rojo, amarillo y azul, respectivamente.

CUADRO 1. Caracter�sticas de algunos vidrios �pticos comunes.

Tipo de vidrio (cat�logo Schott)	NC l = 587.6 nm	ND l = 587.6 nm	NF l = 480.0 nm	V
Crown
Borosilicato	1.5143	1.5168	1.5224	64.20
BK-7
Crown
K-5	1.5198	1.5225	1.5286	59.64
Crown
Flint	1.6095	1.6127	1.6200	58.63
SK-4
Crown
Flint	1.5200	1.5231	1.5303	50.93
KF-5
Flint
F-2	1.61503	1.6200	1.6321	36.37
Flint
F-6	1.6311	1.6364	1.6491	35.35
Flint
Denso	1.6922	1.6989	1.7155	30.05

Un doblete acrom�tico se puede dise�ar con estos vidrios, usando las siguientes f�rmulas aproximadas, que nos permiten calcular las distancias focales de cada una de las dos componentes, como funci�n de la distancia focal F del doblete final y de los n�meros de Abbe de vidrios usados:

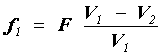(9)

 

 

y :

 

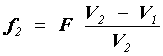(10)

 

Aberraci�n crom�tica lateral

Si no hay aberraci�n crom�tica axial sino solamente lateral o de amplificaci�n, las estrellas en el centro del campo son blancas, es decir, sin aberraci�n, pero a medida que se alejan del eje �ptico se alargan tomando la forma de peque�os espectros, o r�fagas de colores, seg�n se ve en la figura 12(b).

La aberraci�n crom�tica de amplificaci�n est� casi ausente en una lente simple, a pesar de su aberraci�n crom�tica axial, al igual que en un doblete acrom�tico. En cambio, esta aberraci�n puede ser muy notoria si el sistema �ptico est� formado por dos o m�s lentes separados, como es el caso de muchos oculares, o de un telescopio galileano. Aunque no siempre es posible, una manera de corregir esta aberraci�n en un sistema de dos lentes es haci�ndolas del mismo vidrio y separ�ndolas por una distancia igual a la semisuma de sus distancias focales.

Como se ir� viendo en el transcurso de este libro, mediante un dise�o adecuado es posible eliminar casi totalmente el efecto de estas aberraciones.

LA DIFRACCI�N DE LA LUZ EN UN TELESCOPIO

Es conveniente ahora recordar que el concepto de rayo de luz es solamente una idealizaci�n matem�tica que representa la realidad s�lo en forma aproximada. La luz es una onda de una naturaleza que llamamos electromagn�tica y que difiere de una onda de radio solamente en su longitud de onda. Cuando una onda, ya sea de luz, de radio o acusto-mec�nica como el sonido, pasa por una abertura, se produce un efecto llamado difracci�n. Al limitar la extensi�n lateral de la onda con la abertura el haz luminoso u onda cambia su direcci�n de propagaci�n cerca de los bordes, abriendo el haz un poco en forma de abanico. La desviaci�n angular del haz es tanto mayor cuanto menor sea la abertura del diafragma.

Como vimos antes, la pupila de un sistema �ptico limita la extensi�n lateral del haz luminoso; por lo tanto, es inevitable que se produzca el fen�meno de la difracci�n. Aunque seg�n la �ptica geom�trica o de rayos la imagen sea perfectamente puntual, debido a este fen�meno no ser� en realidad as�. La difracci�n har� que la imagen de una estrella supuestamente puntual sea en realidad un peque�o disco luminoso rodeado de unos anillos m�s d�biles, como se muestra en la figura 13(a). La irradiancia relativa a lo largo de un radio de esta imagen se muestra en la figura 13(b). Al primer anillo obscuro de esta imagen de difracci�n se le llama anillo de Airy, en honor de uno de los precursores en el estudio de este fen�meno.

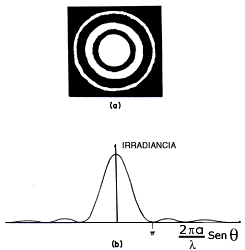
Figura 13. Imagen de una estrella. (a) Anillos de difracci�n. (b) Distribuci�n radial de la irradiancia en la imagen de difracci�n.

Las aberraciones se pueden corregir, pero la difracci�n no es posible eliminarla jam�s; s�lo se puede reducir su magnitud aumentando de tama�o la pupila, o sea, el di�metro de las lentes. Afortunadamente, el efecto de la difracci�n es en general muy peque�o comparado con el que casi siempre introduce aun peque�as aberraciones.

Debido a la difracci�n, en un telescopio perfecto, sin aberraciones, lo m�s juntas que pueden estar un par de im�genes de estrellas y aun distinguirlas como dos est� determinado por el llamado Criterio de Rayleigh. Este criterio, que se ilustra en la figura 14(b), nos dice que se tiene esta separaci�n m�nima cuando el centro de una imagen est� sobre el primer anillo oscuro o de Airy de la otra imagen. As�, la separaci�n angular q en radianes entre dos estrellas apenas detectables como separadas, est� dada por:

q = l.22 l / D

(11)

por lo que, substituyendo el valor de la longitud de onda (l= 5.55x l0^-5 cm) y convirtiendo q a segundos de arco, se encuentra:

q = 14/D

(12)

donde D est� expresado en cent�metros. Otra proposici�n de criterio de resoluci�n para dos estrellas muy cercanas fue propuesta por Sparrow, quien sugiri� que las estrellas pod�an estar un poco m�s juntas, de tal manera que la irradiancia de las dos estrellas, en la parte intermedia entre las dos, fuera aproximadamente constante, es decir, con una gr�fica plana, al pasar de una estrella a otra, como se ve en la figura 14(c). As�, seg�n el Criterio de Sparrow, la separaci�n angular m�nima en segundos de arco que podemos detectar entre dos estrellas est� dada por:

q = 11.6/D

(13)

donde D est� en cent�metros. El astr�nomo W. R. Dawes, despu�s de una cantidad muy grande de observaciones, encontr� emp�rica e independientemente un resultado muy similar al de Sparrow, por lo que este criterio se conoce tambi�n con el nombre de Criterio de Dawes. Es importante hacer notar que estos criterios son rigurosamente v�lidos s�lo para observaci�n visual, con la condici�n adicional de que las dos estrellas tengan la misma magnitud.

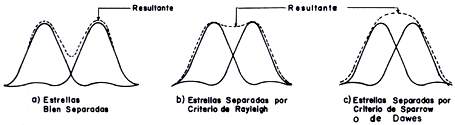
Figura 14. Criterios de Rayleigh, de Sparrow y de Dawes para la resoluci�n de dos estrellas muy cercanas.

LA TURBULENCIA ATMOSF�RICA

La atm�sfera est� en continuo movimiento y agitaci�n debido a las diferencias locales de temperatura. Como las variaciones en temperatura ocasionan tambi�n variaciones en el �ndice de refracci�n, la imagen de una estrella se desenfocar� y mover� continuamente.

El primero que se dio cuenta de la importancia de la turbulencia atmosf�rica o seeing (del ingl�s: visi�n), como le llaman los astr�nomos, fue Christian Huygens en Holanda quien not� que las estrellas cintilaban y que las orillas de la Luna y de los planetas vibraban aun cuando la atm�sfera estaba aparentemente calmada y serena.

Una consecuencia importante del seeing atmosf�rico es que aumenta el tama�o de las im�genes de las estrellas y adem�s las desplaza constantemente de su posici�n, y con ello disminuye el poder resolutor del telescopio. Podemos imaginarnos la turbulencia atmosf�rica como celdas o globos de aire en continuo movimiento, con variaciones de una a otra en el �ndice de refracci�n. Cada celda tiene un di�metro entre 10 y 25 cent�metros. Por lo tanto, en telescopios con aberturas menores de 10 cent�metros el efecto de la turbulencia es un movimiento continuo y al azar, con desenfoques ocasionales de la imagen. Esta es la raz�n de la cintilaci�n de las estrellas cuando se ven a simple vista. Si la abertura del telescopio es mucho mayor de 20 cent�metros, la imagen no se mueve, sino que su tama�o aumenta, y adquiere una forma que en promedio es circular, pero que cambia constantemente. El di�metro aparente de las estrellas debido a este efecto depende del lugar, el d�a y la hora, y puede variar desde unos cuantos segundos de arco hasta dos o tres d�cimos de segundo de arco en las monta�as de los mejores observatorios astron�micos del mundo. Por ejemplo, en el observatorio de Monte Palomar, el di�metro m�s frecuente de la imagen es de alrededor de dos y medio segundos de arco, con valores mayores o menores en ocasiones. El valor m�s peque�o que se ha observado ah� es de alrededor de tres d�cimas de segundo de arco.

Tanto la turbulencia atmosf�rica como otro efecto adicional que es la aberraci�n crom�tica de la atm�sfera, aumentan r�pidamente con la altura de observaci�n, por lo que las observaciones deben efectuarse lo m�s cerca del zenit, de ser posible.

FACTORES LIMITANTES DE LA RESOLUCI�N DE UN TELESCOPIO

En telescopios pobremente dise�ados los factores limitantes son las aberraciones. Esto no tiene por qu� suceder en los telescopios modernos, dise�ados y construidos por profesionales. Sin embargo, esto era muy com�n en los telescopios antiguos. Un ejemplo sumamente interesante es el telescopio de Galileo, que ten�a todo tipo de aberraciones, incluyendo la de esfericidad y la crom�tica axial, que son las m�s necesarias de corregir. Este telescopio ten�a una resoluci�n angular de tan s�lo 15 segundos de arco.

En los telescopios modernos los factores importantes que limitan la resoluci�n angular son la difracci�n, si la abertura es menor de alrededor de 25 cm, y la turbulencia atmosf�rica si su abertura es mayor. Dicho de otro modo, la mayor resoluci�n que puede tener un telescopio terrestre es la que le permita la atm�sfera, y se logra con una abertura de tan s�lo 25 cm, como se ve en el cuadro 4. Un telescopio en �rbita, fuera de la atm�sfera terrestre, podr� tener una resoluci�n mayor.

AMPLIFICACI�N �TIL DE UN TELESCOPIO

La amplificaci�n de un telescopio est� dada por el cociente de las distancias focales del objetivo y del ocular. Por lo tanto, en teor�a es posible, mediante el ocular adecuado, obtener cualquier amplificaci�n que se desee. En la pr�ctica esto no es posible porque pasado un cierto l�mite, el tama�o de un elemenfo de imagen o "grano" puede ser tan grande que ya no aumenta la cantidad de detalle que se puede ver al aumentar la amplificaci�n. A �sta se le llama algunas veces "amplificaci�n vac�a". Este l�mite se alcanza cuando el elemento de imagen tiene justamente el di�metro angular que puede resolver el ojo humano.

Este l�mite de resoluci�n del ojo humano es de alrededor de un minuto de arco, pero al observar a trav�s de un telescopio con alta amplificaci�n, la pupila de salida frecuentemente es menor que la del ojo, por lo que una resoluci�n de dos minutos de arco, es decir, de 120 segundos de arco, es m�s realista. El límite de resoluci�n de Dawes nos dice que la resoluci�n angular del telescopio en el campo del objeto es de 1l.6/D segundos de arco, pero este elemento de imagen visto a trav�s del telescopio con amplificaci�n M tiene un di�metro angular igual a 11.6 M/D segundos de arco. Si ahora hacemos que este di�metro angular sea igual a 120 segundos de arco, encontramos f�cilmente que la m�xima amplificaci�n �til para telescopios peque�os limitados por difracci�n se alcanza aproximadamente cuando

M = l0 D

(14)

es decir, cuando la amplificaci�n es aproximadamente igual a 10 veces el di�metro de la abertura del telescopio expresada en cent�metros, o lo que es lo mismo, el di�metro de la abertura en mil�metros. (V�ase cuadro 4.) Debido a la turbulencia atmosf�rica, esta amplificaci�n m�xima del telescopio jam�s podr� ser mucho mayor de poco m�s de 250 a 500 ni siquiera en telescopios tan grandes como el de Monte Palomar.

MAGNITUD LIMITE DE UN TELESCOPIO

La magnitud de una estrella es una indicaci�n de su brillantez, de tal manera que cuanto m�s brillante sea, menor ser� su magnitud. Seg�n una escala arbitraria y subjetiva de los griegos, las estrellas m�s brillantes tendr�n magnitud uno, mientras que las m�s d�biles que se pueden observar a simple vista tendr�n magnitud seis. Esta manera de medir la brillantez de las estrellas se ha conservado hasta nuestros d�as, pero con un sentido f�sico y matem�tico m�s formal. Ahora se sabe que en la respuesta del ojo, seg�n una ley psicof�sica de Fechner, la sensaci�n es proporcional al logaritmo de la excitaci�n. John Herschel, en 1830, defini� las magnitudes estableciendo que la brillantez de una estrella de primera magnitud es 100 veces mayor que la de una estrella de sexta magnitud. De acuerdo con esto, una estrella con una magnitud una unidad menor que otra, tendr� una brillante veces mayor. Por lo tanto, si suponemos que el brillo de una estrella de primera magnitud es uno, se tienen las siguientes equivalencias:

CUADRO 2. Equivalencia entre magnitud y brillo relativo de las estrellas.

Magnitud	Brillo relativo
-1	6.3
0	2.5
1	1
2	1/2.5
3	1/6.3
4	1/15.8
5	1/39.8
6	1/100
7	1/251.2
8	1/630.9

Si dos estrellas con magnitudes m y n tienen brillos B_n y B_m, respectivamente, se tiene que

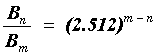
(15)

de donde, tomando logaritmos, se obtiene

log Bn - log Bm = (m - n) log (2.512) = 0.4 (m - n)

(16)

o sea que la diferencia de las magnitudes es directamente proporcional a la diferencia de los logaritmos de sus brillos.

Falta ahora calibrar esta escala seleccionando el brillo de una estrella de primera magnitud; esto se hizo de tal manera que las estrellas Aldebar�n y Altair est�n muy cercanas a ella. El siguiente cuadro lista como ejemplos las magnitudes visuales de algunas estrellas.

CUADRO 3. Magnitudes visuales de algunas estrellas.

Estrella	Nombre	Magnitud
alfa can Mayor	Sirio	- 1.5
alfa corina	Canopus	- 0.1
alfa Lira	Vega	0.0
alfa Orión	Betelgueuse	0.5
alfa Águila	Altair	0.8
alfa Tauro	Aldebarán	0.9
alfa Osa Mayor	Doubne	1.8
alfa Osa Menor	Polar	2.0
beta Lira		3.5
delta Lira		4.0
nu Lira		5.0
épsilon Lira		6.0

Si se observa una estrella a trav�s de un telescopio, el brillo aparente de la estrella aumenta debido a que la abertura colectora del objetivo del telescopio es mayor que la del ojo. Por lo tanto, para poder alcanzar a percibir una estrella a trav�s del telescopio, no es necesario que sea tan brillante como cuando se le observa a simple vista. Dicho de otro modo, el brillo m�nimo necesario para ver una estrella es inversamente proporcional al cuadrado del di�metro del telescopio con el que se le observa. Entonces, la relaci�n entre el brillo m�nimo para poder observar una estrella a trav�s del telescopio y el brillo m�nimo para poder observarla a simple vista es el cuadrado de la relaci�n del di�metro Do de la pupila del ojo entre el di�metro D_t de la abertura del telescopio. Por lo tanto

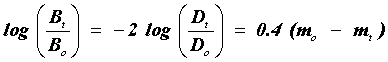
(17)

donde m₀ y m_t son las magnitudes m�s d�biles que se pueden observar a simple vista y a trav�s del telescopio. De aqu� obtenemos

mt - m0 + 5 log

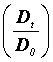(18)

donde el sub�ndice t se refiere al telescopio y el sub�ndice o al ojo. El di�metro de la pupila del ojo es diferente para diferentes observadores, pero podemos suponer un promedio de alrededor de 0.6 cm. Si tomamos este di�metro de Do y la magnitud límite m_o que se observa a simple vista, igual a 6, se obtiene:

Mv = 7.10 + 5 log D

(19)

Aqu� se ha suprimido el sub�ndice del di�metro del telescopio por no ser ya necesario, y se ha cambiado el sub�ndice de la magnitud a v para indicar que la observaci�n a trav�s del telescopio es visual. Este resultado se tabula en el cuadro 4. De aqu� se ve que con el telescopio de Yerkes de un metro de di�metro se puede observar hasta la magnitud 17, y con un telescopio de 10 cm de abertura, hasta la magnitud 12.

Otra manera de ver las ventajas de un telescopio con abertura grande es imaginarnos que las estrellas y galaxias tienen brillos absolutos muy diferentes, pero distribuidos completamente al azar en todo el espacio. As�, una estrella dada la podr�amos detectar a una mayor distancia con un telescopio de abertura grande que con otro de menor abertura. Los brillos aparentes var�an en relaci�n inversa con el cuadrado de la distancia y en relaci�n directa con el cuadrado de la abertura del telescopio. Por lo tanto, un telescopio con el doble de abertura de otro puede detectar objetos al doble de distancia. Es entonces obvio que con un telescopio del doble de la abertura de otro se pueden observar objetos celestes al doble de la distancia, y por lo tanto un volumen m�s grande del universo que nos rodea.

Fotogr�ficamente, la magnitud l�mite depende no s�lo del di�metro del objetivo sino tambi�n de la sensibilidad de la pel�cula y del tiempo de exposici�n, como se explicar� m�s adelante en la secci�n sobre telescopios fotogr�ficos.

CUADRO 4. Principales caracter�sticas de un telescopio, seg�n el di�metro de su objetivo.

Diámetro del objetivo en cm.	Poder resolutor en segundos de arco		Amplificación visual máxima útil	Magnitud visual límite
	Rayleigh	Sparrow
0.60	23.33	19.33	6	6.0
5.00	2.80	2.32	50	10.6
10.00	1.40	1.16	100	12.1
15.00	.93	.77	150	12.9
20.0	.70	.58	200	13.6
25.0	.56	.46	250	14.0
30.0	.46	.38	300	14.4
50.00	.28	.23	500	15.6
60.00	.23	.19	600	16.0
80.00	.17	.14	800	16.6
100.00	.14	.11	1 000	17.1
150.00	.09	.07	1 500	18.0
200.00	.07	.05	2 000	18.6
250.00	.05	.04	2 500	19.0
300.00	.04	.03	3 000	19.4
500.00	.02	.02	5 000	20.5

NOTA: Los valores muy por debajo de la línea divisoria punteada no tienen validez en la superficie terrestre, debido a la turbulencia atmosférica.

BRILLANTEZ DE LA IMAGEN DE UN TELESCOPIO

Es f�cil ver que un telescopio kepleriano el m�ximo flujo de la energ�a luminosa al ojo se obtiene cuando el di�metro del objetivo es igual que el di�metro de la pupila del ojo, multiplicado por la amplificaci�n, es decir, cuando la pupila de salida es del mismo di�metro que la pupila del ojo, a fin de aprovechar al m�ximo la capacidad de captaci�n de luz del ojo del observador.

Si crece el di�metro del objetivo, crece la pupila de salida, y con ello la cantidad de luz colectada. Pero en un telescopio visual esta energ�a luminosa no se puede aprovechar, pues la pupila de salida se hace mayor que la del ojo. Dicho de otro modo, dado un di�metro del objetivo, se puede aumentar la luminosidad del objeto disminuyendo la amplificaci�n, y por lo tanto aumentando el di�metro de la pupila de salida, hasta el l�mite de igualarla con el di�metro de la pupila del ojo. Esta amplificaci�n, para la cual se obtiene la m�xima brillantez del objeto, est� dada por:

Mmin = = D/0.6

(20)

que es el m�nimo valor que puede tener la amplificaci�n sin desperdiciar parte de la energ�a captada por el telescopio. D es el di�metro del objetivo en cent�metros. As�, un telescopio de 12 cent�metros de di�metro tendr� la m�xima brillantez visual de la imagen si su amplificaci�n es de 20.

La brillantez de la imagen de un objeto puntual, como una estrella, es directamente proporcional al cuadrado del di�metro de la pupila de entrada, suponiendo que no excede el di�metro m�ximo antes explicado, y es independiente de la amplificaci�n de telescopio, pues la imagen es siempre un punto. Como ya vimos, la relaci�n entre la brillantez de la imagen a trav�s del telescopio y la brillantez de la imagen a simple vista est� dada por el cuadrado de la relaci�n del di�metro de la pupila de entrada del telescopio y el di�metro de la pupila del ojo, seg�n la expresi�n:

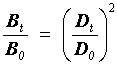(21)

Por otro lado, de igual manera, la brillantez de la imagen de un objeto extendido es directamente proporcional al cuadrado del di�metro de la pupila de entrada, pero tambi�n es inversamente proporcional al cuadrado de la amplificaci�n. La raz�n es que al aumentar la amplificaci�n aumenta el di�metro de la imagen, y con ello el �rea sobre la cual distribuye la energ�a luminosa captada por el telescopio. Es f�cil demostrar que la relaci�n entre la brillantez de la imagen a trav�s del telescopio y la brillantez de la imagen a simple vista est� dada por el cuadrado de la relaci�n del di�metro de la pupila de entrada del telescopio y el di�metro de la pupila del ojo, dividido entre la amplificaci�n del telescopio, como sigue:

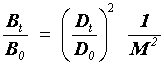(22)

Si ahora suponemos que la amplificaci�n es igual a la amplificaci�n M_min que produce la m�xima brillantez (M = M_min), encontramos que la brillantez a trav�s del telescopio es la misma que cuando se observa el objeto a simple vista. El resultado es sumamente importante y de gran utilidad, pues nos dice que la brillantez de un objeto extendido no podr� jam�s aumentar por el uso de un telescopio, sino que en el mejor de los casos ser� la misma.

Es por lo tanto f�cil ver que la relaci�n entre la brillantez de la imagen de un objeto puntual y la brillantez de la imagen de un objeto extendido es directamente proporcional a la amplificaci�n del telescopio, como sigue:

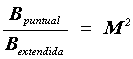(23)

siempre y cuando esta amplificaci�n sea mayor que M_min. Por lo tanto, esta relaci�n siempre es mucho mayor que uno. �sta es la raz�n por la cual es posible observar las estrellas m�s brillantes a trav�s de un telescopio, a plena luz del d�a, cuando es completamente imposible hacerlo a simple vista.

RESUMEN DE LAS CARACTER�STICAS DE UN TELESCOPIO

Las caracter�sticas principales que describen el funcionamiento de un telescopio se resumen a continuaci�n en el siguiente cuadro:

CUADRO 5. Caracter�sticas de funcionamiento de un telescopio

Diámetro del objetivo en cm	mínima	Amplificación óptima	máxima	Magnitud límite	resolución límite
2	3	5	20	8.6	5.8
5	8	12	50	10.6	2.32
10	16	25	100	12.1	1.16
15	25	37	150	13.0	.77
20	33	50	200	13.6	.58
25	42	62	250	14.1	.46
30	50	75	300	14.5	.39
40	66	100	400	15.1	.29
50	83	125	500	15.6	.23
60	100	150	600	16.0	.19

Se ha definido aqu� amplificaci�n m�nima como aquella que nos produce una pupila de salida de 6 mm y por lo tanto produce la m�xima luminosidad posible. Esta amplificaci�n es ideal si se desea ver el cielo con la m�xima luminosidad que permite el telescopio.

Como es de esperar, dado un di�metro del objetivo, la m�nima amplificaci�n es la que tiene el m�ximo campo visual. Por otro lado, como se puede ver en el cuadro 5, cuanta m�s abertura tenga el telescopio mayor ser� la amplificaci�n m�nima, reduciendo el campo visual, pero tambi�n aumentando la magnitud l�mite. Si el cielo tuviera una densidad volum�trica uniforme de estrellas, la reducci�n en el campo visual quedar�a justamente compensada por el aumento en la magnitud l�mite. Por lo tanto, cualquiera que fuera el di�metro del objetivo, la amplificaci�n m�nima siempre producir� la misma densidad de estrellas en el campo visual. Se ha encontrado, sin embargo, que �ste no es el caso, y que el di�metro �ptimo de la abertura para tener la mayor densidad de estrellas en el campo es alrededor de 15 cent�metros. Este tipo de telescopio recibe el nombre de telescopio del campo estelar m�s rico.

La amplificaci�n �ptima se ha definido aqu� como aquella que da la mejor resoluci�n visual aparente, la cual se obtiene cuando la pupila de salida tiene un di�metro de 0.4 cent�metros. Para observaci�n planetaria, sin embargo, se recomienda aproximadamente el triple de esta amplificaci�n, siempre que no exceda a la amplificaci�n m�xima.

La amplificaci�n m�xima es aquella que se puede obtener con un telescopio sin aberraciones, llev�ndolo al l�mite que nos permite la difracci�n, aunque hay que recordar que dependiendo del grado de turbulencia atmosf�rica, este límite puede estar cuando mucho en un valor aproximado de 250 a 500.

La magnitud l�mite es para observaci�n visual y de ninguna manera se aplica a telescopios fotogr�ficos.

La resoluci�n angular se expresa en segundos de arco, seg�n el criterio de Dawes.