LA SUPERCONDUCTIVIDAD EN IM�GENES

Figura I. El efecto Meissner. En esta figura se muestra la "levitaci�n" de un im�n por la presencia de un superconductor. Esto ocurre debido al efecto Meissner. El im�n, que en la fotograf�a tiene la forma de una moneda, se encuentra suspendido por fuerzas magn�ticas. La pastilla cer�mica se encuentra en la parte inferior y esta inmersa en nitr�geno l�quido para mantenerla a una temperatura por debajo de su temperatura de transici�n y para que pueda as� encontrarse en el estado superconductor. El efecto Meissner consiste en lo siguiente: al acercar un im�n a un material superconductor se genera, magn�ticamente, una imagen de �l como si el superconductor fuera un espejo. De esta manera, el im�n es siempre repelido por su imagen o lo que es lo mismo, por el superconductor. La fuerza de repulsi�n es capaz de contrarrestar el peso del im�n, produciendo la levitaci�n. Una aplicaci�n de este efecto se da en veh�culos de transporte masivo que "flotan" sin fricci�n con el piso y que reciben el nombre de magneplanos, porque virtualmente se desplazan volando. La pastilla cer�mica es del compuesto 1-2-3 de itrio, Bario y cobre con una temperatura de transici�n de 89 Kelvin . La pastilla se prepar� en el Instituto de F�sica de la UNAM en donde se tom� tambi�n la fotograf�a.

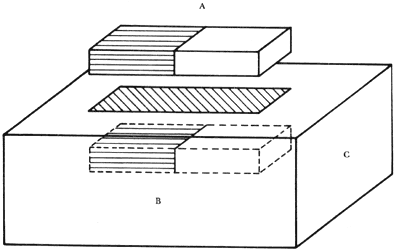
Figura II. Aqu� se presenta un esquema de c�mo se produce el efecto Meissner. Al acercar un im�n (A) a un superconductor (B), se produce en este una imagen magn�tica (C) que lo repele. La intensidad de la fuerza de repulsi�n determina la altura a la que puede "flotar" el im�n. Conforme m�s poderoso sea el im�n, más poderosa ser� su imagen y mas intensa ser� la fuerza de repulsi�n, produciendo una flotaci�n a mayor altura. Todo esto ocurre sin importar si el im�n est� quieto, traslad�ndose o girando sobre s� mismo. Siempre aparece una imagen instant�nea de el en el superconductor, que lo repele y lo hace flotar. Por el efecto Meissner sabemos que el estado superconductor es un estado de la materia en el que no existe resistencia al paso de la corriente el�ctrica y en el que los electrones se hallan en un estado muy especial de gran poder y correlaci�n de unos con otros. En virtud de este estado, los campos magn�ticos no pueden penetrar al superconductor. La manera en que el superconductor genera la imagen del im�n es moviendo a los electrones, generando corrientes superficiales que, a su vez, generan un campo magn�tico que corresponden exactamente a la imagen del im�n , produci�ndose as� la repulsi�n y, por lo tanto, la levitaci�n.

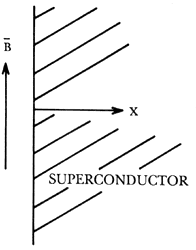
Figura III. Un superconductor en presencia de un im�n. El im�n queda representado por un campo de fuerzas magn�ticas simbolizadas por B. Cabe se�alar que un campo magn�tico puede ser generado no solamente por materiales ferromagn�ticos, sino tambi�n por cualquier corriente el�ctrica. Esto es, cualquier corriente el�ctrica es equivalente a un im�n y capaz de desviar a una br�jula colocada en su vecindad. La respuesta del superconductor ante la presencia del campo magn�tico se ilustra en la figura IV.

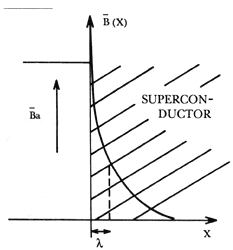
Figura IV. Cuando el campo magn�tico B intenta penetrar al superconductor, �ste genera corrientes el�ctricas superficiales que producen un campo magn�tico que se opone a B, cancel�ndolo en el interior del superconductor despu�s de una distancia de la superficie del material que es, t�picamente, del orden de un angstrom. Este fen�meno, que es el efecto Meissner, constituye una de las caracter�sticas esenciales de un superconductor. Sin el efecto Meissner, no podemos decir que tenemos un superconductor. Hay que hacer notar que cuando un material no tiene resistencia el�ctrica recibe el nombre de conductor perfecto. As�, todo superconductor es un conductor perfecto, ya que tiene resistencia el�ctrica cero. Pero el ser un conductor perfecto no es suficiente para ser un superconductor. Es necesario agregar el efecto Meissner. En otras palabras, aunque un superconductor es un conductor perfecto, no todo conductor perfecto es un superconductor. La diferencia estriba en el efecto Meissner. Puede demostrarse que las propiedades magn�ticas de un conductor perfecto no llevan al efecto Meissner, son propiedades distintas de las de un superconductor. En esencia, en un conductor perfecto el campo magn�tico siempre debe ser constante y en el superconductor siempre debe ser cero, que es un requerimiento mucho m�s fuerte.

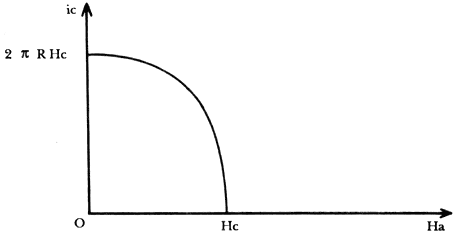
Figura V. Las corrientes cr�ticas para un superconductor Tipo I. La corriente crítica se define como aquella para la cual se destruye el estado superconductor. En virtud de que cuando un alambre porta una corriente el�ctrica se genera a su alrededor un campo magn�tico, las corrientes criticas y los campos cr�ticos est�n �ntimamente relacionados. Por eso esperamos que exista un valor m�ximo de la corriente que un superconductor puede llevar y que esta corriente m�xima dependa del campo magn�tico aplicado a la muestra. En ausencia de campo magn�tico, las corrientes cr�ticas de los superconductores pueden ser muy altas. Por ejemplo, para el caso de plomo, si tenemos un alambre de 1 mm de di�metro, enfriado a la temperatura de ebullici�n del helio l�quido (4.2 K) el alambre puede llevar hasta 140 amperios de corriente superconductora, esto es, sin resistencia el�ctrica. En un campo magn�tico la corriente cr�tica es menor. La figura muestra la forma en que la corriente cr�tica se reduce por la presencia de un campo magn�tico aplicado externamente. Aqu�, el campo magn�tico est� en direcci�n paralela al eje del cilindro, de manera que el factor de desmagnetizaci�n por la forma es cero. La expresi�n algebraica de esta variaci�n est� dada por:

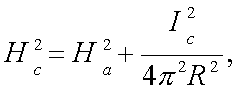
donde H_C es el campo cr�tico para una temperatura dada, H_a es el campo aplicado, I_C es la corriente cr�tica y R es el radio del alambre.

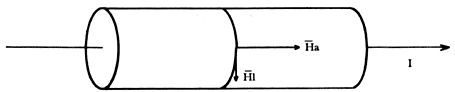
Figura VI. Alambre superconductor cil�ndrico Tipo I que lleva una corriente I, con un campo magn�tico, H_a, aplicado a lo largo del alambre. Al pasar una corriente por el alambre se genera un campo magn�tico perpendicular a �l, H_I. El campo magn�tico resultante es la suma vectorial de estos dos. En este caso el factor de desmagnetizaci�n por la forma es cero. Los dos vectores est�n formando un �ngulo recto, de manera que la magnitud del campo resultante se halla por el teorema de Pit�goras y lleva a la relaci�n entre el campo cr�tico, campo aplicado y corriente cr�tica dada en la figura V y que corresponde al arco de una elipse.

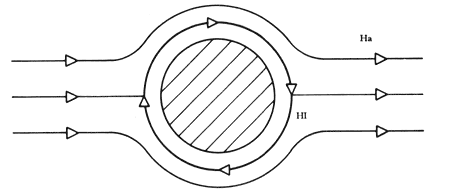
Figura VII. Muestra cil�ndrica superconductora Tipo I en el seno de un campo magn�tico perpendicular al eje del cilindro. En este caso, el factor de desmagnetizaci�n es �. La corriente fluye en una direcci�n perpendicular al plano de la p�gina. De este modo, el campo aplicado, H_a, y el campo generado por la corriente que circula por el alambre se suman en la parte superior de la secci�n transversal del alambre y se restan en la parte inferior. Si suponemos campos suficientemente d�biles, que no lleven a la muestra al estado intermedio, la corriente cr�tica para este caso est� dado por:

donde la notaci�n es la misma que en la figura V.

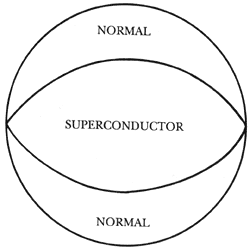
Figura VIII. El estado intermedio es una consecuencia de la forma geom�trica del superconductor. Es sabido en electromagnetismo que el campo resultante en el interior de un cuerpo puede ser mayor que el campo aplicado externamente debido al factor de desmagnetizaci�n por la forma (v�ase el cap�tulo II, "El estado intermedio"). Como consecuencia, existen en la periferia de la muestra, regiones sometidas al campo cr�tico aun antes de que el campo externo llegue al valor del campo cr�tico para la sustancia correspondiente. A primera vista uno pudiera esperar que toda la muestra pasara al estado normal tan pronto se llegara al campo cr�tico en su periferia, pero caer�amos en el absurdo de que toda la muestra pasara al estado normal con un campo aplicado inferior al campo cr�tico de la sustancia. Como consecuencia, tendr�amos un cuerpo con regiones en el estado normal cerca de su periferia y en estado superconductor cerca de su centro, tal como se muestra. Est� configuraci�n resulta imposible de sostener, en virtud de que se puede aplicar el mismo razonamiento a la porci�n de material que queda en el estado superconductor, hasta transformar toda la muestra al estado normal. La soluci�n a este problema se halla d�ndose cuenta de que las fases normales superconductoras pueden coexistir una junto a la otra del mismo modo que coexiste un liquido con su vapor. De esta manera se puede tener, alternadamente, regiones en el estado superconductor y regiones en el estado normal, lleg�ndose de este modo a una configuraci�n de equilibrio.

Figura IX. Evidencia experimental del estado intermedio. Uno de los m�todos para la observaci�n del estado intermedio se basa, como en este caso, en la tendencia de las part�culas de material ferromagn�tico (limaduras de hierro, por ejemplo) a acumularse en regiones de alta densidad de campo magn�tico, y de part�culas de material superconductor (que es un diamagneto perfecto, ya que no permite el paso de ning�n campo magn�tico a su interior) a acumularse en regiones de baja intensidad de campo magn�tico. La fotograf�a, tomada de un trabajo realizado en 1957 y publicado por B. M. Baloshova e I. W. Sharvin en el vol. 4, p. 54 de la revista Soviet Physics. JETP, tambi�n de 1957, muestra una esfera de plomo de 3 cm de di�metro por debajo de su temperatura de transici�n superconductora, cubierta de un polvo de niobio (que se vuelve superconductor a una temperatura mayor que la temperatura de transici�n del plomo y es un diamagneto perfecto en la fotograf�a). La alternancia de las zonas claras y oscuras muestra la alternancia de zonas en estado normal con zonas en el estado superconductor. El factor de desmagnetizaci�n por la forma para la esfera es de 1/3 y se encuentra en el estado intermedio. Las zonas oscuras son superconductoras.

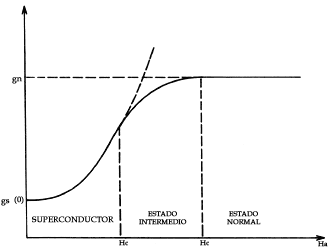
Figura X. Valores de la energ�a libre de un superconductor sometido a un campo magn�tico externo y con un factor de desmagnetizaci�n distinto de cero. La l�nea continua muestra la evoluci�n de la energ�a libre del material conforme aumenta la intensidad del campo magn�tico aplicado externamente. Se puede ver claramente que para el estado intermedio la energ�a del material es menor que si permaneciera totalmente en el estado superconductor y que tambi�n es menor que la energ�a que tendr�a el material si pasara todo al estado normal. En la naturaleza todas las cosas tienden a un estado de energ�a m�nima. As�, el superconductor con un factor de desmagnetizaci�n por la forma distinto de cero "prefiere" encontrarse en el estado intermedio para valores del campo aplicado comprendidos entre H'_C y H_C, que ser totalmente superconductor o totalmente normal.

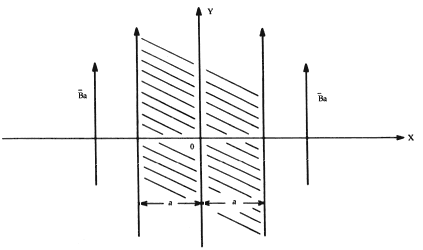
Figura XI. Pel�cula delgada superconductora en el seno de un campo magn�tico. Ya hemos visto que un campo magn�tico externo penetra unos cuantos angstroms en el interior de un superconductor. Este hecho tiene consecuencias relevantes en el caso de las pel�culas delgadas. El campo magn�tico cr�tico para un material aumenta si �ste se presenta en forma de pel�cula delgada. La magnitud del aumento depende de las dimensiones de la muestra con respecto a la profundidad de penetraci�n del campo a partir de la superficie. El efecto es notable solamente si el volumen contenido dentro de la profundidad de penetraci�n del campo magn�tico es comparable con el volumen total de la muestra. Se puede demostrar que para temperaturas no muy cercanas a la temperatura de transici�n (desde luego, por debajo de �sta) el aumento del campo cr�tico ser� mayor de 10% si el espesor de la pel�cula es inferior a 5 000 angstroms. Para el caso de una pel�cula muy delgada, digamos de 100 angstroms o menos, el campo cr�tico puede crecer por un factor de 10, especialmente si la temperatura de la muestra es cercana a la temperatura cr�tica del material. De aqu� la importancia tecnol�gica de obtener pel�culas delgadas superconductoras, especialmente con los nuevos materiales cer�micos superconductores de alta temperatura cr�tica.

Figura XII. Secci�n transversal t�pica de una pel�cula delgada obtenida por evaporaci�n. N�tese la disminuci�n gradual del espesor en los bordes. Una consecuencia importante de la dependencia del valor del campo cr�tico en el espesor de la pel�cula del material es que la definici�n de la transici�n magn�tica de una pel�cula delgada depende mucho de la naturaleza de sus bordes. Por regla general, los bordes de las pel�culas preparadas son como se muestra. Al ser los bordes m�s delgados que el resto de la pel�cula, tienen un campo cr�tico mayor. Si la prueba para verificar que la pel�cula delgada es superconductor consiste en pasar una corriente a trav�s de ella y ver si aparece una diferencia de potencial en sus bordes, �stos permanecer�n en el estado superconductor y dar�n lugar a una resistencia cero aun si el resto de la pel�cula ya se encuentra en estado normal. Esto tiene dos consecuencias inmediatas: primero, la intensidad de campo magn�tico al cual aparece un voltaje (esto es, transici�n al estado normal) puede ser considerablemente mayor que el verdadero campo cr�tico de la pel�cula; segundo, como es muy poco probable que los bordes sean perfectamente uniformes a lo largo de la pel�cula, la transici�n del estado de resistencia cero al estado normal puede ser muy ancha con respecto al campo magn�tico aplicado externamente. Para obtener una transici�n mucho mejor definida, lo que generalmente se hace es recortar los bordes para tener los extremos del mismo grosor que el resto de la pel�cula.

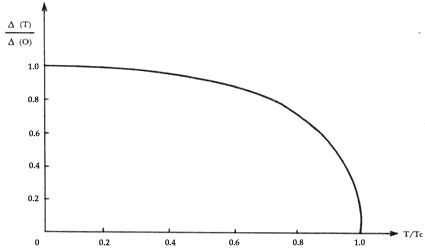
Figura XIII. Variaci�n de la banda de energ�a prohibida a los electrones superconductores con respecto a la temperatura. Una de las caracter�sticas m�s importantes de un superconductor es la presencia de una banda de energ�a prohibida a los electrones, situaci�n semejante a la que se tiene en un semiconductor. La presencia de esta banda hace que los electrones superconductores requieran, al menos, la energ�a que corresponde a la anchura de esta banda para pasar al estado normal. Conforme crece la temperatura, disminuye la energ�a para hacer que un electr�n pase al estado normal, esto es, para que se rompa un par de Cooper. Cualquier teor�a que explique la superconductividad tendr� que predecir la variaci�n de esta banda correctamente. La figura muestra la predicci�n que se realiza, por la teor�a de BCS (teor�a de Bardeen, Cooper y Schrieffer, formulada en 1957). Los resultados experimentales para los superconductores convencionales (no para los nuevos superconductores cer�micos de alta temperatura cr�tica) se apegan muy bien a las predicciones de la teor�a BCS. Para los nuevos materiales cer�micos a�n hay mucha controversia sobre la manera en que esta banda cambia con la temperatura, mas hay indicaciones de que la variaci�n de esta banda con la temperatura se parece mucho a la predicci�n que se hace con la teor�a BCS, pero todav�a se requieren m�s verificaciones.

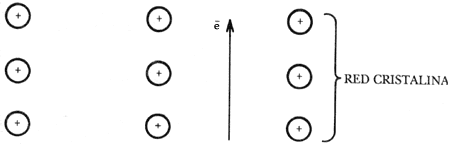
Figura XIV. Esquema de un electr�n viajando a trav�s de la red cristalina. En los materiales superconductores convencionales, la red cristalina de iones desempe�a un papel important�simo en la aparici�n de la superconductividad. Puede demostrarse que cuando existe una fuerza efectiva de atracci�n entre dos electrones, pertenecientes a un metal, estos electrones quedan ligados entre s�, sin importar la intensidad de la fuerza. A la pareja de electrones ligados entre s� se les conoce como par de Cooper. Actualmente es muy claro que para los superconductores convencionales el origen de la fuerza de atracci�n es la interacci�n electr�n-electr�n mediada por la red cristalina. A esta interacci�n se le conoce com�nmente como de electr�n-fon�n-electr�n. Para los nuevos superconductores cer�micos se tiene ya muy claro que existen los pares de Cooper. Sin embargo, a�n no es claro el mecanismo o mecanismos que llevan a su formaci�n. Hay evidencias de que la red cristalina interviene en la formaci�n de los pares de Cooper, pero no como el �nico mecanismo.

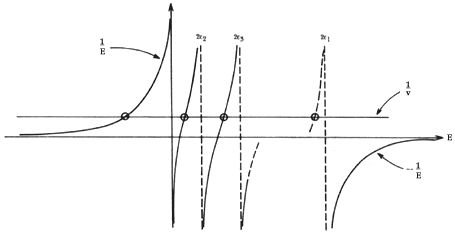
Figura XV. Esquema de la soluci�n num�rica de las ecuaciones que resultan para la energ�a de un par de Cooper. El valor de la energ�a de los dos electrones en el metal que interaccionan atractivamente queda dada por la intersecci�n de la recta se�alada como I/V y las curvas verticales en la figura. Puede verse que existen muchas respuestas posibles para el valor de la energ�a, sin embargo, solamente existe una soluci�n de valor negativo para la energ�a que implica que los electrones quedan ligados el uno al otro. La letra V representa a la intensidad de la fuerza de atracci�n. N�tese que sin importar que tan d�bil sea la atracci�n entre los electrones del par, siempre existir� una intersecci�n del lado de energ�as negativas. Esto significa que siempre se podr� obtener una pareja de electrones ligados entre s� cuando exista una interacci�n efectiva de atracci�n entre ellos, sin importar que tan d�bil sea esta.

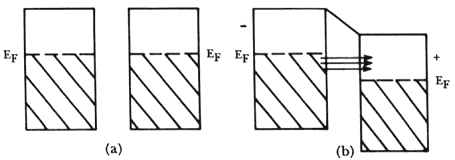
Figura XVI. Diagrama de niveles de energ�a de dos metales normales a trav�s de los cuales se da el llamado efecto t�nel de los electrones para pasar de un metal a otro. La zona representa estados electr�nicos ya ocupados por los electrones en cada metal. La parte blanca muestra los estados disponibles. A temperatura cero, el paso de los electrones de un metal a otro queda completamente prohibido por el principio de exclusi�n de Pauli. Cuando se aplica un voltaje positivo al metal de la derecha, de manera tal que los niveles de energ�a de Fermi, E_F, ya no coinciden, hay estados ocupados en el metal de la izquierda al mismo nivel que estados desocupados en el metal de la derecha y el efecto t�nel puede ocurrir, como se indica por las flechas. Es evidente que el n�mero de estados que quedan disponibles para el proceso dependen del voltaje aplicado, y si la probabilidad de tunelamiento es constante, como ocurre por voltajes aplicados muy peque�os, la corriente resultante var�a linealmente con el voltaje aplicado.

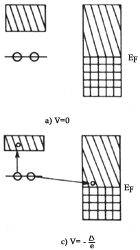
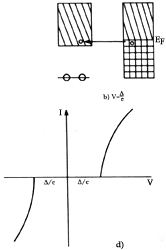
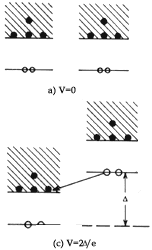
Figura XVII. Esquema que muestra el tunelamiento de electrones entre un metal normal y un superconductor. Las figuras a), b) y c) muestran las relaciones entre los niveles de energ�a a temperaturas muy cercanas a 0 Kelvin, para varios valores de la diferencia de potencial, V, aplicada al superconductor con respecto del metal normal. Si V es positiva el proceso de tunelamiento comienza cuando V alcanza el valor D/e, donde D es la anchura de la banda de energ�a prohibida y e es la magnitud de la carga de un electr�n, lo que se puede ver en la parte d) de la figura. Esto ocurre porque en estas circunstancias la parte m�s baja de los valores de las energ�as de los estados excitados de los pares de Cooper en el superconductor coincide con el nivel de Fermi del metal normal, como se muestra en la parte b) a partir de este momento es posible, para los electrones en el metal normal, pasar por tunelamiento a los estados disponibles en la banda de energ�a de estados excitados del superconductor. Al aumentar el voltaje aplicado al superconductor, aumenta el n�mero de part�culas que pasan a �l por el efecto t�nel. Si el voltaje aplicado al superconductor es negativo, el tunelamiento comienza cuando el voltaje alcanza el valor de -D/e. Aqu�, comienza a ocurrir un proceso nuevo, el rompimiento de un par de Cooper. Este proceso est� descrito en la parte c). Puede verse como un par de Cooper se rompe y uno de los electrones pasa por tunelamiento a un estado del metal normal por arriba de la energ�a de Fermi. El otro electr�n del par salta a la banda de energ�a prohibida del superconductor y queda en uno de los estados excitados. El n�mero de pares que pueden romperse de esta manera aumenta en relaci�n al voltaje aplicado. N�tese que una manera de medir la anchura de la banda de energ�a prohibida en el superconductor es midiendo el voltaje al cual comienza la corriente de tunelamiento. Hay que se�alar que a temperaturas mayores puede ocurrir que una corriente muy peque�a fluya para voltajes entre D/e y -D/e. Esto ocurre en virtud de que a estas temperaturas hay unos cuantos electrones excitados en estados por arriba del nivel de Fermi en el metal normal que pueden, si existe un voltaje positivo aplicado, pasar por tunelamiento a la banda de estados excitados del superconductor. Tambi�n existen por la excitaci�n t�rmica, algunos estados vac�os por debajo del nivel Fermi en el metal normal que quedan disponibles para el tunelamiento de los electrones del material superconductor que provengan del rompimiento de un par de Cooper, si existe un voltaje aplicado con un signo negativo. De cualquier manera, es muy marcado y notable el aumento en la corriente de tunelamiento cuando el voltaje aplicado es D/e o -D/e.

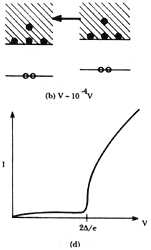
Figura XVIII. Tunelamiento de electrones individuales entre dos superconductores id�nticos. Las partes a), b), y c) muestran la relaci�n entre los niveles de energ�a. La parte c) muestra la corriente de tunelamiento electr�nico resultante. A temperaturas cercanas al cero absoluto el tunelamiento se da tanto de izquierda a derecha como de derecha a izquierda, de modo que no hay un flujo neto de corriente. Supongamos que ahora aplicamos un voltaje positivo al superconductor de la izquierda con respecto al de la derecha. El diagrama de energ�as del de la izquierda se va a desplazar hacia abajo con respecto al de la derecha, por el signo negativo de la carga electr�nica y por una cantidad de magnitud eV, como se ilustra en la parte b). Ahora tenemos un flujo neto de electrones por tunelamiento del superconductor de la derecha al de la izquierda, porque los electrones de la izquierda no tienen estados disponibles en el superconductor de la derecha a los cuales llegar por tunelamiento, en tanto que los de la derecha s� tienen estados accesibles en los de la izquierda a los cuales llegar por tunelamiento. La corriente aumenta con V hasta que los estados accesibles de la izquierda quedan por arriba de los estados ocupados por los electrones de la derecha, de manera que los electrones de la derecha ya no pueden pasar por tunelamiento a la izquierda. Puesto que las energ�as de todas las part�culas est�n dentro de un intervalo de K_BT,, a partir del nivel mas bajo, esta etapa se alcanza cuando eV ~ K_BT, o sea, cuando V ~ 10^-4 Volts. Si V se aumenta m�s, la corriente permanece pr�cticamente constante, porque los electrones que son capaces de pasar por el efecto t�nel, que son los que est�n en el superconductor de la derecha, permanecen constantes en n�mero. Sin embargo, cuando V alcanza la magnitud 2D /e, un proceso adicional, el rompimiento de un par de Cooper, empieza a ser posible, como se muestra en la parte c) de esta figura . Uno de los electrones que resulta del rompimiento del par puede pasar por tunelamiento al superconductor de la izquierda para ocupar el nivel mas bajo de la correspondiente banda de estados excitados. El segundo electr�n pasa a la parte mas baja de estados excitados del superconductor de la derecha. Como resultado de este proceso se tiene un flujo de electrones adicionales de derecha a izquierda y la corriente aumenta r�pidamente. Si V sigue aumentando mas all� de 2D/e, se sigue dando este proceso con la �nica diferencia de que ahora los electrones van a pasar a estados excitados. Existiran m�s combinaciones de estados excitados que pueden servir como estados finales y la corriente de tunelaje aumenta r�pidamente, como se indica en la parte d) de la figura. Cuando se tienen superconductores diferentes el proceso de tunelamiento es completamente an�logo.

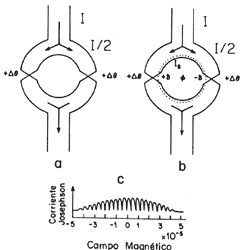
Figura XIX. Efecto Josephson. Cuando los pares de superelectrones (esto es, los pares de Cooper) pasan por el efecto t�nel a trav�s de una uni�n t�nel sumamente delgada, se da el efecto Josephson. Este resulta de la interferencia entre ondas macrosc�picas de corrientes superconductoras. Si se genera una corriente a trav�s de una uni�n t�nel sumamente delgada, las hondas superconductoras son coherentes, pero difieren por alg�n desfasamiento que depende del tama�o de la barrera t�nel. Hay dos efectos principales: el efecto dc y el efecto ac. En el efecto dc, una corriente dc fluir� a trav�s de la junta t�nel a�n en ausencia de voltaje aplicado o campo magn�tico aplicado. En el efecto Josephson ac, si existe un voltaje aplicado a trav�s de la uni�n t�nel, se observar�n oscilaciones de corriente de radio frecuencia (rf). Si se aplica un voltaje oscilante de radio frecuencia, se puede reducir una corriente dc. En la figura se presenta un diagrama del efecto Josephson: a) es una supercorriente, I, que se divide a trav�s de dos uniones y sufre un cambio de fase Dq , debido a un potencial aplicado. En b) el flujo magn�tico, f, induce una supercorriente adicional, I_s, que sufre un cambio de fase +d y -d en las uniones. En c) se tiene la medici�n de la supercorriente resultante en un SQUID de baja temperatura cr�tica, que muestra interferencia en el transporte de corriente.

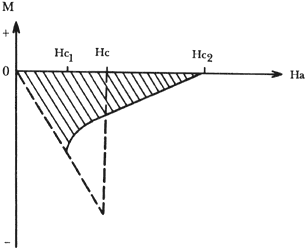
Figura XX. Esquema utilizado para definir un campo termodin�mico cr�tico para un superconductor tipo II. El tri�ngulo rect�ngulo se traza de manera que tenga un �rea igual a la parte sombreada dentro de la curva de magnetizaci�n. Es posible demostrar, por un c�lculo termodin�mico, que el trabajo hecho por el campo magn�tico sobre la muestra para magnetizarla cambia la energ�a libre del material al pasar del estado superconductor al estado normal y que se da por la diferencia entre las energ�as libres del estado normal y el estado superconductor. Este trabajo está dado por el �rea encerrada en la curva de magnetizaci�n y es (1/2) m_o H_C2V, donde V es el volumen de la muestra para un superconductor tipo I y H_C es el campo cr�tico. Esto tambi�n es v�lido para un superconductor tipo II, donde H_C queda definido a trav�s de esta figura.

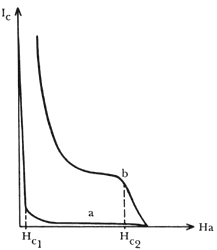
Figura XXI. Corrientes cr�ticas para alambres fabricados con un superconductor tipo II. La gr�fica a) se refiere a un alambre con muy pocas imperfecciones (muy pocas dislocaciones, vacancias, impurezas y cualquier otro tipo de imperfecci�n) y en el seno de un campo magn�tico aplicado a lo largo del alambre. La gr�fica b) se refiere a un material con un n�mero apreciablemente grande de imperfecciones y con un campo magn�tico aplicado perpendicularmente al alambre. En un campo magn�tico cuya intensidad es menor que el campo cr�tico, H_C1, un superconductor tipo II se encuentra completamente en un estado superconductor y se comporta como un superconductor tipo I. Cuando el campo aplicado es mayor que H_C1 pasa al estado mixto. El valor de la corriente cr�tica para campos menores que H_C1 queda determinado del mismo modo que para el caso de los superconductores tipo I, donde H_C pasa a ser H_C1. De hecho, esto ocurre as� s�lo en el caso de muestras que presentan muy pocas imperfecciones, como se ve en la parte a) de esta figura. De otro modo, se tiene el comportamiento mostrado en la parte b). Es un hecho ampliamente conocido que cuando un superconductor pasa al estado mixto, el valor de la corriente crítica est� controlado casi completamente por imperfecciones del material. Conforme más imperfecto es el material, más grande es el valor de la corriente cr�tica. Un alambre altamente imperfecto puede llevar hasta alrededor de 10⁵ amperios/cm². Rec�procamente un esp�cimen bastante perfecto tiene una corriente cr�tica peque�a, del orden de unos cuantos miliamperios/cm2, cuando se encuentra en el estado mixto. Esta dependencia de la corriente cr�tica con la imperfecci�n del material es de una importancia tecnol�gica muy grande, puesto que los electroimanes superconductores requieren alambre de resistencia cero y una gran capacidad de portar corriente, esto es, de una corriente cr�tica muy grande. Cabe se�alar que los nuevos superconductores cer�micos de alta temperatura corresponden a los superconductores tipo II.

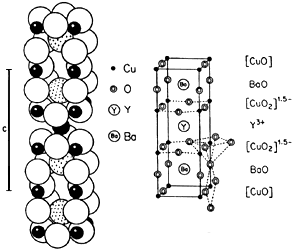
Figura XXII. Estructura cristalina del sistema Yba₂ Cu₃ O₇. Este compuesto se descubri� en un intento de reemplazar al lantano en el compuesto de La-Ba-Cu-O. Con otra tierra rara, el itrio (Y). Se observ� una temperatura de transici�n mucho m�s elevada, 93K. �ste fue el primer compuesto descubierto que ten�a una temperatura de transici�n superconductora por arriba de la temperatura de ebullici�n del nitr�geno l�quido. La figura muestra la estructura por capas del sistema Y-Ba-Cu-O, con el empaquetamiento (a) y la coordinaci�n (b).