INTERMEDIO
Omnívora
esfera
opaca, el tiempo fluye.
....
Tiempo
sin luz ni tacto.
....
¿En quién revienta esta luz?
CORAL BRACHO
(PARTICULARIDADES GEOMÉTRICAS)
EN ESTA segunda parte de mis apuntes, quiero inmiscuirme en algunas particularidades geométricas de los escenarios que escogimos. Pero si en las "Notas generales" di mis disculpas a los físicos, aquí tengo que prevenir a mis colegas, los matemáticos. Sacrificaré, en algunos pasajes, la formalidad y el rigor en aras de la exposición, la extensión y la claridad intuitiva. Además, siendo esto lo que más me duele, enunciaré por ahí algunos hechos como si fueran consumados, como si fueran verdades divinas, sin detenerme a cuestionarlos, argumentarlos y demostrarlos; la manera en que se hace de la matemática algo nuestro, terrenal, humano. Ni hablar, el espacio-tiempo de este libro es finito. Obligándome a dejar mis errores e inconsistencias para que el lector las detecte, las rellene y las lime como ejercicio.
Dedicamos una sección a cada espacio visitado en la Soñata.
En porciones pequeñas, el espacio proyectivo es como el nuestro (éste en el que vivimos). Se tienen en él las nociones de plano, de recta (o línea) y, por supuesto, de punto. Nociones que además están sujetas y se comportan de acuerdo con ciertas reglas mínimas o axiomas que se parecen mucho a los que Euclides usó hará más de dos milenios para definir y empezar a trabajar el plano y el espacio, que en su honor llamamos euclidianos; ese plano que medio vimos en secundaria, ese espacio en el que creemos vivir. Se tiene, por ejemplo, que (a1): por cualquier par de puntos pasa exactamente una línea, y (a2)por cualesquiera tres puntos no colineales pasa un único plano. Pero además, en el espacio proyectivo se cumplen:
(a3) Dos planos distintos se intersectan en una recta.
(a4) Un plano y una recta no contenida en él se intersectan en un punto.
(a5) Un par de rectas se intersectan si y sólo si están contenidas en un mismo plano, y en este caso, se intersectan en un único punto.
Éstos no son todos los axiomas que definen al espacio proyectivo, pero son los que usaremos aquí. Obsérvese, de los tres últimos, que en el espacio proyectivo, así como en el plano proyectivo (modelo teórico de cualesquiera de sus planos), no hay excepciones; es decir, que no existe la noción de paralelismo como la hay en sus versiones euclidianas. En el plano proyectivo, todas las rectas se intersectan igual: en un punto; y en el espacio proyectivo, planos y rectas se cortan siempre de la misma manera. ¿Cómo es esto posible?, se preguntará por ahí algún lector que aprendió a trazar paralelas. O "esto contradice a nuestra intuición y a nuestra experiencia", afirmará otro que cursó bien la secundaria, "es claro que hay rectas paralelas que nunca se cortan".
Reitero. El espacio proyectivo en pequeñas porciones es como éste. Nuestra experiencia del espacio en que vivimos está confinada a una porción minúscula de la Tierra, que a su vez es una minurria del Universo. Nuestra intuición del plano euclidiano se basa en esta hoja de papel o en un pizarrón o en una pared, que nos dan idea de cómo es él en una pequeña parte y, a la vez, en cualquiera de ellas. Esta intuición funciona igualito para el plano proyectivo; así como este cuarto nos da idea de cómo es el espacio euclidiano o el proyectivo o el Universo real (suponiendo su homogeneidad) en un entornito de cualquiera de sus puntos. Nuestra vivencia cotidiana no da elementos para afirmar si las "rectas paralelas" se juntan o no. Al adoptar un sistema axiomático, creamos un modelo teórico sobre el cual se puede trabajar con pasos firmes. Y no hay aún ninguna razón de peso para decidir si es el espacio euclidiano o es el proyectivo el que se asemeja más al real. Ambos son modelos teóricos, axiomáticamente consistentes, matemáticamente coexistentes, congruentes con nuestra experiencia cotidiana, y si el primero tiene preponderancia en la cultura popular como modelo del espacio en que vivimos se debe principalmente a su veteranía histórica. No hay más. Soltémonos el chongo un rato, y, de los axiomas que hemos enunciado, deduzcamos algunos hechos del escenario donde, por un ratito, metimos a vivir al niño.
Nos será útil, para la fluidez del texto y la concreción de las ideas, introducir algo de notación. Sea P3 el espacio proyectivo, y análogamente, sean P2 y P1 el plano y la recta (o línea) proyectivos respectivamente (modelos teóricos que podemos pensar como cualquier plano, o recta, de P3 ). Obsérvese que los superíndices denotan dimensión y no exponenciación, se lee por tanto "P-tres" en lugar de "P-cúbica" o "P-a-la-tres". Análogamente, se usará más adelante la notación E3 , E2 y E1 para el espacio, el plano y la línea euclidianos.
Veamos primero cómo es una recta proyectiva. Para esto, tomemos a P2
, pensando que esta hoja es una porción de él, de cualquier plano de P3. Tomemos
el punto p de la figura, y una línea l que no lo contenga; de
l sólo vemos un pequeño cachito, pero queremos averiguar cómo es.

Figura 2. Una línea y un punto fuera de ella.
Sea Lp el conjunto de rectas en el plano que pasan por p;
el haz de rectas por p, podríamos llamarlo. El axioma (a5)
implica que todas estas rectas intersectan a l en algún punto. Hagamos
corresponder a cada línea de Lp su punto de intersección en
l. El axioma (a1) nos dice que por cada punto de l
pasa una única recta de Lp (la que también contiene a p),
implicando que la correspondencia entre Lp y los puntos de
l es biunívoca.
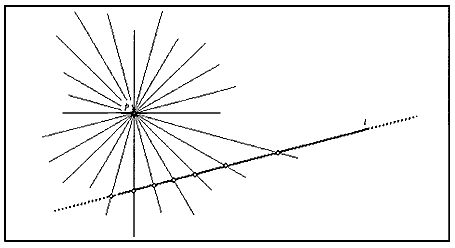
Figura 3. Los puntos de una recta y las rectas por un punto, fuera
de ella, se corresponden biunívocamente.
Tomemos ahora una línea l0 Î Lp.
Y sea p0 su punto correspondiente en l, es decir, p0
= l0 Ç l *![]() Al
girar lentamente a l0 (como si
p fuera una tachuela atravesándola, para que se mueva en Lp),
el punto correspondiente, p0 , se va deslizando continuamente
en l: se saldrá de nuestra figura en poco tiempo, pero hemos demostrado
que sigue su camino a lo largo de l. Detengamos el giro al llegar a 180°.
Al
girar lentamente a l0 (como si
p fuera una tachuela atravesándola, para que se mueva en Lp),
el punto correspondiente, p0 , se va deslizando continuamente
en l: se saldrá de nuestra figura en poco tiempo, pero hemos demostrado
que sigue su camino a lo largo de l. Detengamos el giro al llegar a 180°.
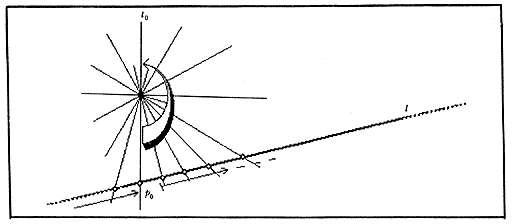
Figura 4. Al viajar un punto por una recta proyectiva, regresa por
el otro lado.
Observemos que l0 está en su posición inicial; aunque se haya "invertido en p", es ahora la misma recta con la que empezamos. Además, hemos barrido al haz de rectas Lp; es decir, salvo por l0 donde comenzamos y acabamos, pasamos por todas las rectas de Lp, y sobre cada una un solo instante. Por tanto, p0 recorrió toda la recta l para regresar a sí mismo por el lado opuesto a su partida. Y esto lo hizo en un tiempo finito (¿por qué?).
Esto es suficiente para explicar la "visión de la caverna". Cerremos un ojo
(me refiero al de WTo, nuestro personaje inmerso
en el espacio proyectivo). Pongámoslo en reposo. ¿Qué ve?
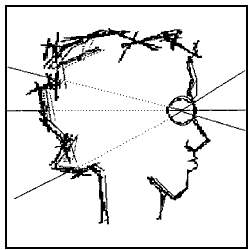
Figura 5. En cada dirección se percibe la superficie del cuerpo en
dirección opuesta.
Sea p0 el foco del ojo abierto. Por la línea l, que sale de p0 , va a recibir los estímulos luminosos que hayan salido de puntos en l y que viajen por esta línea recta. Siguiéndola como en el párrafo anterior, vemos que el primer objeto material con que se topa esta línea l es la propia cabeza de WTo, poco antes de que p0 regrese a sí mismo por el lado opuesto. Por tanto, en la dirección de l y hacia adelante, hay que especificar —en la dirección d, digamos—, WTo observa el punto en que abandona su cuerpo un rayo saliendo de p0 en la dirección opuesta a d, punto también de la recta l.
ÓPTICA TRIDIMENSIONAL EN EL ESPACIO PROYECTIVO
Todos hemos oído que el tener dos ojos, la estereovisión, nos permite percibir
la tridimensionalidad del mundo en que vivimos. Veamos brevemente cómo funciona
este mecanismo, para observar después los problemas que acarrearía al trasladarlo
tal cual a un espacio proyectivo chico ("la caverna"), y concluir con el modelo
óptico que, para la percepción tridimensional, hemos adoptado al producir la
Soñata.
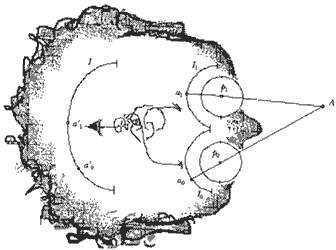
Figura 6. Percepción tridimensional con estereovisión. La separación
de las imágenes produce la sensación de cercanía.
Tomemos una sección plana de una cabeza que incluya a los dos focos de los ojos que numeraremos 0 y 1. Supongamos que tomamos la sección horizontal para fijar ideas, aunque funcione igual para cualquier otra. Sean p0 y p1, estos dos puntos, los dos focos; véase la figura, donde hemos abstraído el portento lenticular de un ojo, adoptando un modelo simplificado: la retina percibe únicamente los rayos que pasan por el foco de su ojo para formarse una imagen del exterior; sean I0 e I1 , correspondientemente como en el resto de la notación, estas imágenes, que podemos pensar como placas fotográficas fijas en un círculo máximo de una esfera (su ojo). Sea A un punto visible, y sean a0 y a1 , sus imágenes. Tenemos un mecanismo, integrado en las conexiones neuronales de nuestro cerebro, que conjuga las dos imágenes; proceso que podemos pensar como volver a invertirlas y sobreponerlas en una nueva imagen I, "la pantalla en el cerebro" que hemos amplificado en la figura. Y ahora: según qué tan lejos queden los destinatarios en I de a0 y a1 , denotados a0' y a1', nos indica qué tan cerca está el punto A de donde provienen. Para convencerse, juegue el lector un rato a mover el punto A; o el dedo gordo enfrente, mientras cierra y abre alternadamente los ojos enfocando al infinito.
Veámoslo con más detenimiento. Sean a0
y a1
los ángulos que forman los rayos de A a los focos p0
y p1 con el segmento
que une a estos últimos (figura 7); información equivalente a a0
y a1 , nótese, y que además
determina a A. Al acercarse A, los ángulos decrecen; y al alejarse
A, aumentan, aproximándose al límite (que nunca se alcanza en el espacio
euclidiano) de que su suma llegue a 180° (cuando los rayos que inciden en
los ojos son paralelos, A está en el infinito)
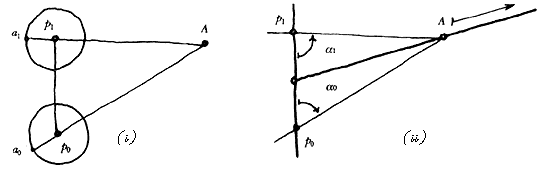
Figura 7. Al alejarse A, la suma de los ángulos aumenta.
Ésta es la teoría, pero en la práctica, llegar a 180° es más bien algo que se le parezca, dependiendo de la precisión del cerebro y de la vista; para el común de los mortales si A va media cuadra adelante o una entera, no se nota. Es decir, la estereovisión funciona hasta el punto en que el procesador no distinga entre a0 + a1 y 180° y, considerando que la distancia entre los focos de la cabeza en cuestión es como 5 cm, ya de por sí sobrecargados, no le podemos pedir mucho a nuestro cerebro. Para distancias cortas el mecanismo de la estereovisión funciona de maravilla, pero llegado un punto —que está, a campo abierto, como a 100 o 200 metros de nosotros, para ser muy generosos; o, que es su propio foco para un tuerto—, punto que llamaremos nuestro infinito visual, denotémoslo -¥v, tendremos que, o bien mirar con sumo cuidado, o bien usar mecanismos alternativos para la percepción tridimensional. De éstos contamos, por ejemplo, con: la comparación del tamaño del objeto real que ahí intuimos; o la simple referencia al piso —"que vemos algo en un arbolito: pues lo relacionamos por el tronco con el piso esperando saber nuestra distancia a la raíz"— no nos dice rápido qué tan lejos está. Una afortunada combinación de estos procesos nos ofrece esas hermosas salidas de inmensas lunas gordas tras horizontes crepusculares y cercanos, íntimos: al no distinguir los infinitos del horizonte y la luna, jalamos a ésta a la distancia de lo que sí conocemos, y, puesta entonces sobre una casa, nos la queremos comer. (Quien haya tomado, ilusionado, una foto de este espectáculo habrá sentido la necesidad de la pintura para expresarse tras los decepcionantes resultados.)
Introduzcamos ahora el mecanismo de la estereovisión en el espacio proyectivo, fijando de nuevo un plano P2, donde seguimos teniendo la información local de las figuras anteriores, y que podemos condensar en la siguiente, la cual se ha indicado por o al punto medio del segmento que une a los focos de los ojos ( p0 y p1).
Como esta hoja es un buen modelo de lo que pasa en porciones chicas de P2,
el mecanismo vuelve a funcionar de maravilla cuando A, el punto luminoso
que andamos acarreando, está cerca de la cabeza. Pero ahora alejémoslo, en la
línea recta l que une a o con A. Hemos visto que, en este
viaje, A regresará a o por el lado contrario. Considérese a
A', cercano a este retorno. Y obsérvese que los ángulos correspondientes,
a0' y a1',
suman algo peligrosamente cercano a 360°. Como esta suma ( a0
+ a1) partió de algo cercano
a cero y ha crecido conforme al viaje de A, podemos concluir que en algún
punto estuvo justo en 180°. Llamemos a este punto el infinito de o en
la recta l, denotándolo ¥ (o, l).
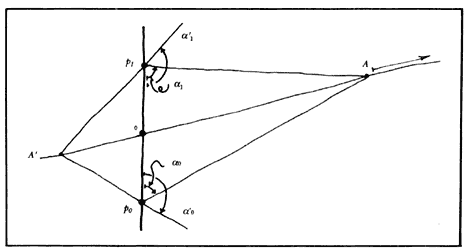
Figura 8. En el espacio proyectivo, al alejarse A, se aproxima
a su punto de partida. Sea A' cercano a este retorno.
Demostremos que ¥(o,l) solamente depende de l y no de la dirección en que se alejó A, girando la figura 9(i) 180° alrededor de o, y observando que cae sobre sí misma. Por tanto, esta transformación de P2 (la rotación) tiene que dejar fijo a ¥ (o,l) pero ha intercambiado las direcciones de l en o. ¿Puede el lector demostrar que el efecto de esta rotación en la figura 9(ii), que retrata la situación cerca de ¥ (o,l) , es reflejar en la perpendicular a l?. Pero observemos además que el triángulo D = ( p0, p1, ¥(o,l)) que contiene a A, ha caído sobre D' = ( p0, p1, ¥(o,l)) conteniendo a A'; por tanto, los segmentos que unen a o con su infinito en la línea l, y que juntos la cubren, miden lo mismo; es decir, la distancia de o a ¥ (o,l), llamémosla r, se realiza por los dos segmentos en que se parte la única línea que los une, l.
Este número r es una constante del espacio proyectivo al que nos hemos
metido, su radio. Es la distancia máxima a la que pueden estar dos puntos
de él. Si el radio del P3 en que estamos rebasa nuestros límites
perceptivos, no tendríamos mayor problema. Pero recordemos que hemos metido
a un niño en un P3 con volumen comparable al de este cuarto,
con sus radios iguales, digamos. Nos hemos inmiscuido entonces en algo comprendido
dentro de la esfera de su infinito visual para la estereovisión cotidiana. ¿Qué
sucede entonces?
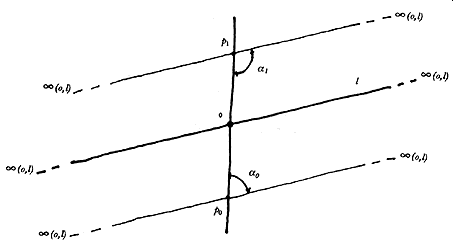
Figura 9.i. Cuando A llega al infinito de o en l
(a0+a1=
180° ).
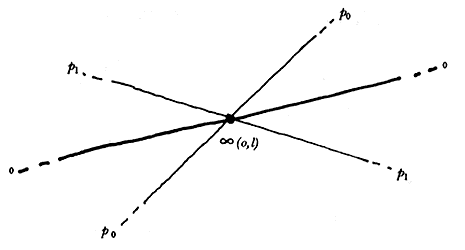
Figura 9.ii. Retrato de ¥ (0, l).
Pensemos de nuevo en nuestro ayudante luminoso, el punto A, poniéndolo justo en ¥ (o,l) Dando media vuelta a la cabeza con centro en o, observamos su otra imagen, A', que en realidad es el mismo punto. Sabemos que ambos están a la mismita distancia de nosotros, dos o tres metros. Pero nuestro mecanismo de estereovisión los pondría en nuestro infinito visual, ¥v, pues los ángulos que se forman suman 180°. De haberse alejado A continuamente de nosotros para posarse en ¥(o,l), habríamos sentido que aceleraba rápidamente hasta situarse en el infinito, o en la zona donde deja de servir nuestro procesador de distancias. De haber recubierto A con una pelota de goma mascada, se hubiera convertido, en este simple viaje, en una inmensa Luna gorda, con su lado oculto expuesto en la dirección contraria. Contengamos la tentación de alejar A un poquito más para explorar otro poco al infinito de o.
Hemos hablado del infinito de o en la recta l, pero notemos que la línea l fue escogida arbitrariamente. Tenemos entonces para cada l que pasa por o un infinito. Sea ¥(o) el conjunto de todos estos puntos; podemos escribir
donde Lo es el haz de rectas que pasan por o (la diferencia con el Lp que consideramos al principio es sólo que ahora estamos en P3 y el punto en cuestión es o). Por lo que ya sabemos, ¥(o) se podría también definir como el conjunto de puntos a distancia r de o. Resulta que ¥(o) es un plano de P3 , que no tiene nada de especial, es como cualquier otro plano, simplemente le corresponde a o; pero si movemos o, su plano al infinito también se moverá.
Para demostrar que ¥(o) es efectivamente un plano de P3 , consideremos dos puntos en él: p = ¥(o,l) y p' = ¥(o, l'). Y ahora rotemos al plano generado por l y l', 180— alrededor de o. Esta rotación deja fijo a p (argumentación que sigue a la figura 9), pero entonces también deja fijo a p' (y a todos los infinitos de o en ese plano pues la rotación sólo depende de o y el plano); luego entonces deja fija a la recta que pasa por p y por p'. Por otro lado, como la rotación intercambia los rayos que salen de o con sus opuestos y preserva distancias, si deja fijo a un punto distinto de o, los rayos de o a él en ambas direcciones miden lo mismo, es decir, están en ¥(o). Esto demuestra que la recta por p y p' está contenida en ¥(o); que es la recta al infinito de o en el plano considerado. Tomando un nuevo punto p"Î¥(o), se concluye de lo anterior que el plano generado por p, p' y p" es ¥(o).
Regresemos a la estereovisión en P3. Recordemos (figura 6) que desde nuestro origen perceptivo o, observábamos por enfrente a A, un punto luminoso, que alejamos hasta ¥(o,l) (figura 9). Si alejamos A un poquito más, experimentamos algo completamente nuevo para nuestra máquina perceptiva: que el estímulo luminoso que recibimos de un mismo objeto, llega por rayos que, saliendo de nuestros dos ojos, se separan (a0+a1 ha rebasado los 180°). Siendo ésta la primera vez que el cerebro enfoca en algo que produce este efecto, la luna-pelota se separaría en dos imágenes superpuestas (enfóquese en el pulgar cercano y obsérvese cómo el horizonte se separa en dos).
Recordemos, además, que al momento de abrir los ojos por primera vez, el niño de la Soñata ve puntos cercanos a o (su cabeza), pero por "el otro lado", cuando la suma de ángulos se aproxima a 360° (A' en la figura 8). Y, a primera de cambios, no podemos esperar que su cerebro decodifique esta información contradictoria. Por tanto, lo hicimos ver borroso, ver cuatro orejas. Pero al cerrar un ojo, la imagen es nítida, aunque plana. Nos deja así en el dilema de cómo hacer que perciba tridimensionalmente.
Las células de la retina son capaces de medir la intensidad, la luminosidad
del estímulo que las excita (no es lo mismo ver un foco a 3 metros que a 10
centímetros). Teniendo el cerebro la información adicional de haber visto una
cabeza a 10 cm de distancia, no es descabellado asumir que pueda interpretar
la diferencia (o el cociente) entre la luminosidad aparente (medida en el momento
y en la célula correspondiente) y la luminosidad real (archivada en la memoria)
como indicador de la distancia que ha viajado el estímulo. En otras palabras,
si un punto, prendido como foquito de luminosidad constante, se va alejando,
excitará cada vez menos a las células correspondientes, y de esta variación
podemos deducir su distancia. Así, interpretando adecuadamente los rayos lumínicos
que pasan por el foco de un solo ojo, el cerebro se puede formar una imagen
tridimensional. (Por cierto, según mi asesoría astronómica, de un análisis similar
al aquí propuesto se deduce la distancia de los cuerpos celestes.)
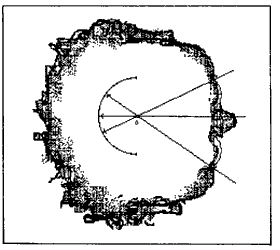

Figura 10. Se interpretan únicamente los estímulos que pasarían por
el origen perceptivo.
Para acabar de precisar el modelo óptico de la Soñata, tomamos como foco no al de un ojo, ni al punto medio de ambos, sino que lo empujamos hacia adentro un poco, internándonos hasta la línea de las orejas, hasta un punto en el centro del cráneo del personaje, punto que, en las "Notas generales", ya habíamos bautizado como o, el origen perceptivo de WTo. Y suponemos que la imagen tridimensional que se forma en el cerebro toma en cuenta únicamente a los rayos que pasarían por o, analizando puntualmente sus propiedades. Cuando el niño se puso a jugar a abrir y cerrar alternadamente los ojos para ver, con interés, cómo brincan las cosas de lugar, asumimos que su aparato perceptivo (ojos, lentes, músculos, retinas, cerebro e inclusive piel) estaba aprendiendo a simular este proceso con cierta precisión. Quizá suene biológicamente descabellado, pero concuerda con nuestra percepción cotidiana del mundo y es justo el modelo con el que estudiamos al Universo real; salvo que en este caso —algo aún más descabellado— todos los procesos se llevan a cabo en el mismísimo o, el foco, la Tierra.
Habiendo, entonces, logrado que el niño vea en su caverna, lo dejamos ahí, jugando y gozando un rato más con su geometría.
(Primer escenario del Tiempo II)
Para adentramos con mayor libertad en el toro tridimensional, o espacio toroidal, nos será de gran utilidad describir y definir nuestro espacio perceptivo.
Construyámoslo basados en una famosa observación de Descartes con evidente
trasfondo griego.Observemos primero que la línea euclidiana, E1,
se corresponde con los números. Para esto, se toma uno un origen o en
E1 y se escoge, además, algún otro chalán para que la haga
como 1. El segmento de 0 a 1 la hará entonces de "metro", de vara de medir;
la jalamos para que reinicie en 1, y donde caiga, ponemos al 2; lo hacemos otra
vez, igual con el 3; y le seguimos otro rato hasta que nos damos cuenta de que
podríamos seguir por siempre. Entonces le paramos y eso decimos. Podemos embelesarnos
con esto un rato, hemos descubierto a los números naturales, esos que
sirven para sumar y multiplicar, que usamos para mercar, esos que aguantan cualquier
inflación; y soñamos en restar. Regresemos al origen para observar que queda
una mitad de línea totalmente vacía; tendemos en ella, con varita de medir en
mano, a los números negativos. Así, hemos puesto en E1 a los
números enteros; esos que sabemos sumar al grado de incluir a la resta;
esos que sabemos multiplicar, aunque prometo no abusar de esta complicadísima
operación en estas notas; esos que tantas y tantas ensoñaciones matemáticas
han causado; los denotaremos como Z; usanza tradicional y universalizada
que no sé de dónde proviene.
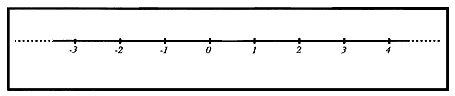
Figura 11. Los números enteros en la recta euclidiana.
Quedan aún grandes huecos en E1; partimos entonces nuestra
vara en partes iguales y metemos a todos los racionales; ya sabemos dividir.
Pero aún quedan hoyos, que ya no son tan fáciles de detectar; números hermosos
como ![]() , la diagonal de
un cuadrado hecho con nuestra varita (el primer irracional en descubrirse) o
p, lo que recorre el 1 al girar la varita media vuelta alrededor de 0.
Y aquí, hay que invertirle un poco más de coco y tiempo para entender —si
es que se puede— lo que está pasando. En fin, los números reales se pueden
pensar como la recta euclidiana E1, sus elementos o puntos
se corresponden, simbiotizándose en la recta real R; un continuo unidimensional
ideal, ricamente algebraizado.
, la diagonal de
un cuadrado hecho con nuestra varita (el primer irracional en descubrirse) o
p, lo que recorre el 1 al girar la varita media vuelta alrededor de 0.
Y aquí, hay que invertirle un poco más de coco y tiempo para entender —si
es que se puede— lo que está pasando. En fin, los números reales se pueden
pensar como la recta euclidiana E1, sus elementos o puntos
se corresponden, simbiotizándose en la recta real R; un continuo unidimensional
ideal, ricamente algebraizado.
Llegó entonces Descartes y observó que de aquí se concluye que los puntos del
plano euclidiano E2 corresponden a parejas ordenadas de números
reales. Esto se sigue del axioma de las paralelas; el célebre quinto postulado
de Euclides, el que no vale en el plano proyectivo, el que hace excepciones,
el que dice que dados una línea l y un punto p, existe una única línea 1(p)
paralela a 1 y que contiene a p; donde hemos convenido en que una recta
es paralela a sí misma, es decir, que dos rectas son no paralelas cuando se
intersectan (en un único punto). Para ver cómo razonó Descartes, tómense dos
rectas en E2 , l0 y l1
, no paralelas. Dado cualquier punto p Î E2,
sean p0 = l0 Ç
l1 (p) y p1 = l1
Ç l0 (p).Y al revés, dados
p0 Î l0 y p1
Î l1 , sea p = l1
( p0 ) Ç l0
( p1). Es fácil deducir de los axiomas que hemos
establecido una correspondencia entre E2 (sus puntos) y parejas
que constan de un punto en l0 y otro en l1
; pero ya habíamos visto que tanto l0 como l1
se pueden poner en correspondencia con R.
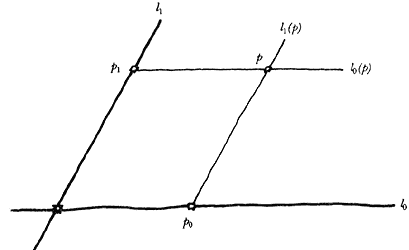
Figura 12. Los puntos del plano euclidiano corresponden a parejas
de puntos en dos rectas no paralelas.
La usanza común para hacer explícita esta correspondencia, y que aquí adoptamos
por simplicidad, es tomar ortogonales a las rectas, superponer los orígenes
en la intersección y medir en ambas con la misma vara. Pues entonces las fórmulas
algebraicas —que presionan para aparecer en escena, aunque intentaremos
mantenerlas a raya— se nos simplifican bastante. Por ejemplo, la distancia
—medida con la vara escogida— de cualquier punto p al origen
o, queda determinada por el teorema de Pitágoras:
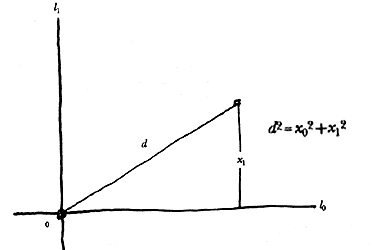
Figura 13. La distancia de un punto al origen en función de sus coordenadas
cartesianas.
donde x0 y x1 son los números reales que corresponden a p.
Cuando las frases se nos van haciendo demasiado largas, es tiempo de introducir notación. Dados dos conjuntos X y Y, sea X x Y el conjunto producto cartesiano de X y Y, que consta de las parejas de elementos formadas por uno en X y otro en Y; es decir, la pareja (a, b) Î X x Y si y sólo si a Î X y b ÎY; o bien
Es claro que podemos tomar productos cartesianos cuyos factores a su vez son productos cartesianos. Y ésta es la maravillosa implicación a la observación de Descartes. Ya que conocemos R y R x R rápido reconocemos a R x R x R como el espacio que percibimos; y nos aventuramos a trabajar con R x R x R x R, pero nos damos cuenta de que podemos seguir por siempre; lo decimos, y denotamos con Rn a R x R x ... x R cuando el factor se repite n veces. Nótese que el superíndice aquí sí denota exponenciación (con el producto cartesiano), correspondiendo además a nuestra idea intuitiva de dimensión. Hemos encontrado la manera de entrar a un espacio n-dimensional, de trabajar en él, con él. Pero no nos asustemos. Aquí no pasaremos, en un buen tiempo, de cuatro.
Por el momento sólo nos interesa el tres. Hemos demostrado que ![]() (donde
(donde
![]() denotará una correspondencia
biunívoca —correspondencia, simplemente, le llamamos arriba— entre los
conjuntos X y Y.) Hemos visto también, en el caso del plano, que
denotará una correspondencia
biunívoca —correspondencia, simplemente, le llamamos arriba— entre los
conjuntos X y Y.) Hemos visto también, en el caso del plano, que
![]() , y por tanto, que
, y por tanto, que ![]() .
Y ya con este vuelo, se demuestra el análogo en dimensión tres,
.
Y ya con este vuelo, se demuestra el análogo en dimensión tres, ![]() ,
pero fácil.
,
pero fácil.
Definamos que el espacio perceptivo de WTo es R3; trabajar con números reales, aunque nos los entreguen en ternas, nos hace sentir una herramienta algebraica poderosísima a nuestro alcance. O lo podemos pensar también como el espacio euclidiano tridimensional, E3, ese vacío ideal en toda su serenidad griega, con un foco prendido, el origen perceptivo o, y una vara de medir en la mano. Cuando queramos ponernos el espacio perceptivo en nosotros mismos, situemos el origen o = (0, 0, 0) en el centro del cerebro, que el primer 1 quede hacia enfrente por la entreceja, el otro en alguna oreja, al gusto de orientación del sujeto, y el 1 faltante arriba; así, sabremos llegar a cualquier punto x del espacio perceptivo tan pronto nos den sus coordenadas x = (x0, x1, x2). No necesariamente hay que llegar a él, sabemos que ahí está, y lo denotaremos simplemente como x mientras nos sea posible.
EL TORO TRIDIMENSIONAL; SU TOPOLOGÍA
Otra gran puerta que nos abre la observación de Descartes es la de jugar con productos cartesianos de conjuntos o espacios varios para formar otros nuevos. Tomemos, por ejemplo, los siguientes espacios, o dibujos, poco dimensionales:
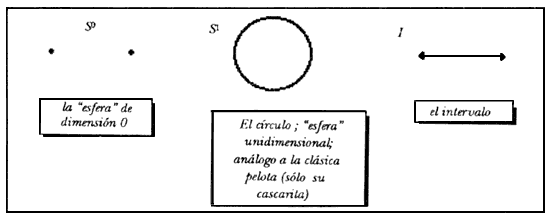
Figura 14. Espacios sencillos de dimensión 0 y 1.
para luego combinarlos:
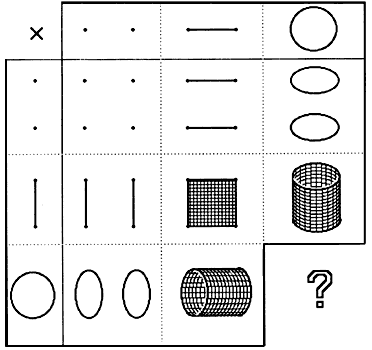
Figura 15. Tablita de multiplicar con el producto cartesiano y espacios
de dimensión 0 y 1.
Así, vemos por ejemplo que S1 x I se puede interpretar como un círculo de intervalos, o bien un intervalo de círculos; el conocido "cilindro", el siempre bien ponderado "tubo".
Y, de aquí en adelante, nuestro interés se dirige hacia el toro, llamado así por los griegos: el círculo de círculos (los meridianos o paralelos —da lo mismo— en el siguiente dibujo: gírese un aro vertical una vuelta entera en su plano horizontal).
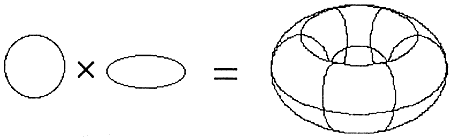
Figura 16. S1 x S1 =
T 2.
Para el lector que siga dudando de la última figura, sale otro argumento. Obsérvese
que el círculo se puede pensar como el intervalo identificando sus extremos,
es decir, decretando al 0 y al 1 (extremos de I) como el mismo punto;
esto lo denotamos S1 =I/{0 ~ 1}, leyendo "I módulo
(o sobre) la relación: 0 equivalente a 1". Y por tanto, el toro se obtendrá
del cilindro identificando sus extremos, pegando sus dos bordes, simbiotizando
sus bocas, es decir, S1 x S1 = S1
x I/{(p, 0) ~ (p, 1). Análogamente (ver figura 15), el
cilindro se obtiene del cuadrado al identificar dos lados opuestos, S1
x I= I x I/{(0,x) ~ (1, x)}; o bien, el toro
se obtiene del cuadrado al identificar, por parejas, sus lados opuestos S1
x S1 = I x I/{(x, 0) ~ (x, 1)},
{(0,x) ~ (1,x)}.
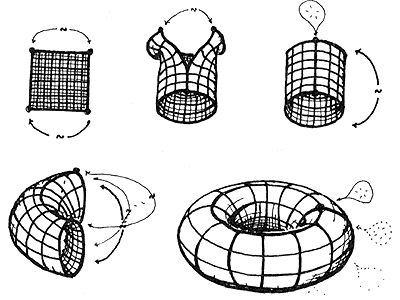
Figura 17. El toro (S1 x S1) se obtiene identificando lados opuestos
de un cuadrado, pues S1 se obtiene de I, identificando extremos.
Definimos finalmente al toro tridimensional como:
el espacio de tripletas cuyas tres coordenadas son puntos de un círculo. Ya no podemos hacer un dibujo de él, pero hemos metido ahí un joven personaje para que lo viva y nos relate su experiencia.
Para entender la visión, la imagen que tendríamos al estar solos en T3, estudiemos primero a sus hermanos pequeños, T2 = S1 x S1 en dimensión dos, y en una, S1, un solo factor, que coincide también con P1 , nuestra conocida línea proyectiva.
Consideremos a un ser perceptivo e inteligente —tanto como podamos—
de dimensión 1. Será un sólido unidimensional, es decir, un intervalo a quien
llamaremos —o— para dibujarlo —o—, y de quien
nos interesa principalmente su origen perceptivo o, situado en su centro: su
punto medio. Metámoslo a vivir en S1 . Hemos visto que si
su radio de percepción es menor que la circunferencia de su universo, se sentirá
en una recta que asumirá infinita y que identificará con R por las distancias
que puede, en principio, viajar. Pero si su radio perceptivo aumenta, hasta
sobrepasar de plano al radio de su universo, se sentirá encerrado en algo que
corresponde a la frontera de su cuerpo (recuérdese la caverna). Llamemos
menos y más a sus extremos: (-)—o—(+). Por la dirección menos
recibirá un estímulo más y viceversa. Se formará entonces la siguiente imagen:
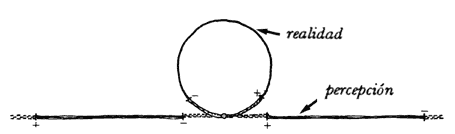
Figura 18.—o—, su universo y su espacio perspectivo.
Llamemos instante al tiempo que tarda la luz —un estímulo— en atravesar a este universito. Los movimientos o señales que manda nuestro ser inteligente tardarán entonces cerca de un instante en ser "repetidos" por la imagen correspondiente.
Démosle ese instante para pensar, y, por un momento, démosle también más cancha a nuestro ser aumentándole su dimensionalidad. Pero controlándolo, dejando trivial, chiquita, infinitesimal, a la segunda dimensión. Hagámoslo usar su nueva cancha, bajándole el volumen a la luz, a su velocidad, e involucrémoslo, fintando a su caverna, su menos vecino. Le hemos dado espacio suficiente para que serpentee, abandonando su mundo, medio instante antes de retornar a él, reposado, observando atento por su frente, su más. Llegado el instante, el menos que ve se desvanecerá y descubrirá un nuevo menos, al doble de la distancia aproximadamente: al abandonar por completo su universo, o serpentearlo simplemente, pero acoplado al ritmo de la velocidad de la luz; la luz que recibiría de su menos por su más ha pasado de largo; al concluir el instante recibe de lleno un estímulo que ha dado dos vueltas al universo.
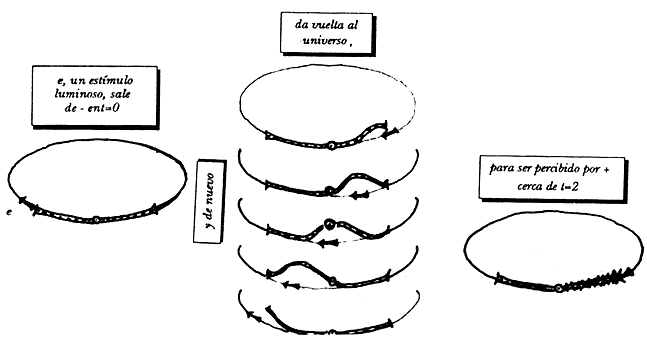
Figura 19. —o— se percata de un equivalente a distancia
2.
Pensemos el serpenteo como un volverse transparente. Si nos transparentamos poco más de un instante, percibiremos un tercer menos —y un tercer más en la dirección opuesta—, pues los primeros dos se transparentarán el tiempo suficiente para traslaparse en el acto; y así, tras unos cuantos experimentos con mensajes inteligentes, aprendiendo a serpentear y a percibir los serpenteos, concluiríamos que en nuestro espacio hay un ser equivalente a nos —o—tros para cada entero nÎZ, llamémosle —n—, repitiendo nuestro comportamiento de hace [n] instantes (donde [n] denota magnitud de n, la distancia al origen, nunca negativa); aunque para comunicarnos con —n— tengamos que poner de acuerdo a sus anteriores (n - 1) chalanes, ahí está, ahí lo tenemos. En nuestro espacio perceptivo R, parametrizándolo en instantes-luz (es decir, midiendo las distancias con lo que viaja la luz en un instante, con la circunferencia del universo, la distancia al centro del vecino), pondríamos a —n—, centrado en su correspondiente punto de R, su distancia dirigida, quedando nosotros situados en el origen o, dándole su tiempo y su ritmo al transcurrir de este universo —corriendo el peligro de caer en la tentación del "Line-King" de Abbott, del pequeño tirano de Lineatitián, hubiésemos dicho en el capítulo 5: la tentación de creerse "el rey", y seguir siendo sólo uno, y todos los demás, bien comandados, sirviendo, complaciendo.
(¿Puede el lector describir qué pasaría si el niño de la caverna tuviera la capacidad de hacerse transparente y jugara con ella; qué idea de su universo se formaría?)
Hemos dado cuenta de Z Ì
R; y completaríamos la imagen de nuestro espacio perceptivo al darnos
cuenta de que entre cada par de imágenes nuestras consecutivas, entre —n—
y —(n + 1)—, hay un espacio que las separa, un intervalo vacío
equivalente al que tenemos en cualquiera de nuestros lados, dependiendo sus
longitudes exactas del movimiento que hayam—o—s realizado en
el pasado correspondiente. Pensaríamos entonces que nuestro universo es una
recta, correspondiendo sus puntos a potenciales emisores de estímulos. Estaríamos
parcialmente en lo cierto. Pero dejemos ya al "gusanit—o—" regocijándose
en la inmensa y tumultuaria imagen de su minúsculo y desolado universo, abstraigámoslo
de él quedándonos únicamente con sus puntos y un origen. De un mismo punto,
pÎS1 , o puede recibir estímulos
por diversas trayectorias, pero no de manera arbitraria, ciñéndose éstas a una
lógica precisa.
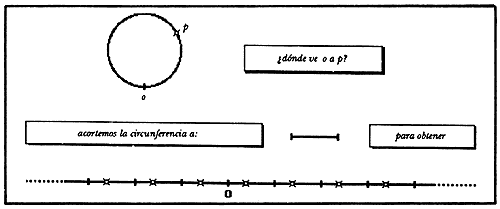
Figura 20. Donde o representa las posibles imágenes de p siendo
o = o.
Podemos agrupar a los números reales de acuerdo con su posición relativa respecto
a los enteros. La recta real R se parte, al subrayar a los enteros Z,
en intervalos equivalentes. Cualquiera de ellos podría obtenerse al sumarle
un entero adecuado a cualquier otro (transladarlo); todos ellos imagen fiel
del intervalo [0, 1] = I, del cual se obtiene el círculo S1
al identificar los extremos (los enteros que caen en él). Una visión más acertada
de S1, en cuanto a la homogeneidad o continuidad que proporciona,
será entonces la de los números reales R, identificando a dos de ellos,
x y x' digamos, cuando guardan la misma relación con los enteros,
cuando difieren por uno de ellos, es decir, cuando x - x'ÎZ
podríamos escribir S1 = R/{ x ~x'; x-x'Î
Z }, esto es, el círculo son los reales al identificar dos de ellos siempre
y cuando su diferencia sea entera.

Figura 21. Se identifican dos puntos cuando su distancia es entera.
A esta identificación la simulamos cada vez que enrollamos una cuerda. Sólo
su tridimensionalidad nos impide hacerlo idealmente: si enrollamos la recta
real sin alterar sus distancias sobre un círculo de circunferencia unitaria,
caerán entonces todos los enteros sobre el mismo punto, o, y cada
real guardará su posición, relativa a ellos; lo que equivale a poder guardar,
idealmente, series de foquitos de Navidad.
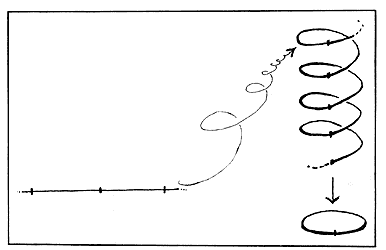
Figura 22. La recta real cubriendo homogénea, isométrica e indefinidamente
al círculo.
Paréntesis algebraico. Hemos hecho uso de una "relación de equivalencia" en los números reales, refiriéndolos, por medio de la suma, a los números enteros. Este es un caso particular de una operación que relaciona grupos con grupos a través de subgrupos que valdrá la pena fijar en abstracto en el caso abeliano.
Sea G un grupo abeliano, es decir, un conjunto con suma; donde esta suma es conmutativa, tiene su cero y da cuenta de su resta (piénsese en los números reales). Y sea H un subgrupo de G, es decir, los de H se bastan entre ellos con la suma de G para formar un grupo propio, sumándose y restándose por sí solos (piénsese en los enteros). Decimos que dos G-itas g y g', es decir, g, g' Î G, son equivalentes módulo H, escrito g ~ g' (mod H), siempre y cuando difieran por un H-ita, esto es, si y sólo si g - g' Î H. Al conjunto de clases de equivalencia módulo H en G (piénsese en "las posiciones relativas" que manejamos arriba), se le llama cociente de G módulo H, y se le denota G/H (leyendo, "G-módulo-H" o "G-entre-H" o G-sobre-H"); podemos escribir:
O bien,G/H={g+H,gÎG}; donde g+H={g+h; hÎH} es la clase de equivalencia de g, consiste de los equivalentes a g módulo H, y, como conjunto de G, no cambia cuando cambiamos g por cualquier equivalente; es uno de los puntos del nuevo conjunto que hemos construido, G/H, que vuelve a ser un grupo. Es interesante observar, para dejar los detalles al buen estudiante, que el cociente hereda la suma para convertirse en un nuevo grupo sólo cuando se valía en G la ley conmutativa (g + g' = g' + g), la que lo hace abeliano en vez de simple grupo, o bien cuando H es muy especial respecto a su ambiente; pues, si queremos definir la suma de dos G/H-itas, tenemos que tener claro que son clases de equivalencia, conjuntos de G, y no siempre resultan equivalentes las sumas con sumandos equivalentes. Pero, en nuestro caso, el abeliano, si p y p' son los G/H-itas que queremos sumar, sabemos que habrá por ahí un par de G-itas g y g', llamados representantes de p y p', tales que p = g + H y p' = g' + H, y la definición natural:
funciona de maravilla. Pero brinquémonos los detalles, y regresemos al caso particular que nos atañe, donde hemos conceptualizado lo suficiente para escribir sin pruritos formales:
S1 = R/Z.
Y nos atreveríamos a dejar de ejercicio el probar que la estructura de grupo
de este cociente es la de las rotaciones de un círculo rígido, aquella suma
de ángulos de la secundaria.
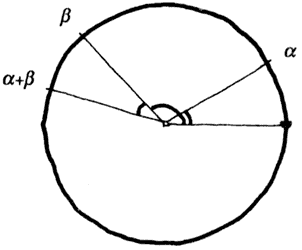
Figura 23. La suma de ángulos es el cociente de la suma de números reales.
Resumiendo, tenemos una función R ® S1 = R/Z que a cada real le asocia su clase de equivalencia. Podemos interpretarla como una función del espacio perceptivo de —o— en su verdadero universo. Las imágenes que potencialmente se podrían formar en el espacio perceptivo, suponiendo inmovilidad salvo por transparentaciones, de un mismo punto pÎS1 van a dar a ese punto bajo la función, y corresponden a un conjunto de puntos en el espacio perceptivo que entre sí distan enteros, determinándose esta clase por cualesquiera de ellos.
Definámosla de un golpe para el caso bi y el tridimensional, usando a n como comodín que remplace al 2 o al 3, pero ya entrados en gastos y viendo que también podría ser 1, y haciendo bien las analogías, hasta 0, pues que se quede como n, un natural.
Es muy fácil ver que los elementos de Rn se pueden volver a sumar y restar tal cual lo hacían cuando estaban solitos, en R, haciendo todo coordenada por coordenada. Y además, cargan con sus enteros Zn, aquéllos de puras coordenadas enteras, que se suman sólo entre ellos para formar su grupito, un subgrupo de Rn. Y habiendo pasado por las definiciones generales pertinentes, nos aventuramos a definir al toro n-dimenszonal, n-toro pa' los cuates, como:
entiendiéndolo ahora con toda la geometría que herede de Rn.
Para demostrar que coincide con nuestra anterior definición topológica, obsérvese, con el detalle que se quiera, que, de nuestras definiciones coordenada por coordenada, se tiene que Rn/Zn= (R/Z)n, pero hemos visto que S1= R/Z.
Pensemos, para fluidificar las explicaciones, que Rn se encuentra sobre el n-toro, y que la función que los une (la que a cada x Î Rn le asocia su clase de equivalencia módulo Zn, x + Zn, la que lo ve como simple posición respecto a los enteros), es el acto de "cubrirlo". Lo que entendemos por "entenderlo con toda la geometría que hereda de su espacio cubriente", para el lector que se haya sentido abrumado por la frase, es que en todas las nociones que queramos definir abajo, en el n-toro, subimos al espacio euclidiano donde las reconocemos, y las regresamos, recubriendo. Por ejemplo, si queremos soltar un estímulo luminoso abajo, pues lo soltamos arriba, dejándolo viajar por una trayectoria recta y a velocidad constante y luego veremos qué describe, qué cubre, abajo; si queremos medir esta trayectoria, pues lo hacemos antes de bajarla; así con todo lo que se nos vaya ocurriendo. Arriba, desde Euclides, ya tenemos cierta experiencia. Abajo, aunque haya costado trabajo, como que ya conocemos el caso unidimensional.
Vayamos al siguiente, n=2. Caso del que ya no pasaremos en esta sección dedicada al espacio toroidal; dejando el análogo tridimensional al lector afanoso o bien a las ensoñaciones que aún reververen desde los tiempos aquellos de la Soñata, la literaria, en su Tiempo II.
Retomemos a nuestro personaje, a WTo; a quien daremos
ahora el don de la bidimensionalidad inteligente; a quien podemos dibujar cómodamente
en esta hoja, y pensarlo en R2, con su origen perceptivo, o, el centro de su
cabecita discoidal, en el origen de R2, su cero para la suma:
o = (0, 0). Y metámoslo al toro, poco a poco, con nuestra consigna geométrica
siempre en mente. Si le hacemos un pequeño cuartito —de lados más chicos
que 1, por lo pronto— se sentirá, por consigna, tal como en la figura:
Figura 24. WTo en un cuadrito,
I x I.
Con nuestra experiencia unidimensional, podemos concluir que, manteniendo piso
y techo fijos, mientras separamos las paredes hasta desvanecerlas, WTo
tendrá el siguiente espacio perceptivo; y se podrá dar cuenta de ello con simples
cabeceos que emulen las transparentaciones de —o—.
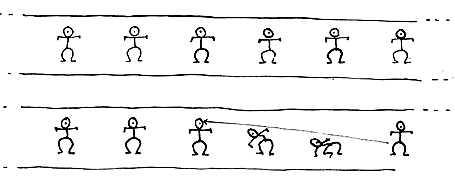
Figura 25.
Aún tenemos chance de aclarar por completo qué pasó. Sabemos que en realidad
WTo estaba, manteniéndolo entre techo y piso, en
un cilindro.
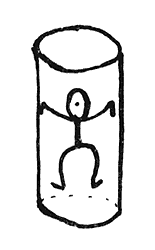
Figura 26.
Si entintamos a WTo y tomamos su "cuartito" como
rodillo que gira y que presiona su plano cubriente, el que sirvió para modelar
la geometría, obtenemos lo que horizontalmente se percibe (figura 25). A cada
vuelta del rodillo, los puntos del universito marcaron su huella sobre un representante
módulo enteros. Cualquiera de los entintados emitirá luz en la dirección de
o. Esta trayectoria se puede seguir abajo, y WTo
deberá ser lo suficientemente inteligente para esquivar con su cuerpo el paso
de este rayo antes de que sea percibido, antes de que dé tantas vueltas al cilindro
como lo requería la imagen en cuestión, el punto entintado en R2
que escogimos dentro de la pequeña franja.
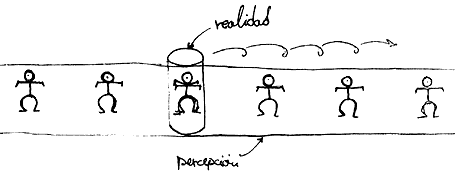
Figura 27.
Pensemos un momento que esta franja del espacio perceptivo es un universo en
sí, donde todas las imágenes son entes separados, que manejan muy bien su hacelamano-hacelatrás.
Y quitemos piso y techo. Tendremos ahora un cilindro horizontal infinito, pues
la segunda coordenada del universito es un S1 . Entintemos
de nuevo, y rodemos el rodillo por todo el piano; corolario del trabajo en dimensión
1, obtenemos el espacio perceptivo de WTo, en T2
: una imagen, WTo-n llamésmola, para cada
n Î Z2, centrada ahí, y con todos sus puntos
correspondiendo (módulo enteros) a los de WTo, el
único ser que habita este pequeño universo de volumen, área, mejor dicho en
este caso, igual a un cuadrado unitario, cuarto cómodo para WTo.
Si pensamos a WTo-o como subconjunto de R2
, centrado en el origen, entonces WTo-n será
el transladado de WTo-n por n, es decir
(WTo-n) = (WTo-o)
+ n.
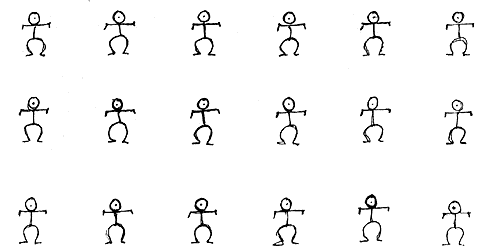
Figura 28. Percepción de WTo en el toro bidimensional.
Apaguemos la luz. Y pensemos que al momento de abrir los ojos en T2
, WTo empieza a emitir su luz cotidiana. Un instante
después, al concluir la luz su primera vuelta, aparecerán sus cuatro canchanchanes
vecinos, y antes de concluir el segundo instante, por ahí del tiempo ![]() ,
surgirán cuatro más en las esquinas, etc., etc. Después de N instantes, se podrá
ver a WTo-n siempre y cuando |n| £
N, donde |n| es la distancia al origen, medida siguiendo a Pitágoras,
por |n| =
,
surgirán cuatro más en las esquinas, etc., etc. Después de N instantes, se podrá
ver a WTo-n siempre y cuando |n| £
N, donde |n| es la distancia al origen, medida siguiendo a Pitágoras,
por |n| =![]() donde
n = (n0, n1). WTo
irá sintiendo la enormidad de R2, su espacio perceptivo.
donde
n = (n0, n1). WTo
irá sintiendo la enormidad de R2, su espacio perceptivo.
Nótese por último, antes de entrar en movimiento, que desde la sección de su topología, no hemos intentado dibujar al toro bidimensional más que en pequeños pedazos. Esto es causal.
Habiendo definido su geometría por un producto cartesiano cuyos factores corresponden a los haces paralelos "horizontal" y "vertical" en los dibujos, así como al uso dado al postulado quinto, hemos obligado a T2 a que en porciones pequeñas (que no se autodesborden) sea como esta hoja de papel; lo hemos decretado a imagen y semejanza local del plano euclidiano (de la geometría plana o euclidiana, diríamos para las demás dimensiones). De allí su apellido, el toro plano, que habíamos usado en títulos pasados; y de allí, también, que no hayamos intentado dibujarlo, pues ni siquiera en R3 = E3 cabe sin que haya que deformar, torturar hasta distorsionar, su verdadera geometría; sumergirlo en R3 sería tanto como diseñar un rodillo rígido, de superficie toroidal localmente plana —papel sin dobladuras—, que gire como birrodillo que imprime impecable sobre dos direcciones perpendiculares; T2 es una imposibilidad física del espacio tridimensional, una realidad matemática sumergible isométricamente sólo hasta R4, el espacio plano tetradimensional. Como ejemplo indicativo de la veracidad de este teorema, que no demostramos, nótese que en la figura 16, que representa a un toro en R3, los círculos de uno de los factores (el horizontal) cambian cíclicamente de tamaño, algo que nunca sucedería en nuestro toro plano; o bien, obsérvese que al cubrirlo con papel maché habrá que usar pedacitos y mucho engrudo para flexibilizarlos; no es localmente isométrico a un plano.
Hemos rendido cuentas de la panorámica general que nuestro joven personaje de la agorafobia en el Tiempo II percibe al estar solo en el toro plano. Para concluir nuestros apuntes sobre/en este espacio, comentamos, breve e intuitivamente, la fundamentación matemática de dos escenitas que ocurrieron ahí; dejando el efecto sonoro —canta WTo el tema de La Novena de Beethoven, se escucha, y trata de hacer música, ¿qué sucede?— al trabajo de ejercitación y entendimiento del lector estudioso, y manteniéndose, para las figuras y el pensamiento geométrico —como ya habíamos establecido—, en el caso bidimensional.
El problema que nos planteamos aquí es ¿qué ve WTo al moverse en T2?
Para responder en forma precisa, habría que describir en forma precisa su movimiento:
Podemos pensar que T2 está fijo y que WTo se desplaza en él. Pensemos a WTo como un simple conjunto de puntos, W, cohesionados entre sí de alguna manera, biológica quizá, para mencionar, aunque sea de paso, un término mágico. Y tenemos que para cada tiempo t, WTo ocupa un determinado lugar en su universo. Entonces, el movimiento estará determinado por una función
donde el factor R parametriza al tiempo. Así, si z Î W (que representa, por decir algo, la punta de un zapato), f (z, t) es la posición de z en el tiempo t.
Lo que WTo verá en un tiempo determinado t0
está dictado por el tiempo pasado. De hecho, como ya habíamos acordado desde
las "Notas generales", recibirá un estímulo e = (p, d, t) asociado a
algún punto z Î W, si y sólo si: i) p =
f (z, t), es decir, z estuvo en p en el tiempo t (para
lanzar su estímulo), y ii) saliendo de p en la dirección d a velocidad-luz
y sin volante —como rayo de luz— llegamos en un tiempo t0
- t a f (o, t0), es decir, origen perceptivo
y estímulo luminoso se dan cita a las t0 en el punto p0
= f (o, t0), y llegan justos.
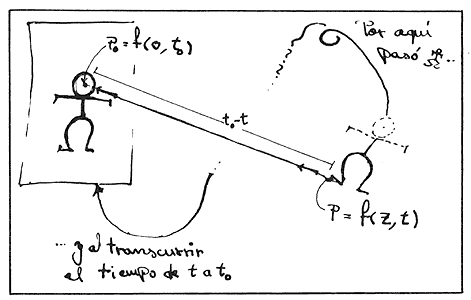
Figura 29. Foto en tiempo t0.
Nos ahorramos el exigir que el viaje de e no haya sido obstruido por WTo en su recorrido incógnito —dictado por f—, pues hemos aprendido ya de las transparentaciones.
Veamos un ejemplo sencillo. En T2, pues, cabe subrayar que
lo que llevamos de sección y algo de lo que sigue es generalizable a otros universos,
aunque lo mantengamos en silencio para no pecar de abstractos y salir rápido
del trance. En T2, decíamos, y con el movimiento más simple
de todos: el inercial a velocidad constante v, no cero y menor a la de la luz,
es decir 0 <v < 1, pues recordemos que la velocidad-luz ha quedado
determinada por el 1 en nuestra parametrización de T2. WTo
viaja, sin esforzarse, en movimiento rectilíneo uniforme; y, para simplificarlo
aún más, supongamos que es "hacia arriba" la dirección positiva del segundo
factor de nuestro toro (siendo v más-menos a medio cuerpo por instante
en los dibujos que siguen, aunque el texto proceda en general para cualquier
v entre 0 y 1, dejándole rebasar esta cota superior al lector). En este
caso, la función de movimiento es sencilla, a saber f ((x0,
x1), t) = (x0, x1
+ tv), donde z Î W se identifica con su posición
(x0,x1) en el tiempo 0.
Figura 30.
Revivamos pues a WTo, quien, tras parametrizar su espacio perceptivo en relación nítida con su universo, regresa de un sueño bien merecido. Abrámosle los ojos en el tiempo t0 para que tome una foto de lo que percibe en el instante justo t0 = 0. Y supongamos que viene moviéndose como indicamos arriba desde siempre, es decir, con todo el tiempo que requiera para estudiar su situación.
Sabiendo que estamos en T2, instintivamente buscamos a WTo-1
(donde 1 = (1,0) Î Z2), nuestra
imagen vecina.
Figura 31.
A distancia uno no hay nadie. Pues hace un instante estábamos en (0, - v)
(1, - v), y en (1, 0) = 1 ~ o no había nadie; a menos que WTo
sea cabezón respecto a la velocidad. Notemos, inclusive, que la luz que salió
de o Î W en t = - 1 con la dirección
de la figura, todavía no llega a (0, 0) en el tiempo t0; la
distancia de (1, - v) a (0, 0) es mayor que 1.
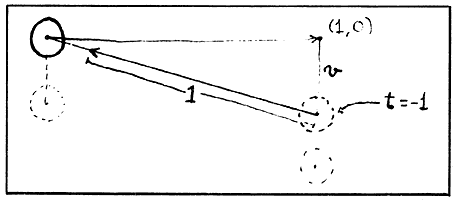
Figura 32.
Para encontrar a WTo-l, nuestro fiel compañero de
andanzas que debe andar por ahí, tenemos que retroceder más en el tiempo, y
por ende, bajar en su línea vertical, equivalente a la de nuestro movimiento
perceptual. Su centro deberá llegar al punto 1(~o) en un tiempo igual a su distancia
al origen. Es decir, hay que resolver la ecuación.
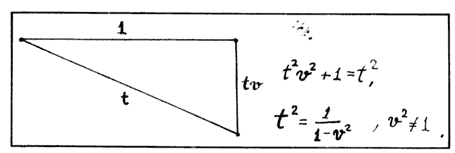
Figura 33.
Sea entonces t1 la solución negativa a esta ecuación, que
existe por hipótesis. El estímulo luminoso que sale del origen de WTo
en la dirección de (1, t1 v) a (0, 0), es percibido
en el tiempo t0 ; "autopase completo de WTo
a WTo".
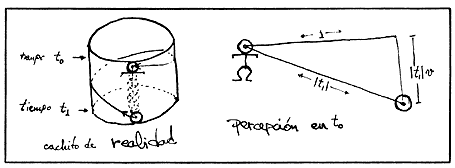
Figura 34.
Y ya que descubrimos el centro de WTo-l, busquemos
sus zapatos, o bien, un punto z bajo su centro, para ser más precisos.
Fijémonos en z en el tiempo t1 ; el rayo que emite
hacia o no llegará a tiempo a su cita para ser percibido en t0
.
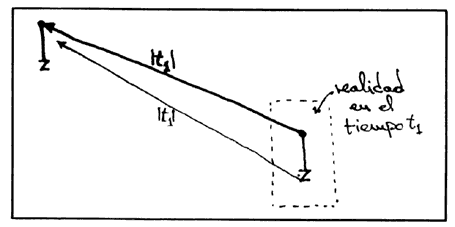
Figura 35.
Sin embargo, nuestra intuición nos dice que debe haber un z-equivalente
rondando a un o-equivalente; un zapato se conecta por un cuerpo a su
cabeza. En efecto, pero debemos buscar al z de WTo-l
más en el pasado; y notando que z viaja rígidamente pegado a o
y por la mismita vía, obtenemos la siguiente figura, "foto en t0".
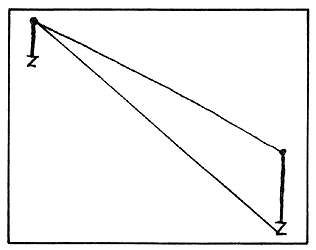
Figura 36.
Nuestra imagen vecina (lateral a nuestro movimiento), WTo-l, se ha retrasado y alargado.
¿Puede el lector dar las coordenadas precisas de z Î WTo-l (figura 36)?
¿Puede explicar por qué la imagen que viene persiguiendo WTo
se verá más cerca y achaparrada?
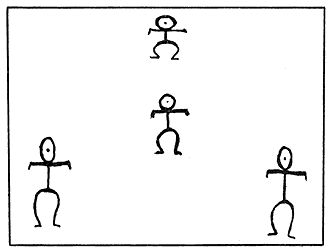
Figura 37.
¿Se aventura a añadir imágenes a la figura anterior?
¿Puede imaginar qué pasa si WTo empieza a maniobrar, cambiando la dirección de su vuelo?, ¿si empieza a acelerar, se acerca, juega con, y rebasa la velocidad de la luz?
¿Puede demostrar que un punto x + Z2 Î T2 presenta como imágenes en el espacio perceptivo en el tiempo t0 = 0, al siguiente conjunto
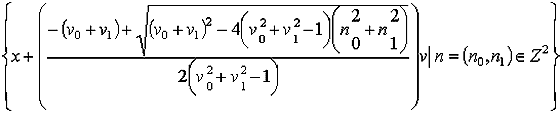
donde v = (v0, v1) es el vector velocidad del movimiento rectilíneo uniforme en que viaja WTo desde tiempo infinito?
¿Puede usar esta fórmula para hacer que una computadora dibuje espacios perceptivos de T2, bajo distintas y variables condiciones de movimiento —inercial, para empezar?
Deformación de la geometría (topología)
Es claro que si WTo (viviendo en T2) lanza un mecate por su lado derecho lo recibirá con su mano izquierda. ¿Qué pasa si buscando aproximarse a sus imágenes jala con fuerza de ambos lados?
La física de nuestros universitos no ha sido definida con la precisión suficiente como para deducir una respuesta. Podemos, sin embargo, tomar dos caminos: decretarlos rígidos, de tal manera que la geometría permanece inalterada, siendo entonces infructuoso el jaloneo —y esta sección— o bien, suponer que la energía —concentrada universalmente en los músculos de WTo— es capaz de modificar la estructura geométrica.
Para la Soñata (en el pasaje que enlaza los dos subtiempos del Tiempo II, cuando nuestro joven personaje, huyendo de la agorafobia, cayó jalándose a sí mismo en la claustrofobia, acabando a punto de orinarse ante la tortura, o bien, de perecer por asfixia) tomamos la segunda ruta, guiados por la intuición topológica. Me ciño al son de la Soñata.
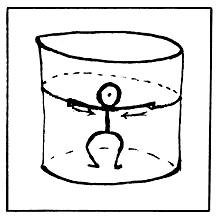
Al jalar WTo de una geodésica cerrada, de una curva
de longitud mínima entre sus vecinas, la dejamos ceder, es decir, permitimos
que se acerquen sus manos reduciendo un poco el largo de su cuerpo.
|
|
|
Figura 38. |
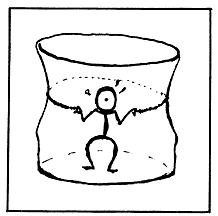
Figura 39. |
La geometría cambia; la topología permanece. Se acortó una curva, una cuerda
tensa por la resistencia del universo, pero a la topología las distancias la
tienen sin cuidado. En el justo momento del jalón, suponemos que el toro con
el cinturón apretándose se vería en foto instantánea y con la geometría de vivir
en R3, como algo así:
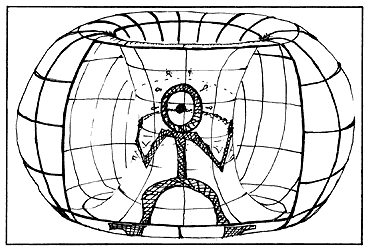
Figura 40.
Pero si dejamos las cosas tal cual vagamente están, perderíamos la planaridad del toro, su definición precisa, y toda la herramienta que con tanta paciencia hemos construido.
Suponemos entonces —aunque me gustaría invocar alguna ley pomposa, es simple
hipótesis de trabajo— que este universito tiende a aplanarse; que busca
homogeneizarse y después de unas vibraciones (que no me atrevo a definir) por
su espacio continuo de geometrías, regresa a un estado de planaridad local,
ganando WTo un poquito de terreno. Es fácil precisarlo:
reducimos el tamaño de un factor S1, el que se apretó.
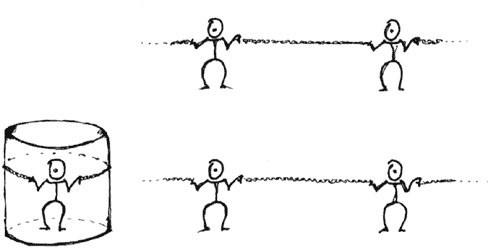
Figura 41.
(Anoto que) WTo no tuvo tiempo de montar en su aparato
descriptivo de la realidad perceptivo-visual qué aconteció al irse incorporando
al pasado este simple fenómeno de propinarle un jalón que le duela y afecte
a su universo (para que quede como ejercicio avanzado), pues se fijó más bien
en el "dolorcito" aquel que sintió en el pecho y que significaba la deformación
local de la geometría, la salida momentánea y tensa de la planaridad punto a
punto. Pero regresó a ella y siguió jalando, aprendiendo a sentir (disfrutar)
los "escalofríos eléctricos", hasta agarrarse de sus manos extendidas y abrazarse
gustoso a sí mismo. Sin dificultad, encaramándose ahora sobre los tocados, hizo
lo mismo con la dirección perpendicular, reduciendo el otro factor.
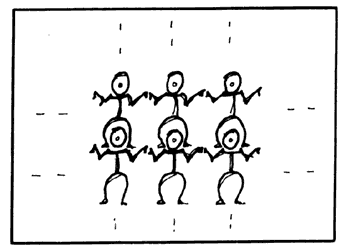
Figura 42.
Puede ahora tomar su pie izquierdo, extendiendo hacia arriba su mano derecha y jalar fuerte con sendos miembros.
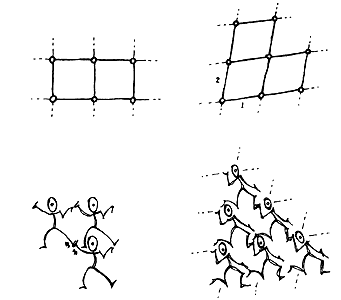
Figura 43.
Ha cambiado la geometría, y quizás el área se haya resentido un poquito; pero, guiados por la intuición de la reja que se reclina sobre un eje, o por el último dibujo, podemos definirle su geometría al nuevo toro: es el cociente de R2 módulo el subgrupo de combinaciones (posibles sumas) enteras de 1 y 2 (véase la figura). Podríamos pensar en una reparametrización a la Descartes, en que sólo hemos cambiado las varas de medir, puesto que la suma de R2 coincide con tomar distancias dirigidas de un origen fijo en el plano euclidiano, para luego usarlas como pasos de un mapa del tesoro. Tenemos que, dados dos tipos de pasos dirigidos, no colineales, retornos permitidos, podremos llegar saltando a unas islitas parametrizadas por Z2 (parejas de números): "cuántos brincos de uno y cuántos del otro tipo". El nuevo toro consiste entonces en las posiciones relativas a nuestros puntos-islotes, con la geometría heredada por el plano euclidiano que lo cubre; las varas de medir en este nuevo universo se han "descuadrado" (abandonado la perpendicularidad) y se han acortado respecto a su único habitante.
En este proceso de jaloneo (que terminó, al avanzar la agorafobia, en patadas y empujones desesperados) nos hemos movido por las geometrías del toro. Y ahora estamos hablando del toro topológico: el que se mantuvo inamovible ante las deformaciones; el que siempre siguió dando su forma básica, su cohesión puntual al universo, sin importarle distancias, áreas, volúmenes o ángulos. (El que, con alguna de sus geometrías y en la dimensión adecuada, podría ser el nuestro.)
Notemos además que le estamos dando al toro geometrías planas, es decir, que fuera de perturbaciones despreciables el espacio sigue siendo localmente euclidiano, justo como éste que ocupa nuestro cuerpo. Podemos entonces reducir el volumen del universo hasta hacerlo casi coincidir con el de su único habitante, dejando apenas un poquito de aire bordeando las pequeñas áreas de piel que no están presionadas por otras partes de la misma piel, sin necesidad de especular sobre el comportamiento fisiológico —de los huesos, por ejemplo— ante geometrías que localmente no son planas, ante curvaturas extrañas a la de nuestra experiencia cotidiana. Supusimos, por cierto, que para reexpander su universo se requería algo más que la fuerza bruta, haciéndoselo imposible a nuestro cautivo personaje; de ahí que empujar se traducía en presión desde otras direcciones, y que irremediablemente se fuera reduciendo su universo hasta casi coincidir con su cuerpo. No nos atrevimos a llegar al límite. Sin embargo, Escher, con hermosas parejas de seres bidimensionales, sí lo ha logrado.

Figura 44
La caverna en que se refugió nuestro atormentado personaje claustrofóbico, el escenario donde transcurre el Tiempo II en su parte segunda y última, la que se hizo caverna-tenis para finalizar en la agujeta-caverna-brócoli, es la hermana tridimensional de la distinguida familia de las esferas:
La n-esfera, Sn, consta de los puntos a distancia uno del origen, de los "vectores" de magnitud unitaria, en Rn+1; podemos entonces explicitar
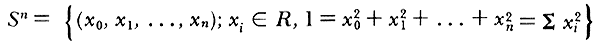
y dibujar los tres primeros casos:
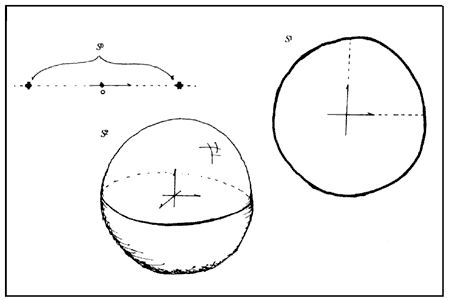
Figura 45. Las esferas de dimensión 0, 1 y 2.
Las esferas obtienen su geometría al vivir, por decreto definitorio, dentro de un espacio euclidiano: el de dimensión siguiente.
Es fácil ver que las geodésicas, las trayectorias mínimas que unen los puntos,
corren a lo largo de círculos máximos. Nótese, para husmear el ¿por qué?, que
entre más grande es un círculo en esta hoja, más se parece a una recta. Así
que para irse de un punto p0 con prisa de llegar a p1
, en el entendido de no salirse de esa esfera "cascarita", lo mejor será agarrar
por su intersección con el plano que pasa por el origen, p0
y p1 . Esta intersección es un círculo máximo; un S1 tal cual
se acaba de definir (los puntos a distancia unitaria del origen en un plano
euclidiano); sobre ese S1, viajará la luz de p0
a p1 .
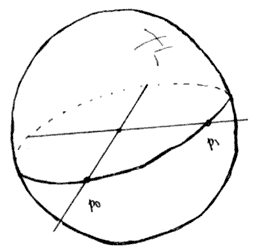
Figura 46. La geodésica de p0 a p1
en S2.
Obsérvese —de los mismísimos axiomas de Euclides, si se quiere— que
el plano que acabamos de utilizar es único, salvo en el caso en que o,
p0 y p1 sean colineales; y en este caso
especial decimos que p0 y p1 , son antípodas,
forman un S0, su relación es distinguida, y cada punto en
la esfera distingue a su antípoda de todos los puntos de su universo, pues vienen
en parejas.
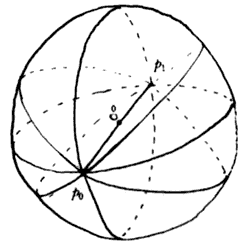
Figura 47. Par de antípodas.
Un punto en la esfera comparte a todas sus geodésicas con su punto antípoda, es su Roma para los caminos de luz que de él emanan, su inverso para la suma, obtenido al cambiar los signos de todas sus coordenadas, o bien, multiplicando por -1.
Se explica entonces la escenografía.
Se mueve un origen perceptivo ó en la esfera. Si su antípoda -o, que se mueve conforme a o aunque esté muy lejos, de hecho, lo más lejos posible para este universito —dos, tres metros en la Soñata—, está transparente, es decir, si -o no afecta en nada a los rayos de luz que pasan por él, entonces este ser perceptivo se verá a sí mismo invertido (en cada dirección ve el punto en que abandona su cuerpo el rayo que pasa por o en la dirección dada). Se sentirá en la caverna.
Pero en el momento en que ese punto antípoda al origen perceptivo, el "anticentro", se hace opaco, se recubre, digamos, de algún objeto material, verbigracia, un tenis, las cosas habrán cambiado drásticamente. Todos los rayos de atención que salgan de nuestro centro o, viajando por geodésicas hacia el pasado, chocarán con el objeto que cubre al anticentro -o. Lo veremos entonces en todas direcciones, interpretando, con nuestro mecanismo de visión tridimensional, a cada punto de su superficie visible como puesto a una distancia aproximada a la mitad de la circunferencia del universo; llamémosle instante-luz; p radios o la distancia entre antípodas. En el espacio perceptivo (el euclidiano de la misma dimensión que la esfera-universo y que debemos identificar con el tangente a ella en o) veremos, desde su justo centro, toda una esfera —la hermanita menor del universo con el radio citado— de estímulos luminosos rodeándonos, pero en la realidad, esos estímulos que forman una pantalla-caverna salieron todos del mismo punto, el antípoda, hace exactamente un instante, y vienen empapados con la información —el color, el tiempo— del punto por donde emergieron de la opacidad. Basta que el anticentro se cubra, se opaque con un granito de arena, para que aparezca una caverna intermedia esbozando luminosamente a una hermanita menor, mostrándonos la superficie de aquel polvo alejado al máximo de nosotros.
Dejamos al lector que se explique solito los efectos visuales de los amaneceres
del anticentro, o de su introducción pausada y cuidadosa a una región opaca
del espacio. Quizás ayude el siguiente boceto coreográfico para el movimiento
escénico del punto antípoda al origen perceptivo en la escena de exploración
del tenis.
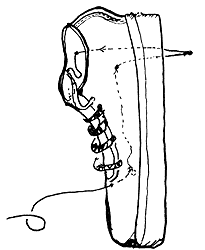
Figura 48. Viaje del anticentro de acuerdo al tiempo
II.ii.
ACCIÓN DE LA HERMANITA MENOR CON REINTEGRO
S0, la hermanita menor de nuestra familia, la cero-esfera, es el conjunto {1, -1 } de números reales que, con el producto, forma un grupo, el más chico no trivial: al multiplicar por uno nada pasa, y al multiplicar por menos-uno se permutan (se comportan, pues, como pares e impares sumándose en los enteros. Por eso a este grupo se le conoce también como los enteros modulo 2).
Ya que cualquiera de sus hermanas mayores admite a su vez ser multiplicada por S0 (por el uno fijándola y por el menos uno permutando antípodas), tenemos una acción de S0 en Sn y podemos pensar en su cociente, Sn/S0: espacio continuo y métrico de órbitas (parejas de antípodos en nuestro caso). Podemos pensar así en estas órbitas como puntos, e identificarlas (cada órbita entre sí) para formar un nuevo espacio de "posiciones relativas" a una órbita dada, el cociente bajo la acción.
Recordemos que al discutir nuestra visión en el espacio proyectivo descubrimos un plano al infinito de un punto o, que llamamos ¥ (o); vimos también que cada punto en él se percibía al mismo tiempo-distancia en direcciones opuestas, es decir, los puntos del plano proyectivo ¥(o), tal como los de cualquier otro, corresponden a las líneas por o, o bien, a las parejas antípodas en una dos-esfera perceptiva. Generalizando, definimos entonces al n-espacio proyectivo como:
Podríamos invitar al lector interesado a repasar, con esta definición en mente, la sección dedicada al espacio proyectivo, demostrando todo a su paso, empezando por los axiomas. Sin embargo, tendrá que aventurarse él solo, pues en este punto el libreto nos obliga a concluir en un dodecaedro:
Considérese un pentágono (plano y regular por definición), pensándolo como lo acotado por cinco líneas cuyas intersecciones por parejas contiguas en un orden cíclico —llamadas vértices— limitan, en sus líneas respectivas, segmentos iguales —lados— que se encuentran en ángulos iguales, o bien, que distan lo mismo de un mismo punto —su centro.
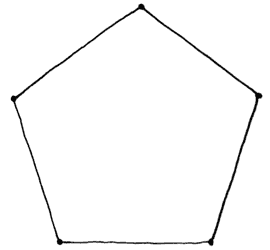
Figura 49. Pentágono equilátero.
Este pentágono euclidiano, independientemente del tamaño de sus lados, tiene los ángulos fijos, entre 90° y 120° (tres pentágonos no ajustan pero cuatro sobran para una vuelta).
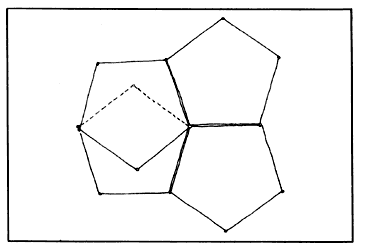
Figura 50. Para una vuelta, cuatro pentágonos sobran y tres no alcanzan.
Y será esencialmente el mismo si lo metemos a vivir en una esfera inmensa (sus
medidas no cambian aunque recordemos que la Tierra es redonda); pero cambiará
su geometría conforme sus dimensiones se aproximen a las de su universo. Fijemos,
para ver esto, un origen o en S2 Si lanzamos desde
o cinco estímulos regularmente distribuidos, y pensamos en los segmentos
geodésicos, que cíclicamente los unen en todo momento, tendremos, con centro
fijo, a una familia creciente de pentágonos esféricos regulares. Cuando los
cinco vértices emisarios lleguen al ecuador ortogonal del centro de partida,
los cinco lados se ajustarán para formar una sola geodésica (¿qué sucede con
este experimento en P2 ?); el ángulo del pentágono ha llegado
a 180°, y éste se ha convertido en la cascarita de una media naranja, perdiendo
los "picos".
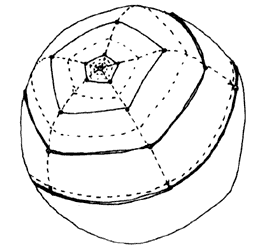
Figura 51. El ángulo de los pentágonos esféricos varía conforme al radio.
Podemos concluir que en algún punto de su viaje los emisarios forman un pentágono regular cuyos ángulos miden 120° tres de éstos se acomodan justos por sus esquinas:
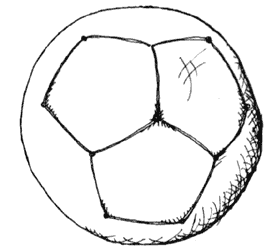
Figura 52. Pentágonos esféricos con ángulo de 120—.
En los nuevos huecos van embonando otros de estos pentágonos, y otros más.
Con doce de ellos se ha cubierto por completo a la esfera, que queda enmosaicada
con pentágonos iguales, dispuestos con la estructura del dodecaedro (esférico,
especifiquemos). Los vértices de cada mosaico están en un plano euclidiano (como
lo estarían los de cualquier pentágono o polígono esférico regular; al espacio
que queda acotado por estos doce planos en R3 , se le conoce,
desde los griegos y asociado al nombre de Platón, como dodecaedro (que
aquí apellidaremos euclidiano). Este sólido queda inscrito en la esfera
original y comparte con ella sólo sus veinte vértices.
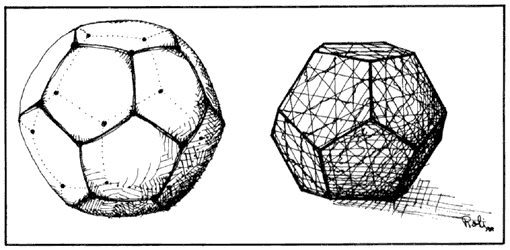
Figura 53. Dodecaedro esférico y dodecaedro euclidiano (uno de los
sólidos platónicos).
—...Finaliza el intermedio; regresa cuchicheante el público a sus lugares; y, para variar, nos ha ganado el tiempo. Sólo nos queda entonces, amigos televidentes, pedirle al escenógrafo que tan gentilmente nos ha acompañado en la cabina, un apunte brevísimo sobre el escenario del último acto de la Soñata que estamos a punto de reiniciar para conluir, en su estreno mundial que transmitimos hoy, en vivo y a todo color, por XFCE. ¿Tiene algo rápido con qué concluir, señor escenógrafo?
—Bueno. A ver... Recojamos nuestro tinglado. En la Soñata nos habíamos quedado dentro de la tres-esfera, S3 , la caverna-tenis-agujeta: reingresemos a ella. Y estábamos a punto, en los Apuntes, de considerar al dodecaedro esférico, figura 53, como dibujado en el plano, dos-esfera máxima, S2, ecuador de distancias entre nuestro origen perceptivo y su anticentro o antípoda (recuerden, estamos en S3).
Mandemos llamar a nuestros veinte emisarios (vértices del dodecaedro ecuatorial) jalándolos por sus hilos-luz a nuestro origen. Notemos que un instante imperceptible, un infinitesimal antes de llegar, forman un dodecaedro euclidiano indiferenciable de estos de ónix que tengo en mis manos. Observen ustedes cómo puedo juntar a tres de ellos por una arista, sobrando algo de espacio para el ajuste impecable; conclúyase, pues, que en algún momento pasamos por un dodecaedro esférico de empaque ideal: caras encontrándose en ángulos de 120 grados. Quedémonos en el interior sólido en S3 de este dodecaedro esférico específico, ajustando su volumen al de este cuarto inflando a toda la esfera. Y ahora, deshagámonos de su frontera: identifíquense piso y techo pentagonales tirando de ellos hacia el centro y empalmándolos isométricamente al llegar a él por el giro de mínimo esfuerzo, anulándoles así su condición de frontera. Procédase asimismo con las cinco parejas restantes de caras opuestas. Se han borrado los límites. Estamos ya en el espacio dodecaédrico, también conocido como la variedad de Poincaré, definible como el espacio fase de dodecaedros inscritos en una esfera euclidiana fija, o como cociente de ciertos hermosos grupos, o por medio de cirugía en el nudo trébol, o de algunas otras maneras muy bien documentadas en la cuarta sección de mis apuntes. Sin embargo, lo importante no es que...
—Discúlpenos, señor escenógrafo, pero nos piden ya silencio absoluto, concrete rápido.
—Bueno, agradecer la atención del público... de nuestros patrocinadores... y que en el mundo matemático actual, lo que no sabemos es lo que dice el Mago que...
—Muchas gracias por su presencia en esta cabina, señor escenógrafo. Y ahora, de acuerdo con el programa, retornemos a la Soñata.