VIII. MATERIALES MAGNÉTICOS

EN ALGUNOS materiales, a los que llamaremos materiales magn�ticos, se observa que sus �tomos o iones se comportan como si fuesen peque�os imanes que interact�an entre s�.²⁴ En estos casos se dice que los �tomos tienen un momento magn�tico diferente de cero, el cual se caracteriza por su magnitud y la direcci�n en la que est� orientado. En lo sucesivo, a estos peque�os imanes los denominaremos espines magn�ticos o simplemente espines.

Pero no todos estos materiales se comportan de la misma manera, debido a que sus propiedades magn�ticas dependen de dos factores. �stos son: la magnitud de sus espines individuales, y la orientaci�n relativa de �stos: Si los espines no tuviesen ninguna interacci�n, ya sea entre ellos o con sus alrededores, entonces cada uno de ellos podr�a apuntar en cualquier direcci�n, puesto que no tendr�a preferencia alguna. Sin embargo, �ste no es en general el caso: la orientaci�n que tomar� cada uno de ellos depender� del balance de varios factores que pueden resumirse en factores internos y externos.

Como su nombre lo indica, los factores internos dependen de las caracter�sticas intr�nsecas de cada material, esto es, del tipo de interacciones entre los espines. Por otro lado, los factores externos son los que est�n relacionados con el ambiente, es decir, que dependen de la interacci�n del sistema con sus alrededores. Como ejemplo de factores externos tenemos la posible existencia de un campo magn�tico producido por una fuente ajena al material, y por otro lado, de manera muy importante, la temperatura ambiental, ya que el medio ambiente funciona como una fuente de calor y agitaci�n para el material.

Un ejemplo t�pico de un material magn�tico, que todos conocemos, es el de los imanes permanentes. En este caso, una gran parte de los espines est� alineada permanentemente en la misma direcci�n relativa. Y aunque el campo producido por cada uno estos espines es muy peque�o, al sumarse sus contribuciones individuales se produce un campo magn�tico que puede observarse macrosc�picamente.

En el otro extremo tenemos los materiales paramagn�ticos. En estos materiales los espines apuntan en direcciones totalmente azarosas, por lo que las contribuciones de los espines individuales tienden a anularse. Como consecuencia, a nivel macrosc�pico no se observa un campo magn�tico resultante. Sin embargo, existen localmente peque�os campos magn�ticos producidos por los espines, y un peque�o "im�n de prueba" sentir� las variaciones de este campo a lo largo del material.

INTERACCIONES ENTRE LOS ESPINES

Las interacciones entre los espines son originadas por mecanismos diversos, algunos de los cuales no son del todo conocidos. Sin embargo, para nuestra discusi�n, �nicamente es pertinente conocer el efecto de dichas interacciones, sin importar las causas que las originan. Lo que s� es necesario se�alar es que debido a un principio muy general de la naturaleza, la orientaci�n final de los espines ser� aquella en donde la energ�a libre del sistema sea m�nima. Para explicar a qu� nos referimos, haremos una analog�a entre un par de espines microsc�picos y dos imanes permanentes. Esta analog�a nos permitir� hacernos una idea acerca de lo que sucede a nivel molecular.

Si tomamos dos imanes permanentes, observaremos que los extremos de uno y otro se atraen o se repelen, debido a que cada uno de ellos tiene dos tipos de polos magn�ticos. Como consecuencia, si los ponemos en contacto veremos que tienden a alinearse de una cierta manera que resulta "natural" para ellos. Decimos entonces que los imanes han tomado su posici�n de m�nima energ�a, o de equilibrio. Si ahora tratamos de girar uno de ellos 180°, veremos que necesitamos hacer un trabajo; esto es, dado que esta nueva posici�n es de energ�a mayor que la anterior, necesitaremos suministrar energ�a para lograr y mantener esta nueva posici�n, ya que en el momento en que dejemos de administrar esta energ�a extra, o sea, en cuanto dejemos de hacer fuerza para detener a los imanes y les permitamos girar libremente, �stos cambiar�n de direcci�n y se alinear�n de nueva cuenta en su antigua direcci�n, esto es, regresar�n a su estado de m�nima energ�a.

Algo similar sucede a nivel microsc�pico con los materiales a que nos hemos referido, �nicamente que en vez de tener un par de imanes, tendremos un n�mero del orden de 10²³ peque�os imanes interactuando entre s�. Entonces, cada par de espines tratar� localmente de orientarse de la forma m�s natural posible, es decir, de manera que la energ�a de ese par sea m�nima. Como resultado de este proceso tenemos una gran diversidad de comportamientos en los diferentes materiales magn�ticos.²⁵

PROPIEDADES DE LOS

MATERIALES MAGN�TICOS

Los materiales se clasifican de la siguiente manera de acuerdo con sus propiedades magn�ticas (v�ase la figura 42):

1) Diamagn�ticos. Son aquellos materiales en los que sus �tomos no tienen momento magn�tico resultante; debido a esto no pueden interactuar magn�ticamente con otros materiales.

2) Paramagn�ticos. Son materiales en los cuales los �tomos s� tienen momento magn�tico. Sin embargo, en ausencia de un campo magn�tico externo los espines individuales apuntan en direcciones diversas, de manera que sus contribuciones individuales se anulan; como consecuencia, no se observa un campo magn�tico resultante. Si se aplica un campo externo, entonces los espines se orientan ligeramente, dando como resultado una imantaci�n en la direcci�n del campo aplicado. Todos los materiales magn�ticos se comportan como paramagnetos cuando se encuentran a una temperatura alta;²⁶ se dice entonces que se encuentran en su fase paramagn�tica. Este comportamiento se debe a que a temperaturas altas los factores externos dominan sobre los internos, por lo cual el tipo de interacciones entre los espines pierde importancia.

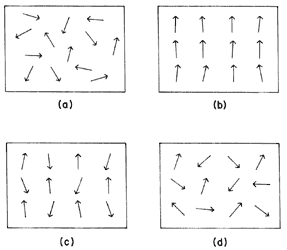
Figura 42. Diferentes tipos de materiales m�gneticos. a) Paramagneto. Los espines apuntan en direcci�nes al azar, las cuales var�an al paso del tiempo. b) Ferromagnetos. Los espines tienen tendencia a alinearse en una misma direcci�n. c) antiferromagnetos. Tendencia de los espines a alinearse antiparalelamente a sus vecinos. d) Vidrios de esp�n. Los espines apuntan en direcciones aparentemente al azar, pero fijas al paso del tiempo. Para poder diferenciar entre los casos a) y b) necesitamos observar ambos sistemas durante un largo tiempo.

3) Ferromagn�ticos. En estos materiales las interacciones entre los espines son tales, que �stos tienden a alinearse paralelamente. Debido a esto, a temperaturas bajas, esto es, cuando los efectos internos son mucho m�s importantes que los externos, hay en estos materiales una orientaci�n �nica con la cual se reduce a su valor m�nimo la energ�a del material. Esta orientaci�n corresponde a todos los espines que apuntan exactamente en la misma direcci�n.

4) Antiferromagn�ticos. En estos materiales, las interacciones entre los espines tienden a alinearlos antiparalelamente. Como resultado, a bajas temperaturas y en ausencia de un campo magn�tico externo, habr� una configuraci�n �nica de m�nima energ�a. En este estado del sistema, todos los espines apuntan alternadamente hacia arriba y hacia abajo, y el material no exhibe magnetismo a nivel macrosc�pico.

5) Vidrios de esp�n. En este tipo de materiales encontramos que algunos pares de espines van a reducir su energ�a si se alinean paralelamente, mientras que otros lo van a hacer cuando sus posiciones sean antiparalelas. Dado que cada esp�n interact�a con muchos otros espines, algunos de "sus compa�eros" le pueden "pedir" que se alinee en una direcci�n y otros en otra. Una consecuencia ser� que no todos los espines se puedan poner de acuerdo y que a temperaturas bajas no habr� una, sino muchas configuraciones diferentes que correspondan a estados de energ�a m�nima. Para cada una de estas configuraciones tenemos que no todos los pares de espines contribuyen a reducir la energ�a libre; entonces se dice que los pares que no contribuyen se encuentran frustrados. Por consiguiente toda configuraci�n de m�nima energ�a contendr� muchos pares frustrados, diferentes en cada caso, ya que no ser� posible hacer que todos ellos contribuyan simult�neamente a reducir la energ�a del sistema.

Durante la d�cada pasada y principios de ésta, los vidrios de esp�n atrajeron el inter�s de muchos cient�ficos debido a que presentan propiedades para las cuales no se encontraba explicaci�n.²⁷ Actualmente se entiende bastante bien su comportamiento, y se sabe que la frustraci�n desempe�a un papel central en �ste. Todo el trabajo de investigaci�n realizado en este campo nos ha permitido entender otros problemas an�logos, que tienen en com�n la presencia de frustraci�n; �stos son los problemas complejos.

Los vidrios esp�n ser�n el foco de nuestra atenci�n debido a la propiedad de que su energ�a libre posee muchos m�nimos. Por tanto, m�s adelante volveremos a tocar este tema para explicar con mayor detalle sus propiedades.

MODELO MATEM�TICO DE LOS SISTEMAS MAGN�TICOS

Para poder predecir las propiedades de los materiales magn�ticos es necesario, primero, hacer un modelo o idealizaci�n que describa dichos materiales de una manera simple pero sin dejar de lado las caracter�sticas esenciales del sistema, y segundo, hacer los c�lculos pertinentes para ese modelo dentro del marco de la mec�nica estad�stica. Una vez que se han seguido estos dos puntos, se confrontan los resultados de los c�lculos matem�ticos con los resultados obtenidos experimentalmente. Esta comparaci�n nos permitir� evaluar si el modelo logr� captar las caracter�sticas fundamentales del sistema a estudiar, y nos aportar� nuevos elementos que permitir�n confirmar, modificar o desechar el modelo.

Existen varios modelos para describir los materiales magn�ticos. Nosotros utilizaremos el llamado modelo de Ising, seg�n el cual los espines pueden orientarse �nicamente a lo largo de dos direcciones: hacia arriba o hacia abajo. Para explicar la idea de este modelo, dividiremos mentalmente el material que queremos describir en bloques peque�os, de manera que en cada bloque se encuentre localizado un esp�n. Matem�ticamente, denotaremos al esp�n que se encuentra en el lugar i-�simo por medio de la cantidad S_i, la cual podr� tornar dos valores: +1 si el esp�n apunta hacia arriba, y -1 si apunta hacia abajo. Llamaremos configuraci�n a cada uno de los posibles arreglos o combinaciones de estados de los espines (v�ase la figura 43).

La funci�n que representa la energ�a total del sistema se denomina hamiltoniana y est� dada por la ecuaci�n:

H= - S J ij S i S j - h S S i ,
( ij )	i	(1)

en donde j es otro �ndice mudo, esto es, toma (de uno por uno) todos los valores entre 1 y N; Jij representa la magnitud de la interacci�n existente entre los espines i y j. Por otro lado, el s�mbolo S , presente en el primero y segundo t�rminos de la ecuaci�n (1), significa que debemos sumar, sobre todos los pares de espines y sobre todos los espines respectivamente.

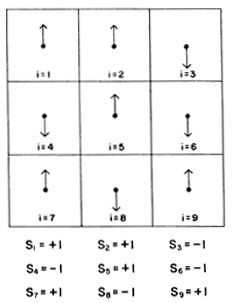
Figura 43. Este diagrama ilustra lo que ser�a el modelo de Ising para una peque�a muestra hipot�tica del material magn�tico. El valor de i indica el n�mero de cuadro dentro del material, y el valor de S₁ nos dice la orientaci�n que tiene el esp�n localizado en dicho lugar.

La ecuaci�n que acabamos de escribir nos dice lo siguiente: la energ�a total del material est� dada por la suma de las energ�as de interacci�n de cada uno de los pares de espines (i, j), m�s la energ�a de acoplamiento del sistema con el campo magn�tico externo h. Es decir, si conocemos el valor de las interacciones {Jij}, el uso de esta ecuaci�n nos permitir� calcular la energ�a total que corresponde a cualquier configuraci�n particular.

Debe notarse que el valor de las interacciones entre los espines es fijo y depende del material; por otro lado, de acuerdo con el principio de m�nima energ�a, los espines tienden a orientarse de manera que la energ�a total del sistema, representada por H, sea m�nima. Si pudi�ramos dibujar el valor de H para cada uno de los estados posibles, tendr�amos una gr�fica en N dimensiones; en ella podr�amos observar que para algunos conjuntos de valores de {Si}, H toma valores muy altos, lo cual nos indica que dichas configuraciones ser�n muy poco probables debido a que tienen energ�as altas. De la misma manera, de acuerdo con este principio, las configuraciones o estados para los cuales H toma su valor m�nimo son los estados m�s naturales para el sistema. La figura 44 muestra de manera esquem�tica el valor de H para diferentes configuraciones.

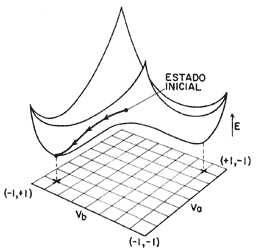
Figura 44. A partir de cualquier "estado inicial", el sistema evolucionar� hacia estados de energ�a cada vez menor.

El modelo de Ising puede ser utilizado, con mayor o menor �xito, para describir cualquier tipo de material magn�tico, siempre y cuando el conjunto de interacciones {Jij} tomen los valores adecuados. Para facilitar esta explicaci�n, vamos a considerar el caso en que no hay ning�n campo magn�tico externo; esto es, tomaremos h = 0.

Si suponemos que la interacci�n Jij toma un valor J, mayor que cero, cuando los espines localizados en los lugares i y j son contiguos, y vale cero en cualquier otro caso, entonces podemos observar lo siguiente: la configuraci�n {Si} para la cual H toma su m�nimo valor posible, se da cuando todos los espines apuntan a lo largo de la misma direcci�n; esto es, cuando todos valen +1, o equivalentemente, si todos valen -1 (v�ase la ecuaci�n (1). Si el material se encuentra en este estado, entonces todos y cada uno de los pares contribuyen a reducir el valor de la energ�a.

Ahora supongamos que Jij toma el valor -J, (con J>0), si los lugares i y j son vecinos, y el valor cero en cualquier otro caso. En esta ocasi�n, tenemos que el valor m�nimo que H puede tomar corresponde al caso en que los espines apuntan en direcciones alternadas. Esto se representa matem�ticamente con Si = +1, Sj = -1, de manera que la contribuci�n de cada par( i, j), dada por el producto Jij X Si X Sj, tiene un valor mayor que cero, con lo cual dicho par contribuir� a la reducci�n de la energ�a.

En los dos casos anteriores, si queremos construir mentalmente la configuraci�n de m�nima energ�a, entonces tenemos que una vez escogida la direcci�n de uno de los espines, la direcci�n del resto quedar� determinada.

As�, hemos visto que la ecuaci�n (1) describe materiales ferromagn�ticos o antiferromagn�ticos cuando las interacciones Jij tienen un valor mayor, o menor que cero, respectivamente. Pero, �qu� sucede si algunas interacciones tienen valores positivos y otras negativos?

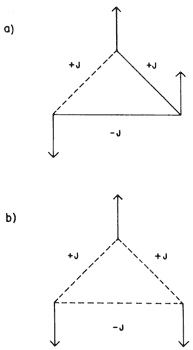
Como mencionamos anteriormente, existen algunos materiales en los cuales no es posible que todos los pares de espines contribuyan simult�neamente a reducir su energ�a. Este es el caso de los vidrios de esp�n, los cuales pueden ser descritos con la ecuaci�n (1) si algunas interacciones Jij tienen valores positivos y otras valores negativos. Esta mezcla matem�tica de interacciones positivas y negativas refleja el hecho de que a algunos pares les gusta alinearse paralelamente y a otros antiparalelamente. En estos materiales no podemos construir mentalmente una configuraci�n en la cual todos los pares de espines contribuyan a reducir la energ�a, ya que muy pronto llegaremos a contradicciones (v�ase la figura 45). Por esto no habr� una configuraci�n �nica, de energ�a m�nima. La figura 45(a) muestra una de las seis posibles configuraciones de m�nima energ�a para un sistema hipot�tico, compuesto de tan solo tres espines. En el caso de un material magn�tico con frustraci�n, el n�mero de estados de energ�a m�nima aumenta, muy r�pidamente, en funci�n del n�mero de espines (para sistemas con frustraci�n). �Y los materiales reales tienen del orden de 10²³ espines!

Pero si hay muchas configuraciones de energ�a m�nima, �cu�l de ellas ser� la que "escoja" el sistema? �Hacia cu�l de ellas evolucionar�? En las secciones subsecuentes trataremos de dar respuesta a esta pregunta.

UN CAMINANTE EN

UNA REGI�N MONTA�OSA

Supongamos que un caminante, un poco corto de vista, con muy mala memoria y muy flojo, sale a dar un paseo por el campo en una regi�n monta�osa. Sabemos que el esfuerzo que esta persona necesitar� hacer ser� mayor si asciende que si desciende. De manera que si caminara sin intenci�n de llegar a alg�n lugar en particular, esto es, de una manera un tanto azarosa, y quisiera hacer el menor esfuerzo posible, optar�a siempre por descender. Tambi�n supondremos que la �nica fuente de energ�a de este singular caminante es su energ�a potencial (= masa x gravedad x altura), y que adem�s arrastra tanto los pies que pierde toda su energ�a conforme va descendiendo. Si en un momento dado quisi�ramos dar una descripci�n de la posici�n del caminante, podr�amos proporcionar la altitud del lugar en donde se encuentra como funci�n de la latitud y la longitud de aquel lugar.

Figura 45. Este esquema nos muestra dos de los 2³ =8 posibles estados en un peque�o sistema hipot�tico compuesto por tres espines. Dos de los pares existentes interact�an ferromagn�ticamente (+J) y el tercero, antiferromagn�ticamente (-J). a) Nos muestra una de las seis configuraciones de m�nima energ�a, con H = - J (podemos observar que �nicamente un par est� frustrado). b) Nos muestra una de las configuraciones de energ�a mayor, con H = 3j; en este caso los tres pares de espines se encuentran " en desacuerdo"..

Esta persona podr�a caminar y caminar, y siempre hacia abajo, llegando a regiones cada vez m�s profundas. Por ejemplo, podr�a ir caminando dentro de un ca��n que tuviese una salida en alguna direcci�n, y probablemente esa salida lo llevar�a a regiones a�n m�s profundas. Otras veces podr�a escoger entre dos o m�s direcciones igualmente descendentes, ya que podr�a haber valles dentro de los valles, pero tarde o temprano llegar�a a un lugar profundo rodeado de regiones todas m�s altas que �ste, esto es, se encontrar�a en el fondo de un valle. El lugar final donde el caminante terminar�a su recorrido, o sea el fondo de un valle particular, depender�a de manera importante, aunque no exclusivamente, del lugar donde el explorador iniciara su caminata (Figura 46), ya que en ocasiones existen varios caminos igualmente descendentes que lo podr�an conducir a diferentes valles.

Con respecto a la geograf�a del lugar, si el sujeto no conociera la regi�n ni llevase mapas, y se encontrara en el fondo de un valle, no tendr�a manera de saber si ese valle es el lugar m�s profundo del �rea, o si m�s all� de las monta�as existen lugares a�n m�s profundos que �ste. De manera que para �l no tendr�a sentido hablar de la profundidad o altura absoluta del lugar donde se encuentra. Tampoco tendr�a forma de saber cu�ntas cimas de monta�as existen, ni cu�ntos valles, ni cu�ntos ca�ones, ni de qu� manera se encuentran �stos distribuidos. S�lo tendr�a un conocimiento local de la regi�n, ya que lo �nico que el caminador puede saber es que est� en un lugar profundo rodeado de monta�as m�s altas. Adem�s debemos tener presente que el tipo tiene muy mala memoria, por lo que es incapaz de recordar la geograf�a de los lugares previamente recorridos, y que su vista no le permite ver a lo lejos.

Una vez que el caminante se encontraba en el punto m�s bajo de un valle, tendr�a que resignarse a permanecer indefinidamente en dicho lugar. Tal vez invirtiendo un poquito de energ�a ser�a capaz de subir una peque�a colina para despu�s encontrarse con un valle mucho m�s profundo. Sin embargo esto �l no lo sabe, por lo que quedar�a atrapado a menos que sucediese alguna de las posibilidades siguientes: i) que tuviese la energ�a f�sica necesaria para hacer un esfuerzo mayor (la cual ser�a mayor cuanto m�s altas fuesen las monta�as que rodean a este lugar), o ii) que fuese rescatado y llevado a otra regi�n, por ejemplo, por un helic�ptero. Pero dado que esta persona no est� dispuesta a hacer ni el m�s m�nimo esfuerzo, pensamos que la segunda posibilidad ser�a la �nica factible.

Figura 46. El caminante llegar�, tarde o temprano, a un lugar profundo rodeado de regiones más altas.

Ahora podemos volver a pensar en la funci�n hamiltoniana y hacer una analog�a entre la geograf�a de una regi�n monta�osa y el espacio de configuraciones de un sistema f�sico con frustraci�n, ya que la hamiltoniana es tambi�n una funci�n que puede tomar valores altos o bajos, para diferentes configuraciones. Esta analog�a nos ser� �til para dar una visi�n general de las ideas presentes.

EL ESPACIO DE ESTADOS

Como dijimos anteriormente, dado un sistema magn�tico, su hamiltoniano nos da el valor de la energ�a para cada configuraci�n posible. Esto es, dada una configuraci�n o arreglo de espines es posible, en principio, calcular el valor de la energ�a correspondiente a dicha configuraci�n.²⁸ De manera que si tuvi�semos una paciencia infinita, y una vida a�n m�s larga que nuestra paciencia, podr�amos calcular la energ�a para cada uno de los estados posibles del sistema. (Este n�mero est� dado por 2ⁿ donde n es el n�mero de espines en el material, el cual es a su vez �del orden de 10²³!) En este caso, tenemos un espacio de N dimensiones, ya que podemos variar el estado de N espines, y no dos variables como en el caso del caminante en que se pueden variar su latitud y longitud �nicamente. Suponiendo que pudi�semos hacer dibujos N-dimensionales, con los resultados obtenidos podr�amos graficar el valor de la energ�a, lo que corresponder�a a la altura de las monta�as del caso anterior, como funci�n de cada uno de los estados posibles del sistema. Para completar la analog�a, dir�amos que el caminante parado en un lugar de la regi�n monta�osa corresponder�a a que el sistema magn�tico se encontrase en el estado caracterizado por el valor de todos sus espines en ese momento. De esta manera, un paso del caminante equivaldr� a invertir la direcci�n en que apunta alguno de los espines del material: si el paso es ascendente, en horizontal, o hacia abajo, esto corresponder� al aumento, mantenimiento o disminuci�n de la energ�a, para este nuevo estado.

Si colocamos al caminante en un lugar arbitrario de la regi�n y le pedimos que vague a su antojo, con la restricci�n de que haga el menor esfuerzo posible, muy probablemente �ste terminar� en el fondo del valle dentro de cuya cuenca se encontraba inicialmente. Por lo cual, para este efecto es completamente irrelevante si existen otros valles m�s profundos m�s all� de las monta�as. De la misma manera, si tenemos un vidrio de esp�n en un estado inicial arbitrario, cuya energ�a no es m�nima, entonces cada esp�n, bajo la presi�n de sus vecinos, variar� su orientaci�n de manera que su estado concuerde con la petici�n de un n�mero cada vez mayor de vecinos. As�, el sistema evolucionar� de manera natural, hasta llegar a un estado que tenga energ�a m�nima, y en el cual quedar� atrapado. La geograf�a del lugar que hemos descrito, junto con el hecho de que para ir de un estado a otro es necesario pasar por los estados intermedios, explican la gran dependencia de la historia que tienen tanto el caminante como el vidrio de esp�n, (relaci�n entre el estado inicial y el final). Esto se ilustra figura 47.

El continuo descender del caminante, o equivalentemente, el aumento en el n�mero de pares de espines que concuerdan, corresponder� a la evoluci�n natural del sistema hasta estados de energ�a cada vez menor, y por tanto, cada vez m�s probables. Decimos entonces que cada uno de los m�nimos act�a como un atractor; la importancia de un m�nimo ser� mayor mientras mas grande sea su cuenca de atracci�n. As�, veremos que un valle muy grande tiene mayor probabilidad de ser visitado que una peque�a hondonada en el camino. A los materiales ferromagn�ticos y antiferromagn�ticos les corresponde una geograf�a en la cual hay �nicamente un valle o una cuenca de atracci�n, por lo que no resulta dif�cil predecir d�nde terminara el paseo. En el primer caso, este m�nimo corresponde a un estado con todos los espines paralelos, y en el segundo, antiparalelos. Por el contrario, en el caso de los vidrios de esp�n tenemos que debido a la presencia de frustraci�n, existe un n�mero muy grande de monta�as y valles.

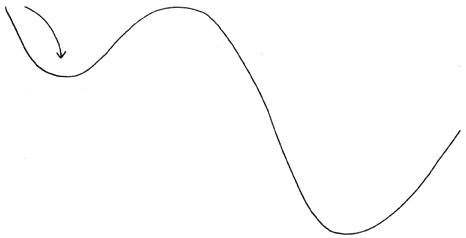
Figura 47. El sistema permanecer� en un estado de energ�a m�nima (localmente), independientemente de que existan estados de energ�a a�n menor, si para llegar a �stos necesita aumentar su energ�a.

Desafortunadamente, la imagen de una persona caminando en una regi�n monta�osa trae consigo la idea de lugar en el espacio real, lo cual puede prestarse a confusiones. Debemos recordar que en el caso del material magn�tico, su hamiltoniano nos da la energ�a como funci�n del estado del sistema, y no como funci�n de la ubicaci�n de los espines, por lo que dos estados ser�n cercanos si la mayor parte de los valores de las variables Si coinciden en ambos. Todo esto, sin importar el lugar en que se localizan dichos espines.

Otra caracter�stica de nuestro sistema magn�tico consiste en que su estado total, descrito de acuerdo con el hamiltoniano, es funci�n del estado de todos los espines. Por otro lado, dado que el n�mero de espines en el material es muy grande (del orden de 10²³, si en un momento dado se removieran algunos de ellos, sin perturbar al material de alguna otra manera, su estado general no se afectar�a de manera notable. Esta caracter�stica no tiene paralelo en nuestra descripci�n geogr�fica debido a la diferencia de la dimensi�n de ambos sistemas.

La ecuaci�n (1) nos permite obtener predicciones de algunas propiedades f�sicas del sistema por ella descrito; para lo cual, afortunadamente, no es necesario llevar a cabo el trabajo de obtener el valor de la energ�a para cada uno de los estados posibles a fin de "reconstruir la geograf�a" y despu�s encontrar los estados de energ�a m�nima. Esto se debe a que contamos, por un lado, con las herramientas de la mec�nica estad�stica,²⁹ la cual estudia las caracter�sticas globales de un sistema a partir de las caracter�sticas individuales de sus componentes, y por otro lado, con la simulaci�n num�rica (simulaci�n de una situaci�n utilizando la computadora).