VI. LA �PTICA ONDULATORIA

LA DIFRACCI�N de la luz puso a pensar a muchos cient�ficos, incluyendo a Grimaldi, su propio descubridor. La hip�tesis de los rayos rectos luminosos enfrenta, ciertamente, serios problemas l�gicos para explicar este fen�meno. �C�mo le dan la vuelta los rayos a los filos de la ranura e invaden la sombra geom�trica? �ste es s�lo uno de los principales interrogantes que se plantean.

Otro problema que resulta del fen�meno de la difracci�n en la teor�a de los rayos es la multiplicidad de las im�genes. �Por qu� se forman varias im�genes luminosas? O �por qu� los rayos trasmitidos por la ranura habr�an de preferir propagarse en unas direcciones y rehusar hacerlo en otras? (Figura 17 (b)).

Estos problemas no pueden ser resueltos por medio de la teor�a de los rayos. Para resolverlos es necesario abandonar por completo la hip�tesis de que la luz est� formada por rayos rectos. La idea cartesiana de la "especie de presi�n" que se propaga en un medio que rodea a la fuente luminosa explicar�a que la luz d� la vuelta a obst�culos, ya que esa "especie de presi�n" pasar�a por la ranura y se propagar�a en el medio que la rodea, en particular en el que est� atr�s de ella. Pero para explicar las im�genes m�ltiples es necesario suponer algo m�s.

Este "algo m�s" se sugiere de otro fen�meno �ptico que se observa haciendo pasar luz de una fuente por dos ranuras estrechas contiguas. Este experimento, llamado de la ranura doble, fue ideado por el f�sico ingl�s Thomas Young en 1815 y se puede realizar f�cilmente con los mismos elementos empleados para observar la difracci�n (Figura 16). La ranura doble se construye dividiendo longitudinalmente, con un alambre fino de cobre o un hilo de seda, una de las ranuras sencillas que se construyen fijando con durex dos hojas de afeitar, filo a filo, sobre una ranura mucho m�s ancha recortada en una tira de cartoncillo duro (Figura 21(a)). Mirando con un solo ojo a trav�s de la ranura doble la flama de una vela distante unos 5 metros, con la ranura colocada justamente frente al ojo abierto, se observa un patr�n de im�genes m�ltiples como el de la figura 21(b). En este patr�n, como era de esperarse, aparecen las im�genes laterales de difracci�n de cada una de las dos ranuras; �stas son las m�s distantes del centro. Pero m�s cerca del centro, en donde se formar�a la banda central del patr�n de difracci�n de una ranura, aparecen ahora varias im�genes m�s brillantes y detalladas que las de difracci�n. Estas im�genes m�ltiples se llaman "im�genes de interferencia" porque se obtienen s�lo si la luz proveniente de un sitio interfiere con luz similar que proviene de otro sitio; en este experimento esos sitios diferentes son las dos ranuras.

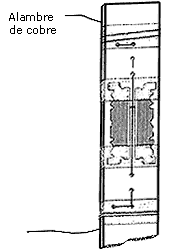
Figura 21. (a) Una ranura doble para observar el fen�meno de interferencia en la luz construida dividiendo longitudinalmente una ranura delgada por medio de un alambre fino de cobre o con un hilo fino de seda.

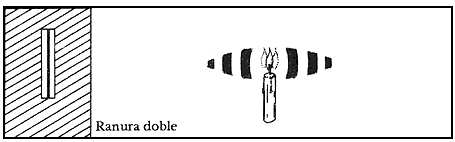
Figura 21. (b) Im�genes de interferencia de la flama de una vela, al centro, y de difracci�n, laterales, producidas por la ranura doble.

Si se hace el experimento empleando, en vez de la vela, un punto luminoso como el de la figura 19, se observan con gran nitidez varias brillantes im�genes de interferencia del punto luminoso. Si las dos ranuras y el alambre que las separa son de la misma anchura, se observan tres im�genes pr�cticamente de la misma intensidad.

Los fen�menos de interferencia son t�picos del llamado movimiento ondulatorio de un medio, como el aire o el agua. Un ejemplo com�n de movimiento ondulatorio es el que ocurre en una superficie de agua tranquila al arrojar un objeto peque�o en ella (Figura 22). El impacto del objeto produce una peque�a deformaci�n, compuesta por una depresi�n y una elevaci�n de la superficie, que aumenta de di�metro propag�ndose a su alrededor como una onda de forma circular. Las oscilaciones posteriores del agua en el sitio del impacto producen otras ondas similares que siguen a la primera a intervalos iguales de distancia y de tiempo. Si se producen ondas circulares como �stas en dos puntos cercanos del medio, en ciertos lugares suman sus efectos y producen una deformaci�n mayor de la superficie porque las depresiones y las elevaciones de las dos ondas coinciden, mientras que en otros sus efectos se cancelan porque la depresi�n de una onda coincide con la elevaci�n de la otra. En los primeros sitios se dice que las ondas interfieren constructivamente y, en los segundos, que interfieren destructivamente. Estas zonas de interferencia se pueden observar en un diagrama como el de la figura 23. En �ste, las posiciones de las ondas en cierto instante est�n representadas por los c�rculos conc�ntricos centrados en sus sitios de origen S1 y S2. Mirando el diagrama en un �ngulo oblicuo desde el extremo opuesto a S1 y S2, se distinguen unas regiones m�s oscuras que alternan con otras m�s claras; las primeras son las de interferencia destructiva, o negativa, de las ondas circulares.

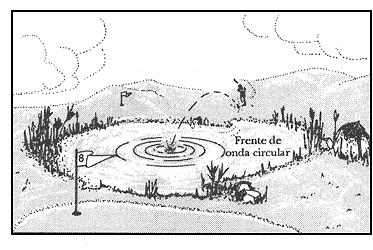
Figura 22. Ondas circulares formadas al caer un objeto peque�o en agua tranquila.

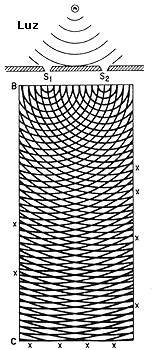
Figura 23. Diagrama de Young para observar las zonas de interferencia constructiva de ondas circulares. Viendo el diagrama en un �ngulo oblicuo desde el extremo opuesto a los centros estas zonas son las que aparecen m�s oscuras.

Este ejemplo sugiere que las im�genes de interferencia observadas en el experimento de la ranura doble resultan de la interferencia constructiva de movimientos ondulatorios que se originan en las dos ranuras. Qu� es exactamente lo que se mueve y qu� medio lo propaga no es importante por ahora; as� como no era importante en la �ptica geom�trica la naturaleza de los rayos para describir muchos fen�menos �pticos. Podemos pensar, si queremos, que lo que se mueve son zonas de esa "especie de presi�n" cartesiana, que se propagan como ondas desde cada ranura sumando sus efectos en los lugares donde se observan las im�genes de interferencia. Esto explicar�a que la luz d� la vuelta a los filos de las ranuras, as� como la aparici�n de im�genes m�ltiples de interferencia, sin que sea necesario aclarar todav�a lo que es esa "especie de presi�n". Podr�amos, incluso, llamarlas zonas de "perturbaci�n del medio", o simplemente zonas de "perturbaci�n".

Las im�genes m�ltiples de difracci�n por una sola ranura se explican muy bien tambi�n con estas ideas de la luz como un fen�meno ondulatorio. Imaginamos ahora que la ranura est� compuesta por un gran n�mero de ranuras contiguas y mucho m�s angostas, y que cada una de ellas produce ondas de perturbaci�n del medio al mismo ritmo que las dem�s. Combinando los efectos de estas ondas en cada punto atr�s de la ranura, sum�ndolos o rest�ndolos seg�n tengan la misma direcci�n o direcciones opuestas al llegar a ese punto, se encuentran zonas de mayor o de menor perturbaci�n que corresponden exactamente con las de iluminaci�n y de sombra observadas visualmente o con una fotograf�a. As� pues, es tambi�n la interferencia de ondas, aunque de muchas ondas, la causante del patr�n de difracci�n, y el "algo m�s" que busc�bamos para explicarlo es el movimiento ondulatorio de las zonas de perturbaci�n del medio.

La �ptica ondulatoria, o teor�a ondulatoria de la luz, naci� de analog�as como �stas entre fen�menos �pticos y fen�menos propios de movimientos ondulatorios conocidos como el de las ondas en l�quidos, o el a�n m�s conocido de las ondas ac�sticas que producen el sonido. Un movimiento ondulatorio muy simple se puede observar en una manguera de jard�n fija a la pared por un extremo y movida r�tmicamente hacia arriba y hacia abajo por el extremo suelto al tiempo que se le mantiene tensa (Figura 24). Cada oscilaci�n produce en la manguera una joroba que avanza hacia el extremo opuesto seguida por otras jorobas an�logas a intervalos iguales de distancia y de tiempo, tal y como ocurre con las ondas circulares en la superficie del agua. Estas ondas se llaman ondas el�sticas porque se propagan en un medio el�stico como es el hule de la manguera.

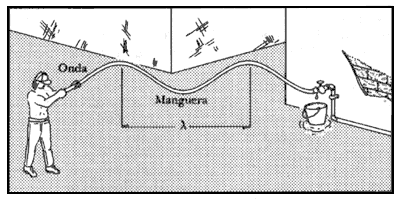
Figura 24. Ondas el�sticas en una manguera de jard�n.

El tiempo que toma generar una joroba completa se llama periodo y es igual al tiempo necesario paa ejecutar la oscilaci�n completa del extremo suelto por la manguera. La distancia horizontal que ocupa una joroba completa se llama longitud de onda. Como cada joroba avanza una longitud de onda en el transcurso de un periodo, la velocidad de avance de la onda es igual a la longitud de onda dividida entre el periodo; por ejemplo, si cada joroba ocupa una longitud horizontal de 0.6 m, y el tiempo de cada oscilaci�n del extremo suelto de la manguera es de 2 s, la longitud de onda es de 0.6 m, el periodo es de 2 s y la velocidad de avance de la onda es de 0.6 m/ (2s) = 0.3 m/s. El n�mero de jorobas que se producen cada segundo es igual al n�mero de oscilaciones que se den, cada segundo, al extremo suelto de la manguera. Esta cantidad se llama frecuencia de la onda y se puede obtener dividiendo la unidad entre el periodo; en el ejemplo anterior la frecuencia es igual a 1/ (2s) = 0.5/s, o bien, 0.5 Hz (l�ase hertzios). Se comprueba f�cilmente que la velocidad de avance de la onda se obtiene tambi�n multiplicando la longitud de onda y la frecuencia; en este ejemplo, se tiene: velocidad = 0.6 m X 0.5 Hz = 0.3 m/s.

El sonido es un movimiento ondulatorio que se propaga en el aire y en otros medios materiales. Por ejemplo, al sonar una campana sus vibraciones producen, alternadamente, zonas de compresi�n y de expansi�n del aire que la rodea. Estas zonas se propagan en forma parecida a la de las ondas circulares del agua, pero como pueden hacerlo en todas direcciones forman una onda esf�rica (Figura 25). La distancia entre dos zonas consecutivas de compresi�n o de expansi�n del aire es la longitud de onda y la frecuencia de vibraci�n de la fuente es tambi�n la frecuencia de la onda. Estas ondas se llaman, en general. ondas sonoras o ac�sticas. Su velocidad de propagaci�n en aire es de 330 m/s aproximadamente. Al llegar al o�do hacen vibrar el t�mpano y si la frecuencia de vibraci�n est� comprendida entre unos 20 Hz y unos 16 000 Hz producen la sensaci�n de sonido. La longitud de onda est� comprendida entre (330 m/s) / (20 Hz) = 16.5 m y (330m/s) / (16 000 Hz) = 0.021 m = 2.1 cm.

Figura 25. Ondas esf�ricas de compresi�n y de expansi�n del aire producidas por las vibraciones de una campana. Se propagan a la velocidad del sonido, 330 m/s.

Todos los movimientos ondulatorios producen fen�menos an�logos. Por ejemplo, el sonido se refleja en paredes s�lidas en forma an�loga a la reflexi�n de la luz en espejos; este fen�meno se llama eco. El sonido da la vuelta a obst�culos en forma an�loga a la difracci�n de la luz; por esto se pueden o�r conversaciones alrededor de una esquina, y de una habitaci�n a otra si una puerta intermedia est� abierta. El sonido tambi�n produce fen�menos de interferencia. Cuando suenan dos notas musicales muy parecidas se escuchan f�cilmente modulaciones de su intensidad, llamadas batimientos, que resultan de la interferencia de las ondas que las notas producen.

Estas analog�as entre fen�menos �pticos y ac�sticos fueron demostradas por los experimentos con ranuras realizados por Thomas Young hacia 1815 y dieron una gran fuerza a la hip�tesis de que la luz, como el sonido, es un fen�meno ondulatorio que resulta de ondas esf�ricas que se producen en cada punto de los cuerpos luminosos y se propagan en los medios transparentes, como el aire, el agua, el vidrio o el vac�o. �sta es la hip�tesis fundamental de la �ptica ondulatoria y con ella es posible entender fen�menos �pticos inexplicables con la teor�a de rayos, sin que sea siquiera necesario en muchos casos precisar la naturaleza de las ondas luminosas; es decir, sin que sea necesario precisar la propiedad del medio que es perturbada y que se propaga en forma de ondas luminosas. Por ejemplo, se pueden calcular los �ngulos de desviaci�n de la luz difractada por una ranura conociendo solamente la anchura de la ranura y la longitud de onda de la luz, sin que sea necesario precisar la propiedad del medio que constituye las ondas luminosas. As�, el �ngulo de desviaci�n de la luz que forma la primera imagen lateral se calcula con la f�rmula �=38.2 (L/a); siendo "L" la longitud de onda de la luz y "a" la anchura de la ranura. Desde luego, tambi�n se puede calcular la longitud de onda de la luz difractada y de la anchura de la ranura utilizando la f�rmula anterior en la forma L = (� / 38.2)a. Por ejemplo, si la anchura de la ranura es de 0.001cm y el �ngulo de desviaci�n de la luz que forma la primera imagen lateral es de1.9�, la longitud de onda de la luz es L = (1.9�/ 38.2) X 0.001=0.00005 cm. De manera similar Thomas Young midi� la longitud de onda de la luz de cada color del arco iris encontrando que son diferentes. La de la luz roja, por ejemplo, es de unos 0.000075 cm; la de la amarilla es de unos 0.000060 cm y la de la luz violeta de 0.000040 cm.�entre 100 000 y 1 000 000 de veces m�s peque�as que las longitudes de onda de las ondas ac�sticas! La frecuencia de las ondas luminosas se pudo calcular tambi�n f�cilmente porque la velocidad de la luz, 300 000 km/s=30 000 000 000 cm/s, ya era conocida. Para la luz amarilla la frecuencia resulta ser de 30 000 000 000 cm/s)/(0.000,060cm) = 50 000 000 000 000 Hz. Esta frecuencia es miles de millones de veces mayor que la de las ondas ac�sticas. Las cantidades muy, muy peque�as y las muy, muy grandes hac�an su aparici�n en la f�sica.

Los experimentos de Thomas Young dieron una gran fuerza a la hip�tesis ondulatoria de la luz pero no fueron su origen. Las ideas ondulatorias de la luz surgieron simult�neamente con las corpusculares de Newton, muy posiblemente inspiradas en las ideas cartesianas de la "especie de presi�n" propagadas en un medio. Su principal proponente fue el f�sico holand�s, contempor�neo de Newton, Hans Christian Huygens, alrededor de 1670. Sin embargo, Huygens dedic� su teor�a ondulatoria de la luz principalmente a explicar problemas de reflexi�n y de refracci�n de la luz como los llamados fen�menos de refracci�n atmosf�rica; por ejemplo, la aparici�n de espejismos, el parpadear de las estrellas o la aparente deformaci�n del disco de la Luna o del Sol cuando est�n cerca del horizonte.

Huygens explic� estos fen�menos a partir de la hip�tesis ondulatoria principal de que un punto luminoso produce ondas esf�ricas y de que �stas estimulan la vista s�lo si la mirada se dirige a lo largo del radio de las ondas esf�ricas que llegan al ojo; o sea, s�lo si se dirige la vista hacia el punto luminoso. Esta segunda parte de la hip�tesis es necesaria para incluir la propagaci�n rectil�nea de la luz (Figura 26). En muchos fen�menos las ondas cambian de forma por distintas razones y dejan de ser esf�ricas, por lo que no se puede hablar del radio de la esfera. Se supone entonces que la onda estimula la vista si la mirada se dirige a lo largo de la perpendicular a la zona de perturbaci�n que est� en contacto con el ojo (Figura 27). Esto no cambia la hip�tesis principal porque si la onda es esf�rica, la perpendicular y el radio tienen la misma direcci�n.

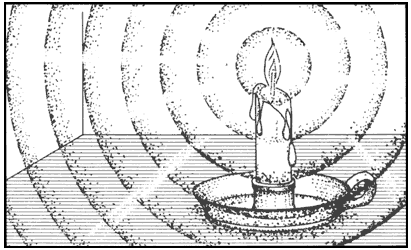
Figura 26. La hip�tesis principal de la �ptica ondulatoria es que cada punto luminoso produce ondas esf�ricas.

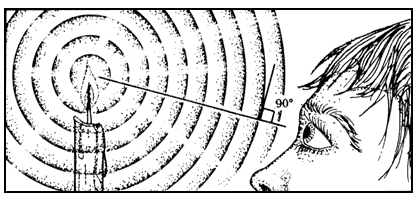
Figura 27. Si la mirada se dirige en direcci�n perpendicular a las zonas de perturbaci�n se estimula el sentido de la vista. En las ondas esf�ricas esta direcci�n coincide con un radio de la esfera.

Para explicar los fen�menos de refracci�n atmosf�rica se hacen diagramas en los que las ondas esf�ricas se representan mediante c�rculos conc�ntricos centrados en el punto luminoso que las produce (Figura 28). La distancia entre c�rculos consecutivos representa la longitud de onda a una cierta escala de dibujo; por ejemplo, 1cm podr�a representar una longitud de onda de 0.000050cm.

Figura 28. La separaci�n entre las zonas esf�ricas y la longitud de onda cambia de un lugar a otro si la velocidad de propagaci�n cambia.

Si la longitud de onda cambiara en alg�n lugar representado en el diagrama, por ejemplo, porque cambiara la velocidad de propagaci�n de las ondas, la distancia entre los c�rculos conc�ntricos tambi�n se alterar�a en los puntos del diagrama correspondientes a ese lugar.

Un espejismo es la reflexi�n aparente de cuerpos en el suelo, como si existiera un espejo de agua (Figura 29). Se observa en d�as muy soleados, cuando el aire que est� en contacto con la superficie terrestre se calienta mucho m�s que el que est� en capas superiores. El aire caliente de abajo se dilata y se hace menos denso que el aire m�s fr�o de arriba. Esto, a su vez, disminuye continuamente el �ndice de refracci�n del aire desde las capas superiores hasta la que est� en contacto con el suelo. La luz emitida desde un objeto hacia el suelo cambia su direcci�n de propagaci�n tambi�n continuamente y termina recorriendo un camino curvo que la dirige finalmente hacia arriba, como se muestra en la figura 29. Un observador ve el objeto en la direcci�n que tiene la luz cuando llega a su ojo; o sea, la ve en la direcci�n general del suelo, como si ah� se hubiera reflejado la luz del objeto.

Figura 29. Un espejismo es la reflexi�n aparente de cuerpos, como si existiera un espejo de agua en el suelo. Se observan en d�as muy asoleados y se deben al calentamiento de la capa de aire en contacto con el suelo.

Si representamos las ondas luminosas emitidas por un punto del objeto por medio de c�rculos conc�ntricos, la distancia entre c�rculos consecutivos debe cambiar de uno a otro porque la velocidad de propagaci�n de la luz tambi�n cambia de una capa de aire a otra. Si la distancia entre c�rculos aumenta de los superiores a los inferiores, la direcci�n de la perpendicular a los c�rculos, que es la direcci�n de propagaci�n de la luz, se curva hacia arriba como se muestra en la figura 30 (a); pero si la distancia entre c�rculos disminuye, la direcci�n de propagaci�n se curva hacia abajo como se muestra en la figura 30 (b). Los espejismos se forman porque la direcci�n de propagaci�n se curva hacia arriba cuando el aire se hace menos denso. Esto demuestra, entonces, que si la luz es un fen�meno ondulatorio su velocidad de propagaci�n debe ser mayor en los medios menos densos y alcanzar�a su valor m�ximo cuando la densidad fuera nula; o sea, en el vac�o.

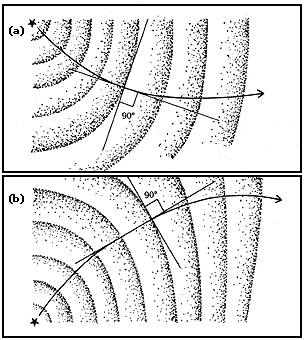
Figura 30. (a) La direcci�n de propagaci�n de la luz se curva hacia arriba si su velocidad aumenta en las capas inferiores. (b) La direcci�n de propagaci�n de la luz se curva hacia abajo si su velocidad disminuye en las capas inferiores.

Esta conclusi�n de la teor�a ondulatoria sobre la velocidad de la luz en medios de densidades diferentes se opone completamente a la obtenida con la hip�tesis corpuscular de Newton, la cual afirma que la velocidad de propagaci�n es mayor en el medio m�s denso. La controversia entre las dos teor�as hubiera podido ser dirimida midiendo la velocidad de la luz en medios de distintas densidades, por ejemplo en aire y en agua; pero la velocidad de la luz es tan grande que en tiempos de Huygens y Newton no era posible hacer esta medici�n mas que por m�todos astron�micos y s�lo se conoc�a su valor en el vac�o, que es aproximadamente igual a 300 000 km/s. La controversia dur� cerca de 150 a�os, hasta que los experimentos de difracci�n y de interferencia hechos por Thomas Young en 1815 dieron tanto apoyo a las ideas ondulatorias que la medici�n de las velocidades de la luz en distintos medios perdi� algo de su importancia para dirimir la controversia. Sin embargo, en 1850 el f�sico franc�s Jean B. Foucault pudo medir la velocidad de la luz en agua encontrando un valor 33% menor que en aire. La teor�a corpuscular de Newton parec�a estar definitivamente muerta.