IV. EL CAMPO GEOMAGNÉTICO, UN ANALIZADOR DE RAYOS CÓSMICOS

PARA interpretar cualquier medición de la intensidad de la radiación cósmica que se realice cerca de la superficie de la Tierra se requiere conocer la forma como el medio ambiente terrestre la afecta. El primer factor que debe ser tomado en cuenta es la presencia del campo magnético terrestre.

Como veremos más adelante, una de las consecuencias de la existencia del campo geomagnético es que no todas las partículas que llegan a sus inmediaciones pueden penetrar hasta la superficie de nuestro planeta. El "precio de admisión" es mas bajo conforme nos acercamos a los polos, lo cual da origen al conocido efecto latitudinal. Además, el campo se comporta como un complicado sistema de lentes que impone ciertas restricciones a las direcciones desde las cuales los rayos cósmicos pueden arribar a un punto dado.

A diferencia de un telescopio óptico o un radiotelescopio, que detectan radiación electromagnética, la cual no es afectada por campos magnéticos y por tanto viaja en línea recta, un telescopio de rayos cósmicos no "ve" en la dirección que apunta. Las partículas cargadas son sometidas por el campo geomagnético a diversos movimientos de giro en su camino hacia la Tierra, así pues la dirección de acercamiento puede resultar muy distinta de aquella a la cual apunta el instrumento.

La forma y magnitud del efecto del campo geomagnético sobre los rayos cósmicos primarios es el tema del presente capítulo. Pero antes de entrar en materia es necesario analizar brevemente el campo magnético de la Tierra, así como los efectos de campos magnéticos más sencillos sobre partículas cargadas.

UN IMAN DEL TAMAÑO DE LA TIERRA

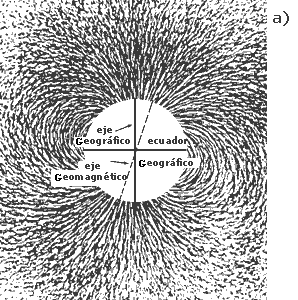
El campo magnético terrestre se parece mucho al producido por una pequeña barra de imán. La manera más sencilla de conocer la forma de este campo es mediante el empleo de limaduras de hierro. Estas limaduras se colocan, formando una capa uniforme, sobre un trozo de cartulina lisa o de papel y debajo de éste se coloca un imán. Las limaduras de hierro se imanan y se orientan siguiendo las líneas de fuerza magnética [Figura 7 (a)]. A este campo se le conoce también como campo dipolar o simplemente dipolo. Un campo dipolar no es un campo uniforme puesto que las líneas de fuerza se curvan y su intensidad decrece con la distancia al centro del dipolo. Para una distancia dada el campo será más débil en el ecuador y más fuerte hacia los polos. El eje del dipolo terrestre está inclinado 11° con respecto al eje de rotación [Figura 7 (b)].

En realidad el campo geomagnético no es exactamente el de un dipolo; la existencia de muchos sistemas de corrientes en el interior de la Tierra hace que, para una representación precisa del campo, sea necesario utilizar un desarrollo de multipolos de Gauss: una expresión matemática en donde se considera al dipolo como el primer término de una serie. Los términos no dipolares sólo son importantes en las cercanías de la Tierra, por lo que a grandes distancias la forma del campo es dipolar.²²

La componente externa más importante del campo geomagnético es la debida a la presencia del viento solar (véase el capítulo VII), un plasma tenue que fluye a velocidades supersónicas y que al interactuar con el campo geomagnético interno lo "comprime" del lado día y lo "estira" del lado noche. De esta manera se genera una cavidad que separa magnéticamente el espacio circunterrestre del medio interplanetario. A esta cavidad se le conoce como magnetósfera. Una representación esquemática de la magnetósfera se muestra en la figura 8.

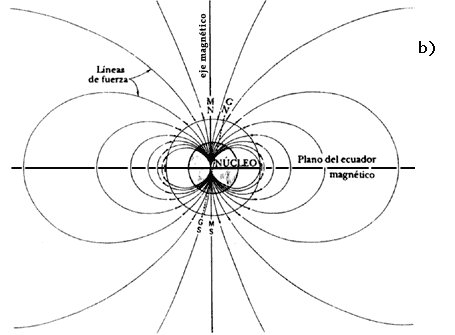Figura 7. (a) El campo magnético de la tierra se ilustra aquí por medio del patrón que muestran las limaduras de hierro alrededor de una simple barra de imán. (b) Las líneas de fuerza del campo magnético dipolar de la Tierra se muestran aquí en un corte transversal que pasa a través del eje magnético. La letra M designa magnético; la G, geográfico. Las flechas en la superficie de la Tierra muestran la orientación de una brújula. Puede verse la inclinación entre el eje magnético y el geográfico.

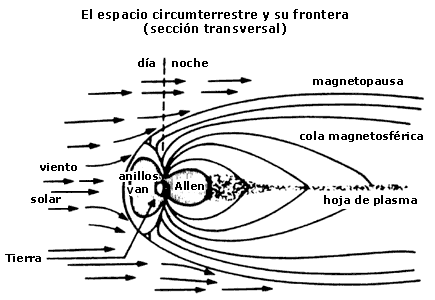
Figura 8. Magnetósfera terrestre y espacio circunvecino. En la figura se muestra la frontera entre esos dominios: la magnetopausa, así como los anillos de Van Allen y la llamada cola magnetosférica.

Como se puede ver en la figura, la forma real del campo geomagnético es muy similar a la de un cometa, aun cuando el proceso físico por el cual se generan sea distinto, pues los cometas no poseen campos magnéticos propios y en este caso la interacción del viento solar es directamente con su atmósfera.

CAMPOS Y CARGAS

Cuando una partícula cargada se mueve en presencia de un campo magnético experimentará una fuerza deflectora, la fuerza de Lorentz, que actúa perpendicularmente tanto a la dirección de propagación como a la dirección del campo magnético. Si el campo resulta ser uniforme y perpendicular a la dirección de movimiento, la partícula se moverá formando un círculo. El radio p de este círculo será directamente proporcional a la cantidad de movimiento p de la partícula e inversamente proporcional a la intensidad del campo B. Esto es, dada una especie de partículas (p. ej.: protones), las más rápidas tendrán radios de giro mayores en un cierto campo, pero si la intensidad magnética aumenta los radios de giro tenderán a hacerse más pequeños. Partículas de mayor masa (p. ej.: partículas a) que se muevan a la misma velocidad describirán círculos mayores puesto que su cantidad de movimiento (mv) es mayor debido a que tienen mayor masa. Por otro lado, partículas con carga negativa (p. ej.: electrones) girarán en sentido opuesto al de las partículas con carga positiva.

Al producto Bp se le denomina rigidez magnética de la partícula y está dada por la expresión (véase el Apéndice C):

donde p = mv es la cantidad de movimiento de la partícula y Z su carga eléctrica en unidades de e: la carga del electrón. Como el radio de curvatura es proporcional a la cantidad de movimiento, la cantidad p / (Ze) puede ser considerada como una medida de la resistencia de la partícula a ser desviada por el campo.

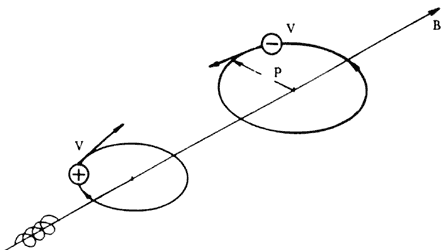
Figura 9. Movimiento de partículas cargadas en un campo magnético. Si el radio de giro p es pequeño, la partícula es obligada a seguir la línea de fuerza.

En general, la dirección de propagación de una partícula cargada no es perpendicular al campo magnético. En este caso, como la componente de la velocidad paralela al campo no es afectada por B, la trayectoria será una hélice (Figura 9).

Ahora bien, ¿qué sucede cuando las cargas se mueven en un campo no homogéneo como es el caso del campo de la Tierra? En este caso los movimientos serán más complicados y aunque no vamos a entrar en detalles describiremos a continuación los efectos más importantes.

UN LARGO Y SINUOSO CAMINO

En la figura 10 se muestra la trayectoria de una partícula de la radiación cósmica en el campo geomagnético. Como puede apreciarse, ésta es muy complicada y para determinar teóricamente su forma es necesario recurrir a la ayuda de las computadoras.

Figura 10. Trayectoria de un protón casi atrapado en el campo magnético terrestre después de llegar de una fuente distante. Es claro que si dicha partícula llega eventualmente a la superficie, su dirección aparente de llegada no tiene nada que ver con la que traía originalmente.

Cuando se trata el problema de la propagación de los rayos cósmicos a través de campos magnéticos resulta conveniente caracterizar a las partículas por su rigidez magnética Bp puesto que partículas con la misma Bp seguirán trayectorias idénticas. Por otro lado, para enfrentar el problema en forma correcta es necesario seguir las trayectorias en sentido inverso. Esto es, suponer que una partícula de carga opuesta sale desde el punto de interés y analizar si finalmente ésta llega a la frontera del campo geomagnético, o si por el contrario la trayectoria analizada regresa a la superficie terrestre. En el primer caso se dirá que la trayectoria es permitida, pues un rayo cósmico podría haberla seguido para penetrar hasta la Tierra; en el segundo, esto no sería posible y se hablará entonces de una trayectoria prohibida. El primero que estudió el problema del movimiento de partículas cargadas en un dipolo magnético fue el matemático y geofísico noruego C. Störmer, quien estaba interesado en estudiar las auroras boreales o luces del norte, como se conoce al espectacular fenómeno que se da en las altas latitudes de la Tierra. Störmer creía que las auroras son causadas por partículas emitidas por el Sol a consecuencia de su actividad. Después de largos y tediosos cálculos numéricos, Störmer pudo llegar a conclusiones de carácter general respecto al comportamiento de las partículas.

Aun cuando los rayos cósmicos poseen energías mucho mayores que las de las partículas aurorales y llegan a la Tierra desde todas direcciones y no sólo desde el Sol, algunas de las conclusiones de Störmer resultaron ser aplicables al caso: para cada punto en la Tierra y para partículas positivas de una rigidez dada existe un cono (cono de Störmer) de direcciones prohibidas, cuyo eje apunta hacia el este. De esta manera, si los rayos cósmicos son partículas cargadas positivamente llegarán a la Tierra en menor número desde el este del firmamento que de las regiones del oeste. Si por el contrario las partículas tienen carga negativa el cono apuntará hacia el oeste y la situación es la opuesta. Esta asimetría llegó a conocerse como efecto este-oeste (Figura 11).

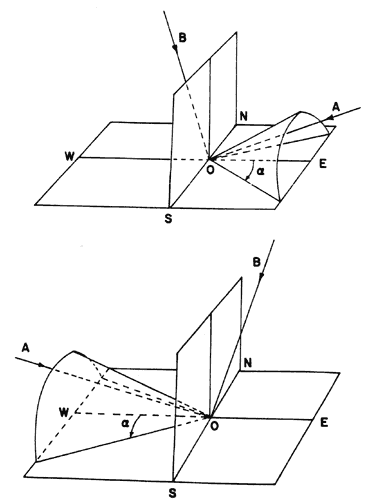
Figura 11. Conos Störmer para partículas positivas (a) y negativas (b) de la misma rigidez magnética. En ambos casos las direcciones AO son prohibidas y las BO son permitidas. Para partículas positivas el cono apunta hacia el este y para negativas hacia el oeste. El ángulo a es la mitad del ángulo de apertura de los conos.

Hasta ese momento no se había establecido aún la naturaleza de los rayos cósmicos primarios (los que inciden sobre el tope de la atmósfera); se sabía que eran partículas cargadas, pero no cuál era la carga de éstas: positiva o negativa. Ello motivó la realización de una serie de experimentos para comprobar la existencia de un efecto este-oeste. Al encontrarse que la radiación cósmica llega preferentemente de direcciones al oeste del punto de observación, se estableció definitivamente su naturaleza corpuscular y se supo además que la mayoría de estas partículas poseen carga positiva (véase también el capítulo v).

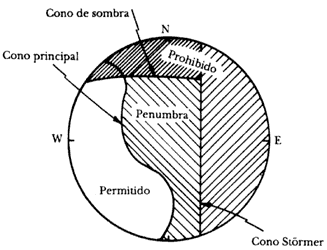
Figura 12. Regiones prohibidas (oscuras) y permitidas (claras) para partículas de 10 GV.

El conocimiento de la existencia de un cono de direcciones prohibidas para cada tipo de partículas sirvió para resolver el problema de la naturaleza de los rayos cósmicos; sin embargo, la teoría de Störmer no tomaba en cuenta las complicaciones introducidas por la presencia de la Tierra como un cuerpo sólido de dimensiones apreciables dentro del campo magnético.

El mexicano M. Sandoval Vallarta y el belga O. Lemaitre, después de complicados cálculos numéricos, encontraron que algunos ángulos fuera del cono de Störmer, aun cuando no correspondían a direcciones prohibidas, cruzaban la Tierra en algún punto de su trayectoria y establecieron así la existencia de un cono de sombra en el cual algunas direcciones de acercamiento son prohibidas y otras permitidas. Las diversas zonas de direcciones de acercamiento para partículas positivas con una rigidez magnética de 10 GV que arriban a una latitud de 30° HolNorte se muestran en la figura 12.

EL EFECTO LATITUDINAL

Consideremos ahora lo que sucede si apuntamos un detector de rayos cósmicos hacia una dirección determinada, supongamos que esta dirección es el cenit (la vertical). Veremos que el detector recibe todas las partículas de rigideces altas, como si el campo geomagnético no estuviera presente. Si medimos cada vez el flujo de rigideces magnéticas menores veremos que existe una rigidez debajo de la cual no se detecta partícula alguna, a ésta se le conoce con el nombre de rigidez umbral. Para cada punto de la Tierra, cada dirección de acercamiento, época del año y tiempo local existe una rigidez umbral; como ésta se encuentra determinada por la presencia del campo geomagnético se le conoce también como umbral geomagnético. Si desplazamos nuestro detector vertical desde el ecuador hacia los polos observaremos que la rigidez umbral se va haciendo cada vez menor, es decir, partículas con rigideces pequeñas que no pueden alcanzar puntos sobre la Tierra a bajas latitudes podrán llegar a ésta a latitudes mayores. Este fenómeno se conoce como efecto latitudinal y se encuentra ilustrado en la figura 13.

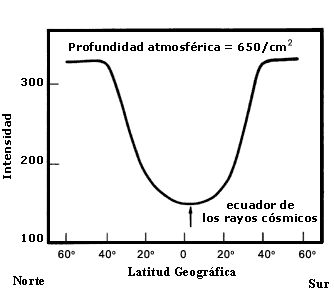
Figura 13. Efecto latitudinal en la intensidad de la radiación cósmica de acuerdo a los estudios teóricos de Lemaitre y Vallarta. Cada curva se refiere a partículas de una rigidez magnética en partículas y da el número total de dichas partículas que llegan al tope de la atmósfera como función de la latitud geomagnética.

En la figura 14 se muestran algunos conos de direcciones permitidas para diversas estaciones de rayos cósmicos alrededor del mundo, las que se obtuvieron al usar un modelo dipolar del campo geomagnético. En ellos puede apreciarse la importancia de las estaciones polares, pues son éstas las que pueden ver en direcciones alejadas del ecuador celeste, además de que sus conos están poco abiertos y por tanto "apuntan" en forma más precisa a ciertas regiones del cielo.

Las predicciones de Sandoval Vallarta y Lemaitre no coinciden, sin embargo, con las mediciones hechas posteriormente. Las discrepancias se deben, como ya mencionamos, a varias razones:
1) El eje del dipolo terrestre no se encuentra alineado con el eje geográfico.
2) Existen contribuciones de términos no dipolares al campo geomagnético.
3) La presencia del viento solar altera la forma del campo geomagnético comprimiéndolo del lado día y estirándolo del lado opuesto.

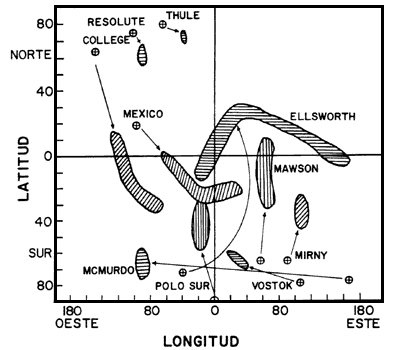
Figura 14. Conos asimptóticos de aceptación de varios monitores de neutrones en la esfera celeste pero en coordenadas geográficas. Las estaciones están localizadas en los puntos marcados con una Å.

Este último hecho trae como consecuencia que las características de los rayos cósmicos recibidos en un punto sobre la Tierra dependan de la hora local de observación, ya que durante el día la Tierra gira en el interior de la magnetósfera, la cual no es simétrica.

Trabajos teóricos efectuados en las décadas de los sesenta y los setenta, a los cuales contribuyeron de manera significativa investigadores mexicanos, incluyen los efectos enumerados. Éstos permiten precisar en buena medida los conos de direcciones permitidas para cada punto sobre la superficie de la Tierra y reproducen con bastante fidelidad los efectos observados. Los efectos geomagnéticos sobre los rayos cósmicos son hoy en día conocidos con bastante precisión.

Para llegar al conocimiento actual en este campo fue necesario tanto el ingenio de los que propusieron diversos modelos matemáticos para representar el campo geomagnético, como el trabajo tesonero de quienes hicieron innumerables cálculos, y el espíritu aventurero de los físicos experimentales que tuvieron que recorrer el mundo de polo a polo en diversas ocasiones llevando consigo sus detectores y teniendo que sortear las múltiples dificultades que ello significaba. En la actualidad existe una red mundial de aproximadamente 50 estaciones que detectan la radiación cósmica, una de ellas en la ciudad de México a cargo del Departamento de Física Espacial del Instituto de Geofísica de la UNAM.