XIV. MAXWELL. LA S�NTESIS DEL ELECTROMAGNETISMO. OTRA VEZ LA LUZ

EL ESCOC�S James Clerk Maxwell (1831-1879), alumno de Faraday, fue posiblemente el m�s imaginativo de los f�sicos del siglo XIX. En 1873 public� la monumental obra Tratado de electricidad y magnetismo, en la que present� una s�ntesis de los conocimientos de este tema. Maxwell formul� matem�ticamente la ley de Faraday. La s�ntesis fue hecha en t�rminos de un conjunto de ecuaciones, conocidas como las ecuaciones de Maxwell, que conten�an corno fondo f�sico los descubrimientos de Oersted, Amp�re, Faraday y otros cient�ficos que describimos en cap�tulos anteriores. El gran f�sico vien�s Ludwig Boltzmann exclam� al leer las ecuaciones de Maxwell: "�Fue un Dios quien traz� estos signos?", usando las palabras de Goethe.

Maxwell estudi� con mucho detenimiento los trabajos que sus predecesores hab�an hecho sobre electricidad y magnetismo. En particular analiz� muy incisivamente la ley de Amp�re y su formulaci�n matem�tica, y lleg� a la conclusi�n de que conten�a una contradicci�n. Revisemos la ley de Amp�re.

Consideremos una l�nea curva cerrada, arbitraria como la que se muestra en la figura 27 con la letra C. Ahora sup�ngase que una superficie como la S, que no es cerrada, tiene sus extremos precisamente en la l�nea C. Fuera de esta restricci�n la superficie S puede ser la que sea. La ley de Amp�re se puede formular diciendo que el campo magn�tico a lo largo de la l�nea C depende solamente de la corriente el�ctrica que cruce la superficie S.

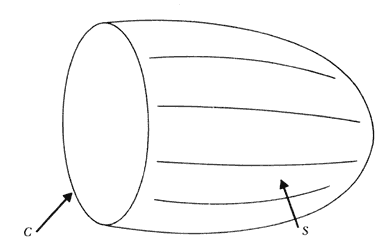
Figura 27. La superficie S tiene sus extremos en la l�nea cerrada C.

Para apreciar la contradicci�n que contiene la formulaci�n hecha por Amp�re consideremos el caso de un condensador de placas paralelas que est� conectado a una bater�a por medio de alambres conductores (Figura 28). Este tipo de condensador es un dispositivo que consiste en dos placas met�licas separadas a cierta distancia fija. Entre estas placas puede haber aire o bien alguna sustancia que no conduzca electricidad; consideremos el caso cuando hay aire. Antes de cerrar el interruptor de circuito no hay corriente el�ctrica y por lo tanto no se genera ning�n campo magn�tico alrededor de los alambres conductores. Desde el momento en que el interruptor se cierra empieza a fluir una corriente el�ctrica que va cargando paulatinamente las placas del condensador hasta que alcanzan su m�xima capacidad. Una vez cargadas, como la corriente no puede atravesar el espacio entre las placas, deja de fluir, o sea que nuevamente es nula, a pesar de que el interruptor est� cerrado. Una vez que se llega a este estado, como no hay corriente tampoco se genera campo magn�tico alguno. Maxwell intent� calcular el campo magn�tico generado en el intervalo transitorio en que s� hay corriente. Para ello us� la formulaci�n matem�tica de la ley de Amp�re arriba mencionada. En primer lugar, consider� una l�nea C que rodea el cable (Figura 28); en seguida consider� una superficie como la S, que tiene su extremo en C y que cruza el cable. De esta forma obtuvo cierto valor no nulo para el campo magn�tico generado por la corriente a lo largo del cable, ya que la superficie S es atravesada por una corriente el�ctrica. A continuaci�n consider� otra superficie, la S' mostrada en la figura, cuyo extremo coincide con la l�nea C, pero que se cierra a trav�s del espacio entre las placas del condensador. En este caso, ninguna corriente cruza la superficie S' y de acuerdo con la ley de Amp�re, a lo largo de la l�nea C no hay ning�n campo magn�tico. Entonces, �hay o no hay campo magn�tico? Al usar la superficie S se predice que s� lo hay, mientras que si se usa la superficie S' se predice que no lo hay. Por supuesto que la existencia de un campo magn�tico no debe depender de c�mo nosotros escojamos la superficie con extremo en C.

Maxwell resolvi� esta contradicci�n de la siguiente forma: sab�a que la existencia de una corriente el�ctrica a lo largo del cable se debe a que hay un voltaje entre los extremos, causado por la bater�a, que produce un campo el�ctrico dentro del cable. Este campo hace que part�culas cargadas se muevan y produzcan una corriente el�ctrica. Por otro lado, cuando las placas del condensador tienen cargas el�ctricas se genera entre las placas un campo el�ctrico. En el intervalo en que se est� cargando el condensador, el valor de las cargas en sus placas est� cambiando con el tiempo, con la consecuente variaci�n del campo el�ctrico. Una vez que el condensador se ha cargado a su m�ximo valor y las cargas en sus placas ya no cambian, entonces el campo entre ellas tampoco cambia y adquiere un valor constante con el tiempo. Maxwell formul� la siguiente hip�tesis: si entre las placas del condensador el campo el�ctrico var�a con el tiempo, esta variaci�n es equivalente a la existencia de una corriente el�ctrica, a la cual llam� de desplazamiento. De esta forma, durante el intervalo en que se cargan las placas del condensador, a la superficie S' de la figura 28 s� la atraviesa una corriente, la de desplazamiento, y por tanto s� se genera un campo magn�tico a lo largo de la l�nea C. Bas�ndose en su hip�tesis, y a partir de un detallado an�lisis matem�tico, Maxwell encontr� que el campo magn�tico que se obtiene al usar S es el mismo que resulta cuando se emplea la superficie S'; por lo que la contradicci�n desaparece.

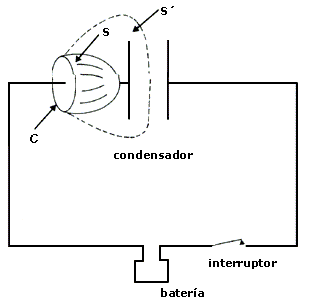
Figura 28. La superficie S, para obtener el campo magn�tico que crea el alambre conductor, cruza el alambre. La superficie S' no cruza el alambre conductor sino que se cierra dentro del condensador.

Maxwell generaliz� la formulaci�n de la ley de Amp�re al decir que cuando se habla de corriente se debe incluir la corriente convencional (llamada de conducci�n), que es la que hab�a considerado Amp�re, y adem�s, la corriente de desplazamiento. Por lo tanto, esta generalizaci�n incluye casos en que las corrientes var�an con el tiempo. Podemos decir que la formulaci�n original que hizo Amp�re s�lo es correcta para el caso en que la corriente que se estudia no var�e con el tiempo.

La hip�tesis hecha por Maxwell tuvo consecuencias trascendentales. En primer lugar, se sabe de los trabajos de Faraday que si un campo magn�tico cambia con el tiempo se induce un campo el�ctrico. Adem�s de la hip�tesis de la existencia de la corriente de desplazamiento se desprende que si un campo el�ctrico var�a con el tiempo entonces se induce un campo magn�tico. De esta manera, los fen�menos el�ctricos y magn�ticos adquieren una bella simetr�a. Por lo tanto, si de alguna manera en una regi�n del espacio llega a existir un campo, digamos el�ctrico, que var�e con el tiempo, por fuerza tiene que existir simult�neamente el otro campo, en este caso el magn�tico. Los dos campos deben existir al mismo tiempo, es decir, debe existir el campo electromagn�tico. No puede existir un campo que var�e en el tiempo sin la existencia del otro campo. En el caso estacionario, o sea que no depende del tiempo, s� puede existir un campo sin que exista el otro. Por ejemplo, el campo magn�tico producido por un im�n es constante en el tiempo y no lleva un campo el�ctrico.

En segundo lugar, a partir de sus ecuaciones, que incluyen las leyes de Amp�re y de Faraday, encontr� que cada uno de los dos campos, tanto el el�ctrico como el magn�tico, debe satisfacer una ecuaci�n que �result� tener la misma forma matem�tica que la ecuaci�n de onda!, o sea precisamente el tipo de ecuaciones que describen la propagaci�n de ondas mec�nicas como la que se propaga en un cable, en un estanque, en el sonido, etc. (v�ase el cap�tulo XI). Esto significa que si en un instante el campo el�ctrico tiene un valor determinado en un punto del espacio, en otro instante posterior, en otro punto del espacio, el campo el�ctrico adquirir� el mismo valor. Lo mismo ocurre con el campo magn�tico. Por consiguiente, los campos el�ctrico y magn�tico se propagan en el espacio, y como no pueden existir separadamente, el campo electromagn�tico es el que realmente se propaga. Maxwell tambi�n encontr� que sus ecuaciones predec�an el valor de la velocidad con la que se propaga el campo electromagn�tico: �result� ser igual a la velocidad de la luz! Este resultado se obtiene de una combinaci�n de valores de cantidades de origen el�ctrico y magn�tico. Para Maxwell esto no pod�a ser una casualidad y propuso que la onda electromagn�tica era precisamente una onda de luz, o como �l mismo escribi�: "Esta velocidad es tan similar a la de la luz, que parece que tenemos fuertes razones para concluir que la luz es una perturbaci�n electromagn�tica en forma de ondas que se propagan a trav�s del campo electromagn�tico de acuerdo con las leyes del electromagnetismo."

De esta manera, Maxwell contest� la cuesti�n pendiente desde tiempos de Young y Fresnel (v�ase el cap�tulo XIII) sobre qu� es lo que ondula en una onda de luz: es un campo electromagn�tico.

Sin embargo, una vez publicado su trabajo, la comunidad cient�fica lo recibi� con frialdad. Esto se debi�, en primer lugar, a que su teor�a ten�a una presentaci�n matem�tica muy complicada que poca gente de su �poca pudo entender. En segundo lugar, la formulaci�n en t�rminos de campos represent� un cambio revolucionario de las interpretaciones que prevalec�an entonces en t�rminos de acci�n a distancia de la teor�a de Newton. Adem�s, la noci�n de corriente de desplazamiento no se entendi� bien. Finalmente, no hab�a confirmaci�n experimental ni de la existencia de la corriente de desplazamiento ni de las ondas electromagn�ticas. Por lo tanto, no era de extra�ar que pocos f�sicos entendieran el fondo profundo y la importancia de la formulaci�n te�rica de Maxwell. Para esto se hubo que esperar varios a�os; fue ocho a�os despu�s de la muerte de Maxwell que se realiz� la primera confirmaci�n experimental de la existencia de ondas electromagn�ticas, como veremos en el siguiente cap�tulo.