20. Diagrama cartesiano

Corresponde a la sesi�n de GA 2.20 CUADRO ESPACIAL

Los diagramas representan gr�ficamente sucesos o eventos para su mejor compresi�n. En probabilidad, el diagrama cartesiano sirve para identificar todos los posibles resultados de un fen�meno aleatorio con dos variables.

V�ase el ejemplo:

�Cu�les son todas las combinaciones que se pueden hacer con tres jinetes y dos caballos?

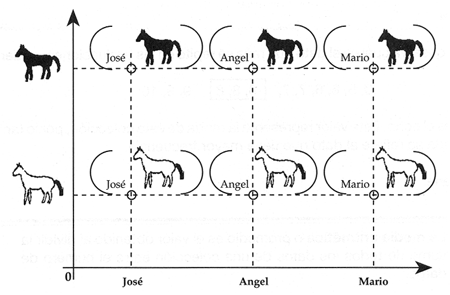
Obs�rvese el diagrama cartesiano en donde los jinetes se definen en el eje de las x y los caballos en el eje de las y.

En el diagrama cartesiano se observa lo siguiente:

a) Aparecen todos los puntos que determinan cada jinete con cada caballo.

b) Cada combinaci�n es una pareja que se denota igual que las coordenadas de un punto; primero la variable del eje de las x y despu�s la variable del eje de las y.

c) El producto del n�mero de jinetes (3) con el n�mero de caballos (2) es igual al total de combinaciones del espacio muestral (6).

Esto es 3 x 2 = 6.

Concluyendo se afirma que:

El diagrama cartesiano es un m�todo de conteo gr�fico mediante el cual se obtiene el espacio muestral de un fen�meno aleatorio con dos variables �nicamente. Cada uno de los puntos que forman la primera y segunda variables representa una de las combinaciones del espacio muestral. El total de resultados es igual al producto del n�mero de lementos de x por el n�mero de elementos de y.