VI. FIGURAS DE ANCHO CONSTANTE
EL CÍRCULO es el lugar geométrico de todos los puntos que equidistan de un punto fijo llamado centro. Es precisamente debido a esta propiedad que las ruedas tienen forma circular. Si ponemos un eje en el centro, al rodar el círculo, debido a que todos los rayos tienen la misma longitud, el eje no sube ni baja, sólo se traslada, siempre a la misma altura sobre el piso.
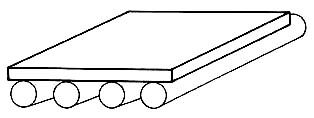
Antes de ser usado como rueda, el círculo tuvo otra aplicación más primitiva, la de ser usado como rodillo. Si colocamos un bloque muy pesado sobre varios rodillos circulares, al rodar éstos, el bloque se traslada sin subir ni bajar, siempre a la misma altura sobre el piso.
Es interesante observar y difícil de creer que estas dos aplicaciones del círculo, rueda y rodillo, están basadas sobre principios radicalmente diferentes, es decir, la propiedad característica del círculo que le permite ser usado como rueda es radicalmente distinta a la propiedad del círculo que le permite ser usado como sección transversal de un rodillo. Tan es así que sólo puede haber ruedas circulares, pero existen rodillos no circulares que, sorprendentemente, funcionan tan bien como los rodillos circulares.
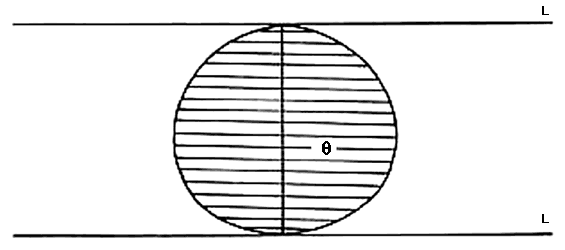
Veamos cuál es la propiedad del círculo que permite que los rodillos circulares funcionen adecuadamente. Esta propiedad no tiene nada que ver con el centro del círculo, lo importante es que el rodillo circular, al rodar, mantiene al bloque siempre a la misma altura sobre el piso, debido a que el ancho del círculo es el mismo en cualquier dirección. Si los rodillos tuviesen forma elíptica, es claro que al rodar éstos, el bloque subiría, bajaría y acabaría finalmente por desequilibrarse y caerse. Esto se debe a que en diferentes direcciones, una elipse tiene diferentes anchos (ver figura VI.2).
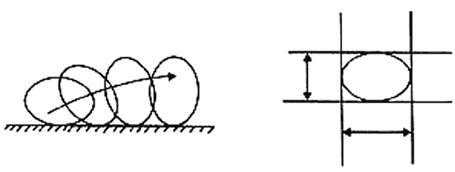
Existen figuras distintas del círculo con la propiedad de que en cualquier dirección que se tomen, su ancho es el mismo y por tanto, usadas como secciones de rodillos, funcionan tan bien como los rodillos circulares.
Veamos primero que significa el ancho de una figura y en una dirección dada. Tomemos una dirección y líneas soporte perpendiculares a está dirección que aprisionen a y. La distancia entre estas dos líneas es el ancho de y en esta dirección (ver figura Vl.3).
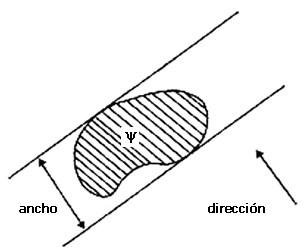
Es claro que si para dos direcciones diferentes el ancho de una figura no es el mismo, entonces esta figura, al ser usada como sección de un rodillo, producirá en el bloque que se pretende trasladar un movimiento hacia arriba y hacia abajo.
Las figuras que tienen el mismo ancho en cualquier dirección son llamadas figuras de ancho constante.
A estas alturas supongo que es urgente conocer una figura de ancho constante distinta del círculo. Quizá la más sencilla sea el triángulo de Reuleaux:
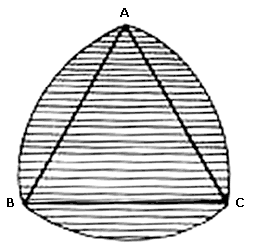
Sea ABC un triángulo equilátero de lado, digamos, uno (es decir, todos los lados del triángulo miden uno). Con centro en A y radio uno tracemos un arco de círculo de B a C (ver figura v.4). Con centro en B y radio uno tracemos un arco de círculo de C a A. Finalmente, con centro en C y radio uno tracemos un arco de circulo de A a B. La figura así obtenida se llama triángulo de Reuleaux.
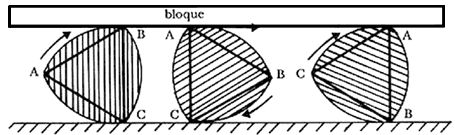
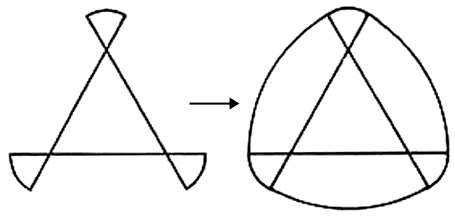
La siguiente serie de dibujos (figura VI.5) nos convencerá de que rodillos cuyas secciones transversales son triángulos de Reuleaux funcionan tan bien como los rodillos circulares. En ellos se muestra a uno de estos triángulos de Reuleaux rodar entre el piso y un bloque de cemento. El triángulo de Reuleaux, al rodar, siempre toca el piso y el bloque. En el primer movimiento el triángulo se apoya en C y el arco AB resbala sobre el bloque, en cambio en el segundo movimiento el arco BC rueda sobre el piso mientras el vértice A se desplaza pegado al bloque.
Lo anterior prueba que el triángulo de Reuleaux es una figura de ancho constante; sin embargo, para reafirmarlo vamos a dar una demostración directa de que el ancho en cualquier dirección es siempre uno:
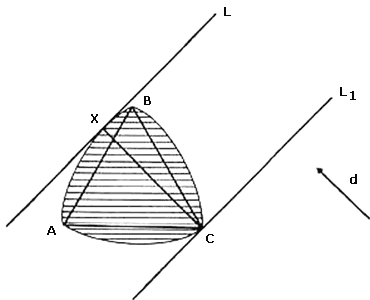
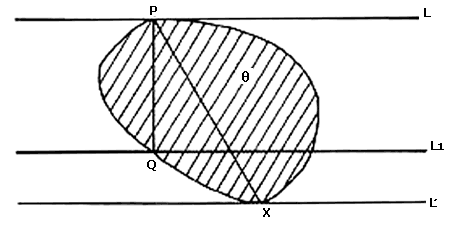
Tomemos una dirección d cualquiera. Es fácil ver que existe una línea L perpendicular a la dirección d que es tangente a alguno de los arcos de círculo que forman el triángulo de Reuleaux. Digamos, por ejemplo, que L es tangente al arco AB en X (ver figura VI.6). La perpendicular a L por X pasa por C, que es el centro del arco AB. Por otro lado, la línea L', paralela a L que pasa por C, es una línea soporte. El ancho del triángulo de Reuleaux en la dirección d está dado por la distancia entre L y L', que es uno, pues es la longitud del segmento CX. Es decir, el ancho en la dirección d es uno y por lo tanto el ancho en cualquier dirección es también uno.
El triángulo de Reuleaux forma parte de un mecanismo muy sencillo que actualmente es usado en la mayoría de los proyectores de cine —es a este mecanismo a quien por cierto le deben su peculiar sonido. Para evitar una imagen borrosa, la película debe correr mientras el objetivo está cerrado y pararse mientras el objetivo está abierto. Para obtener este tipo de movimiento necesitamos un mecanismo que transforme el movimiento circular uniforme en un movimiento que alterne los periodos de descanso con los periodos de movimiento. A continuación describimos este mecanismo.
El mecanismo o aparato consta de dos partes: la primera es una tabla, digamos de madera, en donde existen dos ranuras y una abertura, tal y como lo muestra la siguiente figura VI.7.
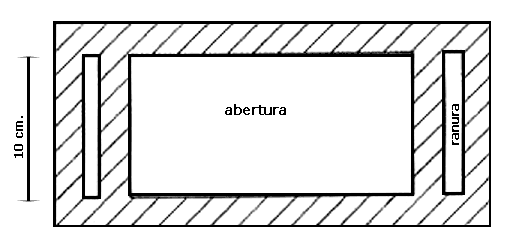
Para fijar ideas, supongamos que el ancho de la abertura es de diez centímetros. Por cada una de las ranuras corre un tornillo pegado, digamos, a la pared, que sólo le permite a la tabla moverse hacia arriba o hacia abajo, pero nunca hacia los lados.
La segunda parte del mecanismo consta de un disco con la forma de un triángulo de Reeuleaux de diez centímetros de ancho, sujeto a un eje por el punto A. El eje trasmite el movimiento circular uniforme, lo que produce que el disco dé vueltas alrededor del eje (ver figuraVI.8).
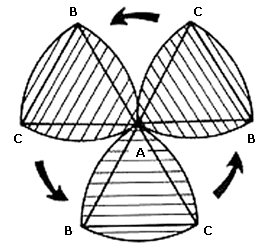
Finalmente, el disco se encuentra encajado dentrode la abertura de la tabla (figura VI.9).
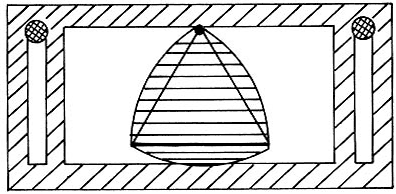
El disco, al girar uniformemente, produce un movimiento —ascendente o descendente— en la tabla, movimiento que describiremos a continuación (ver figura VI.10).
Mientras el disco gira de la posición 1 a la posición 2, el arco BC del disco simplemente se desliza sobre la pared inferior de la abertura sin producir movimiento alguno en la tabla. Por el contrario, mientras el disco gira de la posición 2 a la posición 3, éste empuja a la tabla hasta que alcanza su altura máxima, precisamente en la posición 3. Entre la posición 3 y la posición 4 la tabla permanece en su altura máxima, pues el arco BC del disco simple y sencillamente se desliza sobre la pared superior de la abertura. Finalmente, mientras el disco gira entre la posición 4 y la posición 1, la tabla baja hasta alcanzar su altura mínima en donde permanecerá hasta que el disco pase por la posición 2. De esta manera, el disco gira alrededor del eje A mientras la tabla sube y baja intercalando periodos de reposo cuando alcanza su altura máxima o mínima.
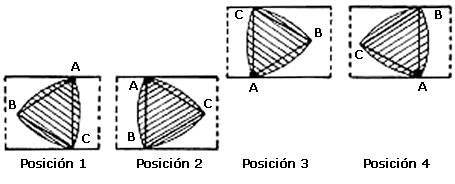
Existen muchas figuras de ancho constante. Por ejemplo, es fácil construirlas sobre polígonos regulares (con número impar de lados):
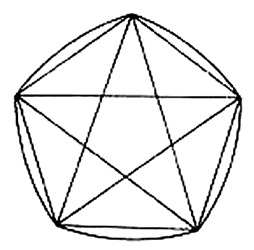
o algunas otras poco simétricas, como la siguiente:
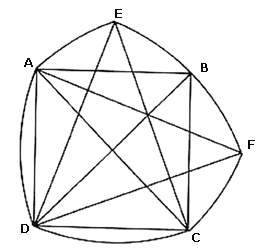
Para trazarla, empecemos por un cuadrado ABCD cuya diagonal tenga longitud, digamos, uno. Sean E y F puntos tales que las distancias ED, EC, FA y FD sean todas uno. Con Centro en D y radio uno tracemos el arco EF que pasa por B. Con centro en C y radio uno tracemos el arco AE. Con centro en A tracemos arco FC y, finalmente, con centros en E y F los arcos DC y AD respectivamente.
Todas las figuras de ancho constante que hemos descrito poseen arcos de círculo, pero es posible construirlas sin que ningún pedacito sea un arco de círculo.
Mencionaremos algunas de las propiedades más interesantes de las figuras de ancho constante.
i) Toda figura de ancho constante uno tiene diámetro uno.
ii) Toda figura de ancho constante uno tiene perímetro p.
iii) Entre las figuras de ancho constante uno, la de más área es el círculo y, la de menor área es el triángulo de Reuleaux.
iv) El incírculo y el circumcírculo de una figura de ancho constante uno son concéntricos y la suma de sus radios es uno.
v) La única figura de ancho constante radicalmente simétrica es el círculo.
Una de las características esenciales de las figuras de ancho constante es que poseen —al igual que los círculos— diámetros. Estos diámetros son aquellos segmentos de la figura con longitud máxima de cuyo comportamiento se desprenden las propiedades principales de una figura de ancho constante. A diferencia del círculo, los diámetros de una figura de ancho constante no concurren siempre en un punto, y cuando así lo hacen es porque la figura o es un círculo o posee un arco de círculo. Para identificar aquellos segmentos con longitud máxima dentro de una figura de ancho constante es preciso empezar viendo qué tan lejanos entre sí pueden estar dos de sus puntos.
La distancia entre cualquier par de puntos de una figura de ancho constante h es siempre menor o igual a h.
Esto se debe simple y sencillamente a que si hubiese dos puntos, X y Y a distancia mayor que h el ancho de la figura en la dirección del segmento XY sería mayor que h, debiendo ser h.
Sí L es una línea soporte de una figura q de ancho constante h, entonces L toca a q en un solo punto.
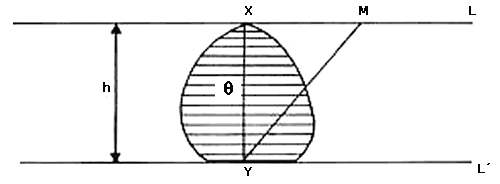
Para ver esto, tomemos L', la línea soporte de q paralela a L (ver figura VI.14). Sabemos que q se encuentra aprisionada en la banda determinada por L y L' y que el ancho de esta banda es h. La línea L' toca a q quizá en muchos puntos, de los cuales vamos a poner nuestra atención sólo en uno de ellos —escójalo usted— al que llamaremos Y. Como la distancia entre L y L' es h existe un solo punto, al que llamaremos X, en L, con la propiedad de que la distancia entre X y Y es h —de hecho, X es el punto de L con la propiedad de que el segmento XY es perpendicular a las líneas L y L'. La distancia entre Y y cualquier otro punto de L, distinto de X, es estrictamente mayor que h. Por lo tanto, como Y está en q, ningún otro punto M de L, distinto de X, puede pertenecer a q —piense también que si M estuviera en q, el ancho de q en la dirección del segmento YM sería mayor que h. Esto nos convence de que L toca a q sólo en el punto X. Esta demostración nos da como regalo, mucho más.
Intercambiando los papeles de L por L' tenemos que L' toca a q solamente en el punto Y y por lo tanto:
Si L y L' son líneas soporte paralelas de una figura q de ancho constante, entonces tanto L como L' tienen conq un solo punto de contacto y el segmento que une estos dos puntos de contacto es perpendicular a L y a L'. (Ver figura VI.5).
Las consecuencias de la proposición anterior son muchas y muy importantes. Las dos más inmediatas son: i) Toda figura de ancho constante es una figura convexa, pues cualquiera de sus líneas soporte la toca en un solo punto. ii) El diámetro de una figura de ancho constante h es h, pues no hay dos puntos a distancia mayor que h, pero existen dos puntos —los de contacto entre dos líneas soporte paralelas— cuya distancia es h.
Llamaremos diámetro de una figura de ancho constante al segmento de línea que une los puntos de contacto de dos líneas soporte paralelas. Por supuesto, debido a que las figuras de ancho constante son convexas, sus diámetros se encuentran contenidos completamente dentro de ellas.
En una figura de ancho constante h, los diámetros son precisamente los segmentos de línea contenidos en la figura que tienen longitud h.
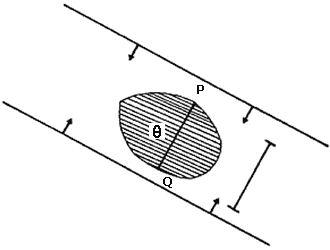
Demostración. En una figura de ancho constante h, la longitud de un diámetro es la distancia entre dos líneas soporte paralelas, que es h. Supongamos ahora que P y Q son dos puntos de una figura q de ancho constante y que la distancia entre ellos es h. Queremos ver que el segmento de línea PQ es un diámetro de q. Si L y L' son las líneas soporte de q perpendiculares al segmento PQ en la banda determinada por ellas, cuyo ancho es h, se encuentra el segmento PQ cuya longitud es también h (ver figura v.16). Es claro entonces que el punto P debe de estar en L y el punto Q en L' —o viceversa— y por tanto que el segmento PQ es un diámetro de q.
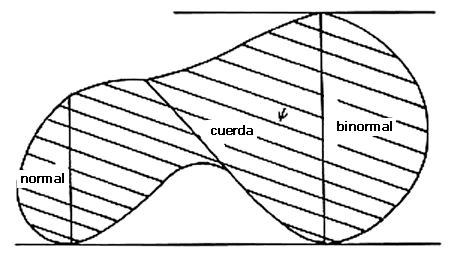
Una cuerda de una figura y es un segmento de línea contenido en y cuyos extremos están en la frontera de y (ver figura VI.l7).
Una normal de una figura y es una cuerda de y con la propiedad de que la línea perpendicular por uno de sus extremos es línea soporte de y. Finalmente, una binormal de una figura y es una cuerda con la propiedad de que las líneas perpendiculares por sus dos extremos son líneas soporte de y (ver figura v.17). Por supuesto, en una figura de ancho constante h, los conceptos de diámetro, binormal y cuerda de longitud h, coinciden.
Es en el siguiente hecho en donde se encuentra la parte más profunda y original de nuestro tratamiento de las binormales de las figuras de ancho constante. Quiero agradecer a Rafael Morales el haberme sugerido parte de su demostración.
Una figura de ancho constante posee una binormal en cada dirección y viceversa; si una figura posee una binormal en cada dirección, es porque la figura es una figura de ancho constante.
Demostración. Supongamos que y es una figura de ancho constante y sea d una dirección cualquiera. Tomemos las dos líneas soporte a y perpendiculares a la dirección d. El segmento que une los puntos de contacto de y con estas dos líneas es una binormal en la dirección d.
Antes de continuar con nuestra demostración, necesitamos la siguiente construcción:
A partir de una figura cualquiera f, vamos a construir otra figura f* de la siguiente manera:
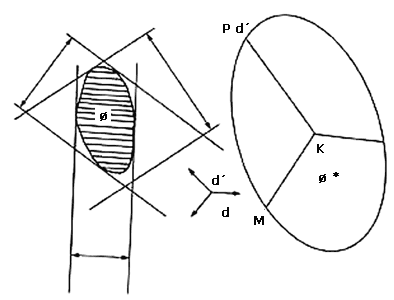
Tomemos un punto fijo K (ver figura VI.18). En la dirección d dibujemos un rayo que empiece en K y sobre este rayo tomemos un punto, al que llamaremos Pd, de tal forma que la distancia entre K y Pd sea precisamente el ancho de f en la dirección d. Al ir variando la dirección d, el punto Pd irá describiendo una figura f* con la propiedad de que si M es un punto en la frontera de f*, entonces la longitud del segmento KM es el ancho de la figura f en la dirección del segmento KM (ver figura VI.19).
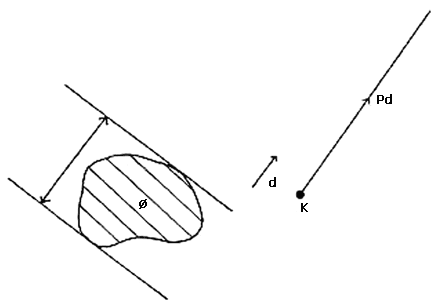
Por supuesto, f* es diferente a f. De hecho, si f es una figura de ancho constante, entonces f* es un círculo, pues el ancho de f es el mismo en cualquier dirección. Por otro lado, si f* es un círculo con centro en K, entonces el ancho de f es el mismo en cualquier dirección, por lo que f es una figura de ancho constante.
Una vez hecha está construcción regresemos a nuestro problema original. Supongamos que la figura y tiene una binormal en cada dirección. Queremos ver que y es una figura de ancho constante.
Para tal efecto bastará ver que y* es un círculo. Para ver que y* es un círculo, vamos a hacer uso del resultado principal del capítulo III, el cual nos dice que si por cada punto frontera M de y* pasa una línea soporte de y* perpendicular a KM, entonces y* es un círculo —y por lo tanto y es una figura de ancho constante.
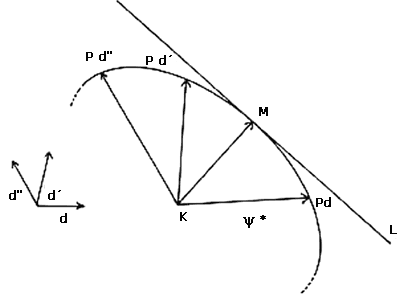
Manos a la obra: Tomemos M, un punto cualquiera de la frontera de y* y sea L la línea que pasa por M y es perpendicular a KM (ver figura VI.20). Queremos probar que L es una línea soporte de y*. Para esto bastará verificar que para cualquier otra dirección d, el segmento KPd nunca cruza la línea L —esto nos asegura que y* está totalmente contenida a un lado de L.
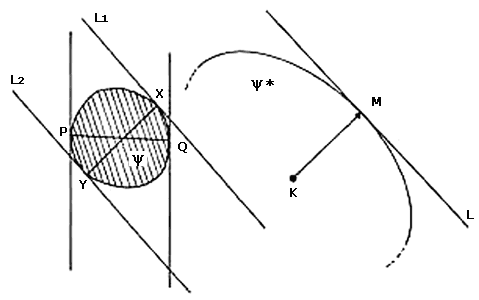
Sean L1 y L2 las dos líneas soporte de y perpendiculares a la dirección KM (ver figura VI.21), y sean X y Y los puntos en los que L1 y L2 tocan a y respectivamente. Sabemos que el segmento XY es paralelo al segmento KM y de igual longitud. Si identificamos a L con L1—que por cierto son paralelas—, es decir, si pintamos a y sobre y* de tal manera que L1 coincida con L y el segmento XY con el segmento KM, veremos que L2 pasa por K y que la figura y se encuentra entre L y L2. Pensemos ahora en d, otra dirección cualquiera (ver figura VI.22). En la dirección d existe una binormal PQ de P cuya longitud es, por supuesto, el ancho de y en la dirección d.
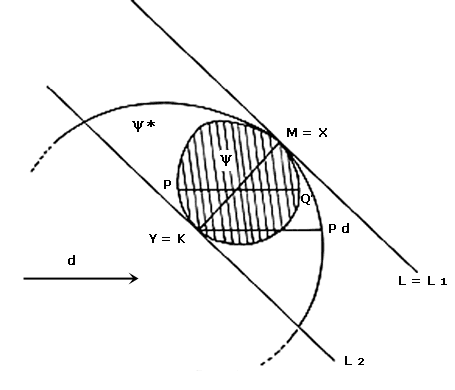
Además, la binormal PQ está contenida en y
y por lo tanto entre L y L2. Como el segmento
PQ y el segmento KPd son paralelos
—pues ambos son paralelos a la dirección d— y de la misma
longitud, es fácil ver que entonces KPd nunca cruza la línea L.
Como esto sucede para cualquier dirección d, la figura y*
nunca cruza la línea L y por lo tanto L —que es perpendicular
a KM por M— es una línea soporte de y*.
Por el resultado principal del capítulo III, y*
es un círculo y por lo tanto y es una figura de ancho constante. ![]()
A continuación enunciaremos algunas propiedades de las binormales o diámetros de una figura de ancho constante h. i) Cualesquiera dos binormales se intersectan en la figura. ii) Si dos binormales se intersectan en un punto frontera, entonces por este punto pasa una multitud de líneas soporte y la parte de la frontera que se encuentra entre los otros dos extremos es un arco de círculo de radio h. iii) Si un segmento de arco de círculo a de radio h' pertenece a la frontera de la figura, entonces h' es menor o igual a h. Si h' es igual a h, el centro de a está en la frontera de la figura y por él pasa una multitud de líneas soporte. Si h' es menor que h, el centro de a está en el interior de la figura y el segmento de arco de radio h-h' concéntrico a a pero diametralmente opuesto, está en la frontera de la figura.
El siguiente resultado clásico es de mucha utilidad.
En una figura de ancho constante toda nornal es binormal y viceversa; si en una figura toda normal es binornal es porque la figura es de ancho constante.
Demostración. Supongamos que q es una figura de ancho constante y que el segmento PQ es una normal de q, es decir, que la línea L perpendicular a PQ por P es línea soporte de q (ver figura VI.23). Queremos verificar que la línea L1 perpendicular a PQ por Q es línea soporte de q. Dibujemos la línea soporte L' de q paralela a L. Sabemos que L' toca a q solamente en un punto, al que llamaremos X, y que el segmento PX es perpendicular tanto a L como a L'. Por lo anterior, el segmento PQ y el segmento PX deben coincidir, el punto X tiene que ser el punto Q y la línea soporte L' tiene que ser la línea L1. Es decir, PQ es una binormal, pues la línea L1, perpendicular a PQ por Q es una línea soporte.
Supongamos ahora que en la figura q toda normal es una binormal. Para convencernos de que q es de ancho constante vamos a construir en cada dirección una binormal.
Sea d una dirección cualquiera. Tracemos una línea soporte L
a q perpendicular a la dirección d
y supongamos que L toca a q —entre
otros— en el punto X. La cuerda de q,
perpendicular a L que empieza en X, es una normal de q
y por lo tanto una binormal que es paralela a la dirección d.
Esto prueba que q posee una binormal en
cada dirección y que por lo tanto es de ancho constante.
![]()
Tomemos una figura F de ancho constante. Sabemos que en cada dirección existe una binormal de F y que todas estas binormales miden exactamente lo mismo, digamos, uno. Vamos a construir una figura, quizá no convexa, de la siguiente manera: por cada binormal 1 de F, tracemos un segmento I' perpendicular a I, de longitud uno, de tal forma que los puntos medios de I y I' coincidan (ver figura VI.24). La binormal I, al ir tomando todas las direcciones, girará sobre la frontera de F y por supuesto, al mismo tiempo, los extremos del segmento I' describirán una nueva curva x. La siguiente figura muestra la construcción anterior para el triángulo de Reuleaux.
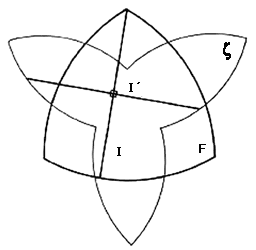
Resulta que la figura x así obtenida es una curva de Zindler, es decir, cada una de las cuerdas I' de x, que por construcción tienen la misma longitud, parten el área y el perímetro de x a la mitad. Recordemos que estas figuras son precisamente aquellas que flotan en equilibrio en cualquier posición, cuando la densidad es un medio.
Por supuesto uno puede revertir el proceso y empezar con una curva de Zindler x, trazando por cada cuerda I' de x que parte el área a la mitad, un segmento I, perpendicular a I' y de la misma longitud, de tal forma que los puntos medios de I y de I' coincidan. Al ir girando I' sobre la curva x, el segmento I describirá una figura de ancho constante F cuyas binormales son las cuerdas I.