BLOQUE 3

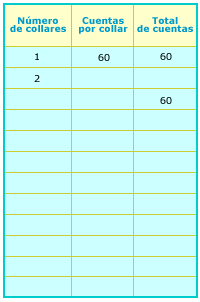
Collares y pulseras Múltiplos y divisores de un número 1. Una artesana que hace collares tiene 60 cuentas y quiere hacer collares iguales sin que le sobren cuentas. ¿Cuántos collares puede hacer y cuántas cuentas llevaría cada collar? Hay varias respuestas correctas, anótalas en la tabla de la izquierda. ¿La artesana puede hacer 18 collares?________ ¿Por qué? _____________________________ _____________________________________ ¿Qué característica común tienen todas las parejas de números que se forman en la primera y segunda columnas?______________________ 2. ¿Cuántas cuentas debería tener la artesana para poder hacer 11 collares con 12 cuentas cada uno?_____________________ Con esa misma cantidad de cuentas hay otros once tipos distintos de collares. Trata de encontrarlos todos y llena la siguiente tabla con tus respuestas. 3. La artesana tiene 12 cuentas rojas y 16 cuentas azules. Quiere hacer pulseras iguales con cuentas de los dos colores, sin que sobren. ¿Cuántas cuentas de cada color puede llevar cada pulsera? ¿Cuántas pulseras se pueden hacer? Hay tres respuestas posibles, trata de encontrarlas y anótalas en la tabla. 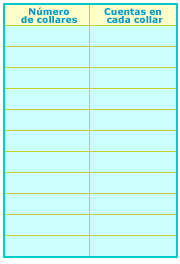¿Se pudieron hacer tres pulseras?______ ¿Por qué?____________________ ___________________________________________________________ ¿Se pudieron hacer 8 pulseras?______¿Por qué? ___________________________________________________________ ¿Cuántas cuentas de cada color lleva la pulsera más chica? _______________ 4. Otro artesano que también hace pulseras tiene 45 cuentas verdes y 60 amarillas. Anota en la tabla los distintos tipos de pulseras que puede hacer. 5. El joven artesano que hace pulseras tiene 27 cuentas rojas, 24 azules y 18 verdes. También quiere hacer pulseras iguales con los tres colores y sin que sobren cuentas. ¿Cuántas cuentas de cada color puede llevar cada pulsera y cuántas pulseras puede hacer? __________________________________________ __________________________________________ Cuando un número divide a otro exactamente se dice que ese número es divisor del otro. Cuando un número divide a otros exactamente, se dice que ese número es divisor común de los otros. Uno, dos, tres y seis, son divisores de seis Tres es divisor común de 27, 24 y 18.