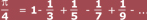Heptágono dividido en 7 triángulos El maestro lee un rollo de papiro a su alumno. Desde la más remota antigüedad, los calculistas se dieron cuenta de que todos los círculos tenían algo en común: su circunferencia y su diámetro estaban siempre en la misma razón. Lo malo es que esta razón no se expresa mediante un número fácil de encontrar porque sólo podemos dar aproximaciones de él. En el siglo xvii, la razón entre la circunferencia y el diámetro fue reconocida como un número, lo que ahora llamamos el número "π" (se lee pi) de periferia, nombre que le daban los griegos a la circunferencia de un círculo. Para los judíos del Antiguo Testamento, 2000 años antes de nuestra era, la circunferencia era el triple del diámetro, el valor de π era entonces 3. En uno de los textos matemáticos más antiguos, el Papiro de Rhind (1700 años a.C.) del Antiguo Egipto, aparece una aproximación para π de ( )2 = , que equivale a 3.16049... Arquímedes, en el año 220 a.C., usó polígonos regulares de hasta 96 lados para aproximar el valor de π entre 3 y 3 . En el año 120 de nuestra era, el matemático chino Chang Hing encontró para π la relación , es decir, 3.15555... En la India, el matemático Aryabhatta, hacia el año 500 de nuestra era, propuso la fracción para aproximar el valor de π. Unos mil años después, aparecieron una multitud de fórmulas que aproximaban cada vez mejor a π. Por ejemplo, el matemático alemán Wilhelm Leibnitz llegó a una fórmula de fracciones con números impares en la que se alternan adiciones y sustracciones: Vista de la Jerusalén bíblica En esta fórmula, entre más sumandos se tomen, mejor será la aproximación de π. En 1949, por primera vez se usó una computadora electrónica para calcular las cifras decimales de π. Se trataba de la ENIAC (por sus siglas en inglés de Computadora e Integradora Numérica Electrónica), de los Laboratorios de Investigación en Balística de los Estados Unidos de América. Con ella se encontraron 2037 cifras decimales de π mediante un cálculo que duró 70 horas. En 1989, los matemáticos de la Universidad de Columbia en Nueva York emplearon una computadora avanzada para encontrar 1 011 196 691 cifras decimales de π. Últimamente, los matemáticos Tamara y Kanada encontraron un método para calcular, por medio de supercomputadoras, los primeros 16 millones de cifras decimales de π. Usa tu calculadora para responder las siguientes preguntas: Computadora ENIAC, 1949 ¿Entre qué valores decimales está la aproximación de π que encontró Arquímedes? ¿Cuál es el valor decimal al que llegó Aryabhatta? Calcula el valor de π con la fórmula de Leibnitz, ¿qué valor obtienes si sólo consideras los 3 primeros sumandos? ¿y si tomas hasta el 5o. sumando?