BLOQUE 4

Relativamente grande o chico La noción de razón en problemas de proporcionalidad 1. Contesta las siguientes preguntas. a) Un producto subió, en un año, 6 pesos. ¿Qué información falta para saber si el aumento fue grande o pequeño? __________________________________ b) El agua de limón se preparó con 10 limones. ¿Qué hace falta para saber si la cantidad de limones fue adecuada? _________________________________ c) Mario faltó tres días a la escuela. ¿Qué hace falta para poder decir si Mario faltó mucho o poco a la escuela? _________________________________________ Con frecuencia, para saber si una cantidad es grande o pequeña, es necesario compararla con otra cantidad. Se dice entonces que la cantidad es relativamente grande o pequeña, en comparación con la otra cantidad. Para saber si las cantidades anteriores (6 pesos, 10 limones, 3 días) son relativamente grandes o pequeñas, faltó información. Anota la información faltante para que esas cantidades resulten relativamente grandes. a) El precio del producto era de __________________________________ b) ________________________________________________________ c) ________________________________________________________ Compara las cantidades que propusiste con las de tus compañeros. 2. La naranjada A se preparó con 5 vasos de agua y 3 vasos de jugo. La naranjada B se preparó con 20 vasos de agua y 8 de jugo. ¿En cuál de las dos naranjadas se usaron más vasos de jugo? _________________________ ¿Cuál de las dos naranjadas sabe más a naranja? _____________________________________ ¿Por qué? __________________________________________________ Compara tus respuestas con las de tus compañeros. El sabor a naranja no depende solamente de la cantidad de vasos de jugo, sino de la relación entre la cantidad de vasos de jugo y la de vasos de agua. Esta relación se llama razón. En la vida cotidiana a veces se le llama "proporción". 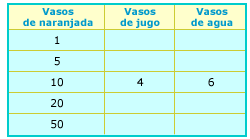Se puede expresar así: "5 vasos de agua por 3 de jugo" Da otro ejemplo en el que una naranjada tenga menos vasos de jugo que otra, y sin embargo sepa más a naranja: Naranjada con más vasos de jugo ________________ Naranjada con menos vasos de jugo ______________ 3. A María le queda muy sabrosa la naranjada. Para preparar 10 vasos de naranjada, usa 4 vasos de jugo. Anota los datos que faltan en la tabla para preparar otras cantidades de naranjada con el mismo sabor que la naranjada de María. Para averiguar qué fracción de 10 vasos de naranjada representan 4 vasos de jugo, completa la siguiente información: 1 vaso es _________________ de 10 vasos. 4 vasos es________________ de 10 vasos. Simplifica la fracción que obtuviste ______________________________ Verifica en tu cuaderno que las otras cuatro cantidades de jugo de la tabla también representan la misma fracción de las cantidades de naranjada. Calcula cuántos vasos de jugo se deben poner por cada 100 vasos de naranjada ________________________________________________ ¿Qué porcentaje de la naranjada corresponde al jugo? _________________________ Con los datos de la tabla anterior, verifica en tu cuaderno que cualquier cantidad de jugo es igual a 40% de la cantidad de naranjada. Una razón o proporción puede expresarse de varias maneras: Mediante dos cantidades"de cada 5 vasos de naranjada, 2 son de jugo". Mediante un número" de la cantidad de naranjada es jugo". Mediante un porcentaje: "40% de la naranjada es jugo". 4. Expresa las razones como se indica.