II. EL FIN DE LOS MITOS
| —Sin duda alguna, Sancho, que ya debemos de llegar a la segunda región del aire, adonde se engendra el granizo, las nieves; los truenos, los relámpagos y los rayos se engendran en la tercera región; y si es que desta manera vamos subiendo, presto daremos en la región del fuego... |
| El ingenioso hidalgo Don Quijote de la Mancha |
LA REVOLUCIÓN DE COPÉRNICO Y SUS CONSECUENCIAS
LA SITUACIÓN empezó a cambiar cuando Copérnico, poco antes de su muerte en 1543, mandó a la imprenta su famoso libro De Revolutionibus, en el que afirmaba que la Tierra y los planetas giran alrededor del Sol. Copérnico pretendía no sólo defender el sistema heliocéntrico, sino también elaborar un modelo para calcular las posiciones de los astros con mayor precisión que Tolomeo. Desgraciadamente, no pudo liberarse de la supuesta perfección del movimiento circular y tuvo que recurrir a los embrollosos epiciclos para poder describir el detalle fino de los movimientos planetarios. Hay que reconocer que si la teoría de Copérnico no fue aceptada de inmediato, se debió en parte a que, para fines prácticos, no era más simple que el sistema de Tolomeo.
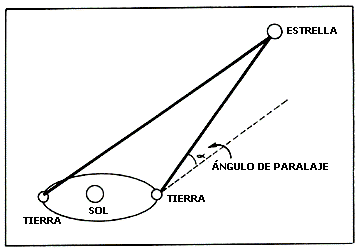
Uno de los argumentos fuertes en contra del sistema de Aristarco y Copérnico era que las estrellas no mostraban ninguna paralaje durante el año terrestre. En efecto, la posición de las estrellas debería de variar por cierto ángulo (la paralaje) durante el recorrido anual de la Tierra alrededor del Sol (Figura 6). Hoy en día sabemos que este efecto existe, pero que es demasiado pequeño para medirse fácilmente. Copérnico argumentó, con justa razón, que la paralaje estelar no puede percibirse porque las estrellas se encuentran demasiado distantes (a distancias que resultaban fabulosas en esa época, ¡Y que eran mucho menores que las reales!). Pero no pudo abandonar la esfera celeste y siguió colocando a las estrellas sobre una bóveda de dimensiones inconcebibles, pero de todos modos finita. Mencionemos también, como dato curioso, que Copérnico rehizo y aceptó sin grandes modificaciones los cálculos de Tolomeo de la distancia Tierra-Sol, valor veinte veces menos que el real. En cuanto a dimensiones, el universo de Copérnico no difería del de los antiguos griegos.
Empero, al privarse a la bóveda estelar de un movimiento real, surgió la posibilidad de que el Universo no tuviera límites. Poco después de la muerte de Copérnico, el inglés Thomas Digges publicó su propia versión del sistema copernicano en el que presentaba al sistema solar rodeado de una distribución infinita de estrellas (Figura 7). Pero el reino de las estrellas de Digges no era semejante a nuestro mundo humano, sino que era la morada de Dios y sus ángeles.
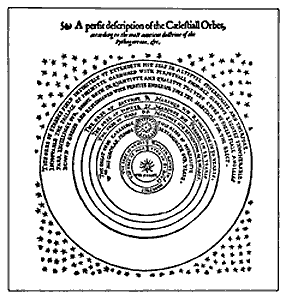
Figura 7. El Universo según Digges (de A Perfit Description of the
Caelestial Orbes, 1576.)
A Giordano Bruno corresponde el mérito de haber concebido un Universo más mundano:
".... existen un número innumerable de soles, y un número infinito de tierras
que giran alrededor de esos soles...", se atrevió a afirmar. Sin embargo, Bruno
llegó a tales conclusiones a partir de especulaciones metafísicas que poco tenían
que ver con un método científico. Su visión del mundo es, en realidad, animista,
y se acerca más al panteísmo que a la ciencia moderna. Y si puso al Sol en el
centro del sistema solar, no fue por razones astronómicas, sino porque le asignaba
a ese astro propiedades vitalistas, al estilo de la filosofía hermética de su
época. De todos modos, las ideas de Bruno le valieron ser acusado de hereje
y morir en una hoguera de la Santa Inquisición justo cuando se iniciaba el siglo
XVII.
Un siglo después de Copérnico, el gran astrónomo Kepler se propuso encontrar las "armonías" que rigen el movimiento de los planetas. Convencido de que el Sol es el centro del Universo, Kepler dedicó largos y penosos años a estudiar los datos observacionales, recopilados por su maestro Tycho Brahe y él mismo, con la esperanza de encontrar algunas leyes simples que rijan con toda precisión el curso de los planetas. Su búsqueda no fue vana; Kepler descubrió las famosas tres leyes que ahora llevan su nombre. De golpe, se desmoronó el embrolloso sistema de epiciclos, del que ni Copérnico había podido liberarse, para dejar lugar a la inesperada simplicidad de las elipses.1
A Kepler le desagradaba la idea de un Universo infinito. Consideraba la cuestión de la finitud o infinitud del mundo como ajeno a la experiencia humana. Pero, además, encontró un argumento para demostrar que el Sol era muy diferente de las estrellas. Antes de que se inventaran los telescopios, se creía que el tamaño aparente de las estrellas correspondía a su tamaño real; se manejaba un valor típico de 2 minutos de arco para el diámetro aparente de una estrella. Kepler demostró que si las estrellas se encontraban tan distantes como lo implicaba el sistema de Copérnico, el diámetro real de una estrella típica debería de ser mayor que la órbita terrestre. Más aún, el cielo visto desde una estrella tendría una apariencia muy distinta de la que se observa desde la Tierra: las estrellas se verían como grandes bolas de luz y no como pequeños puntos luminosos. Hoy en día, sabemos que el tamaño aparente de una estrella es sólo un espejismo producido por la atmósfera terrestre, que ensancha su imagen, pero este fenómeno era desconocido en tiempos de Kepler, por lo que su argumento parecía perfectamente sólido.
El sistema de Copérnico encontró otro gran defensor en un contemporáneo de Kepler: Galileo. Quizás no fue Galileo el primer hombre que miró el cielo a través de un telescopio, pero sí fue el primero en hacerlo sistemáticamente, en interpretar sus observaciones y, sobre todo, en divulgar sus descubrimientos y hacerlos accesibles a un círculo más amplio que el de los eruditos versados en latín. Desde temprano fue Galileo un apasionado defensor de Copérnico y sus observaciones astronómicas vinieron a confirmar sus convicciones. Pero, bajo la presión de los aristótelicos que dominaban la vida cultural de esa época, la Iglesia romana ya había tomado partido por el sistema geocéntrico, por supuestas congruencias con narraciones bíblicas. Galileo se propuso convencer con pruebas objetivas a los altos prelados de la Iglesia de que Copérnico tenía razón; pero después de insistir varios años, sólo obtuvo una prohibición oficial de enseñar el sistema heliocéntrico.
A pesar de todo, Galileo publicó, en 1632, el Diálogo sobre los dos principales sistemas del mundo, libro en el que confrontaba, de una manera supuestamente imparcial, las doctrinas de Aristóteles y de Copérnico. Pero nadie podía engañarse con las simpatías del autor: el héroe del libro era Salviati, defensor de Copérnico, quien refutaba uno por uno los argumentos de su contrincante, el filósofo peripatético Simplicio, torpe defensor de Aristóteles. El Diálogo fue escrito originalmente en italiano y pretendía ser un libro de divulgación más que un texto científico. Del sistema de Copérnico, sólo aparecía la idea heliocéntrica, sin los embrollos matemáticos de la teoría. No todos los argumentos de Galileo eran claros, o aun verdaderos: al final del libro, por ejemplo, aparece una teoría de las mareas, totalmente errónea, con la cual pretendía demostrar el movimiento de la Tierra. Más aún, no se menciona en el libro ni media palabra de los descubrimientos de Kepler, que Galileo no pudo valorar correctamente. Pero a pesar de sus limitaciones, el Diálogo tuvo el efecto suficiente para causar revuelo en el medio científico y religioso. Apenas publicado, fue vetado por la Iglesia, y Galileo fue juzgado y condenado a retractarse de sus convicciones.2
Por lo que respecta a la cosmología, Galileo descubrió que la Vía Láctea está compuesta por una infinitud de pequeñas estrellas que sólo pueden distinguirse con un telescopio. Así se aclaraba el misterio de esa banda luminosa en el cielo que tanto había despertado la imaginación de los filósofos y los poetas.
También descubrió Galileo que el telescopio reducía el tamaño aparente de las estrellas. Sospechó que tal tamaño era una ilusión óptica y la achacó al mecanismo de visión del ojo. Sin embargo, siguió pensando que el diámetro aparente no era totalmente ilusorio y le adscribió un valor promedio de 5 segundos a una estrella de primera magnitud y 5/6 de segundos a una de sexta. A partir de ahí, Galileo calculó que una estrella de sexta magnitud debía de encontrarse a 2 160 unidades astronómicas.3 Aunque todavía erróneo, este valor permitía considerar seriamente que las estrellas son semejantes a nuestro Sol.
En cuanto al tamaño del Universo, Galileo se mostró excepcionalmente cauto al respecto. "Es aún incierto (y creo que lo será siempre para la ciencia humana) si el mundo es finito o, lo contrario, infinito..." llegó a afirmar,4 y con cierta razón, pues cualquier otra posición basada en los conocimientos de su época hubiera sido simple especulación.
Las observaciones de Galileo permitieron alejar suficientemente a las estrellas
para que no pareciera descabellado afirmar que el Sol es una estrella común,
cuya única particularidad es estar muy cerca de nosotros. A Christian Huygens
(1629-1695) corresponde el primer intento de medir la distancia a las estrellas.
Suponiendo que la estrella Sirio es igual al Sol, Huygens trató de comparar
el brillo de estos dos astros para determinar sus distancias relativas. Para
ello hizo pasar la luz del Sol a través de unos pequeñísimos agujeros, hasta
que la cantidad de luz solar que quedaba le pareciera comparable a la luz de
Sirio. Conociendo el tamaño de los agujeros, calculó que si el diámetro solar
fuese 27 664 menor de lo que es, el Sol se vería con el mismo brillo que Sirio.
Por lo tanto, esta estrella debería encontrarse 27 664 veces más alejada de
la Tierra que el Sol. Y Huygens no dejó de admirarse de tan fabulosa distancia:
| una bala de cañón tardaría cientos de miles de años en llegar a las estrellas... y sin embargo, cuando las vemos en una noche clara, nos imaginamos que se encuentran a no más de unas cuantas millas encima de nuestras cabezas... y que número tan prodigioso de estrellas debe haber aparte de éstas, tan remotas de nosotros...5 |
No se imaginó Huygens que la distancia que calculó era veinte veces menor que la real, y que ésta a su vez es un modestísimo intervalo, casi humano, en la escala cósmica.
La manera correcta de calcular las distancias relativas del Sol y las estrellas (suponiendo que todas tienen el mismo brillo real) es comparar directamente sus brillos aparentes. Una ley simple y fundamental de la óptica es que la luminosidad aparente de un objeto disminuye como el cuadrado de su distancia: así, por ejemplo, un foco colocado a 20 metros se ve 4 veces menos brillante que si estuviera a 10 metros, a 80 metros se ve 9 veces menos brillante, etc. Debido a la gran disparidad entre el brillo del Sol y el de cualquier estrella, es imposible compararlas con suficiente precisión. En 1668, el matemático escocés James Gregory tuvo la idea de comparar una estrella con Júpiter, cuyo brillo relativo con respecto al Sol puede calcularse indirectamente a partir de la distancia y la reflectividad de este planeta. El método es esencialmente correcto (a diferencia del de Huygens) y Gregory encontró que Sirio se encuentra a 83 190 unidades astronómicas.
Hasta tiempos de Galileo, y aun después, no se había percibido ninguna relación entre la caída de los cuerpos en la Tierra y el movimiento de los planetas en el cielo. Nadie había refutado la doctrina de Aristóteles de que los fenómenos terrestres y los celestes son de naturaleza totalmente distinta, y que los sucesos más allá de la órbita lunar no pueden entenderse con base en nuestras experiencias mundanas.
La situación cambió drásticamente cuando Isaac Newton descubrió que la gravitación es un fenómeno universal. Todos los cuerpos en el Universo —ya sean manzanas, planetas o estrellas— se atraen entre sí gravitacionalmente; y la fuerza de atracción (F) entre dos cuerpos es proporcional a sus masas (M1 y M2) e inversamente proporcional al cuadrado de la distancia (D) que los separa:
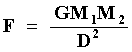
donde G es la constante de la gravitación.
Según una leyenda muy conocida, Newton llegó a tales conclusiones un día que, sentado bajo un manzano y meditando sobre el por qué la Luna se mantiene unida a la Tierra, vio caer una manzana. La realidad es más complicada: Newton encontró la clave del sistema del mundo en las leyes de Kepler. Guiado por ellas, logró demostrar que el movimiento de los planetas es producido por la atracción gravitacional del Sol sobre ellos. Para tal hazaña intelectual, que ocurrió en los años 1684-1685, Newton utilizó un poderosísimo método matemático que él mismo había inventado en su juventud.6 Sus resultados los publicó en 1686 en el célebre libro llamado los Principia, que señala el nacimiento de la física como ciencia exacta.
El problema del movimiento de los planetas había sido resuelto finalmente, pero quedaban las estrellas. Inspirado seguramente por el método de Gregory, Newton hizo un cálculo simple7 para demostrar que el Sol se vería del mismo brillo que Saturno si estuviera 60 000 veces más alejado (suponiendo que este planeta refleja una cuarta parte de la luz solar). Este valor equivale a unas 600 000 unidades astrónomicas, que sería la distancia típica a una estrella de primera magnitud, en perfecto acuerdo con los conocimientos modernos (Sirio, por ejemplo, se encuentra a 550 000 unidades astronómicas). Así, en tiempos de Newton ya se tenía plena conciencia de las distancias interestelares. También son de esa época los primeros intentos de calcular la distancia de la Tierra al Sol, midiendo la paralaje del Sol visto desde dos lugares alejados de la Tierra; los resultados obtenidos no eran demasiado erróneos.8
La existencia de la gravitación universal implica que las estrellas deben estar, efectivamente, muy alejadas para no influir sobre el Sol y sus planetas. Pero, aun infinitesimal, esa atracción no puede ser totalmente nula: un conglomerado de estrellas acabaría por colapsarse sobre sí mismo debido a la atracción entre sus partes, y ése sería el destino de un Universo finito. Newton llegó a la conclusión de que, para que ello no suceda, el Universo debe ser infinito y uniforme; sólo pequeñas regiones pueden colapsarse sobre sí mismas para formar regiones más densas —y es quizás así como se forman las estrellas, especuló el gran científico inglés.
Con el surgimiento de la física newtoniana quedó liquidada definitivamente la física aristotélica, con sus esferas celestes y regiones empíreas. No quedaba duda: nuestro sistema solar es apenas un punto en el espacio y las estrellas son las verdaderas componentes del Universo.
Desgraciadamente, un Universo infinito no estaba excento de problemas. Prueba de ello es una famosa paradoja que se atribuye a Wilhelm Olbers, quien la publicó en 1823, y que intrigó a los cosmólogos durante más de un siglo. El problema fue señalado por primera vez por el astrónomo inglés Halley —contemporáneo de Newton— y consiste en el hecho de que el cielo debería ser infinitamente brillante si el Universo fuera infinito.
Supongamos que dividimos el Universo en una serie de cáscaras esféricas de igual grosor y con centro en el Sistema Solar, tal como se ve en la (figura 8.) Si la distribución de estrellas es uniforme, el número de estrellas en una cáscara dada es proporcional al volumen de la misma, y este volumen es proporcional al cuadrado del radio de la cáscara. Por otra parte, las estrellas en esa cáscara se verían desde la Tierra con una luminosidad inversamente proporcional al cuadrado de la distancia a la que se encuentran, o sea, el radio de la cáscara. En consecuencia, el brillo de cada cáscara es el mismo, independientemente de su radio: en cáscaras cada vez más lejanas, la disminución del brillo de cada estrella se compensa exactamente por el aumento en el número de estrellas en cada cáscara. Si el Universo es infinito, el número de cáscaras esféricas en que lo podemos dividir es infinito. El brillo de cada cáscara puede ser muy pequeño, pero una cantidad pequeña sumada un número infinito de veces da una cantidad infinita. Como consecuencia, el brillo sumado de todas las estrellas debería ser infinito, en contradicción con el cielo negro y estrellado que vemos de noche.
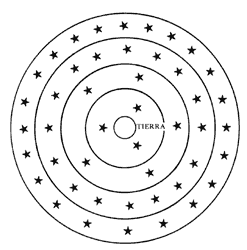
Figura 8. Paradoja de Olbers: si se divide el Universo en cáscaras concéntricas,
de igual grosor y centradas en la Tierra, el brillo de cada cáscara es el mismo,
y el brillo de todas las cáscaras sumadas es infinito.
Los astrónomos partidarios de un Universo infinito propusieron diversas soluciones
al problema. La más simple era suponer que el espacio interestelar no es totalmente
transparente, sino que contiene materia muy difusa que absorbe parte de la luz.
Se pudo demostrar que aun una pequeñísima absorción era suficiente para volver
al cielo oscuro. El único inconveniente de esta solución era que, todavía a
principios del siglo XX, no se había descubierto ninguna prueba observacional
de que el espacio cósmico no es completamente vacío.
Un siglo después de Newton, el filósofo alemán Immanuel Kant (1724-1804) decidió examinar el problema de la extensión del Universo desde el punto de vista de la filosofía. Reunió todos los argumentos en favor y en contra de un Universo sin límites y mostró que era posible, a partir de razonamientos puramente lógicos, demostrar tanto la finitud como la infinitud del Universo (la llamada antinomia de extensión9). Para Kant, la contradicción residía en nuestro sistema cognoscitivo, ya que existían limitaciones naturales a nuestras posibilidades de comprender el Universo.
Como lo sugiere su nombre, la Vía Láctea es una franja luminosa, y su aspecto debe corresponder a la forma del Universo estelar. Alrededor de 1750, un caballero inglés llamado Thomas Wright propuso un ingenioso modelo del Universo, según el cual, las estrellas estaban distribuidas más o menos uniformemente en un plano infinito en el que se encontraba inmerso el Sol. Al mirar en una dirección perpendicular el plano, se ven sólo las estrellas más cercanas, pero en la dirección del plano se observan una infinitud de estrellas distribuidas en una franja que rodea la bóveda celeste. Ésta es justamente la apariencia de la Vía Láctea en el cielo nocturno (Figura 9).
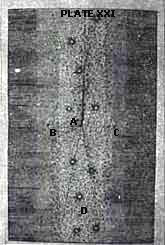
Figura 9. Modelo de la Vía Láctea, según Thomas Wright: el Sol se encuentra
en el punto A. Este diagrama apareció en su libro Una teoría original o nueva
hipótesis del Universo, 1750.
Por una ironía de la historia, las especulaciones filosóficas de Kant sobre
el Universo se volvieron obsoletas a medida que avanzaba la ciencia;10
pero otras especulaciones suyas sobre cosmogonía, publicadas en una de sus obras
de juventud,11 habrían de volverse inmortales. Kant conocía
el modelo de Wright del Universo planar y la teoría de la gravitación universal
de Newton, y se dio cuenta de que eran incompatibles. El problema fundamental
era mantener la estructura de la Vía Láctea sin que se colapsara sobre sí misma.
Kant encontró la clave del problema en el Sistema Solar: los planetas son atraídos
por el Sol, pero no caen sobre éste debido a que giran a su alrededor y la fuerza
centrífuga compensa la atracción gravitacional. Del mismo modo, la Vía Láctea
podría mantenerse estable si las estrellas estuvieran distribuidas, no en un
plano infinito, sino en un disco en rotación. Las estrellas todas describirían
gigantescas órbitas alrededor del centro de la Vía Láctea y su fuerza centrífuga
impediría el colapso.
No contento con una hipótesis tan audaz, Kant dio un segundo paso aún más espectacular. Si la Vía Láctea es un conglomerado de millones de estrellas con forma de disco, ¿no podrían existir otras Vías Lácteas, semejantes a la nuestra y tan lejanas de ella como las estrellas lo son de los planetas? Tales conglomerados se verían como simples manchas luminosas debido a sus enormes distancias y sus formas serían circulares o elípticas. Y justamente tales objetos ya habían sido observados, señaló Kant: son las llamadas estrellas nebulosas, o al menos una clase de ellas: manchas luminosas sólo visibles con un telescopio y cuya naturaleza era un misterio en su época.
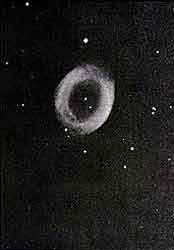
El gran astrónomo William Herschel (1738-1822) llegó a conclusiones parecidas, pero a partir de observaciones directas. Herschel construyó lo que fue el mayor telescopio de su época, y con él estudió la configuración de la Vía Láctea. Suponiendo que la extensión de una región sideral es proporcional al número de estrellas que se ven en ella, Herschel concluyó que nuestro sistema estelar tiene una forma aplanada, de contornos irregulares (parecida a una amiba, Figura 10), y con el Sol en la región central. También descubrió Herschel numerosas nebulosas y se preguntó, al igual que Kant, si no serían lejanísimos conglomerados de estrellas. Tal parece que ésa fue su opinión, hasta que un día descubrió una nebulosa con forma de anillo y una estrella situada muy conspicuamente en su centro, asociada sin ninguna duda a la nebulosa (Figura 11); ésta no podía ser un "universo-isla", sino materia circundante de la estrella.

Figura 10. La forma de la Vía Láctea, según William Herschel; el Sol se
encuentra en el centro. (En The Collected Works of Sir William Herschel,
Londres 1912.)
En el siglo XIX, el astrónomo inglés Rosse construyó un telescopio
aún más potente que el usado por Herschel y estudió detalladamente las nebulosas.
Se dio cuenta de que presentaban formas diversas; algunas, en particular,
tenían brazos espirales y recordaban rehiletes.
Los astrónomos empezaban a sospechar que bajo el nombre genérico de nebulosas habían agrupado objetos muy distintos entre sí. ¿Son algunas nebulosas "universos-islas"? ¿Y qué son las otras? La incógnita habría de perdurar todavía un siglo después de la muerte de Kant y Herschel.
NOTAS
1 Recordemos brevemente las tres leyes keplerianas. 1) Los planetas se mueven en elipses con el Sol en un foco. 2) El radio vector del Sol a un planeta barre áreas iguales en tiempos iguales. 3) El cuadrado del periodo orbital de los planetas es proporcional al cubo de sus radios orbitales.
2 A Galileo se le presenta comúnmente como un mártir de la lucha entre la verdad y el oscurantismo religioso. En Los sonámbulos, Arthur Koestler sostiene una posición distinta: según él, el juicio fue el resultado de una sucesión de malentendidos, causados en parte por la vanidad de Galileo. Me parece que Koestler subestimó el papel de Galileo como uno de los fundadores de la nueva ciencia, dando demasiada importancia a sus equivocaciones, que las tuvo como todo científico, y sus pendencias con la comunidad académica de su época.
3 Unidad astronómica: distancia de la Tierra al Sol (aproximadamente 150 millones de kilómetros).
4 Carta a Ingoli (Opere, vol. VI, p, 518), citada por A. Koyré, Del mundo cerrado al Universo infinito.
5 C. Huygen, Cosmotheoros; citado en Theories of the Universe, M. K. Munitz ed. (Free Press, Illinois, 1957).
6 También inventado independientemente y casi al mismo tiempo por Leibniz, afrenta que Newton nunca le perdonó.
7 Artículo 57 del Sistema del mundo, IV parte de los Principia.
8 La primera medición suficientemente precisa de la distancia Tierra-Sol fue realizada por el astrónomo alemán Encke en 1824.
9 I. Kant, Crítica de la razón pura. 10 Kant no se había imaginado que el espacio no es euclidiano, como veremos en el capítulo IV. Véase también J.J. Callahan, "The Curvature of Space in a Finite Universe", Scientific American, p. 20, agosto de 1976. 11 Historia natural y universal y teoría de los cielos (1755). El pasaje en cuestión se encuentra en Munitz, op. cit., p. 225