XVI. PLANCK Y LA CATÁSTROFE ULTRAVIOLETA

EN EL breve recuento que hicimos de la mecánica estadística sugerimos, tal vez, la idea de que los subsistemas eran siempre partículas en movimiento. Ésta es una inferencia errónea, pues los métodos de la mecánica estadística son más generales. Se pueden aplicar, por ejemplo, a las ondas electromagnéticas que oscilan en el interior de una cavidad, como aquella que imaginó Kirchhoff al tratar la radiación del cuerpo negro. Éste es también un sistema termodinámico, susceptible de análisis con las técnicas estadísticas. La conclusión de este análisis fue ñla existencia del cuanto!

Herman Helmholtz (1821-1894), Rudolf Clausius (1822-1888) y Gustav Kirchhoff (1824-1887) tuvieron muchas cosas en común. Además de ser físicos alemanes contemporáneos y de haber hecho contribuciones fundamentales a la termodinámica —a Helmholtz debemos la primera ley, a Clausius la segunda y de las hazañas de Kirchhoff ya hemos hablado—, los tres fueron profesores de la Universidad de Berlín y ahí dejaron una gran tradición, que habrían de heredar dos de sus alumnos, Wien y Planck.

El primero de ellos, Wien, obtuvo su doctorado con Helmholtz y poco después empezó a trabajar en el problema de la radiación del cuerpo negro. Observándola encontró que las longitudes de onda de la radiación electromagnética emitida se distribuyen de una manera que no es uniforme, sino que su intensidad presenta un pico en un valor intermedio, como se muestra en la Figura 17.

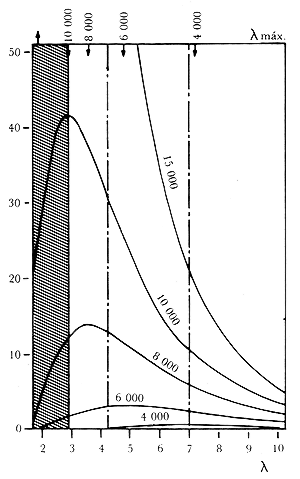
Figura 17. Intensidad de la radiación electromagnética emitida por un cuerpo negro. Se observa un pico en la intensidad para una longitud de onda intermedia.

La longitud de onda en el pico de la curva varía inversamente con la temperatura, de tal forma que a medida que ésta aumenta el color predominante se corre hacia el azul. A esta propiedad se le llama la ley del desplazamiento de Wien, quien pudo deducirla con puro razonamiento termodinámico. Para ello supuso que en la cavidad del cuerpo negro existe un conjunto de ondas electromagnéticas que ejercen presión sobre las paredes de esa cavidad. Con este mismo modelo, lord Rayleigh pudo explicar la forma de la curva en la figura para frecuencias pequeñas; Wien mismo lo hizo cuando esas frecuencias son grandes, aunque ninguno de los dos pudo obtener de la mecánica estadística la forma completa de la curva. El cálculo de Rayleigh, correcto según los cánones de la física clásica, predecía una intensidad que siempre crecía con la frecuencia, como el cuadrado de ésta. En consecuencia, la energía total radiada es infinita y nos hallamos frente a una verdadera catástrofe ultravioleta.

Aunque primero realizó estudios sobre la física y la música, pronto Planck siguió la tradición establecida en Berlín por sus ilustres maestros y se dedicó a analizar problemas termodinámicos. Emplea el mismo modelo que lord Rayleigh y elige un simple oscilador armónico cargado (es decir, una carga que oscila sujeta a un resorte) para simular la emisión de luz. Con ello deduce de inmediato que la intensidad emitida a una cierta frecuencia se determina por dos factores: el primero, proporcional al cuadrado de la frecuencia, y el segundo, a la energía promedio contenida en el oscilador. El primer factor es equivalente a la ley de Rayleigh; el segundo, la energía promedio, es proporcional a la temperatura absoluta de la cavidad y la constante de proporcionalidad es, de acuerdo con un teorema general que Boltzmann probó en la mecánica estadística clásica, una constante universal k, que hoy llamamos la constante de Boltzmann. Con ello Planck obtiene un resultado acorde con la ley de Wien y con la catástrofe ultravioleta. Estas conclusiones de la mecánica y el electromagnetismo clásicos son inevitables.

Para eliminar esa catástrofe, Planck se vio forzado a una medida extrema y audaz. Al calcular la energía promedio en cada oscilador, abandonó las recetas de Boltzmann y postuló que las energías del oscilador sólo vienen en paquetes, que él denominó cuantos. La energía sólo puede ser múltiplo de una energía fundamental, ₀, que es la de un paquete. Con esta suposición tan revolucionaria, Planck pudo explicar los resultados de la Figura 17, eliminando así la catástrofe ultravioleta. Al mismo tiempo, cerró el capítulo clásico de la física y abrió el que dominaría a esta ciencia durante el siglo XX: el capítulo de la física cuántica.