XXIV. EL MONOPOLO MAGNÉTICO DE DIRAC

A PESAR de que el electromagnetismo clásico funciona muy bien bajo la suposición de que no hay monopolos magnéticos, nada hay en la física clásica que prohiba su existencia. ¿Será esto cierto en la física cuántica o habrá en ella algún obstáculo para el monopolo? Ésta es la pregunta que Paul Dirac se planteó en 1931 y a la que dio una respuesta por demás ingeniosa. Dirac halló algo más, pues demostró que de existir una carga magnética aislada, se encontraría la respuesta a una vieja incógnita de la física moderna: ¿por qué todas las partículas elementales que podemos observar aisladas tienen una carga que es múltiplo entero de la del electrón?

El razonamiento de Dirac, en su más pura usanza, es un claro ejemplo del pensamiento matemático aplicado a la física. Es una manifestación clara, también, de la creencia de Dirac según la cual incluso es mejor tener belleza en las ecuaciones de la física que ajustar los datos experimentales. No obstante, puede omitirse lo que sigue y, sin perder continuidad en la lectura, pasar directamente al siguiente capítulo.

Todo arranca de la interpretación de la función de onda de Schrñdinger que, como postuló Born, al elevarse al cuadrado es proporcional a la probabilidad de encontrar a la partícula, digamos a un electrón. Ahora bien, la ecuación de Schrñdinger admite soluciones que en general son números complejos, por lo que ese cuadrado debe entenderse como el valor absoluto de la función de onda y al cuadrado. Esto implica que una función de onda cualquiera y otra que se obtenga multiplicándola por una función cuyo valor absoluto valga uno tienen la misma información física. Tan buena es una como la otra.

A estas funciones de valor absoluto unidad los físicos y matemáticos las llaman fases. Estas fases pueden o no depender del punto del espacio-tiempo. Si no dependen, nada espectacular ocurre. Pero si existe alguna dependencia espacio-temporal de la fase, pueden también ocurrir dos cosas: al recorrer un circuito cerrado en el espacio, la fase puede o no recuperar su valor. Si lo recupera, nada espectacular ocurre, pero si la fase no regresa al valor que tenía antes del recorrido por el circuito y al llegar al mismo punto, Dirac dice que ello significa que el electrón está sujeto a un campo electromagnético.

En este sentido, Dirac encuentra un segundo principio de equivalencia en la física. El primero, postulado por Einstein, nos dice que un sistema de referencia acelerado (como un elevador que cae, por ejemplo) es indistinguible de un campo gravitacional constante. Dirac nos dice que estas fases raras que no regresan a su valor al recorrer un circuito son indistinguibles de un campo electromagnético.

Y continúa Dirac su razonamiento impecable: la fase es una función matemática peculiar, pues al aumentarse por un múltiplo entero del número 2p nada pasa. Por ello el cambio en la fase, al recorrer el circuito, o este cambio más 2np siendo n un número entero, da lo mismo. Por su principio de equivalencia, éste es el flujo magnético, o sea, la cantidad de líneas de campo magnético que cruzan cualquier superficie S que bordee al circuito. Cuando este circuito es muy pequeño, el flujo magnético y el cambio en la fase se anulan, por lo que n debe ser igual a cero. Todo está de acuerdo a nuestros prejuicios.

Sin embargo, hay algunos puntos donde y es cero. En tal caso, por pequeño que sea el circuito, la fase puede cambiarse bruscamente y ya no se anularía necesariamente. En general, y = 0 a lo largo de una línea en el espacio, que llamaremos línea nodal. Pueden darse dos situaciones distintas: la línea nodal tiene o no un principio. En el primer caso, surge algo interesante, como ahora veremos.

Supongamos que la superficie S que rodea al circuito se cierra, esto es, que hacemos el circuito pequeñísimo. Ya que una superficie cerrada no tiene perímetro, el cambio en la fase al recorrer ese perímetro se anula. Sólo sobreviven las líneas nodales, donde y es igual a cero. Si la línea nodal no tiene principio ni final, nada ocurre, pues esa línea contribuye dos veces al flujo magnético en S: de manera positiva cuando entra a la superficie, de forma negativa cuando sale. Pero si la línea nodal empieza (o termina) dentro de S, ñun campo magnético se origina ahí adentro! Es como si hubiera una carga magnética, como si existiera el monopolo. Nada hay en la mecánica cuántica que impida la presencia del monopolo.

Llegamos así, tomados de la mano de Dirac, a la situación siguiente: existen algunas funciones de onda de Schrñdinger con una línea nodal que tiene un principio o un final. En estos puntos en que comienza o termina la línea nodal se encuentra un monopolo magnético, que produce unas líneas de campo magnético semejantes a las de la Figura 13a. Si las líneas empiezan en ese punto, por convención llamamos al monopolo "norte", y si ahí acaban le llamamos "sur".

Dirac aplica después las leyes del electromagnetismo —las ecuaciones de Maxwell— al problema de un electrón con carga e que se mueve frente a un monopolo de intensidad m. Si m ha de existir, la mecánica cuántica requiere que

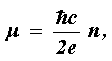
donde n es un entero o, puesto al revés, la carga eléctrica ha de ser un múltiplo entero de la cantidad c/2m. Si en algún punto del universo existiera un monopolo magnético, la carga eléctrica sería por fuerza un múltiplo entero de una carga eléctrica fundamental. A esto le llaman los físicos la cuantización de la carga. El monopolo de Dirac es la única explicación razonable que tenemos de este hecho misterioso. De ahí la importancia que sus colegas dieron a esta idea revolucionaria.