XXIII. A MANERA DE RESUMEN
EL ESTUDIO de cargas eléctricas en reposo y en movimiento uniforme nos indujo a considerar dos tipos de campos de fuerza, los eléctricos y los magnéticos. Si suponemos que el principio de relatividad de Einstein, la invariancia de carga y la ley de Coulomb son válidos, podemos entender el origen relativista de las fuerzas magnéticas. El campo magnético se produce porque las distancias se contraen cuando se las observa en movimiento y ello causa un desequilibrio entre las densidades de carga positiva y carga negativa dentro de un alambre, según las ve un observador (una carga) en movimiento. En pocas palabras, y contrariamente a lo que ocurre con la fuerza eléctrica, el origen del campo magnético no se debe a la existencia de polos magnéticos: en la electrodinámica clásica el monopolo magnético no es necesario, aunque nada prohibe su existencia.
La ley de Gauss (o la de Coulomb) nos dice el campo eléctrico que genera un conjunto de cargas eléctricas; la ley de Ampère modificada con la corriente de desplazamiento nos indica que las cargas en movimiento y los campos eléctricos variables en el tiempo producen un campo magnético y la ley de Faraday, a su vez, muestra cómo un campo magnético que varía en el tiempo induce un campo eléctrico. Si a estas tres leyes agregamos la inexistencia del monopolo magnético, tenemos las cuatro ecuaciones de Maxwell, base de la teoría electromagnética clásica.
Ya escribimos, por el mero placer de mostrar la belleza de las matemáticas,
estas cuatro ecuaciones en la Figura 15, donde usamos el lenguaje del cálculo
vectorial. Es posible escribirlas también en la notación de la relatividad especial,
notación con la cual las cuatro ecuaciones se convierten en un par de relaciones
y resalta aun más su asimetría. Los símbolos Fmn,
y F+mn, que se ven en la Figura
21, designan las varias componentes de los campos eléctricos y magnéticos y
el símbolo 
denota
la operación matemática que permite ver cómo cambian F y F+ con las
coordenadas espaciales y el tiempo. Por otro lado, jm
está ligada a la corriente y a la densidad de carga eléctricas. Un término equivalente
a éste no existe en la segunda ecuación. Por ello las ecuaciones no son simétricas:
una tiene un lado derecho diferente de cero, en la otra el lado derecho es nulo.
Si el monopolo magnético existiera, este último cero debería reemplazarse por
un atérmino para representar a la corriente magnética.
 |
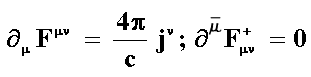Las ecuaciones de Maxwell serían totalmente simétricas, también, donde jm fuera cero, es decir, donde las cargas y corrientes eléctricas no existieran. Por definición misma del vacío (clásico), esto ocurre ahí. Las ecuaciones predicen que una onda electromagnética puede transmitirse en el vacío: sin necesidad de un medio material que los sustente, los campos eléctricos y magnéticos que varían en el tiempo se mantienen uno al otro. De aquí surge la teoría electromagnética de la luz.
Esta teoría clásica tuvo (y continúa teniendo) grandes logros, pero también sufrió tropiezos fuertes. Al mismo tiempo que Hertz descubría las ondas electromagnéticas y Marconi las ponía al servicio de la humanidad, otros físicos la cuestionaban. Al unir la teoría de Maxwell a la termodinámica se produce la catástrofe ultravioleta; con la mecánica clásica, sus predicciones sobre el efecto fotoeléctrico, el espectro de los átomos y el efecto Compton son erróneas. Todo ello llevó a un puñado de físicos (la mayoría muy jóvenes) a construir en menos de 30 años una nueva física.
La mecánica cuántica, a diferencia de la clásica, es una teoría probabilística, donde las soluciones de las ecuaciones básicas sólo dan la probabilidad de que el sistema físico se halle en un estado u otro, pero nunca con certeza absoluta. La nueva física ha logrado explicar una enorme variedad de fenómenos con unos cuantos principios a la mano. Con ella hemos entendido las propiedades de los sólidos y se ha logrado dominar a los semiconductores, cuya influencia en la microelectrónica —y de ahí en nuestra sociedad industrial—, todo el mundo conoce. Con la teoría cuántica nos hemos adentrado en los misterios del núcleo atómico y lo hemos convertido en una fuente de energía que será, esperamos, limpia y segura a finales de este siglo. Con la física cuántica también hemos explorado el mundo subnuclear, el de las partículas elementales, tan pequeñas y veloces. Aunque mucho se ha avanzado en este terreno, el matrimonio de lo cuántico y lo relativista todavía no resulta tan armonioso como era de desearse. En fin, la física cuántica ha sido puesta a prueba en miles de experimentos, en infinidad de cálculos y ha dado origen a enormes desarrollos tecnológicos, como los transistores, los láseres, los reactores nucleares o los superconductores. Aunque seguramente no es la teoría física final, es sin duda el caballo de batalla de la ciencia hoy en día.
