XXX. LA SUPERCONDUCTIVIDAD Y LOS MONOPOLOS

ANTES de describir con detalle las ideas que sustentan el experimento que Blas Cabrera llevó a cabo, es conveniente hacer un paréntesis para presentar qué son los superconductores. Al hablar del campo magnético, hicimos un modelo para un alambre conductor, cuyo esquema presentamos en la Figura 8. En ese modelo del sólido conductor los electrones con carga negativa se movían al ser impulsados por un campo eléctrico externo, mientras que los iones permanecían quietos, a lo más oscilando respecto a su posición de equilibrio. La realidad es un poco más compleja, y sólo la mecánica cuántica nos puede explicar la diferencia entre un sólido que conduce electricidad y otro que es aislante. Es más, con la ayuda de la nueva física se han podido producir materiales cuya resistividad eléctrica se puede controlar. Estos materiales —los semiconductores— forman el corazón de los transistores, de los microcircuitos y de otros elementos básicos de la electrónica moderna, tecnología sin la cual es difícil imaginar a la sociedad actual.

En el párrafo anterior, el papel central lo juegan los electrones, sin que aparentemente intervengan, salvo en forma incidental, los iones. Del tipo de átomos que formen el sólido surge la estructura cristalina y la posibilidad de que los electrones se puedan mover más o menos libremente, lo que determina si el material es buen conductor o no. Sin embargo, hay un mecanismo en que intervienen tanto iones como electrones, mediante el cual un sólido se puede convertir en un superconductor.

Puesto que los iones se mueven oscilando, pensemos en un modelo para las vibraciones de la red cristalina que forman. El modelo es el siguiente: cada átomo se acopla a sus vecinos más cercanos por medio de algún tipo de resorte. Entre los posibles movimientos de los átomos así amarrados por resortes, existen unos, llamados modos normales, en que todas las partículas oscilan con la misma frecuencia. Al igual que en las oscilaciones electromagnéticas existen los cuantos de luz —los fotones que Einstein introdujo a la física—, a estos modos normales corresponden otros cuantos, que se llaman fonones. Estos fonones se parecen mucho a partículas microscópicas reales: tienen una velocidad y energía bien definidas. Por otro lado, no pueden existir sin la malla de átomos, es decir, fuera del cristal. Además, aumentando la energía de vibración del sólido, los átomos oscilan más, es decir, se crean más fonones. Si, por otro lado, enfriamos el cristal logramos que haya menos fonones. En consecuencia, los fonones se pueden crear y destruir.

Los fonones son los responsables directos de muchos fenómenos en los sólidos. En particular, causan la resistencia eléctrica, pues interfieren con los electrones. Al bajar la temperatura, los átomos se aquietan y desaparecen los fonones. Ya muy cerca del cero absoluto, puede darse que un electrón jale a los iones vecinos a él, por mera atracción eléctrica, y que estos iones a su vez atraigan a otro electrón que deambule por ahí. Este efecto, que ilustramos en la Figura 24, puede lograr que los dos electrones se unan para viajar juntos por el cristal, moviéndose sin dificultad. Hemos así encontrado un material de bajísima resistencia, de muy alta conductividad: ñestaremos frente a un superconductor!

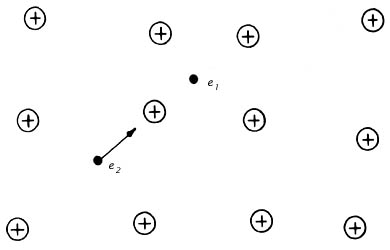
Figura 24. Un electrón e₁ atrae a los iones positivos vecinos, y éstos a su vez al otro electrón e₂ que deambula por ahí.

Esta explicación de la superconductividad se dio apenas hace veinticinco años. El fenómeno superconductor a bajas temperaturas, sin embargo, es conocido desde principios de siglo, cuando el físico holandés Kammerlingh Onnes pudo licuar helio y obtener temperaturas tan bajas como 0.8 kelvin sobre el cero absoluto. Con estas bajas temperaturas, Onnes descubrió la superconductividad.

El estado superconductor es muy diferente al estado normal de los sólidos. Como ya dijimos, un superconductor presenta una resistencia eléctrica muy baja; además, no permite que un campo magnético penetre en su interior; en fin, representa toda una fase diferente, que es una manifestación macroscópica de efectos cuánticos. Uno de estos efectos, conocido como la cuantización del flujo, es el siguiente: si una supercorriente fluye en un anillo superconductor, el campo magnético que produce a su alrededor debe ser tal que su flujo a través del anillo (es decir, el número de líneas de campo magnético que cruzan una superficie bordeada por el anillo, como se ve en la Figura 25) debe ser un múltiplo entero de la cantidad c/2e.

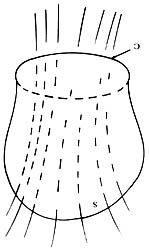
Figura 25. El flujo magnético es el número de líneas de campo que cruzan cualquier superficie —como la S de la figura que bordea el anillo C.

Si comparamos este valor del flujo magnético cuantizado con el valor predicho por Dirac para la carga magnética, m = c/4p e, nos damos cuenta de inmediato que los anillos superconductores constituyen antenas naturales para detectar el monopolo. Cuando una carga magnética cruzara por el anillo el flujo magnético se alteraría, con lo cual tendríamos una traza inequívoca de la presencia del monopolo. Cabrera calcula la corriente inducida como función de la distancia al centro del anillo superconductor, cuando un monopolo se acerca a lo largo del eje del alambre. El resultado se ve en la Figura 26, donde vemos que al paso del monopolo la corriente sufre un brinco y luego permanece constante.

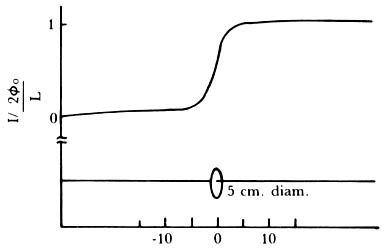
Figura 26. La corriente en el anillo superconductor cuando un monopolo lo cruza.

Con lo hasta aquí dicho, hemos completado finalmente la exposición de los conceptos físicos que se hallan detrás de un experimento como el de Cabrera. Y podemos, por fin, apreciar lo que significa hacer física y gozar la descripción de lo que es un experimento bien hecho.