IX. MUY BAJAS TEMPERATURAS

LA DESCRIPCIÓN microscópica presentada en el capítulo anterior supone que la dinámica que rige el movimiento de las partículas del fluido y el de la partícula browniana es la dinámica clásica, es decir, que los movimientos se rigen por medio de las ecuaciones de Newton. Sin embargo, en ciertas circunstancias, por ejemplo a bajas temperaturas, estas ecuaciones ya no rigen su descripción dinámica. Entonces la descripción que se tiene que hacer es cuántica.

Diremos unas cuantas palabras acerca de la mecánica cuántica. A principios del presente siglo varios investigadores como Max Planck, Albert Einstein, Niels Bohr, etc., se dieron cuenta de que varios fenómenos no podían explicarse usando la mecánica desarrollada por Newton, por ejemplo, la estructura de los átomos (véase el capítulo XI más adelante) o el comportamiento de las sustancias a muy bajas temperaturas. En general, se encontró que la descripción de los fenómenos microscópicos no puede hacerse tomando como base la mecánica newtoniana. Durante la década de 1920 se desarrolló una nueva mecánica, la cuántica, con la que sí se pudo dar una explicación satisfactoria de comportamientos microscópicos. Se descubrió que es precisamente con la mecánica cuántica con la que se tienen que describir todos los fenómenos. Pero resulta que si nos restringimos a cuerpos de masas muchísimo mayores que las masas atómicas, por ejemplo cuerpos macroscópicos que nos rodean cotidianamente, como pelotas, coches, edificios, etc., entonces la explicación cuántica coincide con la newtoniana.¹

Hay que mencionar que no siempre tiene sentido físico trasponer la descripción de un sistema clásico a uno cuántico. Así, por ejemplo, no tiene caso intentar describir cuánticamente una partícula inmersa en un líquido a muy bajas temperaturas, porque para aquellas temperaturas en casi todos los casos en que efectos cuánticos pueden aparecer, el líquido ya se habrá solidificado. Sin embargo, hay sistemas físicos de interés para los cuales sí tiene sentido físico (y es necesario) llevar a cabo una descripción cuántica. Solamente mencionaremos algunos sistemas: el movimiento de una partícula masiva en un sólido compuesto de partículas ligeras, el caso de una partícula eléctrica inmersa en un campo de radiación electromagnética fluctuante, un láser, entre otros. Haremos una breve presentación de los resultados que se han obtenido para estos casos.

El modelo de osciladores armónicos expuestos en el capítulo VIII se ha utilizado para tratar, dentro de ciertos límites, un sólido. Asimismo se puede demostrar que un campo electromagnético es equivalente a un conjunto de osciladores armónicos sin masa. En consecuencia, una partícula (con masa) eléctricamente cargada en interacción con el campo electromagnético es equivalente a una partícula en interacción con un conjunto de osciladores armónicos. Por lo tanto, el modelo de osciladores armónicos se puede aplicar a estos sistemas físicos.

Consideremos las mismas condiciones señaladas en el capítulo VIII, a saber:

1) El número N de átomos que forman el medio es muy grande. Así, se garantiza que los procesos son irreversibles. También en este caso, el cuántico, existe un teorema de recurrencia de Poincaré análogo al del caso clásico.

2) La masa de la partícula browniana es muchísimo mayor que la masa de cada uno de los átomos del medio.

3) Se tratará con tiempos muy grandes comparados con el tiempo que tardan en ocurrir dos colisiones entre las partículas.

Bajo estas circunstancias se encuentra que, efectivamente, la partícula browniana experimenta de nuevo dos fuerzas, análogas a las del caso de altas temperaturas. Con respecto a la primera de estas fuerzas la situación es idéntica a la analizada anteriormente.

Sin embargo, la fuerza estocástica ya no tiene las mismas propiedades que a altas temperaturas. Mientras que clásicamente la fuerza no está correlacionada consigo misma en cualquier otro instante, en el caso cuántico existe una correlación y puede durar un tiempo t_q muy grande (E. Braun, 1967). En la figura 22 se muestra la gráfica de la dependencia de este tiempo de correlación t_q con la temperatura. A medida que la temperatura del medio se hace más baja, el tiempo de correlación se vuelve cada vez más grande. Es decir, se presenta un fenómeno de persistencia de las fluctuaciones (K. Lindenberg y B. West, 1984; E. Braun, 1985). Una característica muy interesante de este tiempo t_q es que es universal. Con esto queremos decir que no depende de ninguna característica del sistema, salvo de su temperatura. Esto constrasta con el tiempo de relajación t obtenido para el caso de altas temperaturas, que sí depende de las características particulares del sistema. En otras palabras, dos sistemas distintos a la misma temperatura, tienen distintos valores de t, mientras que tienen el mismo valor de t_q .

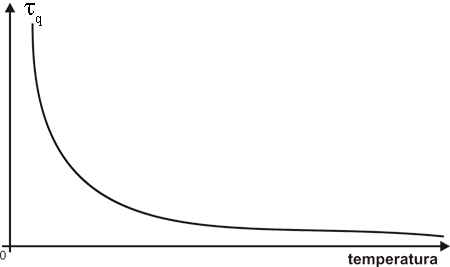
Figura 22. El tiempo de correlación cuántico t_q como función de la temperatura. A medida que la temperatura disminuye el tiempo aumenta.

Una consecuencia de lo anterior es que el valor cuadrático medio de las velocidades ya no decae con un solo tiempo de relajación como ocurre en el caso clásico, sino que aparece, además, el nuevo tiempo de relajación cuántico t_q. Debe mencionarse que aun en estas condiciones resulta que el promedio de la velocidad decrece como en el caso de altas temperaturas; es decir, con el tiempo de relajación t introducido arriba.

Si la temperatura t es suficientemente baja, vemos de la gráfica que t_q grande y por lo tanto existe un régimen de tiempos t tales que son muchos mayores que el tiempo de relajación t por un lado, y por el otro, mucho menores que el tiempo de relajación cuántico t_q (ver la figura 23).

En este régimen de tiempos, el valor cuadrático medio de la velocidad de la partícula no ha alcanzado todavía su valor de equilibrio, en contraste con el caso clásico en que para estos tiempos la partícula ya habría llegado a equilibrio y, por tanto, habría "olvidado" sus condiciones iniciales.

Figura 23. A temperaturas suficientemente bajas el tiempo t puede ser mucho mayor que el tiempo de relajación t, pero mucho menor que el tiempo cuántico t_q.

En el caso clásico, como se vio anteriormente, el promedio de la velocidad de la partícula browniana decae en un tiempo t; esta disipación se debe a la fricción (o viscosidad) que se genera entre el medio y la partícula, cuando ésta se mueve en el medio. Por otro lado, como vimos, el valor cuadrático medio de la velocidad también decrece con el mismo tiempo de relajación t.

En el caso cuántico, a temperaturas suficientemente bajas, las cosas son distintas. Se presentan dos escalas de relajación diferentes: la debida a la fricción viscosa dada por t y la de origen cuántico dada por t_q. Lo anterior tiene como consecuencia que, en el caso clásico, el mecanismo de disipación viscosa relaja una fluctuación que haya ocurrido en el sistema por cualquier motivo. La fluctuación desaparece y el sistema regresa al equilibrio. En el caso cuántico esta descripción ya no es cierta. Las fluctuaciones a bajas temperaturas dejan de relajarse y por lo tanto la disipación viscosa no lleva al sistema al equilibrio.

Otra interesante consecuencia es la siguiente: dado que las cantidades físicas que acabamos de señalar determinan las propiedades macroscópicas, termodinámicas, del sistema, este efecto de la persistencia de las fluctuaciones debe ser observable. Hay que mencionar que diversas facetas de este problema todavía son hoy materia de investigación.

Es interesante anotar que el comportamiento cuántico que acabamos de presentar se ha obtenido a partir de una base microscópica. A diferencia del caso clásico, no existía antes una teoría fenomenológica (o empírica) cuántica en busca de fundamentación. Antes del desarrollo de las teorías cuánticas microscópicas no se había encontrado la forma de atacar el problema. Éste es un buen ejemplo de la superioridad de las teorías microscópicas, que estudian con mayor profundidad los comportamientos de los sistemas macroscópicos.

NOTAS

1 Para una explicación más amplia véase E. Braun, Una faceta desconcida de Einstein, México, FCE, 1986.