VIII. DESCRIPCIÓN MICROSCÓPICA

EN LA sección anterior se reseñó la descripción macroscópica basada en las suposiciones hechas por Langevin. Como se recordará, Langevin supuso varias propiedades de las fuerzas, tanto sistemáticas como estocásticas, que experimentan las partículas brownianas. Una vez aceptadas estas suposiciones se pudieron encontrar conclusiones acerca de las propiedades que deben tener las distribuciones tanto de la velocidad como de la posición. Estas conclusiones se compararon con resultados extraídos de experimentos, obteniéndose un buen acuerdo, lo que significa que las suposiciones hechas son adecuadas.

Sin embargo, uno podría pensar que la manera en que se hicieron las suposiciones es, en cierta forma, artificial. Cabe preguntar: ¿se podrían justificar más fundamentalmente estas suposiciones? En particular, y como el lector podrá haber advertido, al proponer dichas suposiciones no se tomó en cuenta, en detalle, el hecho de que las sustancias en cuestión, por ejemplo el fluido, están constituidas por átomos, es decir, que tienen una estructura microscópica.

Dedicaremos pues esta sección a estudiar más a fondo la descripción microscópica del movimiento browniano. En este tipo de tratamiento se adaptan las ideas desarrolladas en la teoría cinética de la materia, ya descritas en el capítulo II. La aplicación de estas ideas al movimiento browniano se inició hacia fines de la década de los años 50 y continúa, de hecho, hasta hoy.

La idea general del enfoque microscópico es suponer la forma de las fuerzas que los átomos se aplican entre sí y con la partícula browniana. Con esto se plantean las ecuaciones mecánicas que describen el movimiento de cada partícula del sistema fluido-partícula browniana, por ejemplo, las que se obtienen de aplicar la segunda ley de Newton. Si N es el número de átomos en el fluido, entonces se obtendrán (N + 1) ecuaciones de este tipo. Estas ecuaciones resultan muy complicadas, ya que, en general, una partícula puede interaccionar con cada una de las demás que componen el sistema (Figura 19). En general, no se han podido resolver exactamente estas ecuaciones. El procedimiento que se debe seguir es tratar de encontrar la solución para la partícula browniana, y ver qué influencia tienen sobre ella las demás partículas del sistema.

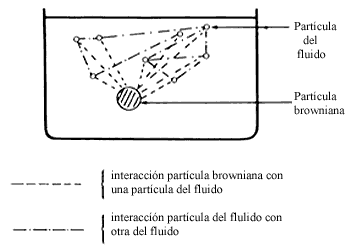
Figura 19. En el sistema partícula browniana-fluido cada una de las partículas componentes interacciona con todas las demás. En la figura solamente se indican algunas de estas interacciones.

Uno de los métodos seguidos es suponer que la masa de la partícula browniana es muchísimo mayor que la masa de cualquiera de los átomos que componen el fluido. Para los casos usuales la masa de la partícula browniana es unas 300 millones de veces más grande que la masa de un átomo del fluido. En estas condiciones, ocurre que las velocidades de cada una de las partículas del fluido son muchísimo mayores que las velocidades que tiene la partícula browniana. Con ayuda de este hecho se ha podido encontrar, para un fluido, la solución de manera aproximada. Hay que mencionar, sin embargo, que el desarrollo de este programa para fluidos está plagado de dificultades matemáticas, que todavía no han podido ser resueltas.

En vista de lo anterior, se ha intentado estudiar otro tipo de modelos para los cuales se puedan obtener resultados exactos, simplificando matemáticamente el modelo pero manteniendo suficiente contenido físico para que siga siendo de interés. Estos trabajos fueron realizados principalmente por P. C. Hemmer (1959), R. Rubin (1960), G. Ford, M. Kac y P. Mazur (1965), P. Mazur y E. Braun (1964). Los modelos llamados genéricamente de osciladores armónicos acoplados satisfacen los requisitos mencionados.

Se han estudiado estos modelos en una, dos y tres dimensiones. Sin embargo, las ideas físicas fundamentales que se manejan y los resultados que se obtienen en los modelos de una dimensión son, en esencia, los mismos que se presentan al tratar con otras dimensionalidades. Así que, para simplificar, analizaremos a continuación modelos de osciladores armónicos en una dimensión. Esto significa que cada uno de los átomos o moléculas de nuestro sistema solamente se puede mover a lo largo de una línea recta.

Imaginemos un conjunto de partículas colocadas a lo largo de una línea recta, en posiciones equidistantes. Supongamos ahora que entre cada pareja de partículas adyacentes hay un resorte (Figura 20). Si, por algún motivo, cualquiera de las partículas se mueve, nos podemos dar cuenta que después de cierto tiempo todas las demás partículas habrán de moverse. Esto se debe a que todas las partículas están acopladas entre sí por medio de resortes, aunque la interacción directa de una partícula sea solamente con sus dos vecinas próximas. A este sistema se le llama conjunto de osciladores armónicos. En este modelo, una de las partículas, la de masa grande, desempeñará el papel de la browniana, mientras que todas las demás, de masas pequeñas, representarán al fluido.

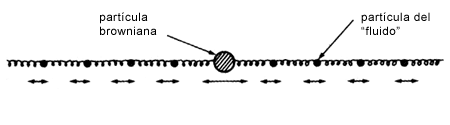
Figura 20. Modelo en una dimensión de un conjunto de osciladores armónicos. La partícula grande desempeña el papel de la browniana y el resto de ella el del fluido.

Se ha podido resolver en forma exacta el sistema de ecuaciones de movimiento de todo el conjunto de partículas. La solución que corresponde a la partícula browniana se puede expresar de la siguiente forma:

En primer lugar para este modelo se ha podido estudiar con bastante detalle, la manera en que la evolución de la partícula browniana resulta irreversible. Para poner en el contexto adecuado esta cuestión, debemos mencionar que las ecuaciones de Newton, resultantes de su segunda ley, son ecuaciones que describen procesos reversibles. Entonces surge la pregunta: ¿cómo es posible que si la dinámica esencial del movimiento de las partículas del sistema es reversible, pueda ocurrir que la evolución de la partícula browniana sea irreversible? Este problema fue planteado en 1876 por Josef Loschmidt (1821-1895) y se le conoce como la paradoja de la reversibilidad.

Loschmidt planteó esta paradoja en forma general. De hecho dudaba que fuera posible, en principio, hacer la descripción que se intenta. Esto ocurría en tiempo en que todavía no se confirmaba la composición atómica de la materia.

Posteriormente, en 1896, Ernst Zermelo (187l-l953) planteó otra paradoja con la que trató de mostrar que no era posible suponer que la materia estuviese compuesta de átomos. Esta paradoja se basa en un famoso teorema general de la mecánica, el llamado teorema de recurrencia debido a Henri Poincaré (1854-1912), que dice: en un sistema mecánico con un número finito de partículas, los valores que adquieren en cierto instante las variables que lo describen volverán a repetirse tan cercanamente a los originales como se quiera, si uno espera un tiempo suficientemente grande.

El teorema de Poincaré nos dice que si en cierto instante tomamos una fotografía de las posiciones y de las velocidades de las partículas que componen un sistema arbitrario (Figura 21 (a)), y si esperamos un tiempo suficientemente grande, el sistema regresará a un estado que tendrá valores de las posiciones y de las velocidades de sus partículas muy cercanos a los originales (Figura 21 (b)). Es decir, el sistema recurre a su estado inicial, y la nueva fotografía deberá coincidir con la original, lo que significa que la evolución del sistema no es irreversible, sino reversible. Este teorema de recurrencia es una consecuencia del carácter reversible de los movimientos descritos por la mecánica. Este teorema, como fue aplicado por Zermelo, nos hace ver que, según la mecánica, los procesos irreversibles no pueden existir.

Por otro lado, como se analizó en el capítulo IV, sabemos de nuestra experiencia diaria que sí existen procesos irreversibles en la naturaleza.

Es claro que estas dos paradojas son un grave escollo para la descripción general de procesos irreversibles, en particular, para el sistema que estamos tratando.

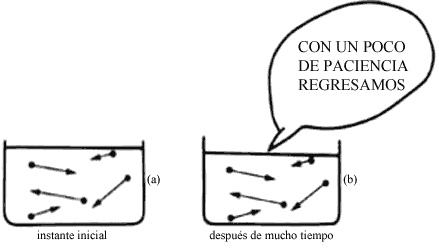
Figura 21. Si inicialmente un sistema tiene una configuración y ciertas velocidades (a), después de un tiempo suficientemente grande volverá a tener casi los mismos valores de sus posiciones y velocidades (b).

Afortunadamente la conciliación de estas paradojas se puede encontrar para el modelo de osciladores armónicos que estamos tratando. En efecto, es posible calcular el tiempo de recurrencia, es decir cuánto tiempo tarda un sistema, en un estado dado, en regresar a su estado inicial. Se ha hecho este cálculo para el caso de diez osciladores y se ha exigido que el sistema regrese a un estado en el que las posiciones recurran con un error menor o igual a 3%. Esto es, se quiere que las posiciones de las partículas estén en el intervalo X_j +DX_j DX_j donde X_j son las posiciones iniciales de las partículas y los intervalos DX_j sean tales que Dx_j/x_j = 0.3. En 1959 Hemmer encontró que para que esto ocurra tiene uno que esperar, en promedio ñ10¹⁰ años! (un uno seguido de diez ceros). ñEste tiempo es más grande que la edad del Universo! Y esto solamente para diez partículas....

A medida que el número de partículas N del sistema aumenta, el tiempo de recurrencia también aumenta. Como vemos, dichos tiempos son astronómicos. Esto quiere decir que un observador como el hombre, con tiempos de observación del orden de, digamos, siglos (o milenios), no tendrá oportunidad de darse cuenta de la recurrencia y sufrirá la sensación de que el fenómeno que estudia es irreversible.

Ahora bien, si el número de partículas N del sistema se hace extremadamente grande, por ejemplo, para tratar sistemas macroscópicos que contienen 10²⁰ partículas en cada centímetro cúbico de volumen, entonces el tiempo de recurrencia se vuelve prácticamente infinito. Lo que ocurre es que al aumentar N, el tiempo de recurrencia se hace tan grande que deja de haber recurrencia y el fenómeno físico se vuelve efectivamente irreversible.

Como conclusión podemos decir que el movimiento de la partícula browniana será irreversible si el número de las otras partículas con las que está acoplada, las del "fluido", es muy grande, y de esta manera se concilian satisfactoriamente las paradojas de Loschmidt y de Zermelo.

Del tratamiento exacto también se encuentra que efectivamente la partícula browniana experimenta dos fuerzas, como lo supuso Langevin. Sin embargo, es solamente bajo ciertas condiciones que estas dos fuerzas que aparecen ahora tienen las mismas características que les asignó este científico. Veamos ahora cada una de ellas por separado.

En primer lugar, se obtiene una fuerza que es proporcional a la velocidad de la partícula browniana. Sin embargo, para que esta fuerza sea efectivamente la fuerza viscosa de la que hablamos en el capítulo VI se deben cumplir dos condiciones:

1) La masa de la partícula browniana tiene que ser muchísimo más grande que la masa de cualquier átomo del fluido.

2) El régimen de tiempos tiene que ser muy grande comparado con el tiempo característico de la colisión entre dos partículas.

Físicamente esto quiere decir que para que la partícula pesada realice movimiento browniano debe haber transcurrido suficiente tiempo como para que haya recibido un número grande de impactos de las partículas que componen el fluido.

Bajo estas condiciones, la primera fuerza es justamente la viscosa y resulta que depende solamente de propiedades generales de las interacciones entre los átomos que componen el "fluido" y no de otros detalles específicos. Esto también está de acuerdo con las observaciones empíricas, ya que no importa qué tipo de partícula sea la pesada y en qué fluido se le introduzca: siempre que sea mucho más masiva que los átomos del fluido, realizará movimiento browniano.

Ahora consideremos las características de la otra fuerza que se obtiene del tratamiento teórico. Resulta que esta segunda fuerza depende de los valores iniciales de las posiciones y de las velocidades de los átomos que componen el fluido. En general, no hay manera de conocer estas cantidades con precisión. Lo que sí se sabe en las condiciones experimentales usuales es que el fluido en el que se introduce la partícula browniana está inicialmente en equilibrio a determinada temperatura. Esto quiere decir que en un principio las velocidades de los átomos del fluido están distribuidas de manera maxwelliana. Ello implica que las posiciones y velocidades iniciales son realmente cantidades estocásticas, que están distribuidas gaussianamente. Por lo tanto, la segunda fuerza es una combinación de cantidades estocásticas gaussianas (las velocidades y posiciones de las partículas del fluido), y en consecuencia, como se puede demostrar en estadística matemática, es una cantidad estocástica gaussiana.

Si además se cumplen las condiciones de los incisos 1) y 2), se puede demostrar que el promedio y la desviación estándar de esta fuerza estocástica tienen justamente las propiedades supuestas por Langevin, descritas en el capítulo VI. En particular, resulta que las fuerzas estocásticas no están correlacionadas en distintos instantes de tiempo. Es decir, las fluctuaciones decaen muy rápidamente.

De esta manera vemos cómo a partir de un modelo microscópico se pueden justificar las suposiciones fenomenológicas de Langevin para descubrir el movimiento browniano.

Para finalizar este capítulo recordaremos al lector que este programa sólo se ha podido llevar a cabo, con toda plenitud, para el modelo de osciladores armónicos. Para otros tipos de sistemas, el problema continúa abierto.