XI. OTROS TIPOS DE SISTEMAS QUE SE COMPORTAN ANÁLOGAMENTE: LOS LÁSERES

HASTA este momento se ha estudiado el movimiento browniano que realiza una partícula grande al trasladarse dentro de un fluido. Este movimiento azaroso y estocástico también se presenta en otros sistemas físicos. Haremos una revisión breve de algunos de ellos.

En el tratamiento presentado en los capítulos anteriores se ha supuesto, aunque no se mencionó, que las partículas brownianas bajo consideración eran, de hecho, partículas puntuales. No se trató para nada la posibilidad de que tuviesen cierta estructura. Por eso sólo se consideró el movimiento de traslación de su centro de masa. Sin embargo, las partículas de que hablamos son, en general, agregados de moléculas que sí tienen estructura. Esto significa que además de trasladarse, también pueden realizar un movimiento de rotación alrededor de su centro de masa (Figura 30).

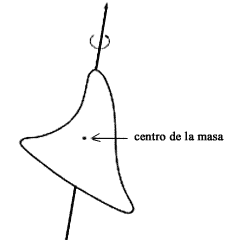
Figura 30. Una partícula con estructura, además de trasladarse, puede girar alrededor de su centro de masa.

Al chocar dos partículas que tienen estructuras, además de intercambiar velocidades, lo que da lugar a una modificación del movimiento de sus centros de masa, pueden también modificar sus movimientos de rotación. Dado que la partícula tiene estructura, girará alrededor de cierto eje; resulta entonces que si una partícula grande se introduce en un fluido, debido a las colisiones con las moléculas que forman el fluido la dirección del eje de rotación cambiará. Por el mismo tipo de argumentos presentados antes, y ya que el número de colisiones por segundo que experimenta la partícula es extraordinariamente grande, el resultado neto es que la dirección de su eje de rotación cambiará continuamente y de manera azarosa (Figura 31). Einstein desarrolló la teoría de este fenómeno al que denominó movimiento browniano rotacional.

Figura 31. Ilustración de movimiento browniano rotacional.

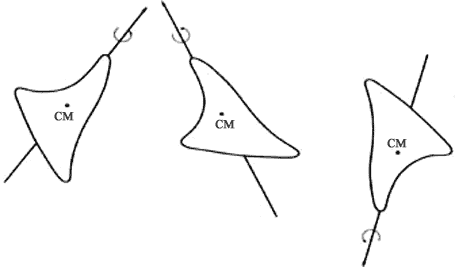
El hecho de que el eje de rotación cambie azarosamente significa que los ángulos que determinan la dirección de este eje cambian en forma estocástica al transcurrir el tiempo. En consecuencia, al igual que antes, en este caso también se puede hablar de una distribución de los valores que adquieren los ángulos. De manera análoga a la que usó en el caso traslacional, Einstein obtuvo que el valor cuadrático medio de la distribución de los ángulos debería tener una variación lineal con el tiempo, para tiempos más grandes que un valor determinado. La constante de proporcionalidad depende de la temperatura, la viscosidad, la forma de la partícula y sus dimensiones.

Fue el mismo Jean Perrin quien en 1909 verificó, primero, la existencia de este tipo de movimiento, y luego la predicción de Einstein acerca del valor cuadrático medio de la distribución de los ángulos. Perrin usó para ello partículas de mastique de alrededor de 0.013 mm de diámetro. Al igual que en el caso traslacional, de estos resultados también se puede inferir el valor del número de Avogadro. Perrin lo hizo y obtuvo una buena concordancia con el valor que encontró para el caso traslacional, así como con los valores obtenidos para otros fenómenos independientes.

Se han encontrado las distribuciones de las velocidades angulares, en el caso de movimiento browniano rotacional: para ello se hacen consideraciones análogas a las de Langevin para el caso traslacional. Si la molécula browniana tiene una estructura esférica entonces la distribución es gaussiana (P. Hubbard, 1977). Si la molécula tiene una estructura de un cuerpo de revolución, como por ejemplo un trompo, resulta que la distribución no es gaussiana, sino que tiene una forma mucho más complicada (P. Hubbard, 1979; E. Braun y E. Cortés, 1986). Para moléculas con estructura arbitraria todavía no se ha encontrado la distribución en forma exacta.

La existencia del fenómeno de rotación browniana tiene algunas consecuencias importantes. Por ejemplo, podemos considerar el caso de una suspensión de partículas con estructura, que tenga carga eléctrica o dipolo magnético. Si no hubiera rotación browniana, al aplicar a la suspensión un campo eléctrico o magnético externo todas las partículas se alinearían al campo (Figura 32). Esto significa que cada una de estas partículas debería girar alrededor de un eje, el AA', que es paralelo a la dirección del campo. Sin embargo, si el fenómeno de rotación browniana existe, estos ejes cambian de dirección, aun en presencia del campo externo (Figura 33). Según el resultado de Einstein, el ancho de la distribución de la orientación de los ejes de rotación depende, entre otras cosas, del tamaño y forma de las partículas coloidales, idea que provee un método para medir estas cantidades. Es así como, por el fenómeno de rotación se han determinado las dimensiones de algunas sustancias como, por ejemplo, los virus.

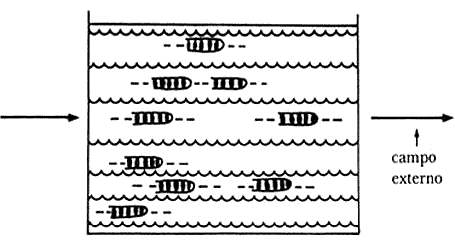
Figura 32. Al aplicar una fuerza externa las moléculas se deberían alinear.

Otros sistemas en el que se han utilizado las ideas desarrolladas para el caso del movimiento browniano es el láser. El láser es un dispositivo que puede producir haces de luz con características muy especiales: los haces están muy colimados y tiene una intensidad mucho más alta que la que se obtiene con fuentes convencionales de luz.

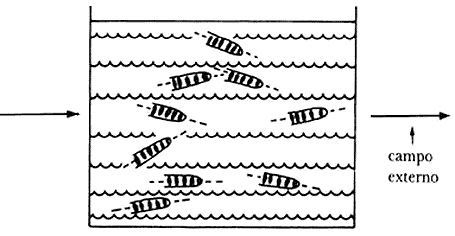
Figura 33. El movimiento browniano rotacional impide el alineamiento completo de las moléculas.

Daremos una breve explicación del funcionamiento de un láser: los átomos y moléculas son entes que tienen valores (o niveles) de energía bien definidos. El estado con el valor más bajo de la energía se llama estado base, mientras que los otros, con valores mayores de la energía, se llaman estados excitados (Figura 34). A la secuencia de niveles mostrada en la figura 34 se le llama el espectro de energía del átomo o molécula en cuestión. Distintos átomos o moléculas tienen distintos espectros de energía. En cualquier instante el átomo sólo puede tener una de las energías de sus niveles; es decir, el átomo no puede tener una energía con un valor que se encuentre entre los valores de dos de sus niveles. Se dice que la energía está cuantizada. Al ocurrir determinados procesos con el átomo, éste puede cambiar su energía, por ejemplo, a causa de una colisión, de una descarga eléctrica o de calentamiento. En tal caso, el átomo pasará del nivel de energía en que se encuentra a otro diferente. Por ejemplo, puede pasar del estado base al primer estado excitado, o al segundo estado excitado, etc., pero solamente puede empezar y terminar en alguno de los niveles de su espectro. Esto significa que en las transiciones en que se ve involucrado el átomo, los cambios de energía que puede experimentar son iguales a las separaciones DE₁. DE₂... que corresponden a las diferencias de las energías entre cualquier pareja de sus niveles (Figura 34). Así, se dice que hay una transición entre los niveles involucrados. Por otro tipo de motivos que no vienen en este momento al caso, puede ocurrir que alguna de estas transiciones esté prohibida.

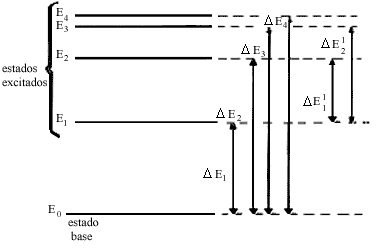
Figura 34. Niveles de energía de un átomo.

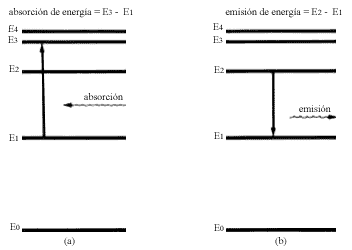
Figura 35. Al pasar el átomo de un nivel bajo a uno más alto lo hace absorbiendo energía
(a). Si pasa de un nivel alto a uno más bajo emite energía (b).

Si la transición es de un nivel bajo a otro superior (Figura 35, (a)), se dice que el átomo absorbe energía (igual a la diferencia entre los valores de las energías de dichos niveles), mientras que si pasa de un nivel alto a otro más bajo (Figura 35, (b)), se dice que el átomo emite energía (igual a la diferencia entre los valores de las energías de dichos niveles). Lo anterior significa que un átomo sólo puede absorber o emitir energía en cantidades perfectamente determinadas que, como se acaba de señalar, son iguales a los valores de las diferencias de las energías entre las parejas de niveles cuyas transiciones sean permitidas.

Ahora bien, si un átomo está en un nivel excitado, al ocurrir una transición a un nivel más bajo emite energía en forma de radiación electromagnética. La frecuencia de esta onda emitida es proporcional a la energía emitida, es decir, a la separación entre los niveles en cuestión. Si resulta que la frecuencia tiene el valor entre los límites del espectro visible, el átomo estará emitiendo ondas electromagnéticas que el ojo humano pueda registrar como luz visible. Dado que la frecuencia de la radiación está asociada al color que le asignamos (si está dentro de la región visible) lo anterior significa que determinado átomo sólo puede emitir ciertos colores perfectamente característicos.

Asimismo, el átomo puede absorber energía electromagnética pasando de un nivel a otro de mayor energía. Pero, de lo que acaba de señalar arriba, vemos que solamente puede absorber una energía con valores muy precisos, es decir, sólo podrá absorber la radiación electromagnética con una frecuencia determinada. Si sobre el átomo incide radiación electromagnética cuya frecuencia tenga un valor distinto a cualquiera de los mencionados, entonces el átomo no absorbe dicha radiación; en este caso el átomo es transparente a la radiación incidente.

Si se tiene un conjunto de átomos, por ejemplo los que componen un gas que está en equilibrio a una temperatura dada, la mayoría de ellos se encuentran en su estado base; otro número menor de átomos se encuentra en el primer estado excitado, y a su vez otro número más pequeño todavía se encuentra en el segundo estado excitado y así sucesivamente. Si en estas condiciones se iluminan los átomos con luz de una frecuencia que corresponda a la diferencia de energía entre el estado base y el primer excitado, digamos, el gas absorberá energía de la radiación, ya que hay un número de átomos más grande en el estado base que en el primer estado excitado. En estas circunstancias disminuye la intensidad del campo de radiación, porque parte de su energía ha sido absorbida.

Supongamos que de alguna manera se lograra que en un gas hubiera más átomos en el primer estado excitado que en el estado base. Esta situación no es de equilibrio. En estas condiciones los átomos pasarán en mayor número del estado excitado al base, es decir, habrá emisión neta de energía del átomo al campo de radiación. Si la cantidad de energía proporcionada por los átomos es mayor que las inevitables pérdidas que ocurren, la intensidad de la radiación aumentará. El proceso por el que se logra la inversión de la población de los niveles de energía se llama bombeo óptico, y constituye la fuente de energía de la radiación resultante.

Ahora bien, cuando un átomo se encuentra en un estado excitado, puede ocurrir la transición a un estado de energía más bajo, con la consecuente emisión de radiación, en forma espontánea. Einstein demostró, en 1917, que si un átomo excitado se encuentra dentro de un campo de radiación electromagnética, también puede ocurrir otro proceso de emisión, inducido por el campo. Mientras mayor sea la intensidad del campo, mayor será la probabilidad de que ocurra la emisión inducida. Si no hay campo presente, es claro que no hay esta emisión.

Las radiaciones emitidas en forma espontánea e inducida que ocurren en los átomos de un gas tienen características distintas. La radiación espontánea que emite cada átomo ocurre en forma azarosa. Esto tiene como consecuencia que, por ejemplo, las fases de la radiación emitida por dos átomos sean, en general, completamente independientes una de la otra. Se dice que esta muestra de gas emite ondas que están desfasadas (Figura 36, (a)). Por otro lado, cuando hay emisión inducida, las ondas resultantes están en fase (Figura 36, (b)). Cuando dos ondas se unen, la amplitud neta que adquieren depende de la diferencia de fases que haya entre ellas. Si las ondas están desfasadas, la intensidad resultante es bastante baja, y puede incluso ser nula, mientras que si no hay diferencia de fase, la intensidad resultante es bastante grande. Por tanto, la intensidad de la radiación inducida es mucho mayor que la de la radiación espontánea.

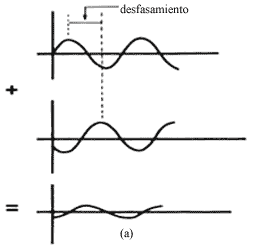
Figura 36. (a) Dos ondas desfasadas que interfieren. El resultado es una onda de muy pequeña amplitud.

Un láser es un dispositivo que emite radiación inducida. Las fuentes convencionales de luz que nos son familiares, por ejemplo un foco eléctrico, emiten radiación espontánea. En consecuencia, la intensidad de la luz emitida por un láser es muchísimo mayor que la emitida por las fuentes de luz convencionales.

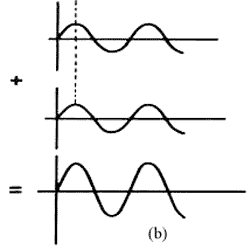
36.(b) Dos ondas en fase que interfieren. El resultado es una onda de amplitud grande.

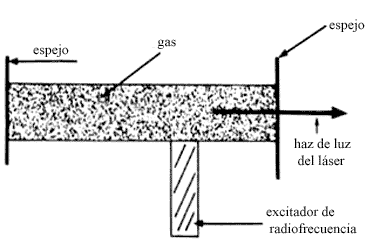
En la figura 37 se muestra un esquema de un láser. El tubo contiene el gas que va a producir la emisión inducida de luz. Se escoge este gas de manera que sus niveles de energía proporcionan radiación en la frecuencia de interés. Por ejemplo, se usan gases como la mezcla de helio-neón o de bióxido de carbono. En cada extremo del tubo hay un espejo. El bombeo, o sea la inversión de la población, se logra por medio de una descarga de radiofrecuencia, proporcionada por el excitador mostrado. Una vez que los átomos empiezan a emitir por inducción, la intensidad de la radiación aumenta. Los espejos reflejan la luz hacia el gas con el fin de que la intensidad de radiación presente sea grande y así aumente la probabilidad de la emisión inducida. De hecho, éste es un mecanismo de retroalimentación. Es así como la luz generada de esta manera alcanza intensidades muy altas.

La palabra láser es un acrónimo, en inglés, de amplificación de luz por emisión de radiación estimulada (o inducida).

En general, resulta que la intensidad del campo de radiación no tiene un valor constante, ni tampoco ocurre que varíe en forma gradual al transcurrir el tiempo. Este campo experimenta fluctuaciones en el valor de su intensidad, y éstas son al azar; es decir la intensidad del campo es una cantidad estocástica.

Por otro lado, debido a que la emisión inducida que ocurre depende del valor que tenga la intensidad del campo, entonces cuando los átomos de un láser se encuentren dentro del campo de radiación emitirán en forma estocástica. El resultado neto es que, tanto el campo como los átomos, se comportan estocásticamente.

Figura 37. Esquema de un láser.

Se puede pensar que el átomo se encuentra inmerso en un "fluido" (que es el campo de radiación) con el cual experimenta "colisiones" (la interacción entre el átomo y el campo) y que, dada la estocasticidad del "fluido" su comportamiento (el del átomo) es azaroso. Entonces, la descripción completa de un láser debe ser estocástica. Nos encontramos con que el átomo que se encuentra dentro de un campo de radiación electromagnética se comporta en forma análoga a una partícula browniana inmersa en un fluido. Se puede, en consecuencia, hablar de distribuciones de diversas cantidades relacionadas con la luz emitida. Se ha encontrado que se pueden describir las propiedades estadísticas del láser usando las ideas del movimiento browniano a bajas temperaturas. Esto se debe a que láser es un dispositivo cuántico.