XII. ALGUNAS COSAS RARAS COMO LOS FRACTALES
EN LAS últimas dos décadas se ha desarrollado una nueva línea de investigación, iniciada por Benoit Mandelbrot: los fractales.
Si regresamos al capítulo III, donde se explicó la forma en que se encuentra la trayectoria que sigue una partícula browniana, mostrada en la figura 1, resulta que, en rigor, las líneas rectas allá mostradas no tienen ninguna realidad física. Las posiciones sucesivas en cada intervalo de tiempo, cada 30 seg digamos, se marcaron con un punto y luego estos puntos se unieron sucesivamente con líneas rectas. Por tanto, lo único que tiene realidad son los puntos, las posiciones de la partícula browniana al final de cada intervalo. Si ahora en vez de marcar las posiciones en cada intervalo de 30 seg se marcaran en cada intervalo de 3 seg, y se unieran los puntos con líneas rectas, cada línea recta de la figura 1 quedaría reemplazada por una sucesión de líneas quebradas de menor tamaño, pero de igual complejidad (Figura 38). Así, por ejemplo, entre dos puntos sucesivos, como los A y B de la figura 1 (Figura 38, (a)), se obtendrán los puntos mostrados en la figura 38(b)). Concluimos ahora que la figura que se forma tiene el mismo tipo de estructura que la de la figura 1. Se podría ahora tomar intervalos de 0.3 seg y seguir el mismo procedimiento y ocurriría lo mismo que antes. Nos damos cuenta de que la trayectoria que sigue una partícula browniana es tal que continúa teniendo una estructura similar al cambiar la escala de tiempo de la observación. Este tipo de línea fue denominado fractal por Mandelbrot. Un objeto que presenta la misma estructura al cambiarle indefinidamente la escala de observación es un fractal.
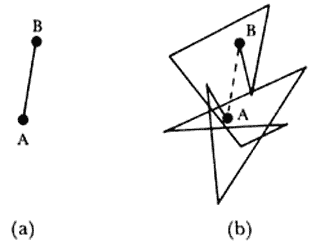
Figura 38. (a) Posiciones de la partícula browniana al inicio y al final de un intervalo de tiempo. (b) Posiciones de la misma partícula browniana al registrarlas en intervalos que son la décima parte del intervalo anterior.
Es interesante notar que ya en 1906 Jean Perrin se había dado cuenta de este tipo de comportamiento. En particular había llamado la atención sobre el hecho de que si uno toma un punto de la trayectoria que sigue una partícula browniana entonces, en rigor, no se puede trazar una línea tangente a ella. Él escribió entonces: "... Usando lenguaje geométrico, curvas que no tienen tangente son la regla, y curvas regulares, tales como el círculo, son interesante pero especiales.
"A primera vista la consideración del caso general puede aparecer un mero ejercicio intelectual, ingenioso pero artificial. Los que oyen de curvas sin tangente tienden a pensar que la naturaleza no presenta tales complicaciones, ni siquiera la sugiere.
"Sin embargo, lo contrario es la verdad. Esta afirmación se puede ilustrar considerando ciertos valores experimentales sin preconcepción.
"Considérese, por ejemplo, uno de los copos blancos que se obtienen al añadir sal a una solución jabonosa. A cierta distancia, su contorno puede dar la sensación de estar nítidamente definido, pero a medida que nos acercamos, esta nitidez desaparece. El ojo ya no puede dibujar una tangente en cualquier punto. Una línea que a primera vista parecería ser satisfactoria, bajo un escrutinio detallado resulta ser perpendicular u oblicua. El uso de una lupa o de un microscopio nos deja más inciertos, ya que aparecen nuevas irregularidades cada vez que aumentamos la magnificación, y nunca logramos conseguir una impresión nítida, lisa como la dada, por ejemplo, por una bola de acero..."
Y continúa Perrin: .... la característica esencial de nuestro copo es que cualquier escala involucra detalles que prohiben absolutamente la fijación de una tangente.
"Estaremos dentro del dominio de la realidad experimental cuando observamos bajo el microscopio el movimiento browniano con que se agita una partícula (browniana) suspendida en un fluido. Se encuentra que la dirección de la línea recta que une las posiciones ocupadas en dos instantes muy cercanos en el tiempo varía irregularmente en forma absoluta a medida que el intervalo entre los dos instantes se hace menor. Un observador sin prejuicios concluiría, en consecuencia, que está tratando con una curva a la que no se le puede dibujar una tangente."
Tomemos ahora otro caso, por ejemplo el de una costa. Consideremos dos puntos cualesquiera, digamos A y B (Figura 39). Si primero la observamos en un mapa de escala 1/100 000 nos daremos cuenta de que tiene algunas bahías y penínsulas, por ejemplo. Si en seguida volvemos a examinar la misma costa, pero ahora en un mapa que tenga la escala de 1/10 000 aparecerán características que no se veían en el mapa anterior. Así, se ven ahora nuevas bahías y nuevas penínsulas. Si ahora examinamos de nuevo la costa, pero en un mapa que esté a una escala todavía más grande, digamos de 1/1 000, aparecerán unas bahías y penínsulas que no se veían en ninguno de los mapas anteriores. Así podemos continuar indefinidamente. Ahora bien, si comparamos cada uno de los mapas, de diferentes escalas, podemos darnos cuenta de que todos tienen la misma estructura. Es decir, la costa es también un fractal.

Figura 39. Dos puntos arbitrarios A y B a lo largo de una costa.
Analizaremos en seguida una propiedad inesperada de los fractales: supóngase que se quiere medir la longitud de la costa entre los dos puntos A y B (Figura 40, (a)). Una manera de hacerlo sería medir la longitud de la línea recta que une a A con B. Sin embargo, como se sabe, la costa es, en general, irregular, por lo que es claro que su longitud será mayor que la de la línea recta entre sus dos puntos extremos. Podríamos ahora tomar una unidad arbitraria de longitud H, por ejemplo una barra. Para medir la longitud de la costa llevaríamos esta barra a lo largo de ella (Figura 40, (b)) y contaríamos las veces que la barra cabe en la costa. A este número, denotado por L1, le llamamos la longitud de la costa. En seguida tomamos otra barra, de menor longitud, digamos H/l0 y repetimos el procedimiento obteniendo para la longitud el número L2. Podemos continuar indefinidamente de esta manera, tomando unidades cada vez más pequeñas. Intuitivamente esperaríamos que la sucesión de valores que se obtengan para las longitudes L1, L2, ... tendería a alcanzar un valor bien definido que sería la longitud de la costa. Sin embargo, esto no ocurre. De hecho lo que pasa es que esta sucesión de longitudes aumenta cada vez más y más. Es decir, al seguir el procedimiento indefinidamente, ¡la longitud de la costa entre A y B tiende a un valor infinito! Este resultado sorpresivo se debe precisamente al hecho de que al ir cambiando de escala van apareciendo más y más bahías y penínsulas pequeñas, cada una de estas contribuye a la longitud medida. Por muy chica que sea la nueva bahía o península, al ir aumentando la escala, en algún momento deberá ser tomada en cuenta y contribuirá a la longitud. Si uno cambiara el método de medición de la longitud, también llegaría a la misma conclusión.
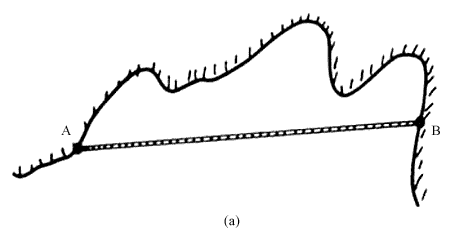
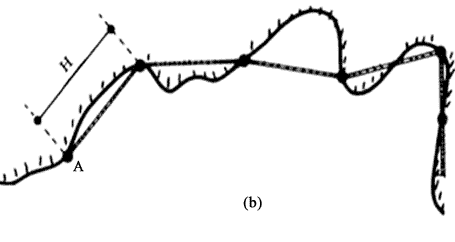
Figura 40. Procedimiento de medición de la longitud de la costa entre A y B.
Lo mismo sucedería si uno quisiera medir la longitud de la trayectoria que sigue la partícula browniana, mostrada en la figura 1. Su valor es infinito.
Otro ejemplo de fractal es la frontera entre dos países. Se puede dar un argumento análogo a los que hemos presentado y se llega a la misma conclusión. Por tanto, ¡la frontera entre dos países tiene, en rigor, longitud infinita!
Concluimos que una característica de los fractales es que al ser examinados con detalle, la longitud entre dos puntos fijos aumenta sin cesar al irnos a escalas cada vez menores.
En 1961 L. F. Richardson presentó una serie de mediciones experimentales que él hizo de varias costas, fronteras y cuerpos geométricos regulares. En cada caso fue cambiando la unidad de longitud H y obtuvo el correspondiente valor de la longitud L(H). En la figura 41 se muestran algunos de sus resultados. Se puede apreciar que al ir disminuyendo el valor de H la longitud L va aumentando. Sin embargo, se puede ver que la variación de L en ciertos intervalos de H no es muy pronunciada.
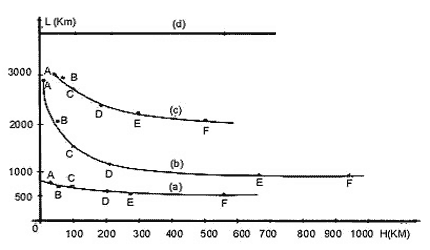
Figura 41. Valores de la longitud L de varias curvas al cambiar la longitud de la unidad de medida H, según L. F. Richardson. (a) Frontera entre Portugal y España. (b) Costa occidental de Gran Bretaña. (c) Frontera terrestre alemana (1900). (d) Perímetro de un círculo.
Podemos ahora preguntarnos lo siguiente: si aplicamos estas ideas a la medición del perímetro de una figura como un cuadrado o un círculo, ¿pasará lo mismo? En la figura 41 se ve que para un círculo el valor de L es constante (e igual al valor del perímetro del círculo, tal como se enseña en los cursos de geometría) en todo el intervalo de valores de H con el que se hicieron las mediciones. Lo que ocurre es que en las figuras geométricas, al aumentar la escala de observación, no aparecen nuevas estructuras que eran invisibles en la escala anterior ya que la línea que delimita a la figura no tiene estas estructuras. Por ejemplo, el círculo es, por definición, el conjunto de puntos que distan una longitud constante del centro. Por lo tanto, no puede haber algo análogo a la península en el caso de la costa.
En este punto esperamos que el lector se sienta incómodo. ¿Cómo es posible que, por ejemplo, la frontera entre dos países no esté perfectamente determinada? Pues, efectivamente, en lo que respecta a su longitud no lo está. Richardson menciona que cada uno de los países considera su valor dentro de la longitud de su frontera común. Por ejemplo, España dice que su frontera con Portugal mide 987 km, mientras que Portugal dice que son 1 214 km; Holanda dice que su frontera con Bélgica mide 380 km; mientras que Bélgica reclama que son 449 km. Lo que está sucediendo es que al hacer las mediciones, cada país utilizó, de hecho, diferente valor de la unidad de longitud H, y por tanto, obtuvo otro valor.
La discusión anterior nos lleva a la conclusión inesperada de que la longitud de objetos que son fractales no tiene un valor bien determinado. Esta longitud depende de la unidad H que se escoja. Si dos observadores eligen dos unidades distintas obtendrán dos resultados distintos. ¡Y ambos observadores tendrán razón! Es decir, este tipo de mediciones no es completamente "objetivo". Es claro que, en las relaciones entre países, se debe reconocer el carácter fractal de las cantidades que se van a medir y llegar a un convenio mutuo sobre cuál deberá ser la unidad de longitud que se debe seleccionar.
En términos matemáticos los resultados anteriores implican que a diferencia de las curvas unidimensionales, que supuestamente nos son familiares, los fractales son objetos que tienen dimensión mayor que uno; de hecho pueden tener dimensión cuyo valor está entre 1 y 2.
Se puede construir un tipo de figuras fractales siguiendo el ejemplo que a continuación se da. Tomemos un triángulo equilátero cualquiera (Figura 42, (a)), que se llama el iniciador. Divídase cada lado del triángulo en tres partes iguales. En la parte intermedia de cada lado añádase un triángulo equilátero que tenga su lado igual a una tercera parte del original. Se obtiene así la figura 42(b). En seguida, divídase otra vez cada uno de los lados de la figura así formada, en tres partes iguales, y en cada parte intermedia añádase un triángulo equilátero que tenga cada lado igual a la longitud resultante. Se encuentra así la forma mostrada en la figura 42(c). Si se continúa indefinidamente este procedimiento, se encuentra la forma de la figura 42(d). Ésta es un fractal y su perímetro tiene una longitud infinita.
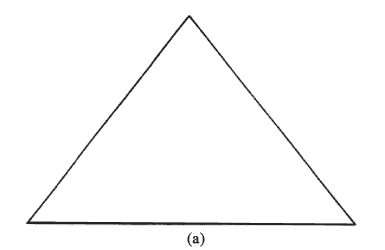
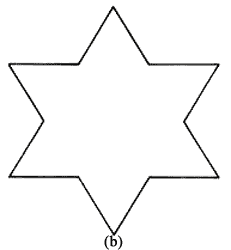
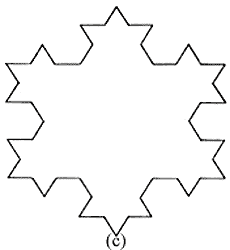

Analicemos con un poco de detalle el perímetro de estas figuras. Supongamos que el lado del triángulo iniciador de la figura 42 (a) sea 1; el perímetro del triángulo es entonces igual a 3. Por construcción, cada línea recta de la figura 42(b) tiene longitud (1/3). Por tanto, dado que hay 12 líneas rectas, el perímetro es 12 x (1/3) = 4. Cada línea recta de la figura 42c tiene longitud (1/9). En vista de que hay 48 de éstas líneas, este perímetro es 48)x(1/9) = 5.333.
Vemos entonces que la sucesión de valores de los perímetros es: 3, 4, 5.333, ... Esta sucesión va creciendo. La causa de que crezca es clara, ya que de un paso al otro el número de líneas rectas aumenta más rápidamente de lo que disminuye la longitud de cada línea recta. De hecho, en cada paso el número de líneas se multiplica por el factor 4, mientras que la longitud de cada línea disminuye 3 veces. Por lo tanto, el perímetro se multiplica, de un paso al otro, por el factor 4 x (1/3) = 1.333, que es un número mayor que 1. Si el número de pasos es infinito, el perímetro de la figura así formada también resulta ser infinito.
Mandelbrot ha argüido que en la naturaleza existen muchos fenómenos de carácter fractal, de hecho muchos más de los que nos imaginaríamos. Mencionaremos en forma breve algunos de ellos.
Además de las líneas costeras, los paisajes naturales también tienen características fractales. Así, la forma de cadenas montañosas da lugar a que al intentar medir su superficie, uno encuentre valores infinitos.
En la geometría usual se nos enseña que hay una relación determinada entre, por ejemplo, el área que ocupa una figura y la longitud del perímetro que encierra a dicha área. Esta relación es que la longitud del perímetro al cuadrado es proporcional al área encerrada. El coeficiente de proporcionalidad depende de la forma de la figura que se esté tratando. Así, por ejemplo, para un cuadrado, la longitud de su perímetro elevada al cuadrado es igual a seis veces el área encerrada. Para un círculo, la longitud del perímetro elevada al cuadrado es igual a cuatro veces p por el área encerrada.
Una relación análoga se encuentra entre el volumen de un cuerpo y el área de la superficie que lo encierra. En efecto, se demuestra que el cubo del área es proporcional al cuadrado del volumen encerrado, dependiendo el coeficiente de proporcionalidad de la figura de que se trate.
Si ahora se considera, por ejemplo, el caso de los cerebros de los mamíferos, se sabe que su corteza tiene muchas circumvoluciones. Resulta de mediciones hechas con mucha precisión que la relación entre el volumen del cerebro y el área de la superficie que lo encierra no sigue el patrón arriba dado para figuras geométricas. Se encuentra que el cubo del área es proporcional no al volumen elevado al cuadrado, sino al volumen elevado a una potencia que varía entre 2.73 y 2.79. Se puede demostrar que este resultado implica que la superficie que encierra al cerebro es fractal. Esto se ha explicado en términos de las necesidades de la evolución de los mamíferos.
Otro ejemplo biológico ocurre en la estructura nasal de algunos animales. La membrana que cubre el hueso de la nariz es tal que la relación entre área y volumen encerrado no sigue un patrón geométrico, sino fractal. Ciertos animales tienen un área muy grande para el volumen que encierran. Esta membrana podría estar relacionada con el sentido del olfato, y por ejemplo en el caso de los camellos, su gran área les ayudaría para localizar, husmeando, el agua que es muy escasa en los desiertos.
La descarga y el nivel de las crecidas de los ríos son otro ejemplo de fractales. Resulta que estas cantidades, tomadas anualmente, tienen valores muy persistentes. Se han intentado dar, infructuosamente, diversas explicaciones de este hecho. Aparentemente, la única que tiene visos de conformarse con los resultados experimentales es que estas cantidades se comportan como fractales.
También se han aplicado las ideas de los fractales en economía. Un análisis detallado del comportamiento de los cambios de precios de los productos muestra que tienen una estructura análoga a la de un fractal. Esto se debe que al cambiar de escalas temporales en la determinación de estos cambios, se encuentran estructuras análogas.
En lingüística también aparecen estructuras fractales. Se han estudiado las relaciones que, en un idioma determinado, sigue la frecuencia de uso de palabras. Pues resulta que este comportamiento es fractal. Uno de los parámetros de este fractal da la medida de qué tan rico es el uso del vocabulario a través de la frecuencia relativa del uso de palabras raras.
Se ha podido determinar que los fractales también aparecen en la teoría de circuitos eléctricos y en la teoría de la información, por mencionar sólo algunos campos. Se han abierto de esta manera vastos horizontes de estudio y aplicación que apenas han empezado a explotarse.