III. SIGUE LA HISTORIA: EINSTEIN

EN EL año de 1905 el famoso físico Albert Einstein (1879-1955) publicó un célebre trabajo en el que propuso la explicación del movimiento browniano. Es interesante notar que ese mismo año Einstein publicó otros dos famosos trabajos: el del efecto fotoeléctrico (que le valdría el premio Nobel de Física en 1923) y el de la teoría de la relatividad.

Para apreciar la contribución de Einstein hay que mencionar que hasta ese momento todos los argumentos propuestos para el movimiento browniano habían sido sólo cualitativos. Es decir, no se había formulado ninguna teoría de la que se pudiera colegir relación alguna que fuera susceptible de medirse experimentalmente.

En su trabajo, Einstein contrastó las predicciones de las leyes de la termodinámica con las de la teoría cinética, que estaba basada en la suposición atómica. En particular se interesó por las conclusiones que se obtendrían si el movimiento browniano se tratara de explicar por medio de la hipótesis atómica.

Un escollo importante fue la objeción hecha por Nñgeli, que ya mencionamos antes, acerca de la posibilidad de que el movimiento browniano se pudiera explicar como efecto de las colisiones entre la partícula browniana y los atómos que componen el fluido. Se hizo ver que el argumento de Nñgeli no era correcto. En efecto, en primer lugar, según había mostrado Maxwell, las partículas del fluido no tenían todas la misma velocidad, sino que tenían muchas velocidades; es decir, tenían una distribución de velocidades. Además, estas velocidades tienen todas las posibles direcciones (Figura 3). En segundo lugar, el número de colisiones que experimenta una partícula en un fluido es extraordinariamente grande, del orden de ñ10²⁰ (un uno seguido de veinte ceros) colisiones en cada segundo! Entonces, y a pesar de que en cada colisión con un átomo del fluido una partícula suspendida en él cambia su velocidad en una cantidad extremadamente pequeña (tal y como lo calculó Nñgeli), puesto que la partícula suspendida experimenta un número extraordinariamente grande de colisiones, el efecto acumulado de todas las colisiones resulta ser apreciable.

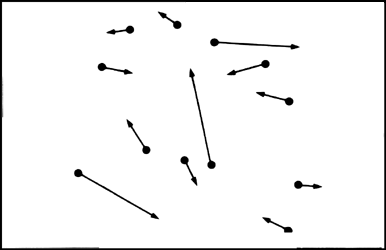
Figura 3. Las velocidades de los átomos de un fluido tienen todos las posibles direcciones y sentidos.

Otra objeción que se resolvió fue la siguiente: si las partículas del fluido chocan por todos lados con la partícula suspendida puede ocurrir que dos de ellas choquen en forma opuesta (Figura 4) de tal manera que el pequeño efecto que cada una de ellas hace sobre la partícula suspendida se cancele. Sin embargo, dado que es altamente improbable que dos partículas del fluido que chocan en sentidos diametralmente opuestos con la suspendida tengan justamente las mismas magnitudes de sus velocidades, esta cancelación de efectos no ocurre.

Figura 4. Es poco probable que en un instante dado dos partículas del fluido choquen con la browniana en forma diametralmente opuesta y tengan justamente las mismas magnitudes de sus velocidades.

Está claro entonces que el resultado neto es que la partícula suspendida experimenta un cambio finito de velocidad y que su dirección también se altera. Estos cambios son impredecibles tanto en magnitud como en dirección ya que dada la cantidad de colisiones, no es posible seguir el efecto individual de cada una de ellas. Pero lo importante es que éstas ocurren continuamente, por lo que la partícula suspendida cambiará su velocidad también en forma continua, tanto en magnitud como en dirección. De este modo, la partícula browniana realiza un movimiento fluctuante, azaroso, en zigzag como el mostrado en la figura 1. Nos damos cuenta de que este movimiento debe llevarse a cabo todo el tiempo mientras el sistema exista. Como se vio arriba, Cantoni y Oehl ya habían encontrado experimentalmente este resultado.

Un antecedente de mucha relevancia que hay que mencionar en este momento es que desde el año de 1902 Einstein había trabajado en la teoría microscópica de la termodinámica, teoría que en la actualidad recibe el nombre de mecánica estadística. En el transcurso de estas investigaciones, Einstein se vio en la necesidad de estudiar las fluctuaciones que ocurren en las cantidades termodinámicas alrededor de sus valores de equilibrio. Una vez que pudo establecer con claridad las características de estas fluctuaciones se interesó en aplicar las ideas que desarrolló a otros fenómenos físicos que involucraran también fluctuaciones. Éste fue uno de los motivos por los que se interesó en el movimiento browniano. Otro campo en el que aplicó sus ideas sobre fluctuaciones fue el de la radiación de cuerpo negro; de ahí surgio su famoso trabajo sobre el efecto fotoeléctrico.

Regresando al tema del movimiento browniano, Einstein obtuvo además de conclusiones cualitativas predicciones cuantitativas que podrían compararse con resultados experimentales. Entre estas predicciones destacan dos muy importantes: predijo la distancia que debe recorrer una partícula suspendida en un fluido y además, mostró que la segunda ley de la termodinámica se cumple sólo en promedio. Supongamos que en el instante inicial la partícula suspendida está en cierto punto, digamos en A (Figura 5,(a)). Después de cierto tiempo t, la partícula se encontrará en B, que está a una distancia d del punto inicial A. Si se repite esta experiencia, resulta que la partícula en el mismo tiempo t no se encontrará ahora a una distancia d como antes, sino a otra distancia, digamos d_<1 (Figura 5(b)). Si se vuelve a repetir la experiencia, en lugar de d₁ se encontrará otra distancia, digamos d₂ (Figura 5(c)), y así sucesivamente. Se pueden tomar los cuadrados de estas distancias encontradas en una sucesión muy grande de experiencias y calcular el promedio de estos cuadrados. Denotaremos este promedio como <d²> y lo llamaremos desplazamiento cuadrático medio. Einstein predijo que esta cantidad debe comportarse, según transcurre el tiempo, en la forma mostrada en la figura 6. Esta curva tiene dos secciones. La primera de ellas, que va de O a N, o sea entre el tiempo inicial y un tiempo que llamamos t es una parábola. Para tiempos mayores que t, la gráfica es una línea recta, que corresponde a la sección NM. El tiempo es un tiempo extremadamente corto. Ahora bien, en mecánica se demuestra que el hecho de que la curva sea una parábola nos indica que en el intervalo entre O y t la partícula suspendida se comporta como una partícula libre. Esto se desprende del siguiente argumento. Al colocar la partícula en el fluido, mientras no choque con ninguna de las partículas del fluido, se comportará como partícula libre. Es obvio que este intervalo dura muy poco tiempo. Una vez que empieza a chocar con las partículas del fluido, entonces, según Einstein, la gráfica cambia y debe ser una línea recta. Resulta de la hidrodinámica que un comportamiento rectilíneo de este tipo corresponde a la difusión de la partícula en el fluido. Einstein encontró, además, que la inclinación de la recta depende de varias cantidades: la temperatura del fluido, su viscosidad, las dimensiones de la partícula y el número de Avogadro. Recordemos que éste es el número de átomos que contiene un mol de sustancia.

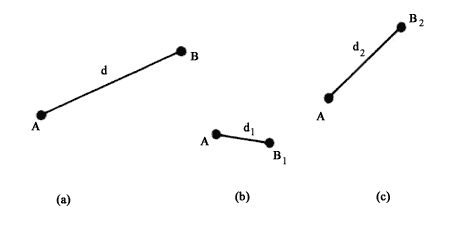
Figura 5. Al realizar repetidas veces la observación del movimiento de partículas brownianas que inicialmente están en el mismo punto (A), se encontrará que al final del mismo intervalo se hallan a distintas distancias de su posición inicial.

Por otro lado, Einstein hizo ver además, que en el caso del movimiento browniano efectivamente se violaba la segunda ley de la termodinámica, y no porque esta ley no fuera correcta, sino porque no se la podía interpretar de la manera absoluta en que los energeticistas lo hacían. De hecho había que darle una interpretación estadística: la segunda ley se cumple solamente en promedio.

De esta forma, Einstein planteó un problema al que solamente la naturaleza, a través de un experimento, podría dar solución: la posibilidad de medir el desplazamiento cuadrático medio de una partícula browniana.

Fue el físico Jean Perrin, con ayuda de su discípulo M. Chaudesaigues, quien entre los años 1908-1911 realizó este experimento. Describiremos brevemente la manera en que lo hiciera. En primer lugar, hay que darse cuenta de que no es posible registrar la posición exacta de una partícula browniana. Al ser observada en un ultramicroscopio, una partícula de éstas se manifiesta como un destello luminoso. Debido al tipo de movimiento que realiza, este destello parece vibrar alrededor de una posición promedio. Fue V. Henri quien introdujo el método de observar este movimiento por medio de una serie de fotografías tomadas por una cámara cuyo ojo se abría en intervalos de 0.05 s y con exposiciones de 0.003 s. Lo que hizo Perrin fue tomar una serie de estas fotografías, registrando las posiciones de la partícula en intervalos de 30 s. Así obtuvo algo análogo a lo mostrado en la figura 1. Graficó luego los valores cuadráticos medios y obtuvo que, efectivamente, a partir de cierto instante, su gráfica era una línea recta. Además, pudo medir la inclinación de esta recta, y dado que conocía la temperatura y la viscosidad del fluido así como las dimensiones de la partícula, dedujo de la fórmula de Einstein que el valor del número de Avogadro debería ser igual a 6.4 X 10²³. Este valor concordaba con los obtenidos por otros métodos completamente independientes, como la electrólisis, el experimento de Millikan para encontrar la razón de la carga a la masa del electrón, la separación reticular en un cristal, y otros más. El valor del número de Avogadro, medido en la actualidad con mucha mayor precisión, es 6.02 x 10²³. Por sus estudios sobre el movimiento browniano Jean Perrin recibió el premio Nobel de Física en 1926.

La predicción de la línea recta que aparece en la figura 6 y el valor del número de Avogadro fueron también el resultado del trabajo de otros científicos, entre los que solamente citaremos a M. Seddig (1908), V. Henri (1908), T. Svedberg (1906-1912), F. Ehrenhaft (1907), M. de Broglie (1909), H. Fletcher (1911).

Después de esta brillante confirmación del trabajo de Einstein, y para ser más precisos, de las hipótesis que formuló, quedaron muy pocas dudas sobre la realidad de la estructura atómica de la materia. Así, por ejemplo, S. Arrhenius dijo lo siguiente en una conferencia que dictó en París en 1911: "Después de esto, no es posible dudar que la teoría atómica considerada por los filósofos de la antigñedad, Leucipo y Demócrito, haya alcanzado la verdad, por lo menos en su parte esencial."

Fue Ostwald, uno de los impugnadores de la teoría atómica, quien en 1909 escribió en el prefacio de su libro Grundriss der allgemeinen Chemie: "Me he convencido de que hemos entrado recientemente en posesión de la prueba experimental de la naturaleza discreta de la materia, que la hipótesis atómica había buscado en vano durante siglos, por no decir milenios." Es decir, todos estos trabajos convencieron a Ostwald. Sin embargo, Ernst Mach, otro de los opositores, no cambió su opinión. De hecho, él fue prácticamente el único científico que no aceptó la hipótesis atómica por lo que se quedó solo.

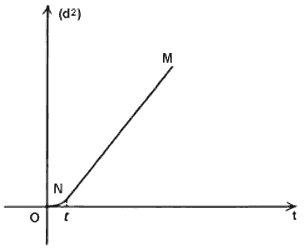
Figura 6. El desplazamiento cuadrático medio de la partícula browniana predicho por Einstein.

A partir de entonces se consolidó para siempre esta hipótesis y ya nadie ha vuelto a dudar de ella. Asimismo, quedaron claros los límites para entender la segunda ley de la termodinámica.

Se podría pensar que una vez explicado el movimiento browniano por el trabajo de Einstein ya no había nada que hacer en este campo. Sin embargo, esto no es cierto. La importancia del movimiento browniano dejó de residir en la explicación de sus causas o en la confirmación de la hipótesis atómica, adquiriendo un renovado interés por otras posibilidades que ofreció. Solamente mencionaremos algunas de ellas: dar luz en el campo de los procesos irreversibles; impulsar al campo de las matemáticas que estudia las llamadas funciones no-diferenciables; aplicaciones en la teoría de suspensiones coloidales; utilización de estas ideas en otros campos, como el de los láseres; abrir sorprendentes horizontes en el desarrollo de la teoría de los fractales, y varias más.