V. ¿QUÉ ES EMPÍRICO Y QUÉ ES MICROSCÓPICO

EN EL capítulo anterior se habló de algunos procesos irreversibles. El problema ahora es cómo describirlos. En primer lugar, debemos saber cuáles son las cantidades importantes en cada uno de estos procesos. Una vez que se ha decidido esta cuestión surge otra, a saber, ¿qué relación existe entre las diferentes cantidades importantes?

Para aclarar lo anterior veamos un ejemplo. Consideremos el caso en que se ponen en contacto dos cuerpos que inicialmente tienen temperaturas distintas. Se sabe que la temperatura de cada cuerpo empieza a cambiar. Uno puede preguntarse qué valor tienen las temperaturas de cada uno de los cuerpos desde que se les pone en contacto. Para determinarlo colocamos un termómetro en cada cuerpo y medimos su temperatura a intervalos regulares. De esta manera se puede construir la gráfica de la temperatura de cada cuerpo como función del tiempo. Si se hiciese este experimento se encontrarían gráficas del tipo mostrado en la figura 8. Aquí T₁ y T₂ son las temperaturas que tenían los cuerpos inicialmente. Se ha supuesto que la temperatura T₂ es mayor que la temperatura T₁ . Al transcurrir el tiempo, el cuerpo que inicialmente estaba caliente se enfría (curva superior en la figura 8), es decir, su temperatura disminuye. El cuerpo que inicialmente estaba frío se calienta, por lo que su temperatura aumenta (curva inferior en la figura 8). Después de un cierto tiempo q, los dos cuerpos alcanzan la misma temperatura T, que luego cada uno mantiene indefinidamente.

Ahora bien, ¿qué cantidades son las importantes en el desarrollo temporal de este proceso? Esta respuesta se ha encontrado después de mucha actividad experimental. No entraremos en detalles, solamente daremos el resultado. Tomemos, por ejemplo, el instante de tiempo t (véase la Figura. 9). En este instante las temperaturas de los cuerpos son T₁ (t) y T₂ (t), respectivamente. Resulta que si entre los dos cuerpos existe una diferencia de temperatura, entonces hay un flujo de calor del más caliente al más frío. El flujo de calor es proporcional a la diferencia de temperaturas entre los cuerpos. En particular, en el instante t, el flujo de calor es proporcional a la diferencia T₁ (t) - T₂ (t). Así, en el instante inicial esta diferencia de temperaturas es igual a AB (ver Fig. 9), mientras que en el instante t es igual a CD, menor que AB. En un instante posterior, t', esta diferencia de temperaturas es igual a FG, que es más pequeña aún. Esto significa que inicialmente hay un flujo de calor entre los cuerpos que es proporcional a AB. Al transcurrir el tiempo, este flujo de calor va disminuyendo de manera continua. Así, después del tiempo q y dado que las diferencias de temperaturas son prácticamente nulas, ya no hay flujo de calor entre los cuerpos y, por tanto, ya no se modifican sus temperaturas: se ha llegado al estado de equilibrio.

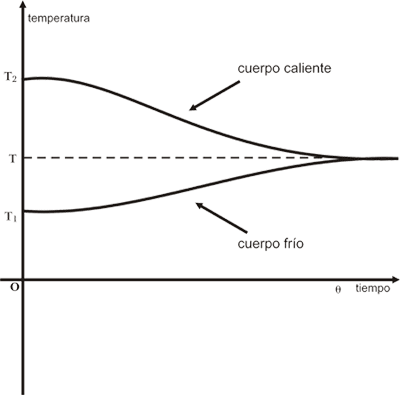
Figura 8. Variación de las temperaturas de dos cuerpos en contacto al transcurrir el tiempo. Inicialmente están a distintas temperaturas.

Se ha descubierto por la experiencia que uno de los factores importantes en la evolución de este fenómeno es la diferencia de temperaturas entre los cuerpos en contacto. Nótese que, por sí solos, los valores de cada una de las temperaturas de los cuerpos carecen de importancia, solamente su diferencia es significativa.

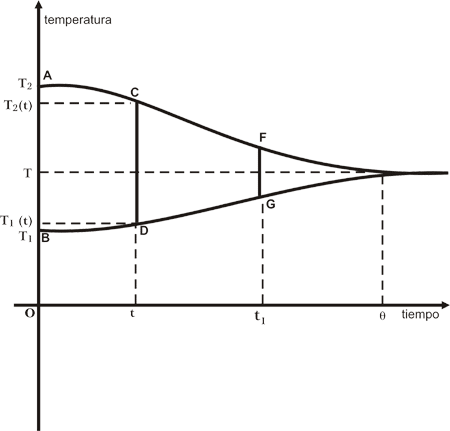
Figura 9. En cada instante el flujo de calor del cuerpo caliente al frío solamente depende de la diferencia de las temperaturas entre ellos.

¿Es éste el único factor importante? No: aun con la misma diferencia de temperaturas entre los cuerpos, no resulta lo mismo si se pone en contacto cobre con aluminio que si se trata de cobre con madera. Para la primera pareja de cuerpos se alcanza el estado de equilibrio en un tiempo q mucho más pequeño que para la segunda pareja es decir, los tiempos de relajación en los casos son distintos. Ahora bien, la diferencia entre estos dos casos es que se cambió el aluminio por la madera.

El aluminio se diferencia, entre otras cosas, de la madera, por el hecho de que su capacidad de hacer pasar el calor es mayor que la de este material. Se dice que la conductividad térmica del aluminio es mayor que la de la madera. Pues bien, mientras mayor sea la conductividad térmica de una de las sustancias que se ponen en contacto, más pequeño será el tiempo de relajación y, por tanto, se llegará más rápidamente al estado de equilibrio.

Existe además otro factor que influye en el fenómeno. Este factor es la capacidad del cuerpo frío de absorber el flujo de calor, y la capacidad del cuerpo caliente de emitir o soltar el flujo de calor. Esta cantidad se llama capacidad calorífica del cuerpo. Mientras más grande sea la capacidad calorífica de un cuerpo más fácilmente absorberá (o emitirá) la energía calorífica y más pronto se establecerá el estado de equilibrio. Por tanto, el tiempo de relajación también depende de esta capacidad.

Sintetizando: en el ejemplo que acabamos de dar, los factores importantes para la descripción del proceso irreversible son la diferencia de temperaturas entre los cuerpos, sus conductividades térmicas y sus capacidades caloríficas. En general, dados dos cuerpos que se van a poner en contacto, es necesario hacer experimentos para medir el valor de cada una de estas propiedades.

Debemos notar que en la descripción que se acaba de hacer del proceso irreversible nunca se tuvo que mencionar que cada uno de los cuerpos que se ponían en contacto estuviese compuesto de átomos. De hecho, las diferencias entre ellos solamente se manifestaron a través de características como la conductividad térmica y la capacidad calorífica y nada más. A este tipo de descripción se le llama empírica, fenomenológica o macroscópica.

Sin embargo, se sabe que los cuerpos están compuestos de átomos o moléculas. Por tanto, uno esperaría que también se pudiera describir este proceso irreversible en términos de las propiedades atómicas de las sustancias en contacto. Este tipo de descripción se llama microscópico, e implica que el conocimiento de las leyes microscópicas que rigen los movimientos de los átomos debería llevarnos, de alguna manera, a determinar el comportamiento macroscópico de la sustancia. En particular, se debería poder justificar cuándo y bajo qué circunstancias son válidas las leyes de la termodinámica de las que hablamos en secciones anteriores; además, deberíamos ser capaces de predecir cuánto valen las diversas propiedades de las sustancias como su conductividad térmica, su capacidad calorífica, etcétera.

Hemos de mencionar que este problema, planteado tal y como lo acabamos de hacer, no ha sido resuelto hasta el día de hoy en forma general. Solamente para algunos sistemas sencillos, como gases a muy baja densidad, cristales perfectos o algunos sistemas magnéticos, se ha podido llevar a cabo, en parte, este ambicioso programa. Para sistemas más complicados el programa no se ha cumplido. Una de las principales dificultades estriba en que si se considera una sustancia macroscópica, ésta tiene alrededor de 10²⁰ (ñun uno seguido de veinte ceros!) átomos en cada centímetro cúbico de volumen. En consecuencia, para describir su evolución y sus propiedades se requiere conocer la trayectoria que describe cada uno de sus átomos. A este problema se le llama en física el "problema de muchos cuerpos". Para fuerzas reales entre los átomos su solución rigurosa no se ha obtenido aún. Cabe hacer notar que en forma exacta se ha resuelto solamente el problema de dos (sí, dos) cuerpos. El problema de tres cuerpos solamente ha sido resuelto en forma aproximada. Si por algún motivo las fuerzas que se ejercen entre las partículas de un sistema son muy débiles, entonces se puede seguir con bastante precisión el programa arriba indicado. Esto es justamente lo que ocurre en los sistemas que se mencionaron antes, como los gases densos, etcétera.

Aprovecharemos la oportunidad para mencionar que este tipo de problemas de muchos cuerpos se presenta en varios campos de la física, como por ejemplo en la física atómica, en donde se trata de describir las propiedades de un átomo que está compuesto de varias partículas (núcleo y nube de electrones que lo rodea). Solamente ha sido resuelto rigurosamente el caso del átomo de hidrógeno, formado por un núcleo y un solo electrón, es decir, se trata de un problema de dos cuerpos. Otros átomos han sido estudiados sólo en forma aproximada. Otro campo en donde tiene importancia el problema de muchos cuerpos es en la astronomía, en que se trata de describir los movimientos de varios cuerpos celestes, unos en presencia de otros. Por ejemplo, el caso del Sol, la Tierra y la Luna solamente ha sido resuelto en forma aproximada (aunque con una precisión muy alta). Finalmente, mencionaremos otro campo, el de la física nuclear, en donde se trata de entender él comportamiento del núcleo de un átomo, que está compuesto de varias decenas de partículas (protones y neutrones).

El movimiento de una partícula browniana inmersa dentro de un fluido proporciona un caso en el que sí es posible hacer una descripción dentro de los lineamientos arriba mencionados. En efecto, debido a la gran diferencia entre la masa de la partícula browniana y las masas de las partículas que componen el fluido,* resulta que es posible reducir su descripción a la del movimiento de un solo cuerpo. En ciertas condiciones, es ya posible resolver el problema y de esta manera estudiar con gran detalle la evolución irreversible del cuerpo hacia su estado de equilibrio.

Como ocurre con mucha frecuencia, se dispone de la descripción microscópica de un fenómeno. Es a partir de ello que se encuentran distintas consecuencias sobre el comportamiento del sistema en cuestión. Al hacer la descripción macroscópica, uno se contenta solamente con justificar las propiedades y leyes macroscópicas del sistema, dado que las consecuencias macroscópicas ya se han encontrado. Por lo tanto, antes de intentar hacer una descripción microscópica conviene conocer la macroscópica; es decir, saber hacia dónde encaminar los pasos, o en otras palabras, saber qué es lo que hay que justificar.

En vista de lo anterior, revisaremos en los siguientes capítulos el fenómeno del movimiento browniano desde el punto de vista de los procesos irreversibles. En primer lugar haremos una exposición macroscópica del fenómeno y posteriormente se estudiará la manera en que se ha justificado microscópicamente.

NOTAS

* La masa de la partícula browniana es muy grande comparada con la de los átomos, pero muy pequeña desde el punto de vista macroscópico.