VI. DESCRIPCIÓN EMPÍRICA DEL MOVIMIENTO BROWNIANO. ESTADÍSTICA
UNA de las primeras descripciones macroscópicas del movimiento browniano fue hecha en 1908 por el físico francés Paul Langevin. Él hizo las siguientes consideraciones: si una partícula grande (comparada con las dimensiones atómicas) se introduce en un fluido, entonces, de acuerdo con la hidrodinámica, va a experimentar una fuerza opuesta que depende de su velocidad. Como ejemplo de este hecho podemos mencionar el caso de un auto o de un aeroplano que se mueven: el aire genera una fuerza que se opone al movimiento; o cuando nadamos en una alberca: el agua se opone a nuestro movimiento. Esta fuerza de oposición se debe a la viscosidad del fluido. Mientras mayor sea la velocidad con que se mueve el cuerpo dentro del fluido, mayor será la fuerza de oposición, o de fricción viscosa, que se genere.
Por otro lado, de lo descrito anteriormente se sabe que al introducir una partícula grande dentro de un fluido, aquélla experimenta fuerzas debidas a las colisiones que sufre con las moléculas del fluido. En vista de la gran cantidad de colisiones que ocurren en cada instante, esta segunda fuerza varía de una forma muy azarosa y violenta. Ello significa que si, por ejemplo, hacemos observaciones de la partícula browniana con una escala de tiempo del orden de los segundos la fuerza debida a las colisiones variará mucho, pues en un segundo habrán ocurrido muchísimas colisiones. Por otro lado, en esta misma escala de tiempo, la primera fuerza de la que hemos hablado, la de fricción, varía muy poco (Figura 10).
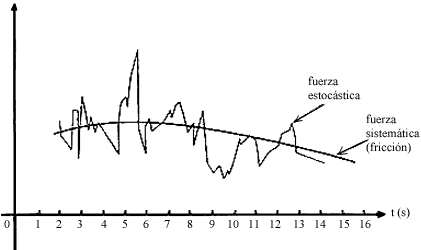
Figura 10. Las fuerzas estocástica y viscosa que experimenta la partícula browniana varían en diferentes escalas de tiempo.
De esta manera, se reconocen dos escalas de tiempo muy distintas: la escala en la que varía la fuerza de fricción (que es, para casos típicos, del orden de segundos) y la escala en la que varía la fuerza debida a las colisiones (que es del orden de milésimas de microsegundo). Esto significa que si observamos los fenómenos con escalas de tiempo de segundos, la fuerza de fricción apenas cambia, mientras que la otra fuerza ya habrá cambiado muchísimas veces.
Ahora bien, si se conoce la velocidad de la partícula, la fuerza de fricción también se puede determinar: es proporcional a ella. Es decir, si la velocidad aumenta al doble, la fuerza se duplica; si la velocidad se triplica la fuerza aumenta al triple, etcétera. El coeficiente de proporcionalidad entre la fuerza y la velocidad depende de la viscosidad del fluido así como de la forma geométrica de la partícula. Estas dependencias son conocidas aunque no las daremos aquí. Además, el sentido que tiene la fuerza es opuesto al de la velocidad ya que aquélla se opone al movimiento (Figura 11). En otras palabras, es posible determinar completamente esta fuerza en cada instante. En la teoría del movimiento browniano se suele llamar fuerza sistemática a esta fuerza de fricción.
Otra cosa ocurre con la fuerza debida a las colisiones. Dado que en un segundo el número de colisiones que experimenta la partícula browniana con las del fluido es enorme, resulta prácticamente imposible determinar el valor exacto de esta fuerza en cualquier instante. Por la misma causa, este valor varía en pequeños intervalos, de manera impredecible. Estamos entonces ante una situación en que una de las fuerzas que experimenta la partícula browniana varía de manera azarosa; es decir, se tiene una fuerza fluctuante. En matemáticas este tipo de cantidad recibe el nombre de estocástica.
Figura 11. La fuerza viscosa tiene sentido opuesto a la velocidad de la partícula.
Antes de continuar, haremos un breve paréntesis para hablar acerca de algunas propiedades importantes de las cantidades estocásticas. La parte de las matemáticas que trata de ellas es la estadística.
Consideremos el caso de una fábrica que produce clavos de 20 cm de largo. Resulta que si medimos con cuidado las longitudes de los clavos fabricados, nos daremos cuenta de que no todos los clavos son de 20 cm. Los hay de 20.01 cm, de 19.99 cm, de 20.02 cm, etcétera. Por muy alto que sea el nivel del control de calidad, siempre se producirán clavos de distintas longitudes. Esto, en general se debe a una multitud de causas que son muy difíciles, o a veces imposibles de controlar. Por ejemplo, una pequeña variación en la temperatura del ambiente puede ser causa de que la longitud de los clavos fabricados cambie. Esto tiene como consecuencia que los clavos producidos no tengan todos la misma longitud. De un lote, habrá cierto número de clavos con longitud de 20 cm, otros de 20.01 cm, otro número de clavos con 19.99 cm, etcétera. Por tanto, la longitud de los clavos es una cantidad estocástica. En consecuencia, se genera así una distribución de las longitudes de los clavos. En la figura 12 se muestra una gráfica de esta distribución. La gráfica nos indica el número de clavos que hay con determinada longitud. Vemos que la mayoría de ellos se encuentra alrededor de 20 cm. Sin embargo los hay, aunque muy pocos, de longitudes que varían bastante de 20 cm. Vemos que mientras mayor sea la variación de la longitud con respecto a 20 cm, menor será el número de clavos que haya con estas dimensiones.
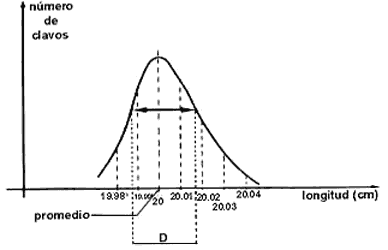
Figura 12. La distribución de las longitudes de una muestra de clavos.
Sin embargo, lo que sí se quiere garantizar es, por lo menos, que de un lote de clavos producidos, el promedio de sus longitudes sea de 20 cm (Figura 12). Una vez que reconocemos lo anterior, sería deseable que la mayoría de los clavos tuvieran longitudes alrededor de 20 cm, separándose muy poco, de este valor. Es decir, desearíamos que casi no hubiera clavos con longitudes de, por ejemplo, 22 cm. Ello significa, si nos referimos a la figura 12, que el ancho D de la curva de la distribución será muy pequeño. Así, consideremos las dos distribuciones mostradas en la figura l3. Vemos que ambas dan el mismo promedio. Sin embargo, en una de ellas, la más ancha, sí hay un número apreciable de clavos que tienen longitudes que varían mucho de 20 cm, mientras que en la otra, la angosta, casi no hay clavos cuya longitud se aleja mucho de 20 cm. Diríamos que el control de calidad de los clavos asociado a la curva angosta es mejor que el asociado al otro lote. El ancho D de cualquiera de estas distribuciones se llama la desviación estándar de la distribución. Esta cantidad está asociada al promedio de los cuadrados de la longitud, es decir, a su valor cuadrático medio.
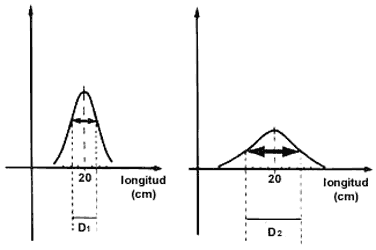
Figura 13. Dos distribuciones distintas que tienen el mismo promedio (20 cm) pero desviaciones estándar distintas.
Si el número de clavos producidos es muy grande, resulta que la distribución tiene, en general, una forma de campana, como la mostrada en la figura 12. A este tipo de distribución se le llama gaussiana o normal. Se puede demostrar en matemáticas que una distribución gaussiana queda completamente determinada si se conocen su promedio y su desviación estándar.
En general, si uno está tratando con cantidades estocásticas, su descripción se hace en términos de su distribución. Dos características que tiene la distribución son las anteriormente mencionadas: su promedio y su desviación estándar.
Regresemos ahora al caso del movimiento browniano. Una de las fuerzas que experimenta la partícula es, como se explicó arriba, estocástica. Por tanto, se tiene que decir algo acerca de su distribución. Además hay que tener en mente que esta fuerza estocástica cambia al transcurrir el tiempo, lo que significa que no sólo hay que decir algo acerca de su distribución en un instante dado de tiempo, sino también algo acerca de cómo están relacionados los valores de las fuerzas estocásticas en distintos instantes.
Langevin formuló la hipótesis, que de hecho es la más sencilla, de que la distribución de la fuerza estocástica es gaussiana. Por tanto, su determinación se reduce a conocer su promedio y su desviación estándar.
Promedio: En estas fuerzas fluctuantes, sería razonable pensar que si tomamos un intervalo de, por ejemplo, un segundo, se ejerciesen fuerzas en un sentido y en el sentido opuesto (Figura 14) de forma tal que, en promedio, la fuerza ejercida se cancelara. Se supone entonces que en cada instante el promedio de la fuerza estocástica es nulo.
Figura 14. Fuerzas estocásticas que experimenta la partícula browniana es un intervalo de segundos. El promedio de estas fuerzas es nulo.
Desviación estándar: Si hacemos observaciones en escalas del orden de segundos, como se acostumbra en el laboratorio, entonces el valor de la fuerza estocástica en un instante dado no tiene nada qué ver con el valor que adquiere la fuerza en otro instante que esté separado por segundos del primero. Esto se debe a que en un segundo la fuerza varió muchísimo, de tal manera que al final del intervalo la fuerza no tiene una relación estrecha con el valor que tenía al principio del intervalo. Se dice que las fuerzas estocásticas o fluctuantes no están correlacionadas entre sí en distintos instantes de tiempo.
En resumen, de estos razonamientos concluimos que la fuerza total que experimenta la partícula browniana es la suma de dos fuerzas: la sistemática y la estocástica. La fuerza estocástica varía mucho en la escala de tiempos en que cambia la fuerza sistemática. Ahora bien, si se suman dos cantidades, una de ellas conocida, pero la otra de naturaleza estocástica, la suma también va a ser estocástica. En consecuencia, la fuerza total que experimenta la partícula es estocástica.
Por otro lado, de acuerdo con los principios de la mecánica desarrollados por Newton, la fuerza que experimenta una partícula determina la trayectoria y la velocidad que tiene. Ello significa que, en nuestro caso, si la fuerza aplicada es estocástica, tanto la posición como la velocidad de la partícula son también cantidades estocásticas. En consecuencia, la solución del problema radica en poder determinar las distribuciones tanto de la posición como de la velocidad de la partícula, ya que en estas circunstancias no hay manera de determinar los valores precisos de la posición y de la velocidad en cada instante. En el mejor de los casos solamente se podrán determinar sus distribuciones.
Este problema se resuelve introduciendo en el fluido la partícula con una velocidad bien determinada de magnitud, digamos, v0 . El resultado que se encuentra es que en cada instante tanto la velocidad como la posición de la partícula se definen en términos de distribuciones que también son gaussianas.
Consideremos primero los resultados para la velocidad y luego para la posición: se encuentra que el promedio de la velocidad se comporta como se muestra en la figura 15. Aquí v0 es el valor que tiene inicialmente la partícula. Vemos que al transcurrir el tiempo el promedio del valor de la velocidad va disminuyendo hasta que finalmente adquiere el valor de cero. Esto significa que la partícula llega a "olvidar" el valor inicial de su velocidad. El tiempo t que la velocidad tarda en llegar a un valor pequeño, comparado con el inicial, se llama otra vez tiempo de relajación. Este tiempo t depende de la viscosidad del fluido. Mientras más viscoso sea el fluido más pequeño será el tiempo t. Es decir, mientras más viscoso sea el fluido, más rápidamente "olvidará" la partícula su velocidad inicial. El hecho de que el promedio sea nulo significa que la partícula puede tener velocidades tanto en un sentido como en el opuesto.
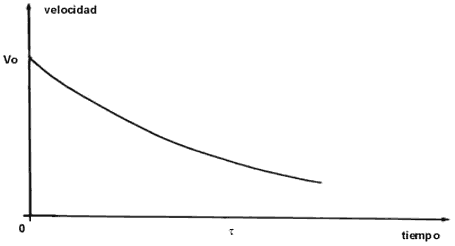
Figura 15. Promedio de la velocidad de la partícula browniana al transcurrir el tiempo, si inicialmente tenía el valor v0.
La desviación estándar de la velocidad esta relacionada con su valor cuadrático medio. Esta última cantidad se comporta según se muestra en la figura 16. Inicialmente este valor es nulo. Esto se debe a que inicialmente se tiene la certeza de que la velocidad es justamente v0 . Otra manera de decirlo es que inicialmente la distribución de la velocidad tiene un ancho nulo. Al transcurrir el tiempo, el ancho de la distribución de velocidades va aumentando, hasta que después de un tiempo t adquiere un valor constante. Este valor constante no depende de las condiciones iniciales. Nuevamente, esto significa que después de un tiempo t la particula "olvida" su condicion inicial.
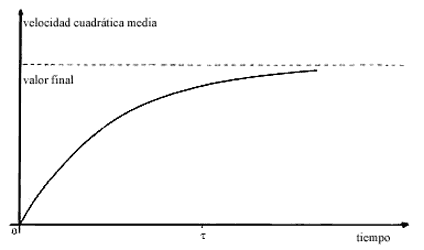
Figura 16. El valor cuadrático medio de las velocidades de la partícula browniana como función del tiempo.
En la figura 17 se muestran las distribuciones que va adquiriendo la velocidad al transcurrir el tiempo. Inicialmente (Figura 17, (a)) la distribución no tiene t ancho y está situada en el valor u0, que es valor inicial. En este instante se tiene la certeza de que la partícula tiene la velocidad u0. Al transcurrir el tiempo, la partícula empieza a sentir la presencia del fluido y, en consecuencia, el promedio de la distribución se separa de su valor inicial, y el ancho de la distribución aumenta (Figura 17, (b)). Después de un tiempo t la distribución adquiere una forma que ya no depende de las condiciones iniciales que tenía la partícula, es decir, se "olvidó" de ellas. Una vez que se adquiere esta distribución (Figura 17, (c)), ya no cambia al seguir transcurriendo el tiempo. Por tanto, el sistema partícula-fluido llega, en lo que a la velocidad respecta, a una situación de equilibrio. El tiempo t es, entonces, el tiempo que tarda la partícula en llegar a un estado de equilibrio con el fluido.
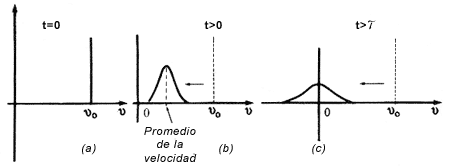
Figura 17. Evolución de la distribución de velocidades de una partícula browniana que inicialmente tenía una velocidad v0.
Nos damos cuenta de que hemos descrito un proceso irreversible en el que la velocidad de la partícula pasa de una distribución inicial a la de equilibrio con el fluido. Ahora bien, resulta que la distribución de velocidades en equilibrio mostrada en la figura 17(c) es justamente la misma que obtuvo Maxwell para la distribución de velocidades en un gas en equilibrio (véase el capítulo 11). Es decir, la distribución de velocidades que adquiere la partícula browniana al llegar a equilibrio con el fluido es marxwelliana.
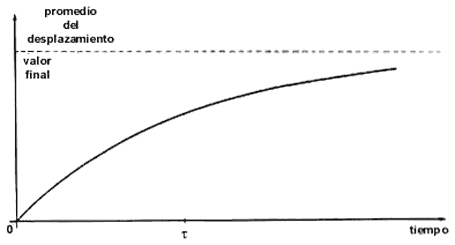
Figura 18. Promedio de desplazamiento de la partícula browniana al transcurrir el tiempo.
El promedio del desplazamiento en el transcurso del tiempo se muestra en la figura 18. El valor inicial es cero, ya que en un principio no ha habido ningún desplazamiento. Al transcurrir el tiempo, este promedio deja de ser nulo, y para tiempos del orden de t adquiere un valor constante.
El desplazamiento cuadrático medio d² (relacionado con la desviación estándar) que se obtiene, es el mostrado en la figura 6, justamente el predicho por Einstein. Para tiempos pequeños, la partícula se comporta como si fuera libre. En este régimen, aún no ha "sentido" al fluido. Al seguir transcurriendo el tiempo, el desplazamiento cuadrático medio queda descrito por la línea recta NM de la figura 6.
Ahora bien, resulta que en hidrodinámica se demuestra que este régimen corresponde al llamado régimen difusivo, que consiste en lo siguiente: si al inicio de la escala de tiempos se tienen en un lugar del recipiente muchas partículas (Figura 7), éstas comenzarán a difundirse por todo el fluido) como sucede si se deja caer una gota de tinta negra en un vaso de agua. Después de un tiempo q las partículas estarán repartidas homogéneamente en todo el líquido. Es decir, se habrá logrado una mezcla uniforme. Este tiempo q depende de la longitud del recipiente que ocupa el fluido.
En general, para casos físicos reales, el tiempo hidrodinámico q, es mucho mayor que el tiempo t de relajación asociado a la velocidad, que antes introdujimos. Así, un valor típico de q es de varios segundos (o más) mientras que t es del orden de milésimas de microsegundo.
Por lo tanto, vemos claramente que en este caso la partícula browniana pasa de un régimen de partícula libre (que es reversible) a otro régimen, el difusivo, que es irreversible.
En resumen, de los resultados anteriores podemos llegar a la conclusión de que se pueden distinguir varias escalas de tiempo en el comportamiento de la partícula browniana.
1) Tiempos pequeños, mucho menores que t. En este régimen la partícula se comporta como partícula libre. Todavía no "siente" que está inmersa en el fluido.
2) Tiempos grandes, mucho mayores que t pero menores que q. La interacción con el fluido hace que el comportamiento de la partícula se modifique completamente. En este régimen ocurren dos cosas: en primer lugar, las velocidades que va adquiriendo la partícula se modifican de forma tal que llega a un estado de equilibrio con el fluido; en segundo, la partícula empieza a desplazarse siguiendo un comportamiento difusivo. Es en este régimen de tiempos en que la velocidad y el desplazamiento de la partícula cambian su comportamiento a irreversible.
3) Tiempos hidrodinámicos. La partícula entra en un comportamiento determinado por la hidrodinámica. Después de un tiempo q la distribución de las partículas en el espacio será uniforme, obteniéndose así el equilibrio total, tanto en las velocidades, que ya se había alcanzado en el régimen anterior, como en las posiciones.
La descripción detallada que se acaba de dar indica la forma en que idealmente se debería tratar el comportamiento irreversible de cualquier sistema macroscópico. En particular, de manera natural deberían obtenerse de la descripción los diversos regímenes por los que pasa el sistema en su evolución al equilibrio. Naturalmente, también la evolución al equilibrio debe concluirse automáticamente de la descripción que se haga. Desafortunadamente, este programa no se ha podido realizar en general para otros sistemas más complicados. Sin embargo, basándose en lo aprendido en el caso del movimiento browniano, el físico soviético N. N. Bogoliubov hizo en 1946 suposiciones sobre la existencia de diversos regímenes en la descripción de fluidos. En particular, la suposición de la existencia de las diversas escalas de tiempo tiene papel muy importante en la descripción del comportamiento irreversible de un gas moderadamente denso.
Por otro lado, el tratamiento matemático requerido para especificar los comportamientos reseñados implica la utilización de cantidades estocásticas en las ecuaciones. Fue Norbert Wiener el primero que desarrolló esta cuestión, que corresponde a lo que en matemáticas se llama la teoría de funciones no-diferenciables.