II. ASPECTOS FUNDAMENTALES DE LA ÓSMOSIS

DESDE el punto de vista más fundamental de la razón de los porqués, la ósmosis no tiene una explicación. Generalmente sabemos qué papel desempeña la ósmosis en los organismos vivos, podemos predecir el movimiento osmótico en una circunstancia particular, pero no podemos explicar por qué ocurre el proceso de la ósmosis. Su presencia en los fenómenos biológicos relaciona una "función" y un "órgano" a nivel celular. La función es la ósmosis misma, el órgano es una membrana que la hace posible. La creación de la vida en nuestro planeta seguramente derivó de la evolución de los sistemas unicelulares en el desarrollo de una membrana que les permitiera un eficaz intercambio de materia con los alrededores. Aquí hay una razón de la presencia de la ósmosis en los sistemas biológicos al considerarse la evolución como selección natural.

De esta manera, el fenómeno de la ósmosis da sustento a la vida, la prolonga y la motiva, sabemos cómo ocurre, pero es insalvable su comprensión conceptual. En este misterio que hace de la ósmosis un fenómeno mágico, se desea destacar la naturaleza del problema que ahora nos preocupa, y, desde luego, ubicarlo en los ámbitos científico e histórico. Ahora examinaremos el ámbito científico, en vista de que el histórico ha quedado ya expuesto en el capítulo anterior.

Los conocimientos científicos relacionados con el fenómeno de la ósmosis están comprendidos en la rama de la fisicoquímica, y en particular en el tema de las soluciones. La teoría que describe estos hechos es por excelencia la termodinámica de equilibrio y la lineal de procesos irreversibles.

En efecto, la temodinámica de equilibrio describe la presión osmótica y la define como la presión requerida para mantener un sistema en estado de equilibrio. Los detalles de esta definición serán expuestos en el capítulo III. Por lo pronto nos interesa distinguir la condición básica y primordial que el formalismo clásico del fenómeno osmótico lleva en sí mismo.

La presión osmótica, como condición de equilibrio, será un concepto frecuentemente utilizado a lo largo de este libro, y es importante hacer notar que el concepto de presión osmótica ha cobrado realidad en el laboratorio y no en la naturaleza, porque los sistemas biológicos no son de equilibrio y generalmente realizan acciones transitorias en las que se realizan los procesos eficientemente. La descripción formal de la ósmosis se referirá más bien a un modelo muy simplificado en el laboratorio y no a una situación general de la naturaleza. Es decir, los sistemas biológicos son mucho más complicados que como se estudian en los cursos ordinarios de biofísica y de bioquímica, lo cual no debe desalentarnos ya que es a través de modelos como el hombre de ciencia describe a la naturaleza.

Mientras que el concepto de presión osmótica se establece en el contexto de la termodinámica clásica de equilibrio, el flujo osmótico es un concepto asimilado en la teoría termodinámica de no-equilibrio. Esta última teoría supone relaciones lineales entre flujos y fuerzas, siempre y cuando los flujos producidos no alejen severamente al sistema de su situación de equilibrio. La termodinámica de no-equilibrio es actualmente bien conocida, con sus postulados lógicos, autoconsistentes y suficientes para describir completamente la evolución del sistema a partir de cualquier situación hasta el estado de equilibrio.

Las dos teorías termodinámicas que hemos indicado no son suficientes para establecer la comprensión del mecanismo a través del cual la ósmosis ocurre, puesto que, aunque describen relaciones macroscópicas entre las variables de estado y sus efectos espaciales y temporales, no nos dicen como es la mecánica particular que se extralimita cuando se tiene un movimiento osmótico de masa.

Desde el punto de vista de la teoría cinética de los gases y de la mecánica estadística, el problema tampoco queda aclarado del todo, aunque de momento puede arrojar alguna luz sobre el particular. Es decir, dar una imagen microscópica a través de la cual se explique que el mecanismo de la ósmosis es un problema escasamente resuelto.

En el caso de la capilaridad, la causa intrínseca por la que una columna de agua en un capilar de vidrio se eleva sobre la superficie libre de un recipiente con agua, puede obtenerse microscópicamente. La capilaridad se define en términos de acciones moleculares al indicarse la existencia de una fuerza resultante entre la superficie del agua y la pared del capilar. Esta fuerza ejerce una acción que es opuesta a la dirección de la fuerza de gravedad y la causa que produce esa fuerza en la interfase agua-aire-capilar es la competencia entre las fuerzas de cohesión y de adherencia entre las moléculas de agua, del aire y del vidrio.

Ahora bien, una interpretación parecida en términos de dinámica molecular no ha sido establecida con respecto a la ósmosis, aunque algo se ha podido decir a este respecto utilizando para ello la mecánica estadística o la teoría cinética de los gases. Con la intención de observar las dificultades de la comprensión teórica de la ósmosis vamos a discutir, a continuación, los detalles particulares del fenómeno y su comprobación macroscópica.

Si no se conoce el fenómeno de la ósmosis y por casualidad se observa este fenómeno en un equipo experimental, lo primero que se advertirá es que su presencia contradice el sentido común porque el flujo osmótico ocurre precisamente en dirección contraria a la que se espera.

Cuando tenemos un sistema de vasos comunicantes separados entre sí por una barrera porosa, seremos capaces de hacer una predicción de la dirección del flujo del líquido entre los vasos. Así percibimos que, en efecto, el flujo se dirige del recipiente donde la altura del líquido es mayor, al recipiente donde la altura es menor (véase la figura 2).

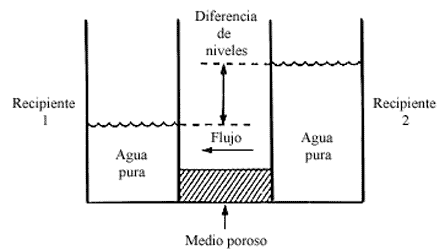
Figura 2. Un flujo volumétrico y viscoso se observa entre dos vasos comunicantes de un líquido a diferentes alturas que puede pasar un medio poroso.

La función de los vasos comunicantes es nivelar las diferencias de nivel del líquido entre los dos sistemas en contacto. De igual forma ocurre con la presencia de un flujo calorífico, originado por una diferencia de temperaturas entre dos puntos. En este caso, el flujo de calor ocurre del punto donde la temperatura es mayor a donde la temperatura es menor.

Sin embargo, en el sistema mencionado de vasos comunicantes haremos un cambio, en lugar de poner agua pura en el recipiente 2, colocaremos una solución de agua con azúcar, y en vez de ponerlo en contacto con el recipiente 1 empleando un medio poroso, utilizaremos una membrana semipermeable que permita el libre tránsito del agua, pero que impida la difusión del azúcar. Entonces ocurre algo sorprendente, la dirección del flujo que teníamos antes (véase la figura 2) se invierte. Ahora el flujo del agua es contrario a la dirección natural que tendría si los recipientes fueran vasos comunicantes (véase la figura 3).

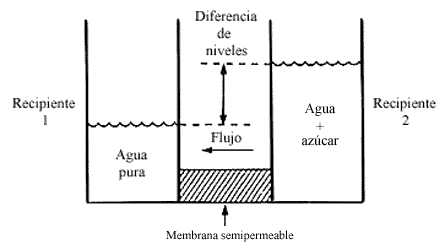
Figura 3. Un flujo volumétrico y viscoso se observa entre dos recipientes con soluciones de diferente concentración. El flujo de la solución diluida hacia la solución concentrada es el flujo osmótico.

Un novato que contemple este fenómeno directamente frente al experimento, seguramente se sorprendería mayúsculamente, porque la columna del líquido de uno de los recipientes se eleva a costa de reducir la altura del vaso contiguo. El fenómeno observado alcanza el estado de equilibrio cuando entre los recipientes se observa una diferencia de niveles que no cambia con el tiempo. Esto es lo inesperado, que el equilibrio mantenga una diferencia de presiones, en lugar de anularla como en el caso observado antes, en los vasos comunicantes. Así, la explicación más natural que el novato puede dar a dicho flujo osmótico y a la diferencia final de niveles es suponer la presencia de un pistón que presiona la columna de agua pura. Tal explicación falla porque dicho pistón no existe. Así pues, el novato se quebrará la cabeza queriendo dar una explicación en términos de "fuerzas" y sus efectos, pero al final de cuentas la causa de tales "fuerzas" no aparecerá por ningún lado.

¿Cuál es el error de apreciación que comete el novato que no le permite contemplar una explicación correcta? La respuesta es que el novato cree que una solución líquida frente a una membrana semipermeable se comporta como un fluido puro. Por lo anterior, el novato no considera ninguna información adicional relacionada con la propiedad de las soluciones y mezclas. El novato tendrá que aprender la teoría termodinámica de mezclas para entender que toda solución posee una "energía química" (energía libre) la cual es menor en la mezcla que en las correspondientes sustancias puras. Así pues, la energía química es mayor en el agua pura que en la solución de agua con azúcar; y otra vez se establece el fenómeno cotidiano por el sentido en que el flujo de masa ocurre, es decir, del punto donde existe un potencial mayor a donde hay uno menor. El potencial de que hablamos se refiere a la famosa "energía química".¹ Esto explica el fenómeno osmótico desde el punto de vista termodinámico. Posiblemente tal aseveración no satisfaga al lector porque la descripción de la energía química no despierta nuestro sentido de apreciación y la curiosidad misma queda en el vacío. Hemos de reflexionar en que la explicación que hemos dado es formal en relación a la teoría termodinámica y que, si no la entendemos en esa forma, estamos perdidos. Sea porque se le llame energía química, energía libre, o bien se nos dé una descripción en términos del concepto de entropía, no nos aclararía el mecanismo del fenómeno osmótico; y la pregunta que inquietó vivamente al novato sobre la causa mecánica de dicho fenómeno queda sin respuesta. Así se confirma el hecho ya comentado de que poco ayuda la teoría termodinámica para establecer el entendimiento de la ósmosis; por lo que recurriremos a la teoría cinética de los gases y la mecánica estadística en auxilio de la termodinámica. Algo se ha podido hacer para dilucidar el fenómeno a partir de las propiedades moleculares, aunque en general se trata de un deseo no satisfecho, porque esta explicación no está elaborada en forma completa y definitiva por los físicos. Por lo pronto podemos hacer referencia a las dificultades que involucra un estudio de este tipo y dar una idea de lo que la teoría cinética de los gases ideales establece para la ósmosis, como lo haremos a continuación.

Imaginemos un vaso con agua donde se coloca un conjunto de municiones de cobre. Lo que ocurre es que las municiones se depositan en el fondo del vaso y desde luego no producen ningún efecto osmótico. Si dividimos las municiones en fragmentos y los colocamos nuevamente en el agua, otra vez observamos que los fragmentos se depositan lentamente en el fondo del vaso. Ahora tampoco observamos un efecto osmótico. Este se conseguirá cuando se logre dividir los pequeños fragmentos metálicos de tal manera que las partículas producidas no se depositen en el fondo, sino que se distribuyan en el volumen del agua formando una suspensión. Ahora bien, las partículas que forman una suspensión son tan grandes, comparadas con los tamaños de las moléculas del agua, que un simple filtro (un medio poroso) funciona como una membrana semipermeable, ya que impide el libre paso de estas partículas. En este caso estaríamos en posición de observar el efecto osmótico de una suspensión. Sin embargo, si tuviéramos mil millones de partículas de cobre en la suspensión, apenas estaríamos considerando una presión osmótica de unas mil millonésimas de la presión atmosférica. De manera que, para que el efecto tuviera importancia y se observara en un experimento, se tendrían que dividir aún más las partículas de cobre. De esta forma llegaríamos al nivel de las dimensiones atómicas. Esto es si insistimos en apreciar con nuestros sentidos el efecto osmótico. En este caso ya no estaríamos hablando de una suspensión sino de una solución. En este ejemplo se destaca que 10⁹ partículas no permiten apreciar un resultado de efecto microscópico, sino que para ello requeriremos un número de partículas en disolución del orden de 10²³ (número de Avogadro). Con esto se destaca el hecho de que el fenómeno osmótico es francamente macroscópico y también se ilustra que, partiendo del punto de vista macroscópico, una descripción del hecho osmótico podrá hacerse considerando la superposición de la dinámica de un número muy grande de moléculas, en donde se pueden establecer resultados promedios, y esto es en realidad un tratamiento mecánico-estadístico a partir de la dinámica molecular que, como hemos dicho, es un procedimiento que no se ha elaborado en forma completa para explicar el fenómeno osmótico. La dificultad principal de este tratamiento es considerar a la membrana como una pared-frontera y describir su interacción con las partículas. Hasta ahora, los resultados obtenidos son promedios que implican operaciones matemáticas de un enorme grado de dificultad. De manera que la dinámica molecular que origina el flujo osmótico queda oculta, y volvemos a lo mismo: tenemos que considerar dicho fenómeno desde el punto de vista macroscópico.

Las informaciones que se han podido obtener sobre el mecanismo de la ósmosis se han realizado por medio de la teoría cinética de los gases. Ahora ilustraremos el tipo de información a que da lugar:

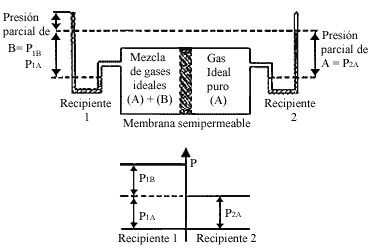
Figura 4. El gas ideal A puede pasar a través de la membrana que separa los recipientes 1 y 2. En equilibrio P 2A = P 1A. La presión total en el recipiente 1 excede a esta presión por P 1B, la presión osmótica.

Consideremos un dispositivo como el indicado en la figura 4, donde tenemos dos recipientes separados por una membrana semipermeable. En el recipiente 1 tenemos una mezcla de dos gases ideales que nombramos A y B, y en el recipiente 2 tenemos el gas ideal A puro, permeable a la membrana; mientras que la membrana es impermeable al componente B.

Bajo condiciones de equilibrio ocurre que la presión parcial del componente que puede pasar a través de la membrana es igual en ambos compartimientos, es decir

P_2A=P_1A

En este caso, en el recipiente 1 tenemos un exceso de presión causado por el componente B. Este exceso de presión no es observado en el gas del recipiente 2, porque de alguna manera es compensado por la membrana al impedir el libre tránsito del componente B. En efecto, en un balance de presiones es la membrana la que contrarresta los efectos del componente que no puede pasar y así se estima la función de la membrana. De manera que si observamos los manómetros del dispositivo experimental, el sistema conserva su equilibrio, acusando una diferencia de presiones. En este caso, nótese cómo la presión osmótica es la presión parcial del componente que no puede pasar a través de la membrana

p=P_1B

A este efecto, algunos autores suelen llamarlo "efecto de manómetro", porque son éstos los que señalan la diferencia de presiones cuando el sistema está en equilibrio. Este hecho tiene una consecuencia importante cuando el sistema está fuera del equilibrio, puesto que la diferencia de presión del componente que puede pasar no será igual a la diferencia de presión registrada por los manómetros.

Si consideramos

D p Diferencia de presión a ambos lados de la membrana (medida),

entonces

Dp-p Es la caída de presión del componente que puede pasar a través de la membrana.

La corrección a la presión medida (Dp) por la presión osmótica (p) es para evitar el exceso de presión del componente que no puede pasar y que los manómetros registran, aunque sin importancia en el flujo a través de la membrana. El efecto de manómetro nos hace considerar la naturaleza del flujo osmótico, ya que en la explicación que hemos dado con gases ideales se indica que la presión osmótica aparece como una corrección entre una predicción teórica y su ajuste experimental. Asimismo, observaremos a continuación que el dispositivo empleado con gases ideales no indica a simple vista la causa del flujo osmótico.

Si consideramos que el dispositivo experimental de la figura 4 no se encuentra en equilibrio, es decir

P_2A ¹ P_1A

entonces se obtendrá un flujo de la especie A (que puede transitar libremente a través de la membrana), producido por la diferencia entre las presiones P_2A y P_1A. Ahora demostraremos que este flujo no es osmótico. La demostración es muy simple, porque en un gas ideal la presión parcial es proporcional a la concentración, de manera que el flujo es causado por una diferencia de concentraciones de la especie A a través de la membrana, y bien se sabe que es un flujo de difusión que se ajusta a la Ley de Fick de la difusión. Por lo que respecta al flujo osmótico es no difusivo y equivalente al causado por una diferencia de presiones. En nuestro caso, en un estado de no equilibrio, además del flujo difusivo del componente A, observaríamos un flujo del mismo componente A causado por p =p_1B. Para observar de dónde surge este término en nuestras ecuaciones, es necesario utilizar el formalismo completo de la teoría cinética de Boltzmann, para encontrar que, en efecto, es la presión osmótica de los componentes por lo que no pueden pasar por la membrana, y son los que producen el flujo osmótico. Pero este término aparece junto al que origina el flujo viscoso. Es decir, el flujo osmótico puede interpretarse como un flujo viscoso, producido por los movimientos térmicos moleculares cuando son interrumpidos por una pared porosa (membrana).

La descripción matemática de este hecho fue realizada por L. F. del Castillo, E. A. Mason y H. E. Revercomb en 1979, dándole una expresión formal a la sugerencia que consideraba al flujo osmótico de origen viscoso, descripción cualitativa dada por varios autores cuando estudiaron la naturaleza hidrodinámica de la ósmosis. Reanudaremos esta explicación en el capítulo VI.

NOTAS

1 Cualquiera de nosotros puede interpretar la ósmosis como la originada por un efecto de succión, de una solución concentrada hacia una solución diluida. Tal efecto de succión no se produce mecánicamente como se absorbe el jugo de una naranja con la boca, sino que se trata de un efecto de succión producido por una diferencia de energías químicas.