III. ¿QUÉ NOS DICE LA TEORÍA CINÉTICA?

AL EXPRESAR la ley de Dulong-Petit, como resumen de un número importante de resultados experimentales, no se ha hecho ninguna consideración específica sobre la estructura microscópica de las sustancias que están bajo estudio. Es decir, tal como se han presentado las cosas, no ha tenido ninguna relevancia que las sustancias estén formadas por átomos o no. Se dice que estos resultados son macroscópicos. Sin embargo, por otro lado se sabe que efectivamente las sustancias están formadas por átomos, por lo que uno podría preguntarse lo siguiente: ¿qué efecto en las propiedades macroscópicas de las sustancias tiene este hecho? Con más precisión, si uno supone que las partículas microscópicas se mueven siguiendo las leyes de la mecánica de Newton, entonces ¿es el comportamiento microscópico compatible con las leyes macroscópicas que rigen el comportamiento de las sustancias? La parte de la física que ha estudiado esta pregunta es la teoría cinética.

Hagamos un breve paréntesis para presentar el contexto histórico a mediados del siglo pasado.

Desde la antigñedad griega muchos pensadores elucubraron acerca de la composición de la materia. Diversas hipótesis se propusieron, sin que, en general, tuvieran verdaderas bases científicas. Además, estas hipótesis tampoco tuvieron aceptación general. Fue de hecho hasta principios del siglo XIX que con los trabajos de John Dalton (1766-1844) se empezaron a dar los primeros pasos serios en el estudio de la estructura atómica de la materia. Posteriormente también contribuyeron de manera muy importantes personas como Gay-Lussac, Amedeo Avogadro (1766-1856) y Jñns Jacob Berzelius (1779-1848). Así, hacia mediados del siglo pasado ya se tenía un adecuado, aunque no completo, cuerpo de teoría que implicaba que la materia estaba compuesta de partículas microscópicas, llamadas átomos. Es de mencionar que en esa época esta hipótesis no fue aceptada, de ninguna manera, por la mayoría de los científicos. Fueron relativamente pocos los que la aceptaron.

Hacia mediados del siglo XIX se presentaba la siguiente situación. Por un lado se habían planteado las leyes de la termodinámica, que se refieren a aspectos macroscópicos del comportamiento de las sustancias, y por el otro se vislumbraba cada vez con mayor claridad que la materia estaba compuesta de átomos. Surge entonces la pregunta de cómo conciliar estas dos posiciones. Dicho en otras palabras, la cuestión es: si la materia, en efecto, está compuesta de partículas microscópicas, entonces ¿qué consecuencias macroscópicas tiene el comportamiento microscópico de una sustancia?

Este problema ya se había planteado desde el siglo XVII, entre otros por Robert Boyle (1627-1691). En el siglo XVIIl continuaron trabajando en él Leonhard Euler (1707-1783) y Daniel Bernoulli (1700-1782). Estos estudiosos obtuvieron algunas consecuencias a las que, sin embargo, no se les prestó la debida atención a causa de que, por un lado, no se aceptaba la hipótesis atómica y por el otro, porque muchos de los conceptos utilizados eran bastante oscuros.

Fue la primera mitad del siglo XIX cuando se empezaron a dar los primeros pasos en firme. Varios trabajos de J. Herapath presentados alrededor de 1820 y de J. J. Waterston alrededor de 1845 volvían a tomar la cuestión. Sin embargo, fue hasta casi mediados de siglo que este tipo de teorías tuvo un feliz renacimiento. En efecto, entre 1850 y 1875 August Krönig (1822-1879), Rudolph Clausius (1822-1888), James C. Maxwell y Ludwig Boltzmann (1844-1906) desarrollaron las bases de la moderna teoría cinética de la materia. Supusieron que las sustancias estaban compuestas de átomos y a partir de su comportamiento microscópico pudieron obtener como consecuencia algunas propiedades macroscópicas. En particular pudieron explicar diversos fenómenos, así como fundamentar varios resultados que ya se conocían en la termodinámica. Se pudieron calcular, por ejemplo, propiedades tales como el calor específico, la conductividad térmica, la viscosidad de gases poco densos en términos de las propiedades de los átomos que los constituyen.

Asimismo, hemos de mencionar que, entre otras cosas, Maxwell obtuvo, también como resultado de estos trabajos, la distribución de las velocidades de los átomos en un gas en equilibrio. Esta cantidad indica cuántos átomos de un gas tienen cierto valor de la velocidad. Así, se puede saber cuál es la velocidad que tiene la mayoría de los átomos. Maxwell encontró cómo depende esta distribución de la temperatura del gas, de la masa del átomo, etc. A esta distribución se le llama maxwelliana. En la figura 2 se muestra una gráfica de esta distribución a una temperatura fija. Con este resultado, Maxwell pudo obtener las magnitudes de las velocidades que tienen las partículas en un gas. Por ejemplo, encontró que a temperatura ambiente (t = 30ñC) la velocidad Vm (figura 2) que tienen la mayoría de lo átomos en un gas de nitrógeno es aproximadamente igual a 600 m/s, o sea, 2 160 km/h.

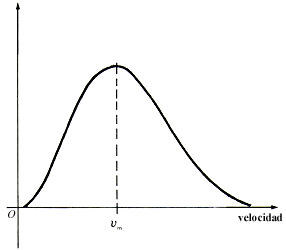
Figura 2. Forma de la distribución de las velocidades de las partículas de un gas en equilibrio. Las partículas no tienen la misma velocidad. Esta distribución se llama maxwelliana, en honor de su descubridor.

El mismo Maxwell realizó varios experimentos en los que verificó algunas de las predicciones teóricas hechas para la conductividad y la viscosidad de un gas poco denso. Años después se verificó experimentalmente que un gas en equilibrio efectivamente tiene la distribución de velocidades predicha por Maxwell.

Si se conoce cómo están distribuidas las velocidades de las partículas de un gas, uno puede encontrar entonces el promedio de la energía cinética de cada una de las partículas. Esto lo hizo por primera vez Maxwell en 1859, encontrando lo siguiente. Si el gas está en equilibrio a una temperatura absoluta T, 1 entonces cada partícula que compone el gas tiene una energía igual a (3kT/2). Aquí k es una cantidad constante, llamada la constante de Boltzmann 2 . Este resultado significa que, en promedio la energía del gas se distribuye de manera uniforme entre las partículas que lo componen. A esto se le llama el principio de equipartición de la energía.

Posteriormente, en 1868, Boltzmann generalizó este teorema al caso en que las partículas del gas no fueran rígidas —que es una suposición que había hecho Maxwell—, sino que también tuvieran movimientos internos.

Veamos este principio con un poco más de detalle. De hecho, de la forma expresada arriba, solamente es válido para gases compuestos de partículas que solamente tienen un átomo, por ejemplo, neón o argón. En este caso cada uno de ellos solamente tiene posibilidad de movimiento traslacional, y dado que se puede mover en tres dimensiones se dice que tiene tres grados de libertad. El principio de equipartición de la energía dice, con más precisión, que la energía se reparte de manera tal que cada grado de libertad tiene asociada una energía igual a (kT/2). Como un átomo tiene tres grados de libertad, en total tiene asociada una energía igual a 3 x (kT/2) = (3kT/2), que es el valor predicho por Maxwell.

Una vez conocida la energía de un gas monoatómico (de un solo átomo) se puede encontrar su calor específico. Se encuentra como consecuencia del principio de equipartición de la energía que cada grado de libertad contribuye con (k/2), o sea que el calor específico por cada átomo es entonces igual a (3k/2). Nótese que esta cantidad no depende de la temperatura, es decir, es una cantidad constante. Además, este valor corresponde justamente al que se encuentra de las mediciones experimentales. Como se recordará, éste es precisamente el enunciado de la ley de Dulong-Petit.

De esta manera se pudo fundamentar, a partir de las propiedades microscópicas de las sustancias, la ley macroscópica de Dulong-Petit, por lo menos para gases monoatómicos.

Una vez encontrado el principio de equipartición de la energía se aplicó a otros gases distintos a los monoatómicos. El siguiente paso es considerar gases formados de moléculas constituidas por dos átomos, es decir, gases diatómicos. En este caso, el número de grados de libertad de cada una de estas partículas es 6, ya que tres de ellos corresponden al centro de masa de la molécula (que corresponde al movimiento traslacional de la molécula como un todo); dos más corresponden a los ángulos necesarios para dar la orientación en el espacio de la línea que une a los átomos, por ejemplo q y j de la figura 3; uno más corresponde a la distancia entre los átomos. Aplicando el principio de equipartición de la energía se obtiene que el calor específico de este tipo de gas sería 6*(k/2)=3k. Si ahora se compara este valor con el medido experimentalmente, resulta que ya no hay concordancias. El valor medido es menor que esta predicción.

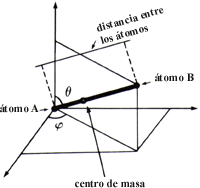
Figura 3. La dirección de la línea que une a los dos átomos de una molécula diatómica queda completamente especificada si se dan los ángulos q y j mostrados.

De manera análoga, al aplicar el principio de equipartición de la energía al caso de gases compuestos de moléculas con más de dos átomos, es decir, poliatómicas, resulta que se encuentra para el calor específico un valor constante que no concuerda con lo que se mide experimentalmente.

Otro sistema al que se aplicó el principio de equipartición de la energía fue a los sólidos. Aquí las partículas que componen el sólido se encuentran localizadas en un arreglo geométrico regular que se llama la red cristalina. En la figura 4 se muestra esquemáticamente una red cristalina en dos dimensiones. Las partículas pueden oscilar alrededor de estos puntos. En este caso se encuentra, aplicando el principio de equipartición de la energía, que el calor específico por cada partícula es igual a 3k, que concordaba muy bien con los valores medidos en muchos sólidos.

Figura 4. Esquema de una red o malla cristalina en dos dimensiones.

Por tanto, la teoría cinética predecía valores de calores específicos que, por lo menos en algunos sistemas físicos, concuerdan muy bien con los valores medidos experimentalmente. Solamente los casos de los gases diatómicos y poliatómicos no pudieron ser explicados por la teoría cinética entonces existente. Hay que notar que son justamente estas sustancias sobre las que había ya discrepancias entre el enunciado de la ley de Dulong-Petit y los valores medidos (ver final del capítulo II).

NOTAS 1 La temperatura T en la escala absoluta (medida en grados Kelvin, ñK) está relacionada con la temperatura t (medida en grados centígrados, ñC) de la escala de Celsius, que nos es familiar, por medio de la fórmula T= 273 + t. 2 El valor de k es 1.38 x 10^-23 joule / ñK