V. TEORÍA CUÁNTICA DE LOS ÁTOMOS COMPLEJOS

ESA nueva física, basada en nociones probabilísticas y en el principio de incertidumbre, es heredera de los viejos cuantos de Planck. Por ello se le conoce como mecánica cuántica. Con la teoría cuántica se han podido explicar las propiedades de los átomos y moléculas, las reacciones entre ellos y sus consecuencias químicas. En particular, podemos entender las regularidades que Mendeleyev plasmó en su tabla periódica de los elementos químicos.

Los químicos del siglo pasado sabían bien que el hidrógeno era el elemento más ligero y que su átomo sería el más simple: en el modelo planetario un electrón con carga e daría vueltas atraído eléctricamente por el primero de los núcleos, el protón. La ecuación de la mecánica cuántica, llamada ecuación de Schrñdinger, puede resolverse en este caso y a su solución se le llama la función de onda y, relacionada con la probabilidad de encontrar al electrón en distintos puntos del espacio que rodea al protón.

La función y tiene tres características: tamaño de la región en el espacio donde y no es nula, su forma geométrica y su orientación. La primera característica de la función y equivale al tamaño del átomo, es decir, de la región donde está confinado el electrón. Esto fija la longitud de onda l típica que debe asociarse al electrón dentro del átomo. De acuerdo al principio de incertidumbre, el momento lineal correspondiente debería ser del orden de / l. Como la energía cinética es p²/2m_e, donde m_e es la masa del electrón, l determina la energía del átomo de hidrógeno. En otras palabras, el tamaño de un sistema cuántico está relacionado con su energía. Mientras menor sea la región de confinamiento, más energía se requiere para mantenerlo estable.

Podemos tener una idea del tamaño del átomo de hidrógeno, cuyo radio es R, si igualamos la energía eléctrica que lo confina, e²/R, a la energía cinética que el confinamiento induce,

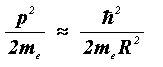
De aquí resulta que R = ²/m_ee² que, por cierto, es la única combinación de , m_e y e que tiene las dimensiones de longitud. El radio se conoce como el de Bohr y vale 0.5 x 10^-8 centímetros. Si el átomo fuera del tamaño de una pelota de futbol por ejemplo, un hombre tendría una altura bastante mayor que la distancia entre la Tierra y la Luna. ñAsí de pequeños son los átomos! No ha de extrañarnos, pues, que las leyes físicas que rijan en el mundo de los minúsculos átomos sean distintas a las que vemos en acción en nuestra vida diaria.

Una vez que conocemos R, podemos estimar las energías típicas de un electrón dentro del átomo. Obtenemos que esa energía E es del orden de m_ee⁴/2², equivalente a 20 x 10^-12 ergs, donde el erg es la unidad de energía en el sistema CGS.¹ Como vestigio de las órbitas cuantizadas de Bohr, la energía del electrón sólo puede tomar ciertos valores discretos. Con ello, la teoría cuántica explica el espectro del átomo de hidrógeno, que había sido observado por Balmer, Lyman y otros ópticos del siglo diecinueve.

La segunda característica de y es su forma geométrica. De la misma manera en que hay tamaños discretos de y, así sólo algunas formas de y satisfacen la ecuación de Schrñdinger. Con y entra en la física la forma geométrica. Resulta curioso, pero no había en la teoría clásica de la física algo relacionado con la forma de las cosas. Y eso a pesar de que la naturaleza está llena de formas, desde las facetas de un cristal a los pétalos de las flores.

Según sea la forma de y, sus propiedades ante las rotaciones cambian. Dinámicamente, en la antigñedad se sabía que el momento angular 1 caracteriza las propiedades de rotación de un sistema físico. Distintas formas de y, pues, corresponden a diferentes valores del momento angular. Y sólo ciertas formas son permitidas porque solamente ciertos valores del momento angular 1 son posibles. Esta variable dinámica, al igual que la energía, toma valores discretos: está cuantizada, como dicen los físicos.

La teoría de Schrñdinger para el átomo de hidrógeno resultó satisfactoria hasta que se enfrentó a un nuevo hecho experimental. Los físicos alemanes Stern y Gerlach hicieron pasar un haz, formado por átomos de hidrógeno, entre los polos de un imán asimétrico, de diseño especial; observaron que el haz se parte en dos. Ello significa que el átomo de hidrógeno, neutro eléctricamente, tiene propiedades magnéticas que la teoría anterior no contiene ni logra explicar. Hubo que enmendar la teoría de Schrñdinger y asociarle un momento magnético al electrón, como si fuera un cuerpo cargado en rotación. A esta rotación intrínseca se le llamó espín (de la palabra inglesa spin, que significa giro). El espín, como toda variable dinámica en la teoría cuántica, también está cuantizado. Los resultados del experimento de Stern y Gerlach indican dos posibles orientaciones del espín del electrón, por lo que decimos que esta partícula tiene espín igual a 1/2: sus dos orientaciones son hacia arriba, proyección +1/2, o hacia abajo, proyección del espín igual a -1/2. Como luego veremos, el espín es una propiedad ubicua e importantísima en el mundo microscópico. Todas las partículas muy pequeñas tienen espín.

Átomos más complejos que el hidrógeno constan de muchos electrones, digamos Z, que orbitan alrededor de un núcleo con carga positiva. Ya que el átomo es neutro eléctricamente, el núcleo más pesado debe tener más carga, siempre un múltiplo entero de la carga e del protón. A Z se le llama el número atómico. Mientras más grande sea Z, menor resulta la repulsión entre los electrones comparada con la fuerza de atracción que sobre cada uno ejerce el núcleo. Ello conduce a órbitas electrónicas de menor tamaño. En conclusión, mientras más pesado el átomo, menor debería ser su tamaño.

Experimentalmente sabemos que la última afirmación es falsa. Algo mal debe haber en el razonamiento anterior. Lo que ocurre es que no todos los Z electrones caben en la misma órbita. Los electrones pertenecen, dentro del zoológico cuántico, a un tipo de partículas que son muy poco sociables, que repelen a sus semejantes. Si un electrón tiene una cierta energía, o una velocidad, o una posición dada, en fin, si está en un cierto estado cuántico, otro electrón no cabe ahí. Con este principio, que Pauli postuló y llamó el principio de exclusión, podemos entender el tamaño y la estructura no sólo de átomos complejos, sino también de los núcleos y de muchos otros sistemas cuánticos. El principio de Pauli es una de las piedras angulares de la física cuántica y sus aplicaciones; nunca se ha encontrado una violación a sus mandatos.

NOTAS

1 Cuando se usan tantas potencias de 10 los cálculos se vuelven engorrosos y la memoria falla. Esas potencias negativas de 10 aparecen al hablar de átomos porque el sistema de unidades empleado es conveniente cuando se trata con sistemas físicos a la escala del hombre. Si se describen sistemas muy grandes, como las galaxias, o muy pequeños, como los átomos, es conveniente usar sistemas de unidades a la medida. Así, ²/m_ee² es la longitud natural para los átomos y m_ee⁴/2² es la unidad natural de energía. Por ello se introdujeron el ñngstrom (ñ), igual a 10^-8 cm, y el electrón-voltio (eV), igual a 1.6 x 10^-12 erg y a la energía que una carga eléctrica igual a la del electrón adquiere cuando se le acelera con una diferencia de potencial de un volt. El radio de Bohr vale medio ñngstrom, aproximadamente, y la energía para arrancarle un electrón al átomo de hidrógeno equivale a 13.6 eV.