IV. LAS CATÁSTROFES ULTRAVIOLETA Y ATÓMICA

MIENTRAS los grandes experimentadores de finales del siglo XIX se hallaban ocupados en descubrir partículas y radiaciones, los teóricos de los albores del nuevo siglo no se quedaban quietos sentados tranquilamente en sus lares: la mecánica de Newton y el electromagnetismo de Maxwell. En efecto, el gran teórico alemán Max Planck habría de conmocionar al mundo científico cuando en 1900 resolvió un viejo problema, a costa de sacrificar ideas muy enraizadas. Para eliminar la así llamada catástrofe ultravioleta,¹ Planck debió suponer que la energía de las ondas electromagnéticas viene en paquetes, que él llamó cuantos. Sólo cinco años después, Einstein reforzó las ideas de Planck al sugerir que la luz está formada por fotones, partículas de luz cuya energía es proporcional a la frecuencia de la onda electromagnética. Esta última, según la teoría de Maxwell y sus múltiples comprobaciones posteriores, es la radiación que forma la luz.

Tanto en el trabajo de Planck sobre la radiación del cuerpo negro y la eliminación de la catástrofe ultravioleta, como en el trabajo de Einstein, que explica el efecto fotoeléctrico en que un rayo de luz arranca electrones de un metal, hace su aparición la hoy famosa constante h, llamada de Planck. La energía E del fotón, el cuanto de luz, y la frecuencia v de la onda electromagnética se ligan a través de la constante de Planck:

E = hv.

El valor de h necesario para ajustar los datos experimentales del cuerpo negro y del efecto fotoeléctrico es el mismo y resulta muy pequeño cuando usamos unidades propias para entender los fenómenos de nuestra vida cotidiana. En el sistema CGS (centímetro-gramo-segundo) la constante de Planck toma el pequeñísimo valor

h = 6.625 x 10^-27 (grs. cm²/s²).

La pequeñez de h, como veremos, nos explica muchas cosas. En particular, la razón por la cual la mecánica de Galileo y Newton basta para explicar el movimiento de los cuerpos grandes.

Empero, después de los descubrimientos de Rutherford y su propuesta del modelo planetario del átomo, restaba una catástrofe, la catástrofe atómica. En efecto, si el átomo es como un sistema solar minúsculo, mantenido por fuerzas eléctricas y sujeto a las leyes mecánicas de Newton y a las leyes electromagnéticas de Maxwell, tiene una vida por demás efímera. Una carga acelerada, según la teoría clásica, radia energía al emitir ondas electromagnéticas. Esa energía la toma de su movimiento, disminuyendo siempre su velocidad. Con ello se acerca cada vez más al centro que lo atrae. La teoría clásica —como llaman ahora los físicos a la ciencia vigente en el siglo XIX— predice que cada electrón caería al núcleo atómico en apenas una diezmillonésima de segundo. En consecuencia, los átomos y la materia por ellos formada serían inestables. Para empeorar aún más las cosas atómicas, el espectro atómico resulta también inexplicable con la teoría clásica. La frecuencia de la luz radiada por los electrones que simulan planetas es continua y no contiene rastros del espectro atómico, formado por líneas de luz con frecuencias discretas.

El primer físico que aventuró una hipótesis razonable para eliminar esta catástrofe atómica fue el gran científico danés Niels Bohr, cuyo centenario celebramos en 1985. Bohr viajó de su natal Dinamarca a Manchester en 1913, para trabajar en el laboratorio de Rutherford. Allí tuvo una idea brillante: entre las posibles órbitas que un electrón puede recorrer alrededor del núcleo hay algunas de carácter especial. Esas órbitas son estacionarias, pues un electrón permanece ahí si no se le perturba. El átomo sólo emite luz cuando el electrón va de una órbita estacionaria a otra. La frecuencia de esa luz está ligada, otra vez, con la constante de Planck: hv es la diferencia de energía entre las órbitas estacionarias. Todo ello parece un juego de niños, una simple casualidad matemática, pero Bohr logró de esta manera correlacionar los datos observados por los ópticos del siglo pasado y explicar el espectro del átomo más simple, el de hidrógeno. En todo caso, h vuelve a hacer su aparición en la física atómica.

Si bien las ideas de Bohr no fueron refutadas, en sí no constituían una teoría del mundo atómico. Esta comienza a tomar forma cuando el noble francés Louis de Broglie escribe su tesis doctoral en 1924 y propone que a toda partícula debe asociarse una onda, cuyas características dependen del estado dinámico de la partícula. Por ejemplo, si la partícula es libre, sólo su momento lineal p —igual al producto de su masa por su velocidad— basta para determinar su estado de movimiento; en tal caso, la longitud de onda asociada es igual a h/p. Se da origen así a la dualidad partícula-onda.

Poco después de que De Broglie presentó sus ideas sobre la mecánica ondulatoria, el físico austriaco Erwin Schrñdinger supuso que la relación de De Broglie es válida para toda partícula, incluso para un electrón dentro del átomo. Las órbitas estacionarias de Bohr serían aquellas para las cuales un número entero de longitudes de onda pudieran acomodarse en el perímetro de la órbita. Esto sólo era posible para ciertos valores de la longitud de onda, por consiguiente del momento lineal y, por tanto, de la energía. Volvían a aparecer los valores discretos de la energía y con éstos una explicación natural de los espectros atómicos.

Sin embargo, la dualidad partícula-onda debe repugnar a todo físico que se respete. Para definir una partícula, un punto material, se requiere un conjunto de operaciones en buena medida opuestas a las necesarias para precisar lo que es una onda. Partícula y onda son conceptos complementarios y de ninguna manera puede satisfacernos un concepto ad hoc como el de complementaridad, de acuerdo al cual un electrón a veces actúa como onda y a veces como partícula, según convenga al experimento que deseemos interpretar.

La solución a esta paradoja la dio un joven físico alemán, Werner Heisenberg, al postular el principio de incertidumbre. Ocurre que la posición y la velocidad de una partícula no pueden medirse al mismo tiempo. Si se quiere precisar dónde está la partícula, su momento lineal se vuelve indefinido, y viceversa: al tratar de definir la velocidad dentro de límites estrechos, se conoce menos dónde se halla la partícula. En forma más precisa, el principio que Heisenberg dio a la física moderna dice que el producto de la indeterminación del momento lineal por la incertidumbre en la posición es una cantidad del orden de h, la constante de Planck dividida por 2p:

= 2 / 2p

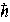
Cuando es despreciable, casi cero, momento lineal y posición pueden definirse con tanta acuciosidad como se desee; en tales casos, las órbitas clásicas existen y recuperamos lo bien sabido en la mecánica de Newton. Esto ocurre cuando tratamos con cuerpos grandes, como los planetas o una pelota de futbol. Ellos se mueven como si fuera cero y el principio de incertidumbre no actuara. Empero, cuando la masa de la partícula es muy pequeña, como la de un electrón que vale del orden de 9 x 10^-28 gramos, el principio de Heisenberg entra en acción y las nociones clásicas pierden validez; en particular, la trayectoria de un electrón no existe.

Si en una teoría se elimina un elemento, otro ha de reemplazarlo. Si ya no existen las trayectorias clásicas sino las ondas de De Broglie o de Schrñdinger, ¿cómo es que éstas reemplazan al viejo concepto de órbita? La respuesta a esta crucial pregunta, necesaria para formular un cuadro teórico coherente y completo, la dio Max Born, poco después de que Schrñdinger y Heisenberg postularan las ideas anteriores. Según Born, la onda que acompaña a la partícula da la probabilidad de encontrarla. Donde la onda es nula, es imposible hallar la partícula. Pero en aquellas zonas del espacio donde la amplitud de esa onda sea distinta de cero, sabemos que es probable encontrar a la partícula, aunque nunca tengamos la certeza completa. El principio de Heisenberg destruyó la certidumbre y el determinismo clásicos; por ello se le llama el principio de incertidumbre. Es, sin duda, uno de los pilares de la física actual.

NOTAS

1 Esta catástrofe ultravioleta surge al estudiar la radiación electromagnética de un cuerpo negro, que no es otra cosa que una cavidad con ondas electromagnéticas dentro y a la cual se ha hecho un agujerito por donde pueda escapar la radiación. Si para estudiar este problema, se unen la mecánica a la teoría electromagnética y a la mecánica estadística clásicas, resulta que, mientras mayor sea la frecuencia de las ondas mayor es la energía emitida por el cuerpo negro. Esto no concuerda con lo observado experimentalmente y repugna desde el punto de vista teórico. Por eso constituye una catástrofe. Como además, ocurre a frecuencias altas, como la de la luz ultravioleta, tal desastre de la física decimonónica recibió el sugerente apelativo de catástrofe ultravioleta.