II. SISTEMA MUSCULAR
UNA propiedad muy general de la materia viviente es la habilidad
para alterar su tamaño o medida por contracción o expansión de una zona determinada
del organismo. En el cuerpo humano existen grupos de células especializadas
en contraerse o relajarse sin que tenga que cambiar su posición ni su forma;
ciertos grupos celulares se contraen y se relajan bombeando líquidos, como es
el caso del corazón; otros fuerzan la comida a través del tracto digestivo;
etc.; los agregados de estas células especializadas se llaman tejidos musculares
o simplemente músculos. Un grupo de ellos tiene asignado como trabajo
el llevar a cabo la locomoción.
Los músculos son transductores (es decir, traductores) que convierten la energía química en energía eléctrica, energía térmica y/o energía mecánica útil. Aparecen en diferentes formas y tamaños, difieren en las fuerzas que pueden ejercer y en la velocidad de su acción; además, sus propiedades cambian con la edad de la persona, su medio ambiente y la actividad que desarrolla. Desde el punto de vista anatómico se pueden clasificar de muchas maneras, dependiendo de su función, innervación, localización en el cuerpo, etc. Quizá la clasificación histológica es la más sencilla y clara, y distingue dos clases de músculos: lisos y estriados. Los estriados, vistos al microscopio, parecen alternar bandas oscuras y claras distribuidas en forma regular; las fibras son largas. Los lisos consisten de fibras cortas que no presentan estrías.
El estudio de los músculos desde el punto de vista físico abarca muchos campos. Aquí trataremos el problema de la locomoción, que corresponde a los músculos estriados, los cuales tienen, en los extremos, sus fibras atadas por tendones que los unen a los huesos, por lo que se conocen como músculos del esqueleto.
Hablar de locomoción es hablar de movimiento, es decir, de mecánica. Lo primero que haremos será distinguir entre un cuerpo en movimiento y otro inmóvil. Un cuerpo inmóvil no cambia de lugar al tanscurrir el tiempo, mientras que uno en movimiento sí lo hace. Podemos pensar que un cuerpo inmóvil está en equilibrio, pero ¿qué es el equilibrio? Cuando hablamos de equilibrio en física, lo que estamos diciendo es que no hay fuerza neta actuando sobre el cuerpo, lo que implica que puede estar en movimiento y su velocidad ser constante; si la velocidad es cero, el cuerpo estará inmóvil.
La fuerza neta es cero cuando la suma de las fuerzas que actúan sobre el cuerpo
es cero, lo que se representa como: 
.
F representa a cada una de las fuerzas que actuán sobre el cuerpo y tiene carácter
vectorial, es decir, posee magnitud, dirección y sentido; en estas tres particularidades
deben sumarse las fuerzas.
Para saber si un cuerpo está o no en equilibrio, podemos hacer una representación gráfica de las fuerzas que actúan sobre él; por ejemplo, consideremos que las fuerzas que están actuando sobre el cuerpo están dadas por: F1, F2, F3 y F4 como se muestra en la figura 4, donde el tamaño de cada una es proporcional a su longitud, la dirección y el sentido están representados por la punta de la flecha. Para sumarlas gráficamente las dibujamos de manera consecutiva, de modo que se forma un polígono; si éste es cerrado, entonces la suma de las fuerzas es cero y el cuerpo está en equilibrio; si el polígono no es una figura cerrada, habrá una fuerza neta actuando sobre el cuerpo.
Hay un caso que debe ser considerado: si las fuerzas que actúan sobre el cuerpo
tienen la misma magnitud y dirección pero sentidos contrarios, la suma vectorial
es cero; sin embargo, el cuerpo estará en equilibrio sólo si están aplicadas
sobre la misma línea, de otra forma se produce un giro en el cuerpo. Si esto
ocurre, decimos que la fuerza (cada una) produce una torca t
en el cuerpo dada por: t = F.r.sen q,
donde F es la magnitud de la fuerza, r la distancia del centro de giro del cuerpo
al punto de aplicación de la fuerza y q es el ángulo
que forman r y F.
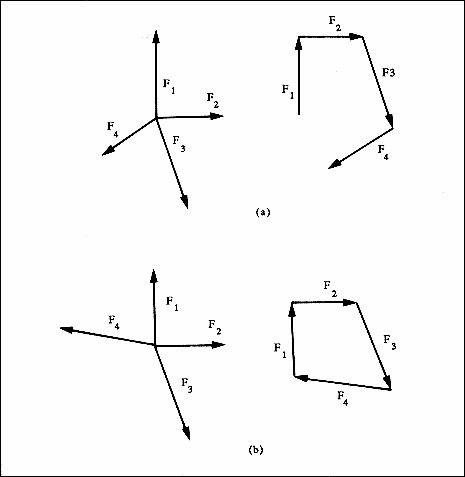
Figura 4. (a) Cuatro vectores de fuerza actuando sobre un objeto, cuya suma por el método gráfico resulta ser diferente del cero, provocan que el cuerpo no esté en equilibrio. (b) Cuatro vectores actuando sobre un cuerpo, cuya suma es cero, provocan que el cuerpo esté en equilibrio.
Por lo anterior, para garantizar que el cuerpo esté en equilibrio, se deben
cumplir simultáneamente dos condiciones: que la suma de las fuerzas actuando
sobre él sea cero y que la suma de las torcas sea cero, es decir: 
y 
.
Lo primero garantiza que no hay movimiento de translación, y lo segundo que
no hay giro o rotación.
Una aplicación de lo anterior, en medicina, es la inmovilización de huesos
rotos, o en sistemas de tracción como el de Russell, que se aplica en caso de
fractura de fémur.
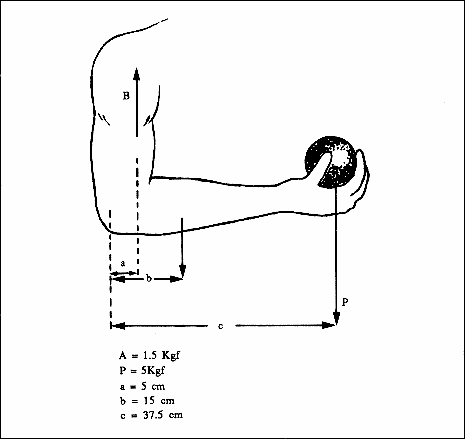
Figura 5. Fuerzas producidas en el antebrazo al sostener un peso P.
Otra aplicación de las condiciones de equilibrio se da en cálculo de la fuerza
ejercida por los músculos, como el bíceps mostrado en la figura 5, donde se
conoce el peso del antebrazo A=1.5 kgf y el peso que sostiene W=5 kgf. Aplicando
la condición de equilibrio: 
y considerando que el centro de giro sería la articulación del codo, se tiene:
que es la fuerza ejercida por el bíceps. Es frecuente que los músculos ejerzan fuerzas mucho mayores que las cargas que sostienen.
Otro concepto importante, si queremos describir el movimiento del cuerpo, es el de centro de gravedad. Éste coincide con el centro geométrico si el cuerpo es perfectamente simétrico y su masa está uniformemente distribuida; en estos casos es fácil calcularlo. De otra forma, lo más fácil es localizarlo experimentalmente, para lo cual basta suspender el cuerpo de tantos puntos como dimensiones tenga, y trazar una línea vertical cada vez; en el punto donde se intersectan estas líneas se encuentra el centro de gravedad.
El concepto de centro de gravedad es útil en terapia física ya que un cuerpo apoyado sobre su centro de gravedad se encuentra en equilibrio y no cambia su posición a menos que actúe una fuerza sobre él. Una persona que está de pie tiene su centro de gravedad en la región pélvica, pero si se dobla hacia delante la localización del centro de gravedad variará, haciendo que la persona gire.
Cuando una persona carga un cuerpo pesado, tiende a moverse en el sentido opuesto al que se encuentra el objeto, para equilibrar el centro de gravedad de los dos juntos: así evita caer.
Cuando varias fuerzas actúan sobre el cuerpo, una forma de simplificar el problema de su movimiento es considerar que todas se aplican en un solo punto, el centro de masa del cuerpo, que puede estar localizado dentro o fuera de éste. El centro de masa es un punto donde teóricamente se concentra toda la masa del cuerpo y está localizado en un punto espacial que nos permite describir el movimiento del cuerpo; por ejemplo, una llanta de coche que rodamos sobre una línea recta: su centro de masa estaría ubicado en el centro, a pesar de no haber masa ahí; dicho punto se mueve en línea recta permitiéndonos describir el movimiento de la llanta del modo más simple posible.
En física consideramos tres casos de equilibrio: estable, inestable e indiferente. El estable es aquél que tiene un cuerpo que al moverse tiende siempre a regresar a su posición original, como sería el caso del péndulo de un reloj: siempre tiende a volver a la posición vertical. El inestable corresponde a aquellos cuerpos que al moverse fuera de su posición de equilibrio no regresan a ella; un ejemplo sería el de un plato sobre un lápiz (malabarismo). El equilibrio indiferente es el de aquellos cuerpos que se mueven de su posición de equilibrio y regresan a la condición de equilibrio en cualquier otra posición, por ejemplo, un hombre que camina, cada vez que se detiene está en equilibrio. El equilibrio es importante para todos los seres vivos, está relacionado con la estabilidad y, en el caso del ser humano, el problema se complica más de lo que puede suponerse porque no se refiere únicamente a la estabilidad física sino también a la estabilidad emocional, acarreando graves consecuencias que generalmente abarcan todo el medio ambiente de la persona, con las consecuencias que esto acarrea.
Cuando un músculo es estimulado, se contrae. Si el músculo se mantiene con longitud constante desarrolla una fuerza, mientras que si mueve un peso se contrae y hace trabajo. Las dos situaciones más simples para estudiar son a) longitud constante (isométrica) y b) fuerza constante (isotónica).
Si el músculo es estimulado por medio de corrientes eléctricas, impulsos mecánicos, calor, frío, etc., ocurre una serie de contracciones, separadas por relajamientos entre cada estímulo. Si los estímulos se repiten antes de que ocurra la relajación, la contracción se mantiene estacionaria; esto se conoce como tétano. Eventualmente todos los músculos sufren de fatiga y su contracción falla cuando haya un estímulo presente.
Es necesario decir que sólo las contracciones isotónicas realizan trabajo. Los músculos estriados en general pueden desarrollar grandes fuerzas para una carga dada, como lo vimos anteriormente, en particular los músculos esqueléticos desarrollan fuerzas mayores que las cargas que soportan; sin embargo, las cargas pueden moverse mucho más de lo que se contrae el músculo.
Cuando un músculo está trabajando produce cierta cantidad de calor debida a la conversión de energía química en trabajo mecánico. Experimentalmente esto se mide a través del aumento en la temperatura del cuerpo. Por lo anterior, una persona que tiene una gran energía puede desarrollar una gran cantidad de trabajo; para tener una gran energía se debe comer bien, ya que la energía química almacenada en los alimentos puede ser completamente transferida al organismo.
La energía de un cuerpo es la capacidad que tiene para desarrollar un trabajo. Desde el punto de vista de la física, existen varias formas de energía: mecánica, química, eléctrica, magnética, etc.; sin embargo, pueden transformarse de una a otra en un sistema como el del organismo humano, por ejemplo. En un sistema aislado (aquél que no tiene interacción con sus alrededores), la energía se transforma sin que exista ninguna pérdida o ganancia en la cantidad total inicial; es por ello que se dice que la energía se conserva. Éste es, quizá, el principio más importante de la física.
Cuando se aplica una fuerza F a un cuerpo de modo que lo desplace una distancia
S, se dice que la fuerza ha desarrollado un trabajo dado por: 
donde q es el ángulo que hace la fuerza F con la
línea de desplazamiento del cuerpo. Si el cuerpo se mueve en la misma línea
en la que se aplica la fuerza, se tiene que el trabajo total realizado es: 
medido en N.m (Newtons por metro) o J (Joules).
Si a un cuerpo, inicialmente en reposo, se le aplica una fuerza constante, es decir una aceleración constante, ya que la fuerza está dada por el producto de la masa del cuerpo por la aceleración que se le imprime: F = m.a; al transcurrir un tiempo t habrá recorrido una distancia
dada por 
de modo que el trabajo estará dado por:
ya que la velocidad se encuentra como v = a.t. A esta cantidad se le conoce como energía cinética del cuerpo, la cual claramente es igual al trabajo desarrollado por él.
La cantidad de trabajo desarrollado por los músculos y las piernas
de un corredor está dado por: 
donde F es la fuerza muscular, S la distancia recorrida en cada zancada del
corredor y m la masa de la pierna. De medidas hechas se sabe que la fuerza es
proporcional al cuadrado de la longitud de la pierna, Lñ, la distancia es proporcional
a L y la masa es proporcional a Lñ de modo que:
este es un resultado interesante ya que nos dice que la velocidad que puede desarrollar un corredor es independiente de su tamaño.
Al caer de una altura h, un cuerpo está sujeto a la acción de la gravedad y
adquiere una velocidad que depende de la constante gravitacional 
,
al sustituirla en la ecuación para la energía cinética se tiene:
que es la energía que tenía almacenada el cuerpo a la altura h, antes de iniciar su caída, y se la conoce como energía potencial del cuerpo.
Muchos de los músculos y huesos del cuerpo actúan como palancas, las cuales se clasifican en tres clases. Las palancas de la primera clase son aquellas en las que el punto de apoyo se encuentra entre el punto de aplicación de la fuerza (en este caso de la fuerza muscular) y el punto de aplicación del peso que se quiere mover; esta clase de palancas son las que menos se presentan en la realidad. Las de segunda clase son aquellas en las que el peso se encuentra entre el punto de apoyo y la fuerza muscular; mientras que en las de tercera clase, que son las más frecuentes, el punto de aplicación de la fuerza muscular se encuentra entre los puntos de aplicación del peso y del apoyo (esto se ilustra en la Figura 6).
Es frecuente que después de cargar un objeto pesado, se sufra de dolor en la
parte baja de la espalda, en la región lumbar, lo que se debe a la mala posición
que se adopta para levantar el peso. Se han hecho medidas de la presión en los
discos que separan las vértebras usando un transductor calibrado conectado a
una aguja hueca que se inserta en el centro gelatinoso de un disco intervertebral
para un adulto que carga un peso adoptando diferentes posiciones: la posición
erecta que adopta la persona sin carga extra provoca una presión en el disco
lumbar de aproximadamente 5 atmósferas; si la carga es de aproximadamente 20
kg, distribuida en igual forma en cada mano a los lados del cuerpo, la presión
alcanza las 7 atmósferas una vez que la persona está erecta. Al momento de levantar
la carga, si la persona dobla las rodillas, la presión alcanzará 12 atmósferas,
mientras que si no las dobla puede llegar hasta 35 atmósferas (1 atm es la presión
ejercida por la atmósfera terrestre al nivel del mar), por lo que es conveniente
doblar las rodillas cada vez que se cargue un peso.
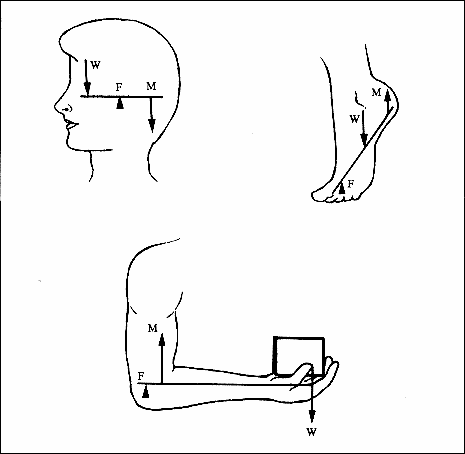
Figura 6. Las tres clases de palancas que se producen en el cuerpo humano.
W es una fuerza que puede ser el peso, M es la fuerza muscular y F la fuerza
de reacción.
