I. LA GRAVITACI�N UNIVERSAL
�POR QU� CAEN LOS CUERPOS Y SE MUEVEN LOS ASTROS?
SEG�N una famosa leyenda, Isaac Newton, sentado bajo un manzano, meditaba sobre la fuerza que mueve a los astros en el cielo, cuando vio caer una manzana al suelo. Este suceso tan trivial fue para �l la clave del problema que le intrigaba: se dio cuenta de que el movimiento de los cuerpos celestes es regido por la misma fuerza que atrae una manzana al suelo: la fuerza de la gravedad. Newton descubri� que la gravitaci�n es un fen�meno universal que no se restringe a nuestro planeta. Aun siendo poco veraz, esta leyenda ilustra uno de los acontecimientos que se�alan el nacimiento de la ciencia moderna: la uni�n de la f�sica celeste con la f�sica terrestre.
Antes de Newton, nadie hab�a sospechado que la gravitaci�n es un fen�meno inherente a todos los cuerpos del Universo. Muy por el contrario, durante la Edad Media y aun hasta tiempos de Newton, se aceptaba el dogma de que los fen�menos terrestres y los fen�menos celestes son de naturaleza completamente distinta. La gravitaci�n se interpretaba como una tendencia de los cuerpos a ocupar su "lugar natural", que es el centro de la Tierra. La Tierra era el centro del Universo, alrededor del cual giraban los cuerpos celestes, ajenos a las leyes mundanas y movidos s�lo por la voluntad divina. Se pensaba que la �rbita de la Luna marcaba la frontera entre la regi�n terrestre y el cielo emp�reo donde las leyes de la f�sica conocidas por el hombre dejaban de aplicarse.
En el siglo XVI, Cop�rnico propuso un sistema helioc�ntrico del mundo seg�n el cual los planetas, incluyendo la Tierra, giraban alrededor del Sol. El modelo de Cop�rnico describ�a el movimiento de los astros con gran precisi�n, pero no ofrec�a ning�n indicio del mecanismo responsable de ese movimiento.
La obra de Cop�rnico fue defendida y promovida apasionadamente por Galileo Galilei. Adem�s de divulgar la hip�tesis helioc�ntrica, Galileo encontr� nuevas evidencias a su favor realizando las primeras observaciones astron�micas con un telescopio; su descubrimiento de cuatro peque�os astros que giran alrededor de J�piter lo convenci� de que la Tierra no es el centro del Universo. Galileo tambi�n fue uno de los primeros cient�ficos que estudiaron la ca�da de los cuerpos, pero es una iron�a de la historia el que nunca sospechara la relaci�n entre la gravedad y el movimiento de los cuerpos celestes. Al contrario, cre�a que los planetas se mov�an en c�rculos por razones m�s est�ticas que f�sicas: el movimiento circular le parec�a perfecto y estable por ser id�ntico a s� mismo en cada punto.
Kepler, contempor�neo de Galileo, descubri� que los planetas no se mueven en c�rculos sino en elipses y que este movimiento no es arbitrario, ya que existen ciertas relaciones entre los periodos de revoluci�n de los planetas y sus distancias al Sol, as� como sus velocidades. Kepler plasm� estas relaciones en sus famosas tres leyes. Una regularidad en el movimiento de los planetas suger�a fuertemente la existencia de un fen�meno universal subyacente. El mismo Kepler sospech� que el Sol es el responsable de ese fen�meno; especul� que alg�n tipo de fuerza emana de este astro y produce el movimiento de los planetas, pero no lleg� a elaborar ninguna teor�a plausible al respecto.
Es justo mencionar que, antes de Newton, el intento m�s serio que hubo para explicar el movimiento de los planetas se debe al cient�fico ingl�s Robert Hooke, contempor�neo de Newton. En 1674, Hooke ya hab�a escrito:
...todos los cuerpos celestes ejercen una atracci�n
o poder gravitacional hacia sus centros, por lo que atraen, no s�lo, sus
propias partes evitando que se escapen de ellos, como vemos que lo hace
la Tierra, sino tambi�n atraen todos los cuerpos celestes que se encuentran
dentro de sus esferas de actividad.* |
Sin esa atracci�n, prosigue Hooke, los cuerpos celestes se mover�an en l�nea recta, pero ese poder gravitacional curva sus trayectorias y los fuerza a moverse en c�rculos, elipses o alguna otra curva.
As�, Hooke intuy� la existencia de una gravitaci�n universal y su relevancia al movimiento de los astros, pero su descripci�n no pas� de ser puramente cualitativa. Del planteamiento prof�tico de Hooke a un sistema del mundo bien fundamentado y matem�ticamente riguroso, hay un largo trecho que s�lo un hombre en aquella �poca pod�a recorrer.
Tal era el panorama de la mec�nica celeste cuando Newton, alrededor de 1685, decidi� atacar el problema del movimiento de los planetas utilizando un poderos�simo formalismo matem�tico que �l mismo hab�a inventado en su juventud —el c�lculo diferencial e integral— logr� demostrar que las tres leyes de Kepler son consecuencias de una atracci�n gravitacional entre el Sol y los planetas.
Todos los cuerpos en el Universo se atraen entre s� gravitacionalmente. Newton descubri� que la fuerza de atracci�n entre dos cuerpos es proporcional a sus masas e inversamente proporcional al cuadrado de la distancia que los separa. As�, si M1 y M2 son las masas de dos cuerpos y R la distancia entre ellos, la fuerza F con la que se atraen est� dada por la f�rmula:
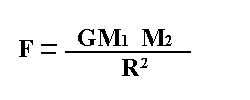
donde G es la llamada constante de la gravitaci�n.
Newton public� sus resultados en su famoso libro intitulado Philosophiae Naturalis Principia Mathematica, cuya primera edici�n data de 1687; la f�sica te�rica hab�a nacido.
La gravitaci�n es el cemento del Universo. Gracias a ella, un planeta o una estrella mantiene unidas sus partes, los planetas giran alrededor del Sol sin escaparse, y el Sol permanece dentro de la V�a L�ctea. Si llegara a desaparecer la fuerza gravitacional, la Tierra se despedazar�a, el Sol y todas las estrellas se diluir�an en el espacio c�smico y s�lo quedar�a materia uniformemente distribuida por todo el Universo. Afortunadamente, la gravedad ha permanecido inmutable desde que se form� el Universo y es una propiedad inherente a la materia misma.
LOS CUERPOS OSCUROS DE LAPLACE
Durante el siglo que sigui� a su publicaci�n, el libro de los Principia fue considerado una obra monumental erigida por su autor para honrar su propia memoria, pero accesible s�lo a unos cuantos iniciados. Se dec�a que Newton hab�a publicado sus c�lculos en forma deliberadamente dif�cil, para que nadie pudiera dudar de la magnitud de su haza�a cient�fica.
Sin embargo, el valor de los Principia era tan evidente que la obra empez� a trascender del estrecho c�rculo de disc�pulos de Newton y lleg� al continente europeo, y muy especialmente a Francia, que se encontraba en aquel entonces en pleno Siglo de las Luces. El escritor y fil�sofo Voltaire visit� Inglaterra durante los �ltimos a�os de vida de Newton, cuando la f�sica del sabio ingl�s se hab�a consolidado plenamente en su patria. Voltaire entendi� la gran trascendencia del sistema newtoniano y se encarg� de introducirlo en Francia; no entend�a de matem�ticas, pero convenci� a su amiga y musa, la marquesa de Le Chatelet, una de las mujeres matem�ticas m�s destacadas de la historia, de que se interesara en la obra de Newton. La marquesa tradujo los Principia al franc�s y, tanto ella como sus colegas Maupertuis, D'Alembert y otros contribuyeron a propagar la nueva ciencia.
Era necesario, sin embargo, reescribir a Newton en un lenguaje matem�tico m�s claro y manejable. La culminaci�n de esta labor qued� plasmada en la gigantesca obra de Pierre-Simon Laplace, publicada en varios vol�menes bajo el t�tulo de Mec�nica celeste, en la que desarroll� todas las consecuencias de la f�sica newtoniana, reformul�ndola en un lenguaje matem�tico que permiti� su subsecuente evoluci�n hasta la f�sica de nuestros d�as.
Con el fin de divulgar su obra, Laplace escribi� una versi�n condensada de la Mec�nica celeste, que public� en 1793, a�o IV de la Rep�blica Francesa, con el t�tulo de El sistema del mundo. En este libro explicaba las consecuencias de la gravitaci�n universal, no s�lo para la estabilidad del Sistema Solar, sino incluso para su formaci�n a partir de una nube primordial de polvo y gas.
En un pasaje particularmente interesante de este libro, Laplace llam� la atenci�n de sus lectores sobre el hecho de que, a lo largo de la historia, muchas estrellas hab�an aparecido s�bitamente y desaparecido despu�s de brillar esplendorosamente durante varias semanas:
Analicemos este pasaje tan notable. Las estrellas vueltas invisibles a las que se refiere Laplace son principalmente las que ahora llamamos supernovas. Como veremos en el cap�tulo III, algunas estrellas pueden explotar bruscamente y volverse extremadamente luminosas durante algunos d�as. Tal fen�meno ha ocurrido en nuestra galaxia al menos unas cuatro veces durante los �ltimos mil a�os; las dos supernovas observadas m�s recientemente ocurrieron en 1572 y 1604. Tambi�n en el cap�tulo III, veremos que una estrella, despu�s de estallar como supernova, arroja gran parte de su masa al espacio interestelar y, su n�cleo que permanece en el lugar de la explosi�n, se vuelve ... �un cuerpo oscuro!
El razonamiento que llev� a Laplace al concepto de un cuerpo que no deja escapar
la luz es bastante simple. Sabemos por experiencia que un proyectil arrojado
verticalmente hacia arriba alcanza una altura m�xima que depende de la velocidad
con la que fue lanzado; mientras mayor sea la velocidad inicial, m�s alto llegar�
antes de iniciar su ca�da. Pero si al proyectil se le imprime una velocidad
inicial superior a 11.5 kil�metros por segundo, subir� y no volver� a caer,
escap�ndose definitivamente de la atracci�n gravitacional terrestre. A esta
velocidad m�nima se le llama velocidad de escape y var�a, de un planeta
o estrella, a otro. Se puede demostrar que la velocidad de escape Vesc
desde la superficie de un cuerpo esf�rico es
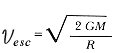
donde M es la masa del cuerpo, R su radio y G la constante de la gravitaci�n que ya tuvimos ocasi�n de conocer.
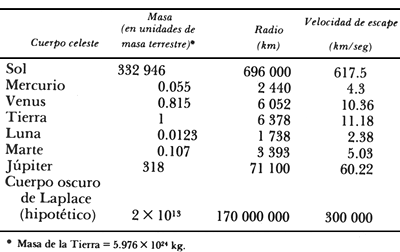
En el cuadro I se dan las velocidades de escape de la superficie de varios cuerpos del Sistema Solar; es importante notar que esta velocidad depende tanto de la masa como del radio del astro.
CUADRO I. La velocidad de escape de la superficie de varios cuerpos celestes.
Esta velocidad depende de la masa y del radio.
Volviendo a Laplace: es posible, al menos en principio, que un cuerpo sea tan masivo o tan compacto que la velocidad de escape de su superficie sea superior a la velocidad de la luz. En ese caso, se podr�a pensar que los rayos luminosos no escapan de ese cuerpo. Este es justamente el argumento que condujo a Laplace a postular la existencia de cuerpos oscuros.
Es f�cil ver de la f�rmula para la velocidad de escape que un cuerpo esf�rico de masa M tendr� una velocidad igual a la de la luz si su radio mide
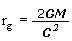
donde c es la velocidad de la luz: 300 000 kil�metros por segundo. El valor rg se llama radio gravitacional y es proporcional a la masa del cuerpo; si el radio de un cuerpo esf�rico es menor que el radio gravitacional, la velocidad de escape de su superficie es superior a la velocidad de la luz.
Un cuerpo oscuro con densidad comparable a la de la Tierra y 250 veces mayor que el Sol tendr�a una masa aproximadamente igual a cien millones de soles. Pero puede haber, en principio, cuerpos oscuros con cualquier masa. El radio gravitacional que corresponde a una masa solar es de 3 kil�metros, lo que implica que si una estrella como el Sol se comprime a ese radio se volver� un cuerpo oscuro en el sentido de Laplace (en comparaci�n, el radio del Sol es de 696 000 kil�metros). El radio gravitacional correspondiente a la misma masa que la de la Tierra es de un cent�metro aproximadamente.
Sin embargo, las consideraciones anteriores s�lo pod�an ser especulativas en la �poca de Laplace. En primer lugar, la f�rmula de la velocidad de escape es v�lida para cualquier part�cula material, independientemente de su masa, pero �se comporta la luz como cualquier part�cula material bajo la acci�n de la gravedad? Esta es una pregunta cuya respuesta era desconocida hasta principios del siglo XX. En segundo lugar, era dif�cil, en tiempos de Laplace, concebir que existieran en el Universo cuerpos cien millones de veces m�s masivos que el Sol, o astros de la masa del Sol comprimidos a un radio de s�lo 3 kil�metros, o un cuerpo tan masivo como la Tierra y del tama�o de una nuez.
Quiz�s fue por estas serias dudas que Laplace elimin� toda menci�n de los cuerpos oscuros de las subsecuentes ediciones de su Sistema del mundo, publicadas en plena restauraci�n borb�nica. Para entonces, su autor se hab�a vuelto el marqu�s de Laplace, y quiz� no juzg� tales especulaciones dignas de un noble y prestigiado cient�fico.
Los cuerpos oscuros permanecieron en la oscuridad hasta el siglo XX, cuando la teor�a de la gravitaci�n de Einstein y la astrof�sica moderna arrojaron nuevas luces sobre ellos.
En el siguiente cap�tulo esbozaremos la teor�a de la relatividad de Einstein, en el contexto de la cual se pueden estudiar los fen�menos relacionados con la luz y la gravedad. En el cap�tulo III veremos c�mo la evoluci�n de una estrella puede conducir, bajo ciertas condiciones, a la formaci�n de un cuerpo que no permite a la luz escapar de su superficie.
NOTAS
* Citado por A. Koyr�, en Newtonian Studies, University of Chicago Press (1965), p. 182
