II. LA TEORÍA DE LA RELATIVIDAD DE EINSTEIN
DURANTE más de dos siglos, la mecánica de Newton dominó completamente en la física: el Universo entero parecía comportarse tal como lo predecían las ecuaciones de la física newtoniana y la comprensión de la naturaleza se había reducido a un problema de técnica matemática. Pero a principios del siglo XX empezaron a surgir evidencias de que la física clásica, así como todos los conceptos relacionados con ella, no describe adecuadamente a los fenómenos que suceden a la escala de los átomos o a velocidades comparables a la de la luz.
La mecánica clásica constituye una excelente aproximación a la realidad, dentro de ciertos límites.Sin embargo en la escala microscópica, los fenómenos físicos sólo pueden estudiarse por medio de la mecánica cuántica. Y cuando se tratan velocidades muy altas, cercanas a la luminosa, se debe recurrir a la teoría de la relatividad.
La primera revolución científica del siglo XX se produjo cuando Albert Einstein (Figura 1) formuló, en 1905, la teoría de la relatividad especial. A continuación describiremos los rasgos esenciales de esta teoría.

Figura 1. Albert Einstein (1879-1955), quien formuló la teoría de la relatividad.
Para estudiar o describir un fenómeno físico debemos recurrir necesariamente a un sistema de referencia con respecto al cual efectuamos mediciones. En la práctica cotidiana el sistema de referencia que más se utiliza, es la Tierra misma que, en general, se supone inmóvil, a pesar de que gira sobre sí misma y alrededor del Sol, recorriendo el espacio cósmico a una velocidad de 30 km/seg. En cambio, para describir el movimiento de los planetas, es más conveniente utilizar al Sol como punto de referencia, o, más precisamente, como centro de un sistema de referencia donde este astro está fijo. Pero ni el Sol, ni las estrellas vecinas a él, se encuentran realmente fijos: el Sol se halla en las regiones externas de una galaxia que rota dando una vuelta completa en millones de años. A su vez, esta galaxia se mueve con respecto a otras galaxias, etcétera.
En la práctica afortunadamente, no es necesario tomar en cuenta todos estos movimientos porque las leyes de la física son las mismas en cualquier sistema de referencia. Este principio fundamental se aplica aun para sistemas de referencia terrestres: en la época de Galileo, los filósofos discutían si una piedra, lanzada desde lo alto del mástil de un barco en movimiento, cae verticalmente con respecto al barco o con respecto a la Tierra. Galileo argumentó que en el sistema de referencia del barco, las leyes de la física tienen la misma forma que en tierra firme y por lo tanto, la piedra cae verticalmente con respecto al barco, aunque éste se mueva.
Así, todo movimiento es relativo al sistema de referencia en el cual se observa y, las leyes de la física, no cambian de un sistema a otro. Este hecho fundamental se conoce como principio de relatividad de Galileo.
Sin embargo, los filósofos y los físicos clásicos veían con desagrado —quizá con vértigo— el hecho de que no existiera un sistema de referencia absoluto con respecto al cual definir todos los movimientos del Universo. Estrictamente hablando, el principio de relatividad no excluye la existencia de tal sistema absoluto, únicamente postula que las leyes de la física son las mismas en ese y en cualquier otro sistema. Pero, a mediados del siglo XIX, surgieron las primeras dificultades de la relatividad galileana, cuando el físico escocés James Clerk Maxwell formuló la teoría matemática de los fenómenos eléctricos y magnéticos.
Maxwell demostró que la electricidad y el magnetismo son dos aspectos de un mismo fenómeno: el electromagnetismo. Como una de las consecuencias más importantes de su teoría descubrió que la luz es una vibración electromagnética que se propaga exactamente como una onda. Pero las ondas lo hacen en medios materiales, por lo que los físicos del siglo pasado postularon la existencia de un medio extremadamente sutil, el éter, que llenaba al Universo entero, permeaba todos los cuerpos y servía de sustento a la luz. Según esta concepción, la luz sería una vibración del éter del mismo modo que el sonido es una vibración del aire.
De existir el éter, sería un sistema de referencia absoluto con respecto al cual medir el movimiento de todos los cuerpos en el Universo. Más aún, se descubrió que las ecuaciones de Maxwell cambian de forma al pasar de un sistema de referencia a otro, lo cual implicaría que el principio de relatividad no se aplica a los fenómenos electromagnéticos. Se postuló, entonces, que estas ecuaciones sólo son válidas en el sistema de referencia del éter en reposo. Esto no es sorprendente pues la luz, fenómeno electromagnético, se propaga con una velocidad bien definida en el éter y esta velocidad debe ser distinta en un sistema de referencia en movimiento con respecto al éter. Al parecer, la teoría electromagnética de Maxwell restituía un sistema de referencia absoluto.
La manera más evidente de confirmar las ideas anteriores es medir la velocidad de la luz, emitida en direcciones opuestas, en la Tierra: la diferencia de velocidades puede llegar a ser tan grande como 60 km/seg (Figura 2). Esta velocidad es muy pequeña con respecto a la velocidad total de la luz, que es de 300 000 km/seg, pero, a fines del siglo pasado, los físicos experimentales Michelson y Morley lograron construir un aparato que permitía medir diferencias aún más pequeñas en la velocidad de un rayo luminoso. Michelson y Morley realizaron su experimento en 1887: para sorpresa de la comunidad científica de esa época, no detectaron ningún cambio de la velocidad de la luz. Esta velocidad era la misma en cualquier dirección, independientemente de cómo la Tierra se mueva con respecto al hipotético éter.
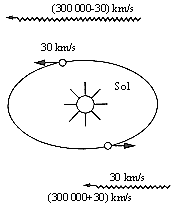
Figura 2. Aparentemente, la velocidad de la luz debería cambiar según la dirección en que se mueve, debido a la velocidad de la Tierra en el espacio.
Se hicieron muchas especulaciones sobre el resultado negativo del experimento: quizá la Tierra arrastra el éter consigo, quizá los objetos materiales se contraen en la dirección de movimiento con respecto al éter... Finalmente, Einstein encontró la solución al problema.
Para empezar, Einstein postuló que las ecuaciones de Maxwell del electromagnetismo son rigurosamente válidas en cualquier sistema de referencia. Esta condición de invariancia se cumple a condición de que el tiempo medido en un sistema no coincida con el medido en otro sistema. Este hecho no había sido tomado en cuenta por los antecesores de Einstein y, por esta razón, las ecuaciones de Maxwell parecían violar el principio de relatividad.
Habiendo postulado que no puede haber ningún sistema de referencia privilegiado, Einstein concluyó que el éter simplemente no existe. Pero, entonces ¿con respecto a qué debe medirse la velocidad de la luz? La respuesta de Einstein fue drástica: la velocidad de la luz es la misma en cualquier sistema de referencia. Después de todo, eso es lo que indica el experimento de Michelson y Morley.
Este concepto de la invariancia de la velocidad de la luz contradice nuestro "sentido común". Si la velocidadd de la luz es de 300 000 km/seg, esperaríamos que al perseguir una señal luminosa veamos que se mueve con una velocidad menor. (Si, por ejemplo, corremos a 80 km/hora detrás de un tren que se mueve a 100 km/hora, vemos que el tren se mueve con respecto a nosotros a 20 km/hora.) Sin embargo, debido a la no invariancia del tiempo, las velocidades no se adicionan o sustraen en el caso de señales luminosas (o, en general, de partículas que se mueven casi tan rápidamente como la luz).
Los efectos predichos por la teoría de la relatividad son imperceptibles en nuestra vida cotidiana y sólo se manifiestan cuando se involucran velocidades comparables a la de la luz. Consideremos, como ejemplo, una nave espacial que se mueve con una velocidad muy alta: despega de la Tierra y regresa después de recorrer cierta distancia. Según la relatividad, el tiempo transcurre normalmente tanto para los que se quedaron en la Tierra como para los pasajeros de la nave, pero esos dos tiempos no son iguales. Al regresar a la Tierra, los tripulantes de la nave constatarán que el viaje duró para ellos un tiempo menor que para los que se quedaron. Más precisamente, el tiempo medido en la nave es más pequeño que el medido en la Tierra por un factor de acortamiento
donde v es la velocidad de la nave y c la velocidad de la luz.1
Para velocidades v del orden de algunos metros o kilómetros por segundo, como las que ocurren comúnmente en nuestras experiencias diarias, el factor de acortamiento es tan cercano al valor 1 que es imposible detectar el efecto relativista del cambio de tiempo. Si la nave espacial viaja a unos 10 000 km/hora, la diferencia entre los tiempos medidos será apenas una diez millonésima de segundo por cada hora transcurrida (lo cual, incidentalmente, se ha podido confirmar con la tecnología moderna). Pero, en el otro extremo, si la nave viaja a una velocidad muy cercana a la de la luz, su tiempo puede ser muy corto con respecto al transcurrido en la Tierra: por ejemplo, a la velocidad de 295 000 km/seg, una nave espacial tardaría unos 20 años medidos en la Tierra para ir a la estrella Sirio y regresar; sin embargo, para los tripulantes de la nave habrán pasado ¡sólo 3 años y medio!
La contracción del tiempo no es el único efecto sorprendente que predice la teoría de la relatividad. Einstein también demostró que existe una equivalencia entre la energía y la masa, dada por la famosa fórmula
E= mc2
donde E es la energía equivalente a una masa m de materia. Por ejemplo, el núcleo de un átomo de helio está constituido por dos protones y dos neutrones, pero la masa del núcleo de helio es un poco menor, cerca del 4%, que la masa sumada de dos protones y dos neutrones separados (Figura 3); en consecuencia, al unirse estas cuatro partículas pierden una fracción de masa que se transforma en energía; éste es el principio de la fusión nuclear, que permite brillar al Sol y a todas las estrellas (y construir bombas atómicas).
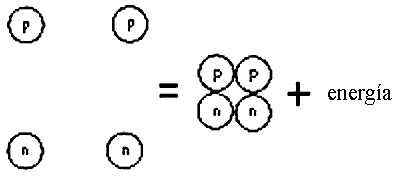
Figura 3. Un núcleo de helio pesa menos que sus componentes por separado: dos protones y dos neutrones. Al formarse un núcleo de helio, la diferencia de masa se libera en forma de energía (fusión nuclear).
De la fórmula E = mc² no se deduce que cualquier masa se puede transformar en energía o viceversa; este proceso se da sólo en condiciones muy particulares. Hemos mencionado la fusión nuclear, pero la manera más eficiente de transformar masa en energía es por la aniquilación de la materia con la antimateria2
Al entrar en contacto una partícula con su correspondiente antipartícula, las dos se aniquilan totalmente quedando sólo energía en forma de rayos gamma: la eficiencia de este proceso de transformación de materia en energía es del 100%. En el siguiente capítulo veremos que, bajo circunstancias muy especiales, la gravitación puede ser un mecanismo de liberación de energía más eficiente que la fusión nuclear y sólo superado por la aniquilación de materia y antimateria.
Para aumentar la velocidad de un cuerpo, hay que proporcionarle energía, lo cual se manifiesta como un aumento de la masa del cuerpo. La teoría de la relatividad predice que la energía necesaria para que un cuerpo de masa m alcance la velocidad v es
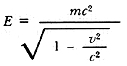
En el límite v = 0, se recupera la fórmula E = mc² para la energía ya existente en forma de masa. En el otro extremo, la energía E aumenta con la velocidad (Figura 4) y se necesita una energía infinita para que el cuerpo alcance la velocidad de la luz. Es por ello que, según la teoría de la relatividad, ningún cuerpo puede alcanzar o superar la velocidad de la luz. La excepción es la luz misma: según la física moderna la luz está constituida por unas partículas llamadas fotones, la masa de un fotón es nula y, por ello, puede viajar a la velocidad límite c.
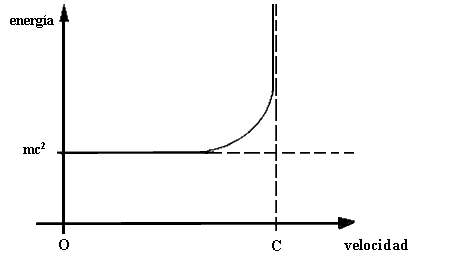
Figura 4. La energía de un cuerpo en movimiento aumenta con su velocidad.
Así, según la teoría de la relatividad, la velocidad de la luz es una barrera fundamental de la naturaleza que no puede ser superada. Se ha especulado sobre la existencia de posibles partículas que se mueven más rápidamente que la luz, los hipotéticos taquiones, pero nunca se ha encontrado alguna evidencia de que sean reales; más aún, de existir, se producirían situaciones contradictorias, como por ejemplo, poder regresar en el tiempo.
En la teoría de Einstein, el espacio y el tiempo dejan de ser categorías independientes como en la física clásica, para fundirse en un concepto unificado: el espacio-tiempo, en el que el tiempo aparece como una cuarta dimensión. A primera vista, puede parecer que este concepto desborda el marco del sentido común, pero en realidad no hay nada de misterioso en él. Si queremos describir la posición de un objeto, necesitamos un sistema de referencia y tres números, llamados coordenadas, porque el espacio tiene tres dimensiones. Por ejemplo, podemos localizar un avión si especificamos la longitud y la latitud del lugar donde se encuentra así como su altura sobre el nivel del mar; con estos tres datos se determina exactamente su posición con respecto al sistema de referencia que es la Tierra. Sin embargo, como el avión se mueve, también conviene precisar en qué momento se encontraba en la posición indicada. Al especificar también el tiempo, estamos describiendo un suceso, algo que ocurre en un lugar dado (descrito por 3 coordenadas) y en un cierto instante (descrito por el tiempo). Nada nos impide interpretar formalmente el tiempo como una cuarta coordenada e introducir así, el concepto del espacio-tiempo: un espacio de cuatro dimensiones, tres espaciales y una temporal. Un punto de ese espacio-tiempo será un suceso, especificado por cuatro coordenadas.
Hasta aquí, el concepto de un espacio-tiempo parece ser bastante trivial. Sin embargo, en el marco de la teoría de la relatividad cobra una estructura insospechada que fue descubierta por el matemático alemán Herman Minkowski.
Empecemos considerando un espacio de dos dimensiones: por ejemplo, una superficie plana. Podemos describir cualquier punto del plano si fijamos un sistema de referencia que, en el caso más simple, puede ser un par de ejes rectos perpendiculares entre sí. Dado un punto cualquiera, llamemos x a la distancia de ese punto al eje vertical y y a la distancia al eje horizontal (Figura 5). Es obvio que si especificamos el valor de x y y, estamos determinando un punto: en este caso, x y y son las coordenadas. Sólo hay dos porque el espacio ahora considerado tiene dos dimensiones.
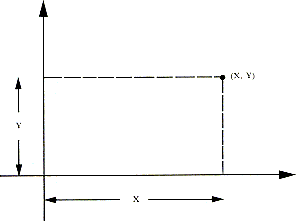
Figura 5. La posición de un punto en un plano con respecto a un sistema de referencia se determina por medio de dos coordenadas x y y.
Sean ahora dos puntos, con coordenadas (x, y) la primera y (x + dx, y + dy) la segunda. Si llamamos ds la distancia entre esos dos puntos, entonces, según el teorema de Pitágoras, el cuadrado de esa distancia está dado por la fórmula
como puede verse en la figura 6.
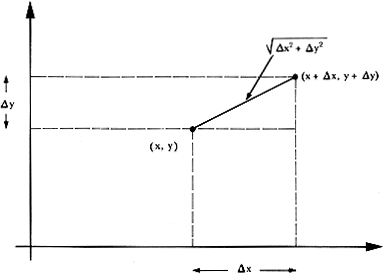
Figura 6. La distancia entre dos puntos se determina con la fórmula para medir distancia.
Las consideraciones anteriores pueden extenderse a un espacio de tres dimensiones:
en este caso, se necesitan tres coordenadas x, y, z para precisar
un punto (figura 7). El cuadrado de la distancia entre el punto con coordenadas
(x, y, z) y el punto con coordenadas (x + dx, y + dy, z
+ dz) es
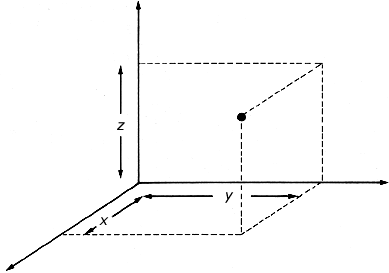
Figura 7. En el espacio de 3 dimensiones, se necesitan tres coordenadas (x, y, z) para determinar la posición de un punto con respecto a un sistema de coordenadas.
Ahora, volvamos al espacio-tiempo de cuatro dimensiones. De las consideraciones
anteriores podemos especificar un suceso con cuatro coordenadas: x , y,
z, t; los tres primeros determinan la posición del suceso
y el último fija el momento en que ocurrió. En la teoría de la relatividad,
se puede definir una seudodistancia (al cuadrado) entre dos sucesos con
coordenadas (x, y, z, t) y (x + dx, y + dy, z + dz, t +
dt) de acuerdo con la fórmula
ds² = dx² + dy² + dz² - c² dt²
(recordemos que c es la velocidad de la luz).
¿Por qué esta forma, con un signo negativo frente al último término? La razón es que la distancia entre dos puntos debe poseer una propiedad fundamental: ser invariante con respecto a cambios del sistema de referencia usado: una barra no cambia su longitud real porque la miremos de lado, de frente o de cabeza. En el caso del espacio-tiempo, la seudodistancia definida arriba tiene una propiedad fundamental: es invariante al pasar de un sistema de referencia a otro. Si consideramos dos sucesos S1 S2 que ocurren uno después del otro, la seudodistancia entre ellos no depende de quién los mida —del mismo modo que la distancia entre las puntas de una barra es invariante—. La interpretación física de la seudodistancia es muy simple: supongamos que un observador se mueve con velocidad constante de tal modo que, para él, los dos sucesos S1 S2 ocurren en el mismo lugar; el tiempo que mide entre esos dos sucesos es precisamente la seudodistancia entre ellos: este es el tiempo propio entre S1 S2 y así lo llamaremos de ahora en adelante, en lugar de seudodistancia. El tiempo propio es un invariante en el espacio-tiempo y es una cantidad perfectamente bien definida. La relatividad no excluye la posibilidad de determinar, en forma única, el tiempo propio medido por un observador, en contra de lo que a veces se entiende, erróneamente, por la palabra relatividad.
El espacio-tiempo en el que las "distancias", o tiempos propios, se miden según
la fórmula
es el llamado espacio de Minkowski. Veremos más adelante que la fórmula para medir "distancias" tiene un papel fundamental tanto en la teoría de relatividad especial, como en la general.
LA TEORÍA DE LA RELATIVIDAD GENERAL
La relatividad especial surgió de una comprensión global de las fuerzas electromagnéticas. Sin embargo, existe en la naturaleza otro tipo de fuerza, la gravitación, cuya descripción no cabe dentro de la teoría de la relatividad especial. Como vimos anteriormente, la mecánica clásica es el fundamento de la teoría newtoniana de la gravitación, pero, en casos extremos, esta mecánica es incompatible con la relatividad especial. Era necesario, pues, crear una teoría relativista de la gravitación, que incluyera, por una parte, la teoría newtoniana en el límite de velocidades pequeñas y, por otra, a la relatividad especial en el caso especial en que la fuerza gravitacional tenga efectos despreciables. Éste es el formidable problema que atacó Einstein desde 1905, cuando presentó su teoría especial, hasta 1915, cuando publicó la versión definitiva de la teoría de la relatividad general.
Para incluir a la gravedad en una teoría relativista, Einstein desafió una vez más al sentido común al postular que el espacio-tiempo es curvo y la gravedad es la manifestación de esa curvatura.
Para entender la idea de un espacio-tiempo curvo, empecemos considerando el caso más simple de un espacio de dos dimensiones curvo: por ejemplo, la superficie de una esfera. Es evidente que no se puede trazar una línea recta sobre tal superficie; sin embargo, si recordamos que la línea recta es la trayectoria de menor longitud entre dos puntos dados, podemos generalizar el concepto y definir una curva de longitud mínima sobre una superficie curva; en el caso de la esfera, esa curva es una porción de arco (Figura 8). En términos técnicos, las curvas de menor longitud sobre una superficie curva se llaman geodésicas.
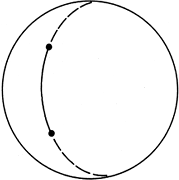
Figura 8. Sobre la superficie de una esfera, la geodésica —curva de menor longitud entre dos puntos— es un segmento de arco.
Sobre un plano, las geodésicas son líneas rectas que, como se enseña en las clases de geometría, satisfacen toda una serie de condiciones: dos rectas que se cruzan en un punto no vuelven a cruzarse en otro, un par de rectas paralelas nunca se cruzan, etc. Sin embargo, estas condiciones no son satisfechas por las geodésicas en general: sobre la superficie de una esfera, dos geodésicas se cruzan en dos puntos, un par de geodésicas aparentemente paralelas se cruzan, etc. (Figura 9).
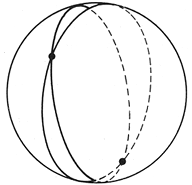
Figura 9. Dos geodésicas "paralelas" se cruzan en dos puntos.
Más aún, la fórmula para medir distancias sobre una superficie curva, toma
ahora una forma más complicada que la presentada anteriormente (ds² =
dx² + dy²). Sobre la superficie de la Tierra se necesitan dos coordenadas,
la longitud y la latitud, para especificar completamente la posición de un punto.
Si un punto tiene longitud ![]() y latitud
y latitud ![]() y,
otro punto tiene longitud
y,
otro punto tiene longitud ![]() y latitud
y latitud ![]() ,
la distancia ds entre esos dos puntos está dada por la fórmula
,
la distancia ds entre esos dos puntos está dada por la fórmula
![]()
donde r es el radio terrestre. 3
El hecho de que la distancia se calcula en forma distinta sobre una superficie curva que sobre una plana equivale, intuitivamente, a un hecho muy simple: no se puede aplanar una superficie curva sin deformar las distancias reales, lo cual es un problema bien conocido por los que elaboran o usan mapas.
Una superficie posee dos dimensiones y es fácil visualizar una superficie curva. En el siglo XIX, algunos matemáticos, como el ruso Lobashevski y el alemán Riemann, se preguntaron si el concepto de superficie curva no podría extenderse a los espacios, "curvos" de tres dimensiones. En tales espacios los postulados básicos de la geometría clásica no se cumplirían: las rectas podrían cruzarse en más de un punto, las paralelas no mantendrían entre sí la misma distancia, etc. En particular, Riemann (Figura 10) tuvo la idea de definir un espacio curvo con cualquier número de dimensiones: cada punto de un espacio de n dimensiones (n es un número entero cualquiera: 1, 2, 3, 4, etc.) se localiza por medio de un conjunto de n coordenadas.

Figura 10. Georg Friedrich Bernhard Riemann (1826-1866). Su concepción del espacio revolucionó la física y las matemáticas.
Riemann demostró que las propiedades básicas de un espacio curvo están determinadas exclusivamente por la fórmula para medir "distancias". Cada forma de ds² define un cierto espacio riemanniano, en el que las líneas rectas pierden sentido, pero son sustituidas por curvas geodésicas cuya longitud —medida según ds²— es mínima.
A diferencia de las superficies, que son espacios de dos dimensiones, los espacios curvos de tres o más dimensiones simplemente no se pueden visualizar. Sin embargo, es posible definirlos y manejarlos matemáticamente sin ninguna dificultad formal; los espacios riemannianos son un excelente ejemplo de un concepto que sólo se puede describir en el lenguaje matemático.
Durante muchos años, los espacios riemannianos fueron considerados como simples curiosidades matemáticas, ajenas a la realidad. No fue hasta la segunda década del siglo xx cuando Albert Einstein se dio cuenta de que, para incluir la gravitación en la teoría de la relatividad, era necesario admitir que el espacio-tiempo es un espacio de Riemann. Einstein llegó a tal conclusión a partir de una serie de brillantes deducciones lógicas y, con la ayuda de su amigo el matemático Marcel Grossman que le había despertado el interés en los trabajos de Riemann, se propuso formular matemáticamente una teoría relativista de la gravitación. Después de varios intentos, Einstein publicó la versión definitiva de la teoría de la relatividad general en el número de noviembre de 1915 del Boletín de la Academia de Ciencias de Berlín, en plena primera Guerra Mundial.
La esencia de la teoría de la relatividad general es que el espacio-tiempo es curvo. En ausencia de masas gravitantes se tiene un espacio-tiempo de Minkowski y una partícula se mueve en línea recta porque nada influye sobre su trayectoria. La presencia de una masa deforma al espacio-tiempo y el concepto de recta pierde su sentido; en un espacio-tiempo curvo, una partícula se mueve a lo largo de una geodésica. Según esta interpretación, un planeta gira alrededor del Sol porque sigue una trayectoria geodésica en el espacio-tiempo deformado por la masa solar.
¿Por qué nadie antes de Einstein se había percatado de que vivimos en un espacio curvo? La razón es que la curvatura inducida por la gravedad de la Tierra o la del Sol es extremadamente leve. La situación se asemeja a la de los antiguos hombres que creían que la Tierra era plana ya que la curvatura terrestre es imperceptible a pequeña escala. Los efectos de la curvatura del espacio-tiempo se manifiestan plenamente a escala del Universo mismo,4 o cerca de objetos cuya atracción gravitacional sea extremadamente intensa.
En un espacio-tiempo de Minkowski, la seudodistancia o tiempo propio se mide según la fórmula ds² = dx² + dy² + dz² - c² dt² pero en un espacio-tiempo riemanniano, la fórmula para ds² toma una forma más general determinada por la distribución de masa. En la teoría newtoniana, se puede calcular matemáticamente la atracción gravitacional ejercida por una distribución dada de masa. En la teoría de Einstein, la situación es bastante más complicada porque no sólo la masa sino también la energía ejerce una acción gravitacional. En su artículo de 1915, Einstein dedujo la fórmula matemática que relaciona la geometría del espacio-tiempo con la distribución de masa y energía: esta fórmula se conoce como ecuación de Einstein y es el corazón de la teoría de la relatividad general (Figura 11).
Figura 11. La ecuación de Einstein. El lado izquierdo describe la geometría del espacio-tiempo y el lado derecho representa la distribución de materia y energía.
En principio, dado un cuerpo con cierta forma y velocidad, se puede calcular su distribución de masa y energía, a partir de la cual, utilizando la ecuación de Einstein, se puede calcular la ds² que determina enteramente la estructura del espacio-tiempo curvo. En la práctica, este procedimiento es extremadamente complicado, porque la ecuación de Einstein, que en realidad es un conjunto de diez ecuaciones, es imposible de resolver exactamente, excepto en algunos casos particulares.
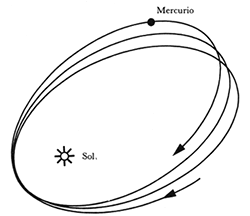
Al principio, Einstein logró resolver en forma aproximada su ecuación y, aun así, obtuvo resultados sumamente interesantes. En primer lugar, demostró que un planeta no describe una elipse perfecta al girar alrededor del Sol, sino una cuasi-elipse, cuyo perihelio se corre lentamente (Figura 12). Este efecto había sido observado en el planeta Mercurio sin que los astrónomos hubieran podido explicarlo con base en la teoría newtoniana. El primer éxito de la relatividad general fue precisamente deducir el valor exacto del corrimiento del perihelio de Mercurio.
El segundo efecto importante que predijo Einstein es que la trayectoria de la luz, al igual que la de un proyectil, debe desviarse por la atracción gravitacional de un cuerpo masivo. Al contrario de la teoría de Newton, la relatividad general sí predice cómo se mueve la luz bajo la acción de la gravedad. Einstein calculó que un rayo luminoso debe desviarse un ángulo de 1.75 segundos de arco al pasar cerca del Sol (Figura 13), lo cual podría comprobarse determinando la posición aparente de una estrella cercana al disco solar durante un eclipse. Esta observación fue realizada por el astrofísico inglés A. S. Eddington al término de la primera Guerra Mundial, confirmando la predicción de Einstein.
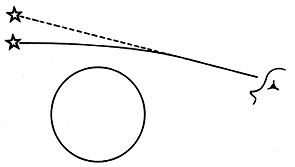
Figura 13. Desviación de un rayo luminoso al pasar cerca del Sol.
Es un hecho notable que la primera solución exacta de la ecuación de Einstein, que corresponde a un caso físico real, fue descubierta sólo unos meses después de que apareciera el famoso artículo de 1915. Esta solución se debe a Karl Schwarzschild, un notable astrónomo alemán que contaba, entre sus trabajos científicos, los primeros estudios teóricos de los procesos radiativos en las estrellas, aplicaciones de la fotografía a la astronomía, una teoría pionera de los espectros atómicos, etc. Al estallar la primera Guerra Mundial, Schwarzschild fue movilizado por el ejército prusiano al frente oriental. Ahí, en condiciones precarias, contrajo una enfermedad infecciosa mortal, por lo que se le permitió regresar a su casa. Fue literalmente en su lecho de muerte donde leyó el artículo de Einstein de noviembre de 1915. Las ecuaciones parecían extremadamente complicadas, pero Schwarzschild tuvo la idea de considerar un problema simple, aunque realista: ¿Cómo deforma al espacio-tiempo una distribución perfectamente esférica de masa? Evidentemente, el espacio-tiempo resultante debe tener propiedades simetricas alrededor de la masa considerada; esto simplifica notablemente las ecuaciones, a tal grado que encontró una solución exacta: el espacio-tiempo de Schwarzschild, un espacio riemanniano que describe la región externa de un cuerpo esférico con masa M y radio arbitrario. (La fórmula para el tiempo propio tiene la forma que se muestra en la figura 14.) Las partículas se mueven en este espacio-tiempo a lo largo de geodésicas, lo cual se reduce, en primera aproximación, justamente a las trayectorias predichas por la mecánica de Newton.
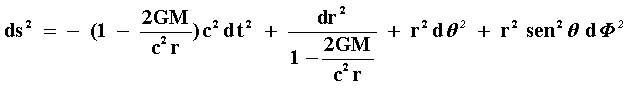
Figura 14. La solución de Schwarzschild.
El resultado obtenido por Schwarzschild fue publicado en julio de 1916, dos meses después de la muerte de su autor. Durante varias décadas, fue prácticamente el único ejemplo, junto con los modelos cosmológicos,5 de una solución de la ecuación de Einstein que corresponde a una situación física real.
En el capítulo V estudiaremos con más detalles el espacio-tiempo de Schwarzschild. Por ahora sólo mencionaremos un hecho importante: si la esfera considerada de masa M tiene un radio menor que el radio de Schwarzschild.
entonces algo extraño sucede: la luz emitida de su superficie, o de cualquier punto dentro de la esfera con radio r, no puede llegar al radio crítico y queda atrapada para siempre. Ésta es exactamente, la situación descrita por Laplace y es un hecho notable que el valor del radio gravitacional, calculado heurísticamente según la mecánica clásica, corresponde exactamente al valor del radio de Schwarzschild.
En la terminología moderna, los cuerpos oscuros de Laplace son los hoyos negros. Corresponden al espacio-tiempo producido por un cuerpo masivo cuyo tamaño es igual o menor que su radio de Schwarzschild. La superficie esférica cuyo radio es justamente el de Schwarzschild se llama horizonte del hoyo negro; la luz puede cruzar el horizonte sólo en un sentido: de afuera hacia adentro y nunca al revés. Lo que ocurre dentro del horizonte está eternamente desconectado del exterior, no puede ser visto ni puede influir sobre el resto del Universo.
NOTAS
1 Por simplicidad, suponemos que el tiempo que tarda la nave en despegar, dar vuelta y aterrizar es despreciable.
2 A cada partícula de materia, como el protón, el neutrón y el electrón, corresponde una antipartícula con signo (y otras propiedades) contrario: el antiprotón, el antineutrón, el positrón...
3 Estrictamente hablando, la formula anterior es válida para una distancia infinitesimal. Los lectores familiarizados con el cálculo diferencial e integral habrán reconocido la "diferencial de distancia", a partir de la cual se puede calcular la longitud de una curva arbitraria por medio de una integración.
4 Ver El descubrimiento del Universo, S. Hacyan, núm. 6 de La Ciencia desde México, FCE, 1986.
5 S. Hacyan, op. cit.