III. LA MUERTE DE LAS ESTRELLAS
LAS estrellas, como todos los cuerpos materiales del Universo, est�n constituidas por �tomos.
Un �tomo consta de un n�cleo, con carga el�ctrica positiva, rodeado de electrones, con cargas el�ctricas negativas. A su vez, un n�cleo at�mico est� formado por dos tipos de part�culas: protones, cargados positivamente y neutrones, sin carga (Figura 15).
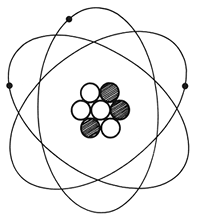
Figura 15. Un �tomo de litio. El n�cleo est� formado por 3 protones y 4 neutrones. En estado neutro, el �tomo posee 3 electrones.
El calor es una manifestaci�n macrosc�pica del movimiento de los �tomos. Mientras m�s caliente est� un cuerpo, sus �tomos se mueven m�s r�pido, chocando continuamente entre s�. Si la temperatura es muy alta, los �tomos llegan a "sacudirse" de algunos o de todos sus electrones: se forma, entonces, una mezcla de n�cleos at�micos y de electrones libres.
Una estrella es una gigantesca masa de gas incandescente que brilla porque en su centro se producen reacciones de fusi�n nuclear. La temperatura en el centro de una estrella puede alcanzar decenas de millones de grados.1 A tales temperaturas, los n�cleos, desprovistos de electrones, chocan tan violentamente unos con otros que llegan a fusionarse entre s�. Al principio son los n�cleos de hidr�geno los que se fusionan para producir n�cleos de helio. Como vimos en el cap�tulo anterior, la masa del n�cleo de helio es ligeramente inferior a la masa de sus constituyentes por separado y la diferencia se libera en forma de energ�a. Este proceso genera la energ�a que radia una estrella —el Sol, por ejemplo— en forma de luz y calor.
En la plenitud de su vida, una estrella se mantiene en equilibrio gracias al balance muy preciso entre dos fuerzas que act�an sobre ella: la fuerza de atracci�n gravitacional entre las diversas partes de la estrella y la fuerza de presi�n de la materia incandescente. La primera fuerza tiende a contraer a la estrella y la segunda a expanderla (recordemos que un gas, al calentarse, se expande aumentando su presi�n). En la mayor�a de las estrellas, el equilibrio entre estas dos fuerzas puede durar miles de millones de a�os. Los astr�nomos han calculado que el Sol naci� hace unos cinco mil millones de a�os y seguir� brillando, en la forma en que lo hace actualmente, durante otro lapso semejante.
El combustible nuclear de una estrella no puede durar eternamente. Cuando todo el hidr�geno del centro de la estrella se ha transformado en helio, pueden suceder otras reacciones nucleares en las que est�n involucrados otros elementos qu�micos. As�, si la temperatura en el centro de la estrella alcanza unos doscientos millones de grados, los n�cleos de helio se fusionan entre s� y producen n�cleos de ox�geno y carbono. Si aumenta a�n m�s la temperatura, el carbono se trasmuta en ox�geno, ne�n, sodio y magnesio, y as� sucesivamente. Si la temperatura central alcanza unos 3 000 millones de grados, se pueden formar todos los n�cleos at�micos que no sean m�s pesados que el hierro, pues los elementos m�s pesados que �ste no pueden fusionarse liberando energ�a, as� que la fusi�n nuclear en una estrella se termina definitivamente cuando s�lo queda hierro en su centro. De hecho, en la mayor�a de las estrellas, la fusi�n nuclear termina mucho antes, pues s�lo las estrellas m�s masivas son lo suficientemente calientes como para producir hierro.
La evoluci�n final de una estrella es un proceso bastante complicado, en el que fases de expansi�n, equilibrio y compresi�n pueden alternarse varias veces a medida que la estrella quema diversos tipos de combustible nuclear en su centro. Relacionadas con las etapas evolutivas de la estrella, se producen inestabilidades que originan desde la expansi�n de las capas gaseosas m�s externas, hasta la eyecci�n violenta de grandes cantidades de materia estelar al espacio. En cualquier caso, al envejecer, las estrellas arrojan al espacio una fracci�n importante de sus masas, con lo que enriquecen de gas el medio interestelar. De ese gas se forman nuevas estrellas, en un proceso que se repite desde hace miles de millones de a�os.
No todas las estrellas viven y mueren de la misma manera; el par�metro fundamental que determina la evoluci�n de una estrella es su masa. La masa de nuestro Sol es aproximadamente 2 000 000 000 000 000 000 000 000 000 000 kilogramos o, escrito en forma m�s compacta 2X1030 kg (es decir, 2 seguido de 30 ceros). El Sol es una estrella de un tipo bastante com�n. La masa de las estrellas puede variar en un rango muy amplio; desde una cent�sima hasta cien veces la masa del Sol. Una estrella no puede tener menos de una cent�sima de la masa solar porque la temperatura en su centro ser�a insuficiente para encender las reacciones nucleares; y una estrella cien veces m�s masiva que el Sol ser�a sumamente inestable y se desbaratar�a r�pidamente.
Por supuesto, las estrellas m�s masivas disponen de m�s materia para liberar energ�a y, por lo tanto, brillan m�s que las poco masivas. Sin embargo, mientras m�s masiva es una estrella, menos tiempo brilla, porque consume su combustible nuclear mucho m�s r�pidamente que una estrella poco masiva. Los astrof�sicos han calculado que las estrellas m�s masivas derrochan toda su energ�a en unas cuantas decenas de miles de a�os, mientras que una estrella como el Sol puede brillar tranquilamente durante 10 000 millones de a�os.
En la actualidad, la mayor�a de los astr�nomos piensa que las estrellas se forman a partir de condensaciones en las gigantescas nubes de gas observadas en la galaxia. Por otra parte, debemos recordar que, seg�n las teor�as cosmol�gicas m�s aceptadas, el Universo mismo naci� hace unos 15 mil millones de a�os y que la edad de nuestra galaxia —de la que forma parte el Sol y todas las estrellas que observamos— es muy cercana a la del Universo.2
Ahora bien, se ha calculado que las estrellas cuya masa es inferior a unas 0.7 veces la masa del Sol, pueden vivir por m�s de 15 mil millones de a�os, mientras que, como ya se�alamos, las m�s masivas apenas viven unas cuantas decenas de miles de a�os. En consecuencia, podemos afirmar con certeza que deben existir en nuestra galaxia much�simos restos de estrellas m�s masivas que 0.7 masas solares, que ya dejaron de brillar o est�n en las �ltimas etapas de su evoluci�n. Es aqu� donde surge la pregunta: �qu� aspecto tienen estas estrellas que dejaron de brillar? Dependiendo de la masa de la estrella, o lo que queda de ella, su fin puede tomar tres formas distintas: enana blanca, estrella de neutrones y hoyo negro.
A principios de los a�os veinte, los astr�nomos hab�an descubierto tres estrellas de muy baja luminosidad y de un color claramente blanco. La m�s notable era una peque�a, visible s�lo con telescopio, que giraba alrededor de Sirio, la estrella m�s brillante del firmamento. A partir del periodo de revoluci�n de esta estrella alrededor de Sirio, los astr�nomos calcularon que la masa de la peque�a compa�era no exced�a una masa solar, pero otras observaciones indicaron que su radio era de unos 20 000 kil�metros (apenas el triple del radio terrestre), un tama�o inusitadamente peque�o para una estrella. Estos valores de la masa y el radio implicaban que la compa�era de Sirio deb�a ser un cuerpo extremadamente compacto: una cucharada de su materia pesar�a cerca de 100 kilogramos.
Los astrof�sicos dedujeron correctamente que las estrellas de este tipo, a las que bautizaron "enanas blancas", se encuentran en la etapa final de su evoluci�n. Al agotar una estrella su combustible nuclear, la presi�n interna no puede contrarrestar su propia fuerza gravitacional y la estrella se contrae hasta alcanzar una nueva configuraci�n de equilibrio, en la que la materia adquiere caracter�sticas completamente nuevas, determinadas por las leyes de la mec�nica cu�ntica que rigen el mundo at�mico. A continuaci�n, abriremos un par�ntesis para describir este estado de la materia.
Poco despu�s del surgimiento de la mec�nica cu�ntica, el f�sico suizo Wolfgang Pauli descubri� que una ley fundamental de la naturaleza proh�be a dos o m�s electrones ocupar el mismo lugar con las mismas caracter�sticas. En mec�nica cu�ntica, la posici�n y la velocidad de una part�cula no pueden determinarse con una precisi�n absoluta.3 En consecuencia, dos electrones que se encuentren suficientemente cerca y posean la misma velocidad ser�an indistinguibles.
Sin embargo, el llamado principio de exclusi�n de Pauli proh�be que una situaci�n as� ocurra en la naturaleza: si dos electrones llegan a ocupar una misma posici�n, sus velocidades deben ser distintas, siendo la diferencia entre las velocidades necesariamente mayor que un cierto valor.4 Gracias al principio de exclusi�n, la materia no puede comprimirse arbitrariamente, porque los electrones de los �tomos lo impiden.
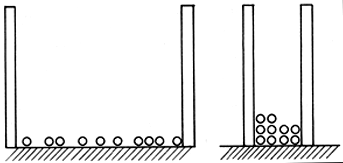
En el caso de una enana blanca, la materia est� tan comprimida que los n�cleos at�micos se "pegan" entre s�, formando una especie de red cristalina, y los electrones se mueven libremente a trav�s de esa configuraci�n de n�cleos, formando a su vez un "gas de electrones". Si la densidad de la materia es suficientemente alta, los electrones se enciman y, por el principio de exclusi�n, adquieren velocidades diferentes y cada vez m�s altas para poder ocupar un mismo volumen. La situaci�n es semejante a la de una caja llena con un n�mero fijo de canicas (figura 16); si la caja es suficientemente grande, las canicas se esparcen en su fondo; pero si se contraen las paredes de la caja, las canicas se amontonan unas encima de las otras, porque obedecen un "principio de exclusi�n": dos canicas no pueden estar en el mismo lugar y a la misma altura dentro de la caja. En el caso de las estrellas, el equivalente de la caja que se contrae es la estrella misma que reduce su tama�o, las canicas corresponden a los electrones y la altura sobre el fondo de la caja equivale a la velocidad de los electrones.
Los f�sicos llaman "electrones degenerados" a aquellos que adquieren su velocidad gracias al principio de exclusi�n de Pauli, por medio del mecanismo que hemos descrito. El punto fundamental es que un gas de electrones degenerados tiene propiedades muy distintas a las de la materia com�n. En particular, la presi�n y la densidad est�n relacionadas entre s� en forma distinta a la que ocurre en los gases normales.
En 1926, el astrof�sico ingl�s Ralph H. Fowler calcul� la configuraci�n de equilibrio de una estrella en la que la presi�n interna es producida por la degeneraci�n de los electrones, y no por el calor central como en las estrellas ordinarias. Fowler encontr� que la presi�n de los electrones degenerados siempre era suficiente para detener definitivamente la contracci�n gravitacional de las estrellas. El problema del estado �ltimo de las estrellas parec�a resuelto: todas terminan su evoluci�n como enanas blancas, brillando d�bilmente con lo poco que les queda de su calor inicial —como ceniza que se apaga lentamente—; al irse agotando ese �ltimo calor, la enana blanca se vuelve "enana roja" y finalmente "enana negra": un cuerpo totalmente apagado, comparable en tama�o a un planeta. Incidentalmente, estos no son los cuerpos oscuros de Laplace; un c�lculo simple muestra que la velocidad de escape de la superficie de una "enana negra" es de unos cuantos miles de kil�metros por segundo, cien veces inferior a la velocidad de la luz.
Tal era la situaci�n en 1930 cuando Subrahmanyan Chandrasekhar, en esa �poca un joven estudiante indio, se dio cuenta de que, en las condiciones de enanas blancas, los electrones degenerados alcanzan velocidades cercanas a la de la luz. Eso implicaba que hab�a que tomar en cuenta los efectos nuevos predichos por la teor�a de la relatividad y que ellos no hab�an sido considerados por los astrof�sicos hasta entonces. Chandrasekhar revis� los c�lculos de sus antecesores y encontr� una relaci�n entre la presi�n y la densidad de un gas de electrones degenerados distinta de la que Fowler hab�a usado. A partir de esa relaci�n resolvi� el problema del equilibrio de una enana blanca y encontr� un hecho sorprendente que no hab�a sido descubierto hasta entonces: la presi�n de los electrones degenerados s�lo puede detener el colapso gravitacional de la estrella si la masa de �sta es menor que un valor cr�tico —conocido ahora como l�mite de Chandrasekhar— que es de 1.5 veces la masa del Sol. Aquellas estrellas cuya masa excede este valor l�mite no pueden detener su colapso gravitacional y deben proseguir encogi�ndose. Con una visi�n prof�tica, el mismo Chandrasekhar concluy�: "... no es posible avanzar en la comprensi�n de la estructura estelar sin antes poder responder la siguiente pregunta fundamental: dado un conjunto confinado de electrones y n�cleos at�micos �qu� sucede si se comprime la materia indefinidamente?"
Empero, los resultados de Chandrasekhar fueron recibidos con gran escepticismo por la comunidad cient�fica. Los astrof�sicos no pod�an imaginarse qu� le sucede a una estrella que se sigue comprimiendo m�s all� del estado de enana blanca, por lo que prefer�an soslayar la pregunta planteada por Chandrasekhar y seguir pensando que la enana blanca es la etapa final de todas las estrellas. La actitud de Arthur Eddington, fundador de la astrof�sica y maestro de Chandrasekhar, es t�pica: a pesar de ser uno de los promotores m�s entusiastas de la teor�a de la relatividad, no pudo aceptar la idea de que los electrones degenerados pudieran alcanzar velocidades cercanas a la de la luz, por lo que invent� varios posibles mecanismos f�sicos que lo pudieran evitar. Eddington, como muchos de sus colegas, no conceb�a que una estrella se siguiera contrayendo despu�s de convertirse en una enana blanca: "... �creo que debe haber una ley de la naturaleza que impida que una estrella se comporte en forma tan absurda!" escribi� en 1935.
Pasaron m�s de dos d�cadas para que el trabajo de Chandrasekhar fuera aceptado plenamente por la comunidad cient�fica y cinco d�cadas para que se le concediera el premio Nobel. En la actualidad se conocen cientos de enanas blancas; algunas de ellas se encuentran en sistemas dobles, lo que ha permitido determinar sus masas: ninguna excede el l�mite de Chandrasekhar.
Seg�n las teor�as m�s recientes de la evoluci�n estelar, una estrella cuya masa no excede 6 u 8 veces la masa solar, arroja al espacio, en las �ltimas etapas de su evoluci�n, una gran parte de su materia principalmente cuando se expande y se vuelve una gigante roja. (En la figura 17, se ve la "nebulosa del anillo"; en realidad, el anillo es una cáscara de gas arrojado por la estrella central y calentado por �sta.) A la larga s�lo queda la parte central y m�s densa de la estrella, la cual se contrae hasta volverse una enana blanca.
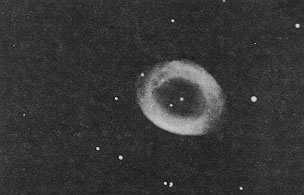
Figura 17. La Nebulosa de la Lira. El anillo es en realidad una c�scara esf�rica de gas iluminada por la estrella central.
Quedaba pendiente de responderse la pregunta planteada por Chandrasekhar: �qu� pasa con una configuraci�n de materia cuya masa excede la cr�tica? En el ejemplo anterior de la caja llena de canicas, la contracci�n de las paredes conducir�a, con el tiempo, a una situaci�n en la que las canicas, si no detienen la compresi�n, se rompen y se pulverizan. �Puede algo semejante suceder con los electrones?
Pocos meses despu�s de la publicaci�n del trabajo de Chandrasekhar, el gran f�sico sovi�tico Lev Landau propuso que, cuando la densidad de la materia excede la de una enana blanca, los electrones se ven forzados a fusionarse con los protones. Como resultado, predijo Landau, se llegar�a a una nueva configuraci�n de equilibrio, en la que la "densidad de la materia es tan alta que los n�cleos at�micos en contacto forman un solo y gigantesco n�cleo". S�lo unos meses despu�s, en el mismo a�o de 1932, James Chadwick descubri� el neutr�n, la part�cula sin carga el�ctrica que, junto con el prot�n, forma los n�cleos at�micos.
El problema de la evoluci�n estelar despu�s de la etapa de enana blanca se aclar� con la aparici�n del neutr�n. En una estrella cuya masa excede el l�mite de Chandrasekhar, los electrones degenerados no pueden detener la compresi�n y se ven forzados a fusionarse con los protones, formando neutrones. El resultado es una estrella de neutrones, un cuerpo de s�lo unas decenas de kil�metros de radio y tan denso como un n�cleo at�mico: una cucharada de la materia de estas estrellas pesa unos cien millones de toneladas.
El concepto de una estrella de neutrones apareci� por primera vez en 1934, en un art�culo de los astr�nomos Walter Baade y Fritz Zwicky sobre la naturaleza de las llamadas supernovas. Como rnencionamos anteriormente, las supernovas son cuerpos estelares que aparecen s�bitamente en el cielo, alcanzando un brillo muy superior al de cualquier estrella normal durante varias semanas, despu�s de lo cual se apagan paulatinamente.5 Una famosa supernova ocurri� en 1054 y fue registrada por los astr�nomos chinos, seg�n la cr�nica de La historia Sung. Las �ltimas que se observaron en nuestra propia galaxia tuvieron lugar en 1572 y en 1604; en ambos casos la estrella era tan brillante que se pod�a observar en pleno d�a.
A principios de 1987, apareci� una supernova en la Nube Mayor de Magallanes, una peque�a galaxia irregular, vecina de la V�a L�ctea., s�lo visible desde el Hemisferio Sur.6
Al estallar como supernova, una estrella llega a brillar como diez mil millones de estrellas juntas, tanto como todas las estrellas de una galaxia �De d�nde proviene tal cantidad de energ�a? Baade y Zwicky llegaron a la conclusi�n de que la estrella deber�a transformar una fracci�n sustancial de la materia central, en energ�a, seg�n la f�rmula de Einstein, E=mc�. Las capas m�s externas de la estrella son arrojadas violentamente al espacio interestelar y de la parte central �nicamente queda una estrella de neutrones.
Faltaba determinar si una estrella de neutrones pod�a mantenerse en equilibrio en contra de su propia fuerza gravitacional. Al igual que los electrones, los neutrones (y los protones) tambi�n obedecen al principio de exclusi�n de Pauli 7, por lo que, en una estrella de neutrones, se puede formar un gas de neutrones degenerados, cuya presi�n se opone a la fuerza gravitacional que tiende a contraer a la estrella.
En 1939, J. Robert Oppenheimer (mejor conocido por su contribuci�n a la fabricaci�n de la bomba at�mica) y George M. Volkoff estudiaron las posibles configuraciones de equilibrio de una estrella de neutrones, repitiendo lo que hab�a hecho unos a�os antes Chandrasekhar con las enanas blancas. La situaci�n era algo m�s complicada porque la atracci�n gravitacional en la superficie de una estrella de neutrones debe ser tan intensa que la velocidad de escape es cercana a la de la luz, por lo que la f�sica newtoniana deja de ser una buena aproximaci�n. Oppenheimer y Volkoff utilizaron, desde el principio, la teor�a de la relatividad general, combinada con la descripci�n f�sica de un gas de neutrones degenerados. El resultado que obtuvieron fue semejante al de Chandrasekhar: tambi�n para una estrella de neutrones existe un l�mite superior de masa, que result� un poco menor que la masa del Sol. Si la masa de la estrella es superior a ese l�mite, entonces la presi�n de los neutrones degenerados no puede detener el colapso gravitacional. Todo indicaba que las estrellas muy masivas terminan sus vidas en una forma "absurda", en contra de lo que pensaba Eddington.
Durante las tres d�cadas que siguieron a su presentaci�n en la sociedad cient�fica, la estrella de neutrones fue considerada un objeto fabuloso, producto de la mente de los te�ricos, pero sin confirmaci�n observacional. Sin embargo, la situaci�n cambi� dr�sticamente a finales de 1967. En aquellos d�as, Jocelyn Bell, una estudiante inglesa que preparaba su tesis doctoral sobre observaciones radioastron�micas, descubri� una se�al de radio en el cielo que pulsaba con una precisi�n asombrosa y con un periodo de apenas una fracci�n de segundo entre cada pulso. R�pidamente se encontraron otras fuentes de radio similares a las que se bautiz� con el nombre de pulsares.
Al principio, los astr�nomos propusieron diversas hip�tesis para explicar la naturaleza de los pulsares; inclusive se lleg� a pensar que se trataba de se�ales emitidas por seres inteligentes. Al a�o de su descubrimiento, todos se convencieron de que los pulsares eran �estrellas de neutrones!
Las estrellas, al igual que la Tierra, suelen poseer un campo magn�tico. Al contraerse la estrella, su campo magn�tico se "condensa" y aumenta su intensidad. En el caso de que se forme una estrella de neutrones, el campo magn�tico resultante llega a ser tan intenso que acelera los electrones a velocidades cercanas a la luminosa, y los hace radiar, principalmente en forma de ondas de radio.
Las estrellas tambi�n giran sobre s� mismas. Al contraerse, la velocidad de giro aumenta (�ste es un efecto f�sico utilizado, por ejemplo, por los patinadores: si empiezan a girar con los brazos abiertos, al cerrarlos aumentan su velocidad de rotaci�n). Es as� que una estrella, al contraerse, aumenta la velocidad con la que rota; si se vuelve estrella de neutrones, alcanza una velocidad de rotaci�n enorme, dando varias vueltas sobre s� misma por segundo.
Combinando el efecto de la radiaci�n producida por el intenso campo magn�tico con la rotaci�n de la estrella, se explica el origen de los pulsos observados por los radioastr�nomos. Un pulsar radia constantemente en una direcci�n definida por su campo magn�tico; esta direcci�n no coincide necesariamente con el eje de rotaci�n, as� que s�lo podemos recibir la se�al cuando el campo magn�tico apunta hacia nosotros (Figura 18, tal como un faro que, aparentemente, se prende y se apaga). As�, la frecuencia de los pulsos de un pulsar corresponde simplemente a su frecuencia de giro. Un pulsar debe necesariamente ser una estrella de neutrones, pues s�lo un cuerpo tan compacto y denso puede girar sobre s� mismo a la frecuencia de varias vueltas por segundo; una estrella com�n, o aun una enana blanca, se desbaratar�a inmediatamente al girar a esa enorme velocidad.
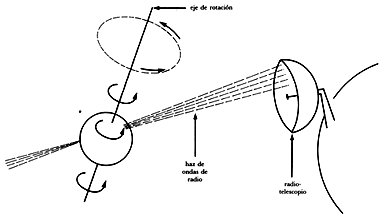
Figura 18. El efecto de faro. Un observador lejano ve un pulso de luz cada vez que el haz luminoso apunta hacia �l.
El descubrimiento de los pulsares reaviv� el estudio te�rico de las estrellas de neutrones. Los c�lculos originales de Oppenheimer y Volkoff se repitieron hace pocos a�os, tomando en cuenta las interacciones nucleares entre los neutrones. Los resultados m�s recientes indican que la m�xima masa de una estrella de neutrones debe ser aproximadamente de unas 2.5 veces la masa del Sol.
Seg�n las teor�as m�s aceptadas en la actualidad sobre la evoluci�n estelar, las estrellas con una masa superior a unas 6 u 8 masas solares terminan explotando como supernovas. Esta colosal explosi�n ocurre cuando los electrones degenerados en el centro de la estrella no logran detener el colapso gravitacional: en alg�n momento, el n�cleo estelar se comprime bruscamente y se produce una detonaci�n nuclear, en la que una fracci�n importante del centro de la estrella se transforma en energ�a, como una inmensa bomba at�mica, expulsando violentamente al espacio las capas externas de la estrella. En el lugar mismo de la explosi�n, s�lo queda un vestigio de lo que fue la estrella: la parte m�s central de su n�cleo, transformado en estrella de neutrones.
La famosa nebulosa del Cangrejo (Figura 19) es el remanente de la explosi�n de la supernova de 1054, descrita por los astr�nomos chinos. Baade y Zwicky conjeturaron que en el centro de esa nebulosa deber�a de encontrarse una estrella de neutrones, �nico resto no diseminado de la estrella que explot�. Y, efectivamente, en 1969 los radioastr�nomos descubrieron un pulsar justo en el centro de la nebulosa, confirmando as� la relaci�n entre remanente de supernova y estrella de neutrones.
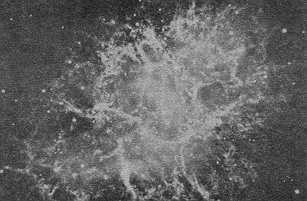
Figura 19. La nebulosa del Cangrejo, remanente de la explosi�n de una supernova.
Hoy en d�a se conocen m�s de 300 pulsares y sus caracter�sticas generales, deducidas de datos observacionales y modelos te�ricos, son las siguientes: su radio t�pico es de unos 10 km y la densidad alcanza, en el centro, un valor de cien millones de toneladas por cada cent�metro c�bico; estas estrellas poseen una corteza s�lida de aproximadamente un kil�metro de profundidad, por debajo de la cual el interior es l�quido con propiedades f�sicas muy particulares (en un estado que los f�sicos llaman super-fluido).
Ya que las estrellas de neutrones tampoco pueden exceder cierto l�mite de masa sin colapsarse, surge una vez m�s la pregunta �qu� pasa con aqu�llas demasiado masivas? Evidentemente seguir�n comprimi�ndose y sus neutrones, para no violar el principio de exclusi�n, tendr�n que fusionarse entre s� para transformarse en otros tipos de part�culas elementales, o, finalmente, romperse en sus constituyentes m�s b�sicos.
As� como los �tomos est�n constituidos por tres tipos de part�culas elementales (protones, neutrones y electrones), �stas, a su vez, no son tan elementales, seg�n las teor�as m�s recientes de la f�sica moderna. Existen evidencias recientes de que cada part�cula elemental "pesada", como el prot�n y el neutr�n, est� constituida, a su vez, por tres part�culas llamadas cuarks. La fuerza que amarra un cuark a otro es tan intensa que no puede existir un cuark aislado en la naturaleza.
Algunos f�sicos piensan que si una estrella de neutrones se sigue contrayendo, sus neutrones llegan a "romperse", de tal modo que se forma una estrella de cuarks. Los cuarks tambi�n satisfacen el principio de exclusi�n, por lo que se produce una presi�n de "cuarks degenerados" que podr�a, en principio, detener el colapso. Los c�lculos indican, sin embargo, que tambi�n para las estrellas de cuarks existe una masa cr�tica, de unas 6 masas solares, por encima de la cual la fuerza gravitacional vence a la presi�n y el colapso no se detiene. En este caso, los cuarks se fusionar�n entre s� para producir estados de la materia cada vez m�s ex�ticos y, por supuesto, m�s alejados de nuestra comprensi�n.
Hasta la fecha no se han encontrado evidencias observacionales de que las estrellas de cuarks existan, ni tampoco se entienden muy bien sus propiedades generales, pues este tipo de concepto se encuentra en los l�mites de los conocimientos actuales de la f�sica. Sin embargo, la historia de la astronom�a moderna nos ense�a que nunca se puede decir la �ltima palabra sobre las elucubraciones te�ricas de los astrof�sicos.
Hemos visto que ni los electrones ni los neutrones ni los cuarks degenerados pueden impedir el colapso gravitacional de una estrella suficientemente masiva. �Existe alg�n estado de la materia tal que su presi�n pueda resist�r a la fuerza gravitacional? Este problema se ha podido resolver en los �ltimos a�os y el resultado es bastante sorprendente. Se ha demostrado que, independientemente del mecanismo f�sico (conocido o a�n por conocer) que produce la presi�n, existe, necesariamente, una masa l�mite para que una configuraci�n esf�rica de materia permanezca en equilibrio sin colapsarse. La existencia de este l�mite de masa es una consecuencia directa de la teor�a de la relatividad general: no importa qu� tipo de presi�n se considere, la fuerza gravitacional vence definitamente cualquier fuerza de presi�n de la estrella si la masa de �sta supera unas 8 masas solares.
Existen teor�as de la gravitaci�n diferentes de la de Einstein, aunque ninguna tiene la misma simplicidad de conceptos y claridad te�rica. Se ha calculado la masa l�mite seg�n otras teor�as y excepto por algunas, muy ex�ticas y que no han sido confirmadas independientemente, se encuentra siempre que existe una masa l�mite, cuyo valor no discrepa demasiado del predicho por la relatividad general. Incluso para aquellos que dudan de la relatividad general u otras teor�as modernas, mencionemos que la teor�a cl�sica de Newton tambi�n predice un l�mite de masa, semejante a la relativista, para el equilibrio de una esfera masiva.
En conclusi�n, se puede afirmar que no existe en la naturaleza ning�n mecanismo f�sico que pueda oponerse a la fuerza gravitacional y detener el colapso de un cuerpo esf�rico con una masa superior a un cierto l�mite que, en ning�n caso, excede unas 8 masas solares (el valor preciso de ese l�mite depende del estado de la materia y de la teor�a gravitacional considerada). As�, cuando una estrella extremadamente masiva agota su combustible nuclear, empieza una contracci�n que produce, en alg�n momento, una explosi�n de supernova. El n�cleo de la estrella, que queda en el lugar de la explosi�n, seguir� su contracci�n si su masa supera a la cr�tica. Todav�a no hay unanimidad entre los astrof�sicos sobre cu�les ser�an las caracter�sticas del n�cleo remanente, pero es muy plausible que su masa exceda a la cr�tica, si la masa original de la estrella era muy grande. Este es un problema importante que est� siendo investigado en la actualidad. Se�alemos que existen estrellas cuyas dimensiones son unas 60 veces y posiblemente m�s,de las del Sol y, son �stas las que evolucionan m�s r�pidamente.
Finalmente, nos vemos enfrentados siempre al problema de una masa esf�rica que se comprime indefinidamente por su propia atracci�n gravitacional. Esta situaci�n fue estudiada en 1938 por el mismo Oppenheimer y otro colaborador suyo, Hartland Snyder, quienes llegaron a una conclusi�n extremadamente interesante utilizando la teor�a de la relatividad general. As�, estudiaron la evoluci�n de una esfera material sin ninguna presi�n interna que se contrae por su propia gravedad. La suposici�n de presi�n nula es una simplificaci�n v�lida en este problema particular; estudios m�s recientes, en los que se consideran cuerpos masivos m�s pr�ximos a los reales y dotados con presi�n interna, han confirmado que la forma cualitativa del colapso gravitacional no depende de la presi�n.
Seg�n la mec�nica newtoniana, una esfera masiva sin presi�n interna se contrae bajo su propia fuerza gravitacional, hasta que, en principio, toda la masa queda comprimida en un punto. Un resultado importante de la mec�nica cl�sica es que una esfera masiva atrae gravitacionalmente como si toda su masa estuviera concentrada en su centro, independientemente de su radio. En consecuencia, la atracci�n gravitacional de una esfera en contracci�n no var�a en un punto fijo del espacio; aumenta, eso s� la fuerza gravitacional en la superficie en movimiento de la esfera. As�, por ejemplo, si el Sol se comprimiera s�bitamente, sin alterar su masa, el efecto sobre el movimiento de los planetas ser�a nulo.
Algo similar ocurre seg�n la teor�a de la relatividad general. La atracci�n gravitacional de una esfera en la regi�n exterior a ella es del todo independiente de la contraci�n de la esfera; s�lo aumenta la intensidad de la gravedad en la superficie de la esfera a medida que se contrae, tal como en el caso newtoniano. Pero fen�menos extra�os suceden cuando la esfera se aproxima al radio de Schwarzschild que corresponde a su masa.
Consideremos, pues, una hipot�tica esfera masiva que se contrae. Oppenheimer y Snyder se dieron cuenta de que, de acuerdo con la teor�a de la relatividad, existen dos sistemas de referencia desde los cuales el colapso se ve de formas muy distintas: uno es el sistema de referencia de un observador en la superficie de la esfera y que se colapsa junto con ella; otro es el sistema de referencia de un observador externo que estudia el fen�meno desde un lugar lejano.
El observador situado en la superficie de la esfera ver� c�mo �sta se contrae progresivamente. El efecto f�sico m�s notable para �l ser� un aumento de la atracci�n gravitacional de la esfera: en efecto, la fuerza gravitacional en la superficie ir� aumentando en raz�n inversa al cuadrado del radio de la esfera (por la ley de Newton), lo que implica un aumento del peso del observador. Pero, aparte de ese molesto efecto, el observador no notar� nada particular, aun en el momento en que el radio de la esfera alcance el valor del radio de Schwarzschild (recordemos que este radio es igual a unos 3 km por cada masa solar de la esfera). Despu�s de cruzar el radio de Schwarzschild, seguir� el colapso de la esfera hasta que, en alg�n momento, la fuerza gravitacional ser� tan intensa que despedazar� al observador. Finalmente, toda la masa de la esfera se contraer� hasta comprimirse en un punto, de tama�o nulo, donde la fuerza gravitacional es infinita. A un punto as�, los f�sicos lo llaman singularidad; las leyes de la f�sica dejan de aplicarse en ese punto. Sin embargo, m�s que un concepto f�sico, la singularidad es un reconocimiento de nuestra ignorancia de las condiciones f�sicas extremas. Antes de que se forme una singularidad deben aparecer fen�menos cu�nticos que hasta ahora desconocemos y que, quiz� en el futuro, logremos entender si llegamos a una teor�a cu�ntica de la gravitaci�n.
Medido por el que acompa�a a la esfera en su contracci�n, el tiempo que transcurre entre el momento en que la esfera atraviesa su radio de Schwarzschild correspondiente y el momento en que se convierte en singularidad, depende fundamentalmente de la masa que posee la esfera; en t�rminos aproximados, es de unas cien mil�simas de segundo por cada masa solar de la esfera.
Supongamos ahora que el observador situado en la superficie de la esfera que se colapsa, env�a se�ales luminosas al espacio. Una vez que cruza el radio de Schwarzschild, estas se�ales no podr�n salir y acabar�n, con el tiempo, en la singularidad junto con la esfera masiva y el observador. Todo este proceso ser� visto de una manera muy distinta por un observador que haya quedado a una distancia prudente, quien ver� a la esfera acercarse a su radio de Schwarzschild correspondiente, pero sin llegar nunca a �l. Si el observador situado sobre la esfera posee un reloj y llega al radio de Schwarzschild a una cierta hora —las 3:00, por ejemplo— las manecillas de ese mismo reloj, vistas desde lejos, se acercar�n a esa hora cada vez m�s lentamente, sin nunca alcanzarla (Figura 20). Un observador lejano ver� todo el proceso del colapso como si �ste se hubiera filmado, y luego la pel�cula se proyectara cada vez m�s despacio, acerc�ndose sin llegar nunca al momento en que el reloj en la superficie marque las 3:00. As�, el proceso del colapso gravitacional hacia el radio de Schwarzschild ocurre en un tiempo finito para un observador que sigue el colapso, pero el mismo proceso parece tomar un tiempo infinito cuando es visto desde lejos: un caso extremo y muy ilustrativo de la relatividad del tiempo.
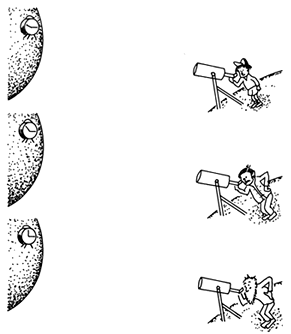
Figura 20. Un observador lejano ve el tiempo transcurrir cada vez m�s lentamente sobre la superficie de una esfera masiva que se acerca a su radio de Schwarzchild correspondiente.
El colapso gravitacional de una estrella suficientemente masiva debe acabar, seg�n todas las evidencias te�ricas, en la formaci�n de un hoyo negro. Para un cuerpo suficientemente lejano, la aparici�n de un hoyo negro no tendr� ninguna consecuencia f�sica novedosa, ya que, como vimos en las p�ginas anteriores la atracci�n gravitacional de una esfera s�lo depende de su masa y no de su radio. De hecho, un hoyo negro atrae, muy lejos de �l, exactamente como lo predice la ley de la gravitaci�n de Newton. Lo realmente novedoso, con respecto a la f�sica newtoniana, es lo que sucede cerca de la estrella que est� a punto de convertirse en hoyo negro. Vista desde afuera se ver� como una esfera que se acerca lentamente a su radio de Schwarzschild correspondiente, el tiempo transcurriendo cada vez m�s lentamente en su superficie, "congel�ndose" los procesos f�sicos que ocurren ah�. Por esta raz�n, algunos astrof�sicos propusieron, en un principio, llamar a estos cuerpos "estrellas congeladas"; pero el nombre de hoyo negro —inventado por el f�sico estadunidense John A. Wheeler— se volvi� m�s popular.
Hay que recordar que la m�trica de Schwarzschild describe el espacio-tiempo generado por un cuerpo masivo perfectamente sim�trico y que no gira. En una primera aproximaci�n, el espacio-tiempo alrededor de una estrella colapsada ser� el de Schwarzschild, aunque se podr�an esperar ciertas correcciones porque las estrellas no son perfectamente esf�ricas y, en particular, giran sobre s� mismas. Volveremos en el cap�tulo V al espacio-tiempo m�s general de un hoyo negro, pero antes veamos c�mo se pueden detectar los hoyos negros y confirmar su existencia.
NOTAS
1 En este libro utilizaremos siempre la escala Kelvin de temperatura. El cero de esta escala es el cero absoluto ( - 273.16�C ). Para pasar de grados Kelvin (�K) a grados cent�grados o Celsius (�C), hay que restar 273.16 grados.
2 V�ase El descubrimiento del Universo, S. Hacyan, n�m. 6 de La Ciencia desde M�xico, FCE.
3 M�s precisamente, si x es la incertidumbre en la posici�n y v la incertidumbre en la velocidad, entonces, para una part�cula de masa m, se tiene necesariamente x v > h/m, donde h es la constante de Planck; este es el principio de incertidumbre de Heisenberg volveremos a este principio en el capitulo VI.
4 Ese valor es h/(m.x); ver la nota anterior. Para no complicar la exposici�n, no consideramos la orientaci�n del esp�n de los electrones.
5 No hay que confundir las supernovas con las novas; estas últimas también son estrellas que aumentan su brillo súbitamente, pero no en la magnitud de una supernova. Los dos fenómenos se deben a mecanismos muy distintos.
6 En el momento de escribir estas l�neas, la supernova se encontraba en el m�ximo de su brillo y hab�a despertado un enorme inter�s entre los astr�nomos. Por primera vez se ofrece la oportunidad de estudiar una supernova relativamente cercana (170 000 a�os luz) con t�cnicas modernas.
7 Existen en la naturaleza dos tipos de part�culas: los fermiones, asosiados a la materia (electrones, protones, neutrones, etc.) y los bosones, asociados a las interacciones entre la materia (fotones, mesones, etc.) Todos los fermiones obedecen al principio de exclusi�n de Pauli.
