V. UN VIAJE POR LOS HOYOS NEGROS (Y BLANCOS)
PARA describir los fen�menos naturales, los f�sicos utilizan ecuaciones matem�ticas que representan las leyes de la naturaleza. Las soluciones de estas ecuaciones describen el comportamiento de los cuerpos materiales y sus interacciones mutuas, en condiciones espec�ficas. Sin embargo, la existencia de una soluci�n no es garant�a de que ocurra en la naturaleza el fen�meno que describe.
Consideremos por ejemplo, el caso de una canica en equilibrio sobre la punta de un alfiler. Las ecuaciones de la mec�nica cl�sica admiten una soluci�n que describe exactamente esa situaci�n; sin embargo, un an�lisis m�s completo de esas mismas ecuaciones revela lo que se conoce por experiencia: la soluci�n es matem�ticamente correcta pero inestable ya que cualquier perturbaci�n externa, por peque�a que sea, destruye el equilibrio de la canica. Por el contrario, si la canica se encuentra en el fondo de un agujero, una perturbaci�n externa no altera dr�sticamente su posici�n. En resumen, para que una soluci�n exacta de las ecuaciones de la mec�nica describa una situaci�n posible, debe ser, adem�s, una soluci�n estable.
En la teor�a de la relatividad general la curvatura del espacio-tiempo se calcula por medio de la ecuaci�n de Einstein, que relaciona esta curvatura con la cantidad de materia presente. Una clase de soluciones de esta ecuaci�n describe a los hoyos negros, la existencia de los cuales no est� asegurada a priori sino que debe confirmarse por medio de observaciones astron�micas.
La soluci�n de Schwarzschild no es la �nica soluci�n de la ecuaci�n de Einstein que corresponde a un hoyo negro. En el presente cap�tulo estudiaremos las clases de hoyos negros que, en principio, pueden existir y la curiosa estructura geom�trica del espacio-tiempo que generan.
EL ESPACIO-TIEMPO DE SCHWARZSCHILD: HOYOS NEGROS
Un espacio curvo se puede describir matem�ticamente, pero es imposible de visualizar o dibujar, a menos de que el n�mero de dimensiones sea dos. Para tener una imagen pict�rica del espacio-tiempo curvo, conviene considerar s�lo una secci�n bidimensional de �l. Una manera de lograr esto es representar s�lo aquellos sucesos que ocurren en un momento dado y en cierto plano espacial.
Empecemos con el espacio-tiempo de Minkowski. Definimos el plano de simultaneidad como el conjunto de sucesos que ocurren en alg�n plano espacial a un mismo tiempo; este tiempo depende, por supuesto, del observador que lo mide, por lo que distintos observadores definir�n planos de simultaneidad diferentes. Por ejemplo, el conjunto de sucesos que ocurren sobre la superficie de una mesa a las 3 P.M. hora de Greenwich, es un plano de simultaneidad (Figura 30). La ventaja de esta construcci�n es que el plano de simultaneidad es una superficie de dos dimensiones, que podemos visualizar y dibujar. Hay que notar, sin embargo, que este plano no puede observarse directamente porque la luz tarda un cierto tiempo en ir de un punto a otro. Un observador que se encuentra sobre la mesa del ejemplo anterior ver� �nicamente el punto-suceso donde �l se encuentra a las 3 P.M.; un segundo despu�s ver� los sucesos que ocurrieron a las 3 P.M. a 300 000 km de distancia de �l sobre la superficie de simultaneidad; dos segundos despu�s ver� aquellos que ocurrieron a 600 000 km; y as� sucesivamente; mientras m�s espera, m�s puntos-sucesos del plano podr� observar (pero �l ya no estar� en el plano de simultaneidad, aunque s� en la mesa, porque su reloj ya no marca las 3 P.M.).
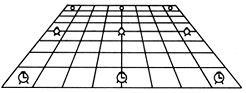
Figura 30. Un plano de simultaneidad. Cada punto del plano es un suceso que ocurre a la misma hora (las 3 P.M., por ejemplo).
Supongamos ahora que colocamos una esfera masiva en el espacio-tiempo. Afuera de la esfera, el espacio-tiempo es el de Schwarzschild y dentro de ella es de alguna otra forma (que no nos interesa por ahora para nuestros fines). El plano de simultaneidad se vuelve una superficie de simultaneidad deformada, tal como se muestra en la figura 31.
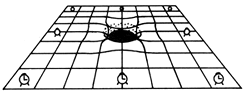
Figura 31. Un cuerpo masivo deforma el plano de simultaneidad.
Si la esfera se contrae, la forma de la superficie de simultaneidad correspondiente a tiempos distintos no es la misma. Un observador lejano ver� a la esfera contraerse y acercarse, sin nunca alcanzar su radio de Schwarzschild correspondiente; en consecuencia, la superficie de simultaneidad correspondiente al tiempo del observador externo tendr� una forma que depende del tiempo considerado, tal como se muestra en la figura 32. Hay que notar, adem�s, que lejos de la esfera masiva, la superficie de simultaneidad es plana; esto es consecuencia de que la atracci�n gravitacional de la esfera disminuye con la distancia, por lo que lejos de ella, el espacio-tiempo se vuelve plano.
Figura 32. A medida que un cuerpo masivo se comprime, aumenta la deformaci�n de la superficie de simultaneidad.
Como vimos anteriormente, el colapso de una esfera masiva tiene una apariencia muy distinta para un observador montado en ella; tal observador cruza el radio de Schwarzschild, penetra al hoyo negro —cuya formaci�n presencia— prosigue su viaje con la esfera hasta llegar a la singularidad en el centro del hoyo negro, donde termina su existencia.
Si construimos las superficies de simultaneidad asociadas al tiempo del observador que penetra al hoyo negro, tendremos una sucesi�n como la mostrada en la figura 33. En este caso, aparece el interior del hoyo negro y, finalmente, surge la singularidad cuando la esfera masiva se concentra toda en un punto. En alg�n momento, el observador que penetr� al hoyo negro choca con la singularidad y termina definitivamente su viaje.
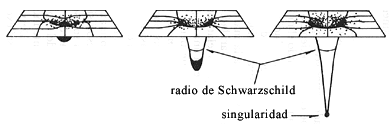
Figura 33. La superficie de simultaneidad alrededor de una esfera masiva que se comprime hasta quedar dentro de su radio de Schwarzschild y volverse una singularidad. El tiempo simult�neo en cada figura es el de un observador que acompa�a a la esfera en su contracci�n.
EL ESPACIO-TIEMPO DE SCHWARZSCHILD: HOYOS ETERNOS Y HOYOS BLANCOS
Hemos se�alado varias veces que la soluci�n de Schwarzschild describe el espacio-tiempo en la regi�n alrededor de una esfera masiva, siendo el radio de dicha esfera completamente arbitrario. La soluci�n matem�tica encontrada por Schwarzschild es v�lida aun si se supone que el radio de la esfera masiva ha sido cero en todo tiempo o, en otras palabras, si toda la masa ha estado concentrada eternamente en una singularidad. En este caso, la estructura del espacio-tiempo es relativamente simple: un horizonte dentro del cual est� una singularidad y fuera de �l, a lo lejos, el espacio que tiende a ser plano. Hay que precisar que un objeto as�, no es el que se forma por el colapso de un cuerpo masivo; por el contrario, tiene que haber existido desde un pasado infinito y seguir existiendo tal cual durante una eternidad. Por esta raz�n, es m�s apropiado llamarlo un hoyo eterno. A diferencia de los hoyos negros que se forman por el colapso de la materia, lo cual es un proceso f�sico perfectamente comprensible, los hoyos eternos son soluciones matem�ticas de las ecuaci�n de Einstein cuya realidad es discutible. Sin embargo, la estructura del espacio-tiempo asociada a un hoyo eterno es sumamente interesante y vale la pena estudiarla con cierto detalle. Despu�s de todo, la existencia de los hoyos eternos no est� excluida a priori y podr�a representar, en una primera aproximaci�n, alguna propiedad misteriosa del espacio-tiempo.
Consideremos para empezar, la superficie de simultaneidad asociada al tiempo de un observador lejano del hoyo eterno. A diferencia del hoyo negro, no hay una regi�n correspondiente al interior de una esfera masiva, como en la figura 32, sino que la superficie de simultaneidad toma la forma que se muestra en la figura 34.
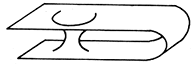
Figura 34. La superficie de simultaneidad de un hoyo eterno. Aqu� aparecen dos regiones sim�tricas, unidas entre s� por el puente de Einstein-Rosen. El tiempo de simultaneidad es el de un observador lejano.
Lo m�s notable de esta estructura es que el espacio-tiempo posee dos regiones que se vuelven planas a lo lejos, de modo tal que aparecen dos universos conectados entre s� a trav�s del hoyo eterno. Esta extra�a estructura del espacio-tiempo fue descubierta por Einstein y su colaborador Nathan Rosen en los a�os veinte y ha generado un gran n�mero de especulaciones. Se ha sugerido que podr�an existir universos paralelos que se conectar�an entre s� a trav�s del llamado puente de Einstein-Rosen. M�s a�n, John A. Wheeler ha sugerido que los dos universos paralelos podr�an ser, en realidad, uno solo (tal como se muestra en la figura 35), en cuyo caso el puente de Einstein-Rosen unir�a dos regiones lejanas del espacio: m�s que un puente se tendr�a lo que Wheeler llam� un hoyo de gusano.
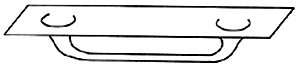
Figura 35. Es posible identificar entre s� las dos regiones de cada lado del puente. El resultado es un "hoyo de gusano".
�Se puede viajar a trav�s del puente de Einstein-Rosen, o al menos, ver a trav�s de �l y atisbar ese hipot�tico universo paralelo? �La respuesta es negativa! No hay que olvidar que la superficie de simultaneidad no es directamente observable. M�s bien, debemos plantearnos la pregunta: �c�mo se ve un hoyo eterno? cuya contestaci�n contiene nuevas sorpresas.
Un an�lisis detallado del espacio-tiempo de un hoyo eterno muestra que la singularidad es en realidad doble. Existe una singularidad en el pasado y una singularidad en el futuro. Entre las dos, hay un breve momento en el que deja de existir cualquier singularidad; la superficie de simultaneidad correspondiente a ese momento es la que contiene el puente de Einstein-Rosen (es por esta raz�n que no aparece la singularidad en la figura 34).
Un observador lejano s�lo puede ver la singularidad pasada de un hoyo eterno, porque s�lo se puede observar el pasado. Esta singularidad se ver� rodeada de un horizonte que deja pasar la materia y la luz en un solo sentido, pero, a diferencia del hoyo negro, este sentido es de �adentro hacia afuera! Todo lo que originalmente se encuentra dentro del horizonte es expelido hacia el exterior: un hoyo eterno tiene la apariencia de un hoyo negro al rev�s, o lo que se ha bautizado hoyo blanco.
El hecho de que la luz sale de un hoyo blanco permite ver su singularidad en el pasado, ya que se puede observar el pasado. Por otra parte, un hoyo blanco arroja hacia el exterior todo lo que se encuentra dentro de su horizonte, aunque atrae gravitacionalmente todo cuerpo fuera de su horizonte, tal como lo hace cualquier cuerpo masivo. Cualquier cuerpo dentro del horizonte del hoyo blanco tuvo que surgir necesariamente de la singularidad en el pasado; esto es exactamente lo contrario de un hoyo negro: cualquier cuerpo que est� dentro de su horizonte termina cayendo a la singularidad en el futuro.
Consideremos ahora un observador que decide viajar hacia el hoyo eterno. Si inicialmente se encuentra fuera del horizonte, entonces puede cruzar el horizonte de afuera hacia adentro, tal como si se tratara de un hoyo negro. Esto no es contradictorio con el hecho de que un hoyo blanco expele su contenido. Lo que sucede es que un hoyo eterno posee, en el mismo lugar, un horizonte pasado —el del hoyo blanco— y un horizonte futuro —el del hoyo negro—. Dado que el tiempo fluye en un solo sentido, se observa el pasado y se "viaja" hacia el futuro. Un hoyo eterno es blanco en el pasado y negro en el futuro.
Para aclarar lo anterior, sigamos con nuestro observador que se deja caer al hoyo eterno. �l ver� que se acerca a un hoyo blanco cuya singularidad es visible y de la que fluye todo lo que se encuentra dentro del horizonte. En alg�n momento llegar� al horizonte y penetrar� a lo que, en el futuro, actuar� para �l como un hoyo negro. En el instante en que cruza el horizonte tendr� una visi�n s�lo reservada a los que se atreven a penetrar un hoyo eterno: a partir de ese momento podr� observar el universo paralelo, cuya luz recibir� a trav�s del puente de Einstein-Rosen. Desgraciadamente no podr� comunicar sus impresiones a su universo de origen; el observador se encuentra en un hoyo negro del que no puede salir ninguna se�al que emita. Su destino inexorable es la singularidad futura. Despu�s de un breve momento en que observar� dos universos simult�neamente, terminar� su viaje en la singularidad del hoyo negro.
Todo intento de pasar de un universo a otro (o de una regi�n de nuestro universo a otra regi�n) a trav�s del puente de Einstein-Rosen (o de un hoyo de gusano) est� condenado al fracaso. S�lo una part�cula que viaje m�s r�pido que la luz lograr�a penetrar al hoyo eterno, evitar la singularidad y salir en el otro universo. Sin embargo, como hemos se�alado anteriormente, la f�sica actual excluye toda posibilidad de viajar a mayor velocidad que la luz.
A pesar de ser, hasta ahora, s�lo soluciones matem�ticas, los hoyos blancos no dejan de tener cierto encanto.
Algunos astr�nomos han sugerido que los misteriosos cuasares son hoyos blancos funcionando como fuentes c�smicas de materia. Quiz�s nuestro universo est� lleno de hoyos blancos y las galaxias se han generado a partir de �stos. Estas especulaciones son muy atractivas, pero existen algunos problemas serios relacionados con el concepto de un hoyo blanco que hacen dudar de su realidad.
Toda la materia que se encuentra en un hoyo blanco tuvo necesariamente que surgir de la singularidad ah� presente. �Cu�l es el destino de esa materia al cruzar el horizonte y salir a nuestro universo? Para simplificar la discusi�n, imaginemos un observador (obviamente no terrestre) que haya nacido dentro del hoyo blanco. Antes de llegar al horizonte no puede ver ninguno de los universos paralelos en el exterior; la luz que recibe se origin� tambi�n en la singularidad, por lo que s�lo puede observar esa singularidad. En alg�n momento, nuestro hipot�tico observador llega al horizonte y se adentra en nuestro propio universo (o al paralelo); a partir de ese instante puede ver lo que sucede fuera de su hoyo blanco ... pero en una forma muy especial. Recordemos que si un observador cae a un hoyo negro, el tiempo que tarda en llegar al horizonte es finito para �l, pero ese mismo tiempo es infinito para un observador lejano que lo ve penetrar al hoyo. En el caso de un hoyo blanco, se tiene una situaci�n contraria: lo que es un intervalo de tiempo finito para el observador que emerge del hoyo blanco es un intervalo infinito para un observador lejano. En este caso, es el que sale del hoyo quien ve a lo lejos lo que ocurri� en el pasado. Al asomarse del horizonte, nuestro hipot�tico observador presencia, en lo que es un instante para �l, el pasado infinitamente remoto de nuestro propio universo.
Empero esta visi�n de la eternidad pasada tiene un muy alto costo. Debido a la contracci�n infinita del tiempo de los procesos externos, cualquier radiaci�n emitida en el exterior es recibida con una energ�a infinita por quien emerge del hoyo blanco. Como consecuencia toda materia que intente salir de un hoyo blanco es inmediatamente desintegrada y las part�culas que la constitu�an quedan "embarradas" eternamente en el horizonte. Se forma as� una especie de c�scara material que envuelve al hoyo blanco y �ste se vuelve, para todo fin pr�ctico, un hoyo negro.
Este fen�meno ha hecho dudar seriamente de la existencia de los hoyos blancos o eternos. La implicaci�n de fondo es que, a diferencia de los hoyos negros, tales construcciones te�ricas son soluciones inestables de las ecuaciones de Einstein, en el mismo sentido que una canica en equilibrio sobre la punta de un alfiler representa una soluci�n inestable de las ecuaciones de la mec�nica cl�sica.
Por otra parte, hay que aclarar que el an�lisis que hemos esbozado se refiere al caso idealizado de un hoyo eterno en un universo vac�o e infinito tanto en extensi�n como en duraci�n. Por supuesto, esto es s�lo una aproximaci�n al universo real, pero las propiedades cualitativas de un hoyo eterno en un universo m�s realista no cambian dr�sticamente... aunque, en f�sica te�rica, no siempre se puede decir la �ltima palabra.
ESPACIO-TIEMPO DE REISSNER-NORDSTROM: HOYOS NEGROS CARGADOS
Apenas unos meses despu�s de que Schwarzschild descubri� la soluci�n que lleva su nombre, los f�sicos H. Reissner y G. Nordstrom encontraron, en forma independiente, otra soluci�n de las ecuaciones de Einstein que representa el espacio-tiempo afuera de una esfera que, adem�s de masa, posee una carga el�ctrica.
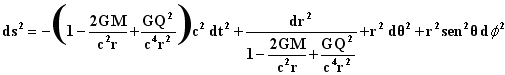
La soluci�n de Reissner-Nordstrom (Figura 36) generaliza la de Schwarzschild. Posee dos par�metros, la masa M y la carga Q de la esfera que deforma al espacio-tiempo1. En el caso particular en que la carga es cero, la soluci�n se reduce a la de Schwarzschild con masa M.
Al igual que el espacio-tiempo de Schwarzschild, el de Reissner-Nordstrom posee un horizonte que s�lo puede ser cruzado en un sentido; es, por lo tanto, un hoyo negro el�ctricamente cargado.
En principio, tal hoyo negro podr�a formarse por el colapso gravitacional de una esfera masiva el�ctricamente cargada. El proceso es esencialmente como en el caso sin carga: visto desde lejos, el tiempo sobre la superficie de la esfera parece congelarse a medida que la superficie de �sta se acerca al horizonte, mientras que un observador montado en la esfera cruza el horizonte en un tiempo finito.
Sin embargo, las estrellas no tienen carga el�ctrica, como casi todos los cuerpos macrosc�picos en estado natural que poseen tantos electrones negativos como protones positivos. Por esta raz�n, no es factible que, en una situaci�n real, se forme un hoyo negro cargado a consecuencia del colapso gravitacional de una estrella. Una manera m�s simple de cargar el�ctricamente a un hoyo negro es inyectarle cargas el�ctricas despu�s de que se haya formado. Si, por ejemplo, un hoyo negro sin carga atrapa un haz de electrones que atraviesa el espacio, adquiere la carga de esos electrones; el espacio-tiempo alrededor de ese hoyo negro ser�, entonces, el de Reissner-Nordstrom.
La principal peculiaridad de un hoyo negro cargado es que, a diferencia de uno neutro, posee dos horizontes conc�ntricos, centrados alrededor de la singularidad (Figura 37).
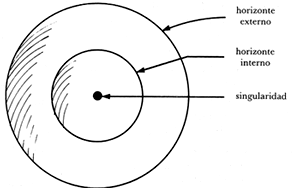
Los radios de los horizontes externos e internos, que denotaremos r+
y r- respectivamente, son
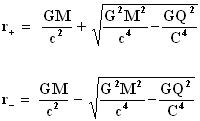
Por supuesto, un observador externo s�lo puede ver lo que sucede afuera del horizonte externo.
Si la carga Q del hoyo es igual a su masa M multiplicada por raíz cuadrada de G (es decir Q = raíz cuadrada de G M) los dos horizontes se funden en uno solo. Si la carga Q es mayor que raíz cuadrada de GM, simplemente no hay horizonte; en este caso no existe un hoyo negro sino una singularidad desnuda.
A partir de las consideraciones anteriores, se podr�a pensar que una manera
de destruir el horizonte de un hoyo negro y "liberar" su interior, es arrojar
part�culas cargadas al hoyo hasta que su carga llegue a ser lo suficientemente
grande como para que desaparezcan los horizontes. Sin embargo, las part�culas
cargadas que penetran a un hoyo negro poseen energ�a el�ctrica; como la energ�a
es equivalente a la masa, no s�lo aumenta la carga del hoyo negro sino tambi�n
su masa y, la carga Q nunca alcanza el valor cr�tico
M. Como veremos en el cap�tulo siguiente, no es posible destruir
el horizonte de un hoyo negro "manipul�ndolo" desde afuera. (Como dato curioso,
la carga de un electr�n es unas 1020 veces mayor que su masa multiplicada
por , por lo que un electr�n
no puede parecerse en nada a un hoyo negro.)
Al igual que la m�trica de Schwarzschild, la de Reissner-Nordstrom describe el espacio-tiempo en el exterior de una esfera de radio arbitrario. Nada impide reducir matem�ticamente ese radio a cero y estudiar as�, el espacio-tiempo de una masa y una carga concentradas en un punto. Como en el caso sin carga, se obtiene de este modo una soluci�n de las ecuaciones de Einstein que describe un hoyo eterno con carga el�ctrica. Sin embargo, la presencia de dos horizontes cambia radicalmente la estructura del espacio-tiempo en la vecindad del hoyo.
El primer hecho notable es que el espacio-tiempo de Reissner-Nordstrom posee una infinidad de universos paralelos en lugar de los dos que posee el espacio-tiempo de Schwarzschild. Pero a�n m�s interesante, es el hecho de que, en el caso de un hoyo eterno cargado, s� es posible pasar de un universo a otro sin toparse con la singularidad. El secreto es penetrar a la regi�n dentro del horizonte interno antes de intentar salir. A diferencia del caso de Schwarzschild, es posible moverse dentro del horizonte interno sin caer a la singularidad (de hecho, en esa regi�n, la singularidad no atrae sino repele gravitacionalmente). As�, una nave espacial puede penetrar a un hoyo eterno cargado cruzando su horizonte externo, meterse a la regi�n dentro del horizonte interno y, una vez ah�, teniendo cuidado de no toparse con la singularidad, salir, cruzando primero el horizonte interno y luego el externo (Figura 38). Seg�n este itinerario, los tripulantes de la nave habr�n penetrado a un hoyo negro en nuestro universo para salir de un hoyo blanco en otro universo.
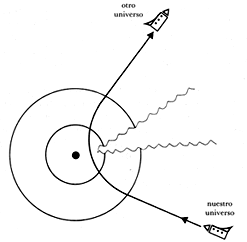
Sin embargo, un viaje entre universos conlleva peligros mortales. Se ha demostrado que el acercarse al horizonte interno del hoyo produce un efecto semejante al que ocurre cuando se emerge de un hoyo blanco. Una nave espacial que penetre a un hoyo cargado seguir� observando el universo exterior, aunque ya no pueda comunicarse con �l. A medida que la nave se acerca al horizonte interno, los tripulantes ver�n el tiempo en el exterior pasar cada vez m�s y m�s r�pidamente, como si estuvieran viendo a todo el Universo filmado en c�mara r�pida. En el momento de llegar al horizonte interno habr�n presenciado, en lo que es un instante para ellos, toda la historia futura del universo hasta tiempos infinitos. Desgraciadamente, esta misma visi�n de la eternidad futura implica la destrucci�n del observador. Toda la radiaci�n emitida en el exterior es recibida por la nave con una energ�a cada vez mayor a medida que se acerca al horizonte interno: para los tripulantes, el brillo de las estrellas aumenta sin l�mite y, finalmente, destruye cualquier cuerpo material que se acerque al horizonte interno.
As�, tampoco parece factible viajar a trav�s de un hoyo cargado. Una vez m�s, tenemos una soluci�n matem�ticamente v�lida pero inestable.
EL ESPACIO-TIEMPO DE KERR. HOYOS NEGROS ROTANTES
La Tierra, el Sol, las estrellas y pr�cticamente todos los cuerpos en el Universo giran sobre s� mismos. En mec�nica, el movimiento de rotaci�n de un cuerpo se mide por medio del momento angular, que es esencialmente el producto de tres factores: la masa, el radio y la velocidad de rotaci�n del cuerpo considerado (la relaci�n exacta depende de la distribuci�n de masa del cuerpo). Una de las leyes fundamentales de la mec�nica es que el momento angular de un cuerpo se conserva —en ausencia de cierto tipo de fuerzas externas, como la fricci�n con un medio externo o las fuerzas de marea—. Gracias a esta ley de conservaci�n, la Tierra gira sobre s� misma en un d�a y alrededor del Sol en un a�o, sin que estos lapsos hayan variado, apreciablemente, durante millones de a�os. La misma conservaci�n del momento angular implica que si un cuerpo rotante disminuye su tama�o, debe aumentar su velocidad de rotaci�n en proporci�n inversa, ya que el producto (masa) X (radio) X (velocidad de rotaci�n) permanece constante.
Debido a la conservaci�n del momento angular, una estrella que se contrae aumenta la velocidad con la que gira (un buen ejemplo es una estrella de neutrones; ver cap�tulo III). Asimismo, un hoyo negro que se forma por el colapso gravitacional de una estrella debe preservar el momento angular inicial del astro.
Antes de seguir, aclaremos una cuesti�n importante: �acaso se puede medir el momento angular de un hoyo negro? En contra de lo que podr�a esperarse, tal medici�n es posible, aunque de manera indirecta. La relatividad general predice un curioso efecto —descubierto por J. Lense y Hans Thirring en 1918— por el cual un cuerpo masivo en rotaci�n no s�lo atrae gravitacionalmente a otros cuerpos masivos en su vecindad sino que tambi�n los arrastra en el sentido de su rotaci�n (Figura 39). As� como un objeto al girar en el agua, forma un remolino que arrastra consigo a las part�culas del ruedo, an�logamente, el efecto de Lense-Thirring hace que el espacio-tiempo alrededor de un cuerpo rotante arrastre la materia a su alrededor.
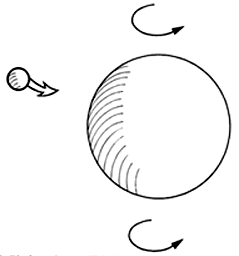
Figura 39. El efecto Lense-Thirring: un cuerpo masivo en rotaci�n arrastra a otro.
Este efecto es pr�cticamente imperceptible si la velocidad de rotaci�n del cuerpo masivo es mucho menor que la velocidad de la luz, raz�n por la cual no se puede detectar en experimentos terrestres. Sin embargo, permite medir, al menos en principio, el momento angular de un hoyo negro observando la trayectoria de una part�cula de prueba a su alrededor.
Con esta aclaraci�n, regresemos a los hoyos negros con momento angular. Tanto la soluci�n de Schwarzschild como la de Reissner-Nordstrom describen un espacio-tiempo con una perfecta simetr�a esf�rica. �ste, evidentemente, no puede ser el espacio-tiempo de un hoyo negro rotante, ya que la rotaci�n define una direcci�n particular —el eje de rotaci�n— que rompe la simetr�a esf�rica.
Es realmente notable que haya pasado casi medio siglo despu�s de la muerte de Schwarzschild para que se encontrara otra soluci�n de las ecuaciones de Einstein que describa el espacio-tiempo de un cuerpo en rotaci�n. Esta soluci�n fue descubierta en 1964 por el campe�n de bridge neozeland�s Roy P. Kerr, cuando preparaba su tesis doctoral de f�sica en la Universidad de Texas.
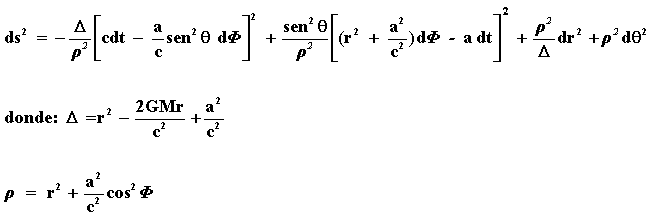
La soluci�n de Kerr describe el espacio-tiempo de un hoyo negro rotante. Como tal, posee dos par�metros: la masa M y el momento angular S del hoyo. En el caso particular en que S es cero, la soluci�n de Kerr se reduce exactamente a la de Schwarzschild. En la figura 40 se muestra la forma expl�cita de la soluci�n;2 el lector notar� que es considerablemente m�s complicada que la de Schwarzschild.
Cualquier esfera masiva genera en su exterior un espacio-tiempo de Schwarzschild, pero no cualquier cuerpo rotante produce un espacio-tiempo de Kerr. Durante varios a�os, los f�sicos y matem�ticos trataron infructuosamente de encontrar una configuraci�n de materia que pudiera originar el espacio-tiempo de Kerr; finalmente, se convencieron de que esta soluci�n de las ecuaciones de Einstein s�lo puede corresponder a un hoyo negro. Volveremos a este punto en el pr�ximo cap�tulo.
La estructura espacio-temporal de un hoyo negro rotante es similar, en varios aspectos, a la de un hoyo negro cargado. Como este �ltimo, tambi�n posee dos horizontes conc�ntricos, si el momento angular entre la masa, a, no excede del valor GM/c. El radio de cada horizonte, r + y r - est� dado por las f�rmulas
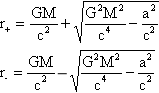
La singularidad se encuentra dentro del horizonte interno, pero, a diferencia del caso sin rotaci�n, la singularidad del espacio-tiempo de Kerr no es un punto sino un anillo (Figura 41).
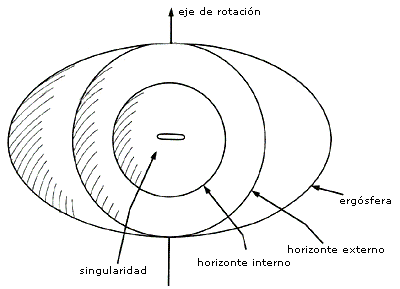
Si el par�metro de momento angular a es igual al valor cr�tico GM/c, los dos horizontes se fusionan en uno solo. Si a es mayor que GM/c, no hay horizontes: la singularidad queda desnuda y se puede observar desde una distancia prudente. Sin embargo, como veremos m�s adelante, es imposible destruir el horizonte de un hoyo negro arroj�ndole part�culas para hacerlo girar m�s r�pidamente y aumentar de este modo, su momento angular.
Al igual que el espacio-tiempo de Reissner-Nordstrom, el de Kerr posee una infinidad de universos y es posible viajar de uno a otro utilizando el itinerario que hemos descrito anteriormente: una nave espacial que penetre al hoyo negro puede llegar a la regi�n dentro del horizonte interno, evitar la singularidad y salir de un hoyo blanco en otro universo. Otra posibilidad es meterse por en medio del anillo de la singularidad, en cuyo caso la nave exploradora penetrar� en un extra�o universo donde el tiempo fluye tanto hacia el futuro como tambi�n hacia el pasado.
El lector probablemente a estas alturas, habr� adivinado que el viaje descrito es imposible por la misma raz�n que se�alamos en el caso de un hoyo cargado. Al acercarse al horizonte interno del espacio-tiempo de Kerr, los tripulantes ver�n el tiempo, en el exterior, fluir cada vez m�s r�pido y, a la vez, la radiaci�n proveniente del exterior aumentar indefinidamente de intensidad. La nave espacial ser�a destruida en su totalidad, antes de llegar al horizonte interno.
Una de las peculiaridades m�s interesantes de un hoyo negro rotante es la existencia de una zona llamada erg�sfera,3 situada precisamente afuera del horizonte interno, en donde ning�n cuerpo puede mantenerse inm�vil, por mucha energ�a que invierta para aferrarse a una misma posici�n. La causa de este fen�meno es el efecto de Lense-Thirring llevado al extremo: el arrastre producido por la rotaci�n del hoyo negro es tan intenso cerca del horizonte que todos los cuerpos sin excepci�n se ven forzados a girar junto con �l.
Dado que la erg�sfera se encuentra fuera del horizonte externo, es posible que una part�cula al penetrar esa regi�n pueda salir de ella y se aleje del hoyo. Esta posibilidad sugiri� a Roger Penrose un curioso mecanismo para extraer energ�a de un hoyo negro rotante. Supongamos que una part�cula masiva es arrojada al hoyo negro y que, estando en la erg�sfera, se rompe en dos pedazos, de tal forma que un pedazo penetra al hoyo y el otro se escapa (Figura 42). Penrose demostr� que, para algunas trayectorias, es posible que el pedazo que se escapa salga con m�s energ�a de la que pose�a la part�cula entera antes de entrar. As�, en principio, ser�a posible utilizar un hoyo negro rotante como fuente de energ�a; se mandan part�culas a la erg�sfera con una trayectoria bien calculada y se recogen los pedazos de esas part�culas, arrojados con una energ�a mayor que la original.
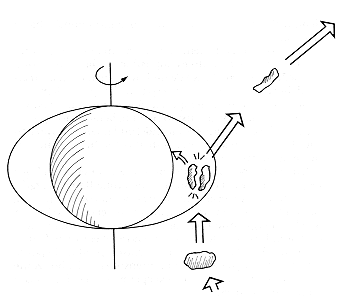
Figura 42. El mecanismo de Penrose para extraer energ�a de un hoyo negro rotante.
Lo que sucede en el efecto Penrose es que el hoyo negro cede parte de su energ�a a costa de reducir su momento angular. La "explotaci�n" de un hoyo negro puede durar, en principio, hasta que �ste agote su momento angular y se reduzca a un hoyo negro de Schwarzschild.
Se ha especulado mucho sobre el efecto Penrose: �es s�lo una curiosidad te�rica o, por el contrario, puede ser un mecanismo utilizado por la naturaleza para generar energ�a en el Universo? Un hoyo negro que se encuentre rodeado de materia podr�a arrojar parte de �sta a lo lejos por el mecanismo descrito. Hasta ahora, los c�lculos te�ricos no son concluyentes: las condiciones para que se d� el efecto Penrose son demasiado restrictivas para que sea un mecanismo eficiente (sin embargo, tambi�n se ha demostrado que esa eficiencia puede aumentar considerablemente si existe un campo magn�tico cercano).
EL ESPACIO-TIEMPO DE KERR-NEWMAN. HOYOS NEGROS ROTANTES Y CARGADOS
As� como la soluci�n de Schwarzschild se puede extender al caso con carga el�ctrica, tambi�n se puede generalizar la soluci�n de Kerr para describir un hoyo negro que, adem�s de rotar, posee carga. Tal soluci�n fue obtenida por E. T. Newman y sus colaboradores dos a�os despu�s del descubrimiento de Kerr.
El espacio-tiempo de Kerr-Newman est� determinado por tres par�metros: la masa M, el momento angular S y la carga Q. La forma de la soluci�n es parecida a la de Kerr y se muestra en la figura 43 (donde a =S/M). Si la carga Q se hace cero, la soluci�n se reduce a la de Kerr. Si el momento angular S se anula, la soluci�n se reduce a la de Reissner-Nordstrom, como se podr�a esperar.
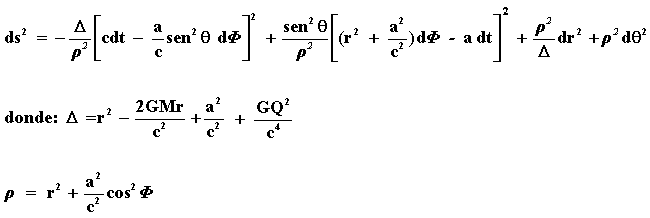
El espacio-tiempo de Kerr-Newman posee dos horizontes conc�ntricos, cuyos radios r+ y r- son
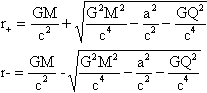
Si la carga y el momento angular son tales que la cantidad c�a� + G Q� es mayor que G�M�, los dos horizontes desaparecen y la singularidad queda al descubierto.
Por lo dem�s, el espacio-tiempo de Kerr-Newman posee cualitativamente la misma estructura que el de Kerr, por lo que la descripci�n de la secci�n anterior se aplica id�nticamente y no la repetiremos.
En este cap�tulo, hemos presentado a los hoyos negros con masa, carga el�ctrica y momento angular. El lector podr� pensar que �stos son s�lo una muestra del amplio cat�logo de hoyos negros que pueden existir en el Universo, pero veremos a continuaci�n que un hoyo negro es un objeto mucho m�s simple de lo que se podr�a esperar.
NOTAS
1 En este libro utilizamos unidades electrost�ticas
de carga. As�, la fuerza el�ctrica entre dos cargas
donde R es la distancia que las separa.
2 Es m�s com�n utilizar el par�metro a, definido como el momento angular entre la masa: a = S/M.
3 Del griego ergos, trabajo, por razones que veremos a continuaci�n.
