VI. HOYOS NEGROS, TERMODINÁMICA Y MECÁNICA CUÁNTICA

LOS TRES PARÁMETROS DE UN HOYO NEGRO

SIENDO un hoyo negro la última etapa del colapso de una estrella, debería ser un objeto sumamente complicado.

En efecto, las estrellas no son esferas perfectas: rotan, lo cual produce un achatamiento de los polos, además, poseen una estructura interna bastante complicada. A medida que una estrella se colapsa, pasa por las fases de enana blanca y estrella de neutrones, cuerpos con intensos campos magnéticos e irregularidades en sus superficies —montañas y grietas—. Así, sería de esperar que un hoyo negro posea una estructura muy compleja, heredada de las irregularidades de la estrella original, y sea, por lo tanto, un objeto muy complicado, descrito por un gran número de parámetros.

Para los fines prácticos de muchos cálculos, se puede suponer, en una primera aproximación, que un planeta es una esfera con cierta masa y cierto radio. Sin embargo, un estudio más detallado requiere del conocimiento de un gran número de propiedades, como la velocidad de rotación, el campo magnético, la estructura geológica, etc. Análogamente, la solución de Kerr-Newman con tres parámetros —masa, momento angular y carga— debería ser sólo una primera aproximación a lo que es un verdadero hoyo negro.

Después del descubrimiento del espacio-tiempo de Kerr y de su versión generalizada con carga, resurgió el interés por encontrar otras soluciones de las ecuaciones de Einstein que describan hoyos negros más complejos. Recordemos que un hoyo negro, definido matemáticamente, es un espacio-tiempo que posee un horizonte dispuesto de manera que su interior está incomunicado para siempre del exterior, mientras que el exterior tiende, a lo lejos, a un espacio-tiempo plano —ya que la fuerza de la gravedad disminuye con la distancia—. Se puede suponer, además, que el espacio alrededor de un hoyo negro se encuentra vacío; esta simplificación es válida en los casos en que la cantidad de materia en el exterior de un hoyo no influye apreciablemente sobre su estructura.

Un hoyo negro que se forme aislado en el espacio debe tender a una situación de equilibrio que ya no cambie con el tiempo. Después de un periodo de acomodo, la curvatura del espacio-tiempo permanecerá fija y no dependerá del tiempo en que se mide. El estado final, independiente del tiempo, de un hoyo negro es el más interesante en cuanto a sus propiedades físicas y el que se presta mejor a un estudio matemático.

La búsqueda matemática de los hoyos negros tomó un nuevo e inesperado giro en 1967, cuando Werner Israel encontró la demostración matemática de que el único espacio-tiempo estático (en el que no hay movimiento) que corresponde a un hoyo negro sin materia o campo electromagnético alrededor, es el espacio-tiempo de Schwarzschild. Posteriormente, el mismo Israel demostró que si se permite la presencia de un campo electromagnético, entonces el único espacio-tiempo con un hoyo negro es el de Reissner-Nordstrom.

Las implicaciones de este resultado son muy considerables. Si un cuerpo masivo no rotante, pero con una estructura muy complicada, incluyendo un campo eléctrico o magnético, se colapsa para formar un hoyo negro, el único recuerdo que quedará de él será su masa y su carga eléctrica; el campo magnético será radiado a lo lejos y quedará, finalmente, un hoyo negro descrito por la solución de Schwarzschild, o de Reissner-Nordstrom si el cuerpo estaba eléctricamente cargado.

La demostración de Israel es válida únicamente en una situación estática, en la que el hoyo negro no posee ningún tipo de movimiento. Éste no es el caso de un hoyo negro rotante, que corresponde a una situación estacionaria, mas no estática. (El movimiento estacionario es aquel que no varía con el tiempo, como, por ejemplo, el fluir constante de un líquido.) El problema que surge de una manera natural es saber si existe una restricción sobre la forma de un hoyo negro estacionario.

Dado que el espacio-tiempo de Kerr era la única solución conocida que describía un hoyo rotante, se sospechó inmediatamente que debería ser la única que corresponde a un hoyo negro estacionario. Y en presencia de un campo electromagnético, la única solución debería ser la de Kerr-Newman. La demostración de esta conjetura fue muy ardua (una primera versión se debe a B. Carter), pero finalmente se logró establecer lo que el descubrimiento de Israel hacía sospechar: El único espacio-tiempo estacionario que corresponde a un hoyo negro estacionario y rodeado por el vacío, es el espacio-tiempo de Kerr (o de Kerr-Newman, si es que hay un campo electromagnético). Esto nos lleva a la conclusión de que un hoyo negro, en una situación estacionaria, únicamente posee tres parámetros que lo describen: masa, carga y momento angular.

Este resultado sorprendente implica que una estrella en colapso se deshace de todas sus peculiaridades —estructura interna, color, achatamiento polar, campo magnético, etc.— al transformarse en hoyo negro. Más aún, se ha calculado que esta eliminación ocurre en un tiempo extremadamente corto.

Así, a diferencia de un planeta o una estrella, un hoyo negro tiene una estructura extremadamente simple. En cierto sentido recuerda a una partícula elemental que no posee estructura interna y está determinada por un número restringido de parámetros, entre los que se cuentan justamente la masa, la carga y el momento angular (o espín). John A. Wheeler ha descrito la simplicidad de los hoyos negros en palabras pintorescas: "los hoyos negros no tienen pelos", entendiéndose por "pelo" cualquier parámetro necesario para describirlo que no sea la masa, la carga o el momento angular.

(Estrictamente hablando, un hoyo negro podría poseer también una carga magnética, si existieran los monopolos magnéticos. Sin embargo, hasta la fecha no se ha encontrado una evidencia experimental que confirme definitivamente la existencia de tales objetos. Un monopolo magnético sería una partícula con una carga magnética aislada, a diferencia de un imán que siempre posee dos cargas magnéticas, o polos, inseparables.)1

Los resultados descritos hasta aquí son válidos para un hoyo negro aislado en el espacio. La situación puede cambiar si hay suficiente materia alrededor del hoyo negro para influir sobre éste, o si el hoyo se encuentra situado en un campo magnético externo (lo cual no sería improbable, ya que las galaxias suelen poseer campos magnéticos). El estudio teórico de los hoyos negros en situaciones realistas apenas ha empezado, debido a la gran complejidad matemática del problema; quizá, en el futuro, se encuentren resultados interesantes que puedan explicar ciertos fenómenos en el Universo.

LA ENTROPÍA DE UN HOYO NEGRO

Una vez formado un hoyo negro, todavía puede alterar su estado si absorbe materia que le cae desde lejos. Si esto sucede, entonces, después de un breve periodo de reacomodo, el hoyo negro regresa a un estado estacionario en el que sus tres parámetros fundamentales adquieren nuevos valores, de acuerdo con las características de la materia que absorbió. Sin embargo, la variación de los tres parámetros no es totalmente arbitraria, como veremos a continuación.

El horizonte de un hoyo negro es una superficie esférica y se puede calcular su área sin ambigñedad. En geometría clásica, el área de una esfera de radio R es . Se puede demostrar que esta fórmula se modifica ligeramente en un espacio curvo. En particular, el área A del horizonte de un hoyo negro rotante y cargado —el caso más general— resulta ser

donde r+ es el radio del horizonte externo. Más explícitamente, en términos de los tres parámetros M, a y Q el área es

En principio, se pueden alterar los parámetros de un hoyo negro arrojándole desde el exterior partículas masivas, cargadas o con momento angular. Sin embargo, tanto la carga como el momento angular implican cierta forma de energía —energía eléctrica y energía de rotación—. Debido a la equivalencia entre masa y energía, la carga y el momento angular de una partícula también contribuyen a aumentar la masa del hoyo negro que la atrapa. El resultado es que la nueva masa del hoyo negro va a depender también de la carga y el momento angular que captura, de modo tal que el horizonte no cambia en una forma totalmente arbitraria.

En 1972, el físico inglés Steven Hawking demostró un teorema matemático sobre los hoyos negros, que habría de tener hondas implicaciones. Según el teorema de Hawking, el área del horizonte de un hoyo negro puede aumentar o permanecer constante, como consecuencia de algún proceso físico, pero en ningún caso puede disminuir.

Si, por ejemplo, dos hoyos negros chocan entre sí, se fusionan para producir un nuevo y único hoyo negro. El área del horizonte del nuevo hoyo será necesariamente mayor que la suma de las áreas de los dos horizontes antes de la colisión.

El teorema de Hawking impone ciertas restricciones sobre la cantidad de energía que se puede extraer de un hoyo negro por medio de algún mecanismo, como, por ejemplo, el proceso de Penrose. Como parte de la masa de un hoyo negro se debe a su energía de rotación o a su carga, un hoyo negro puede liberar energía a costa de reducir su masa: al disminuir su carga o su momento angular. Este proceso termina cuando al hoyo negro sólo le queda una cierta masa. Así, un hoyo negro sin carga ni momento angular es un hoyo negro "inerte" en lo que se refiere a la posibilidad de extraerle energía. Por otra parte, la masa final del hoyo negro totalmente "exprimido" de energía no puede ser arbitrariamente pequeña, ya que el área del horizonte nunca disminuye. Es fácil deducir de la formula (1) que la masa final del hoyo debe ser mayor o igual que

donde A es el área inicial del hoyo.

Se puede demostrar que existe una relación precisa entre los incrementos de la masa y del área de un hoyo negro. Si el área de un hoyo negro aumenta en una cantidad , entonces la masa se incrementa en una cantidad , dada por la fórmula

donde la cantidad K es la gravedad superficial del hoyo negro; los términos adicionales en la fórmula —que carecen de importancia en el asunto que se trata a continuación— dependen del incremento en la carga y el momento angular y, son nulos, si estos parámetros no varían.

La gravedad superficial es la aceleración gravitacional producida por el hoyo negro en el sitio justo de su horizonte; su valor está dado por la fórmula:

que se reduce, en el caso de un hoyo negro sin carga ni momento angular, simplemente a

o en números,

donde M es la masa del hoyo medida en masas solares.2 En comparación, la gravedad en la superficie de la Tierra es de 9.81 m/segñ o, lo que es igual: 1 g.

Al conocer los resultados matemáticos descritos hasta aquí, los teóricos de los hoyos negros se percataron de que existe una relación entre la física de los hoyos negros y otra rama de la física, aparentemente muy alejada, que es la termodinámica. La clave fundamental es la analogía entre el área de un hoyo negro y el concepto termodinámico de la entropía.

Existen varias maneras de interpretar la entropía. Sin entrar en muchos detalles, podemos afirmar que la entropía es una medida (inversa) de la cantidad de energía que se puede extraer de un sistema físico. Consideremos, por ejemplo, una piedra que resbala sobre un plano inclinado (Figura 21). Mientras resbala, la piedra transforma su energía inicial en calor: tanto la piedra como el plano se calientan por fricción. Ahora bien, siendo el calor una forma de energía (movimiento de las moléculas), ¿podría esa energía regresar a la piedra y hacer que ésta suba sola por el plano inclinado? Sabemos por experiencia que tal fenómeno nunca ocurre. Antes de resbalar, la piedra posee una energía que se puede aprovechar —por ejemplo, arrastrando otro cuerpo consigo—; después de llegar al suelo, su energía se ha convertido en calor y es irrecuperable. La entropía es una medida de la energía irrecuperable en un sistema físico.

La llamada primera ley de la termodinámica permite relacionar el aumento de la energía interna (por ejemplo, energía en forma de calor) con el aumento de la entropía. Si es el incremento de la entropía de un cuerpo, entonces su energía interna se incrementa en una cantidad dada por la fórmula

donde T es la temperatura del cuerpo y los términos adicionales dependen de la variación de otros parámetros del cuerpo (volumen, composición, etc.).

Ahora bien, según la segunda ley de la termodinámica, la entropía de un sistema aislado siempre aumenta con el tiempo, o al menos permanece constante.³ Si el agua regada en el suelo no se vuelve a juntar y brinca espontáneamente al vaso donde estaba, es porque la naturaleza sólo permite pasar de un estado a otro cuando el estado final posee más entropía que el inicial.

La segunda ley de la termodinámica permite definir el sentido del tiempo: el tiempo corre en la dirección en que aumenta la entropía. La entropía es uno de los conceptos más interesantes y sutiles de la física. Evidentemente, un estudio más detallado rebasa los própositos de este libro.

Volviendo a los hoyos negros, podemos notar una analogía obvia entre el área del horizonte y la entropía. En primer lugar, las dos son cantidades que nunca disminuyen con el tiempo. Si, además, recordamos que la masa es equivalente a la energía, resulta que la fórmula (2), que relaciona el incremento de la masa con el incremento del área de un hoyo negro, es el análogo de la primera ley de la termodinámica (fórmula 4), que relaciona el incremento de la energía interna con el incremento de la entropía. En cuanto al teorema de Hawking sobre el área de un hoyo negro, sería exactamente equivalente a la segunda ley de la termodinámica.

Así, la entropía de un hoyo negro debe ser proporcional a su área y, siguiendo la analogía, la aceleración gravitacional en la superficie del hoyo, K, debe ser el análogo de la temperatura (compárense las fórmulas 2 y 4). (Estas propiedades físicas no deben de confundirse con parámetros nuevos o "pelos", pues están enteramente determinadas por los tres parámetros fundamentales M, a y Q. )

La analogía se puede seguir aún más lejos. Según la llamada "ley cero" de la termodinámica, un sistema físico en equilibrio completo posee la misma temperatura en todas sus partes. En el caso de los hoyos negros, se puede demostrar que la gravedad superficial tiene el mismo valor en cada punto del horizonte.

Por último, la tercera ley de la termodinámica especifica que la temperatura de cero absoluto es imposible de alcanzar. El análogo de esta ley para los hoyos negros es sumamente interesante. A partir de la fórmula (3) para K, resulta que la gravedad superficial se hace cero si los tres parámetros M, Q y a del hoyo negro cumplen la condición

Gñ Mñ = GQñ + añ cñ

Éste es justamente el caso en que, en el espacio-tiempo de Kerr-Newman, el horizonte interno y el externo se funden en uno solo. En ese caso crítico la gravedad superficial del hoyo negro se anula —pero no el área del horizonte—. Como vimos en el capítulo anterior, si la masa M es tal que Gñ Mñ es menor que GQñ + añ cñ, entonces los dos horizontes desaparecen. El análogo a la tercera ley de la termodinámica es que la gravedad superficial de un hoyo negro no puede alcanzar el valor cero. Si esto llegara a ocurrir, se podría, con la más mínima perturbación, destruir el horizonte del hoyo negro y dejar la singularidad desnuda.

Una versión más general de esta tercera ley es que ningun proceso físico puede producir una singularidad desnuda. La formación de una singularidad implica, necesariamente, la aparición de un horizonte que esconde esa singularidad de las miradas del exterior. Esta conjetura aún no ha sido demostrada rigurosamente, pero todos los estudios teóricos de la formación de hoyos negros la apoyan; Penrose ha llamado a esta posible ley natural: "censura cósmica".

A pesar de su interés, la analogía entre termodinámica y física de los hoyos negros debe tomarse con mucha cautela. El problema esencial es que no se puede asociar una temperatura real a un objeto que todo absorbe y nada emite. Todo cuerpo caliente emite radiación en alguna forma, desde ondas de radio hasta rayos gamma, dependiendo de su temperatura. Sólo un cuerpo que se encuentra a la temperatura de cero absoluto (273.16 grados centígrados bajo cero) no emite ningún tipo de radiación. Ahora bien, dado que un hoyo negro únicamente absorbe pero no emite nada, su temperatura debe ser cero absoluto. La similitud entre la gravedad superficial y la temperatura parece ser, entonces, sólo una analogía que no debe interpretarse literalmente.

Más aún, la primera ley de la termodinámica (fórmula 4), aplicada a un hoyo negro implica que, si la temperatura es cero, la entropía del hoyo negro debe ser infinita. En efecto, cualquier aumento de la energía interna del hoyo negro produce un incremento de entropía igual a /T; si T = 0, el incremento de la entropía es infinito (cualquier número dividido entre cero es infinito). Así, la analogía entre el área del horizonte y la entropía tampoco puede interpretarse sin ambigñedades.

Tal era la situación de la termodinámica y de los hoyos negros, hasta que una conexión más profunda fue descubierta al entrar en escena la mecánica cuántica.

LA RADIACIÓN DE HAWKING

La física newtoniana no puede describir fenómenos que implican velocidades cercanas (o iguales) a la de la luz, o dimensiones comparables a las de los átomos. En el primer caso —velocidades muy altas— la teoría de la relatividad toma el relevo de la física clásica; en el segundo caso —dimensiones muy pequeñas— es la mecánica cuántica la que remplaza a la mecánica newtoniana.

La mecánica cuántica surgió a principios del siglo XX con el fin de explicar algunos fenómenos que parecían contradecir los principios de la mecánica clásica. Uno de los problemas más importantes de la física de finales del siglo pasado era explicar la forma de la llamada radiación de "cuerpo negro": la luz emitida por un cuerpo caliente aislado del exterior y en perfecto equilibrio térmico.4

El gran físico alemán Max Planck logró resolver este problema con base en una suposición que, en un principio, parecía totalmente ad hoc. Planck postuló que la luz se propaga en paquetes de energía, de modo tal que cada paquete, o quantum de luz, posee una energía E proporcional a la frecuencia v; explícitamente:

E = h v

donde h es la ahora llamada constante de Planck (su valor es 6.626 X 10^{- 27}ergs x segundo) una de las tres constantes fundamentales de la naturaleza, junto con G y c.

Poco después, Albert Einstein dio un paso aún más audaz que Planck al postular que la luz está constituida de partículas, los fotones, que poseen una energía dada justamente por la fórmula de Planck. Con su hipótesis, Einstein logró explicar el efecto fotoeléctrico (lo que le valió el premio Nobel en 1920) y contribuyó, en forma decisiva, a fundar la física cuántica.

La física del mundo microscópico siguió desarrollándose rápidamente: Niels Bohr sentó las bases epistemológicas de la mecánica cuántica; Erwin Schroedinger dedujo la ecuación que lleva su nombre y que es a la física cuántica, lo que la ecuación de Newton (fuerza igual a masa por aceleración) a la física clásica; Werner Heisenberg encontró el principio de incertidumbre, según el cual es imposible medir la posición y la velocidad de una partícula con precisión absoluta; muchos más descubrimientos siguieron, pero mencionarlos nos alejaría demasiado de los propósitos de este libro...

La relatividad y la mecánica cuántica siguieron rutas separadas durante un par de décadas, sin que hubiera interacción entre ellas. Finalmente, en 1930, el gran físico inglés Paul Adrien Maurice Dirac logró formular clara y rigurosamente una teoría que unificaba la mecánica cuántica y la relatividad especial. La unión de estas dos teorías fue extremadamente fructífera; la mecánica cuántica relativista es ahora el fundamento de las teorías modernas de partículas elementales.

Empero, la relatividad general resistió todos los intentos de unirla con la mecánica cuántica. Durante décadas, los físicos teóricos trataron de elaborar, sin éxito, una teoría cuántica de la gravitación. Sólo en los años setenta empezaron a aparecer algunas pistas sobre la manera de lograr tan importante unificación, aunque la meta todavía se encuentra lejos.

En espera de que surja una verdadera teoría cuántica de la gravitación, se puede intentar extrapolar los resultados clásicos de la mecánica cuántica, que son válidos y están bien establecidos en un espacio plano, a un espacio-tiempo curvo. Este enfoque del problema equivale a suponer, en una primera aproximación, una fuerza gravitacional dada de antemano y suficientemente intensa para que no influyan sobre ella los efectos cuánticos.

Hasta aquí, nos hemos referido siempre a hoyos negros "clásicos", en el sentido de que no se incluye ningún efecto cuántico. En particular, la propiedad más importante de un hoyo negro es la de no dejar escapar nada del interior de su horizonte. Sin embargo, en 1974 Steven Hawking (Figura 44) descubrió que, si se toman en cuenta ciertos efectos cuánticos de acuerdo con la aproximación mencionada arriba, un hoyo negro emite radiación. Este resultado inesperado está relacionado al concepto de "vacío cuántico" que analizaremos más adelante. Por ahora, veamos algunas implicaciones físicas de este fenómeno.

Figura 44. El físico inglés S.W. Hawking, quien ha hecho varias contribuciones notables al estudio teórico de los hoyos negros.

Hawking demostró que un hoyo negro radia exactamente como si fuera un "cuerpo negro" en equilibrio termodinámico total (curiosamente, el mismo tipo de cuerpo caliente cuyo estudio condujo a la fundación de la mecánica cuántica). La temperatura T de un hoyo negro de masa M, sin carga ni momento angular, resulta ser

donde k es la constante de Boltzman que aparece en todos los problemas de termodinámica.5

En números, esta temperatura es

donde M es la masa del hoyo negro, medida en kilogramos.

Es importante señalar que la temperatura de un hoyo negro es inversamente proporcional a su masa. Para un hoyo cuya masa sea comparable a la del Sol, la temperatura es extremadamente baja: apenas una millonésima de grado sobre el cero absoluto; la radiación de un cuerpo a esa temperatura es completamente indetectable. Es evidente, pues, que el efecto Hawking carece totalmente de importancia para los hoyos negros que se forman por el colapso gravitacional de un estrella. En cambio, este efecto podría ser muy importante para los hoyos negros poco masivos, si es que existen; por ejemplo, un hoyo negro con una masa de cien millones de toneladas (algo así como la masa de una montaña) tendría una temperatura de casi un billón de grados Kelvin (10¹² ñK).

Como cualquier cuerpo caliente, un hoyo negro radia energía principalmente en forma de fotones —luz—, aunque también emite otras partículas si la temperatura es suficientemente alta: neutrinos, electrones, positrones, etc. Así, un hoyo negro radia, a costa de perder su propia energía o, lo que es equivalente, su masa. A medida que la masa del hoyo negro disminuye, su temperatura aumenta y la radiación se hace más intensa. Consecuentemente, la masa disminuye cada vez más y más rápidamente, hasta que el hoyo negro se evapora totalmente en una verdadera explosión.

Se puede calcular el tiempo que tardaría un hoyo negro en evaporarse por completo; este tiempo resulta ser del orden de

o, aproximadamente, 10^-17 M³ segundos, si la masa M se mide en kilogramos. Un hoyo negro de una masa comparable a la del Sol se evaporaría, según esta fórmula, en ñ10⁶⁷! (en comparación, la edad del Universo es de unos 10¹⁰ años). Como mencionamos anteriormente, el efecto Hawking es totalmente insignificante para los hoyos negros muy masivos.

Para un hoyo negro de masa modesta, por ejemplo unas cien millones de toneladas, el tiempo de evaporacíón resulta ser de unos 10¹⁰ años, comparable a la edad del Universo. Como vimos en el capítulo IV, es posible que se hayan formado hoyos negros con masas relativamente pequeñas en los primeros instantes del Universo. Un hoyo negro primordial que nació en esas épocas remotas con una masa de cien millones de toneladas se encontraría en la actualidad justamente en la fase final de evaporación. Debido a su altísima temperatura, tal hoyo negro se observaría como una intensa fuente de rayos gamma, que es el tipo de radiación emitida por un cuerpo a varios miles de millones de grados. Por otra parte, los astrónomos han detectado, desde hace tiempo, un gran número de fuentes de rayos gamma en el Universo. En muchos casos, el mecanismo físico que produce estos rayos se ha podido identificar plenamente y no corresponde a un hoyo negro en evaporación. Sin embargo, queda como un problema pendiente determinar si algunos rayos gamma detectados en la Tierra han sido producidos por la explosión de hoyos negros primordiales.

El hecho de que un hoyo negro posea realmente una temperatura permite reformular consistentemente las ideas de la sección anterior sobre la "termodinámica" de los hoyos negros. El descubrimiento de Hawking puso en evidencia que la analogía entre temperatura y gravedad superficial no es puramente formal. La temperatura T se puede relacionar sin ambigñedad con la gravedad superficial K de un hoyo negro con masa, carga y momento angular, por medio de la relación

donde K está dada por la fórmula (3). Más aún, el hecho de que un hoyo negro tenga una temperatura distinta del cero absoluto implica una relación precisa entre la entropía y el área del horizonte; la entropía del hoyo negro resulta ser:

donde el área A está dada por la fórmula (1).

La temperatura y la entropía de un hoyo negro se deben a efectos puramente cuánticos, como se desprende claramente del hecho de que la constante de Planck h aparece en las fórmulas (6) y (7). Despreciar los efectos cuánticos, como se hace en la física "clásica", equivale a asignar el valor cero a la constante de Planck en una primera aproximación. La temperatura de un hoyo negro es proporcional a h, mientras que su entropía es proporcional a 1/h; si h fuera estrictamente cero, la temperatura sería cero absoluto y la entropía infinita: tal como se esperaría si no existieran los efectos cuánticos.

Finalmente, señalemos que la evaporación y eventual desaparición de un hoyo negro no contradice la segunda ley de la termodinámica: si bien el área —entropía— del hoyo disminuye, la radiación producida posee una entropía muy alta, de modo tal que la entropía total aumenta.

EL VACIO CUÁNTICO

El efecto descubierto por Hawking puede parecer contradictorio a primera vista. Si nada sale de un hoyo negro, como se ha repetido insistentemente, ¿cómo es posible que el hoyo radie energía? La radiación de un hoyo negro es un fenómeno íntimamente relacionado con uno de los problemas más formidables de la física moderna: el concepto de vacío.

Antes de que apareciera la mecánica cuántica, el vacío era un concepto trivial: significaba la ausencia total de materia o energía. Sin embargo, la situación ha resultado ser mucho más complicada a nivel cuántico.

El origen del problema se encuentra en el principio de incertidumbre de Heisenberg, que ya tuvimos ocasión de mencionar. Este principio fundamental de la mecánica cuántica establece un límite intrínseco a la precisión con que se pueden medir simultáneamente la posición y la velocidad de una partícula. Una forma equivalente de este principio impone una restricción similar sobre la posibilidad de medir la energía de una partícula y el momento en que se efectúa la medición. Supongamos que es el error en la medición de la energía y el error en la medición del tiempo.⁶

Según el principio de incertidumbre, los errores no pueden ser arbitrariamente pequeños sino que deben satisfacer la desigualdad

independientemente de cuán precisas sean las mediciones.

Al combinar este principio con la equivalencia entre energía y masa predicha por la relatividad, nos encontramos con el resultado sorprendente de que se puede crear materia a partir del vacío. Una partícula puede aparecer súbitamente y desaparecer acto seguido. Esto no puede ocurrir según la física clásica —la materia no se crea de la nada—, pero sí es factible según la física cuántica, a condición de que el tiempo de vida de la partícula sea suficientemente corto. En efecto, una partícula de masa M posee una energía Mcñ; si su tiempo de vida es menor que h/mcñ, entonces, de acuerdo con el principio de incertidumbre, la partícula no puede ser detectada: durante ese lapso, la masa (energía) de la partícula se encuentra por debajo del margen de error con que se podría medir, aun con el detector más sensible.

Así, el "vacío" de la mecánica cuántica está repleto de partículas que aparecen y desaparecen burlándose de la ley de conservación de la masa, encubiertas por el principio de incertidumbre de Heisenberg. Tales partículas, por principio indetectables, se llaman partículas virtuales.

No todas las cantidades físicas satisfacen el principio de incertidumbre; por ejemplo, la carga eléctrica se puede determinar sin restricciones, dependiendo la precisión únicamente de la calidad de los métodos de medición utilizados. En consecuencia, una partícula cargada no puede surgir de la nada, porque podría detectarse y violaría el principio de que la carga eléctrica siempre se conserva.

Sin embargo, todas las partículas elementales existen en forma de partículas o antipartículas; la carga eléctrica de una antipartícula es de signo contrario al de su partícula correspondiente, siendo las masas iguales. Es posible, entonces, que una partícula y su antipartícula surjan de la nada y desaparezcan sin poder ser detectadas, porque la carga eléctrica de la pareja sería cero y no se habrá violado el principio de conservación de la carga eléctrica. Así, por ejemplo, puede surgir del vacío un par virtual formado por un electrón y un positrón, los cuales deben desaparecer en un tiempo menor que h/2 Mcñ (siendo m la masa del electrón o positrón), tiempo que equivale a unos 10^-22 segundos.

La presencia de partículas virtuales en el vacío ocasiona una serie de problemas conceptuales que los físicos aún no han podido resolver satisfactoriamente. La dificultad fundamental es que la energía del vacío es formalmente infinita, ya que se pueden crear partículas virtuales con energías ilimitadas. Por otra parte, el vacío cuántico no es un concepto metafísico: las partículas virtuales no pueden observarse directamente, pero producen una serie de efectos reales que se pueden medir experimentalmente. Uno de los mayores retos para los físicos teóricos en la actualidad es comprender y manejar satisfactoriamente el concepto del vacío cuántico.

Justamente, la radiación de los hoyos negros es un efecto producido por la gravedad sobre el vacío cuántico. El mismo Hawking propuso una interpretación, en términos comprensibles, del efecto descubierto por él: dado que la fuerza de gravedad varía con la distancia, un cuerpo masivo influye desigualmente sobre otro cuerpo masivo: las partes más cercanas al cuerpo atractor son atraídas más intensamente que las partes más alejadas. Este efecto se conoce como fuerza de marea; es el mismo que produce una deformación de los océanos terrestres, porque la Luna atrae más fuertemente a la parte de la Tierra cercana a ella. Evidentemente, los hoyos negros también inducen fuerzas de marea sobre los cuerpos cercanos a ellos. Supongamos que un par formado por un electrón y un positrón virtuales se crea muy cerca de un hoyo negro. Hawking señaló que la fuerza de marea puede romper el par, de modo tal que las dos partículas se vuelven reales y una cae al hoyo, mientras que la otra escapa a lo lejos (Figura 45). La partícula que escapa lleva consigo parte de la energía gravitacional del hoyo y, es esa energía liberada, la que produce la radiación.

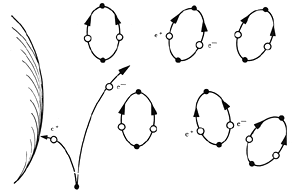
Figura 45. Un par virtual creado cerca de un hoyo negro puede desgarrarse por la fuerza de marea.

Otra posible interpretación del efecto Hawking es en términos de una alteración de la energía del vacío cuántico. Hemos señalado anteriormente que la energía de una partícula se modifica por la atracción gravitacional; una de las consecuencias más importantes de este fenómeno es que la luz emitida cerca de un objeto masivo se enrojece (pierde energía). Se puede demostrar que este mismo fenómeno, aplicado a la energía del vacío cuántico cerca de un hoyo negro, produce una alteración de esta energía que, en términos cuantitativos, hace que la región alrededor del hoyo negro adquiera una temperatura exactamente igual a la predicha por Hawking. Según esta interpretación alternativa, un hoyo negro no radia energía sino que deforma la energía del vacío cuántico.

Aún quedan muchos problemas que resolver con respecto a la radiación de los hoyos negros. Probablemente, la situación se aclarará cuando dispongamos de una verdadera teoría cuántica de la gravedad. Mientras, el efecto descubierto por Hawking nos indica que debemos prepararnos a múltiples sorpresas. En particular, la posibilidad de que existan hoyos negros microscópicos que se evaporan rápidamente complica aún más el concepto del vacío cuántico: así como se forman partículas virtuales, se pueden crear hoyos negros virtuales a partir del vacío. Si la masa de un hoyo negro no excede de unos 10^-5 gramos (que es el valor aproximado de 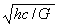), se evaporará en unos segundos (que corresponde al valor de 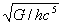). El lector puede comprobar que el producto de la energía (masa X cñ) y el tiempo de vida de tal hoyo negro es menor que h. En consecuencia, gracias al principio de incertidumbre de Heisenberg, los hoyos negros con masas menores que unos gramos pueden crearse de la nada y evaporarse sin violar la ley de conservación de la masa.

El máximo radio que puede tener un hoyo negro virtual está dado aproximadamente por

que equivale a unos 10-ññ centímetros. Esta distancia se conoce como longitud de Planck y es la única unidad de distancia que se puede construir con las tres constantes fundamentales de la naturaleza: G, h y c. La longitud de Planck es tan extremadamente pequeña (10ññ veces menor que el radio de un electrón) que debe ser la distancia característica de otro nivel de la naturaleza, subyacente al mundo subatómico, donde rigen las leyes aún desconocidas de la gravedad cuántica.7

Así como el océano presenta un aspecto liso e inmóvil cuando se observa desde una gran distancia, pero posee fuertes turbulencias y tormentas a escala humana, el espacio-tiempo parece "liso" y estático a gran escala, pero es extremadamente turbulento en el nivel de la longitud de Planck, donde los hoyos negros se forman y evaporan continuamente (Figura 46). En el mundo de Planck, las leyes de la física deben ser muy distintas de las que conocemos hasta ahora.

Figura 46. La estructura macroscópica del espacio-tiempo parece plana, pero éste debe ser extremadamente turbulento en el nivel de la escala de Planck.

 

NOTAS

1 Ver J. Flores La gran ilusión I. El monopolo magnético, vol. 11 de la Ciencia desde México, FCE, 1986.

2 En la física clásica, la aceleración gravitacional en la superficie de una esfera de masa M y radio R es GM/Rñ. Dado que el radio de un hoyo negro es proporcional a su masa, resulta que la aceleración gravitacional en su superficie es proporcional a GM/Mñ= G/M, tal como en la fórmula para K. Mientras más pequeño es un hoyo negro, mayor es la fuerza gravitacional en su superficie.

3 Si el sistema no está aislado e intercambia energía con otros sistemas, hay que considerar la entropía total de todos los sistemas que, en conjunto, estén aislados.

4 Por ejemplo, un recipiente cerrado de paredes calientes, perfectamente aislado.

5 K=1.38 X 10^-16 ergs/grados Kelvin.

6 Es decir si E es la energia medida, sólo se puede asegurar que la energia real se encuentra, muy probablemente, entre E —DE y E + DE. Lo mismo para t y Dt...

7 En los últimos años ha habido mucho interés en la teoría de las supercuerdas, que pretende describir la materia a la escala de Planck. Aún es temprano para juzgar este programa de investigación.