II. LOS SUPERCONDUCTORES IDEALES
TAMBI�N correspondi� a Heike Kamerlingh Onnes observar que a cualquier
temperatura T, tal que T < Tc el estado
superconductor pod�a ser destruido por la aplicaci�n de un campo magn�tico con
intensidad mayor que cierto campo magn�tico cr�tico. Por otro lado, tambi�n
not� que a cualquier temperatura T < Tc en ausencia
de un campo magn�tico, el estado superconductor pod�a destruirse aumentando
la corriente por arriba de un valor cr�tico y, asimismo, que la temperatura
de transici�n superconductora, Tc disminu�a cuando
la corriente que pasaba por el superconductor crec�a. Los efectos de las corrientes
el�ctricas y de los campos magn�ticos sobre el estado superconductor no son
ajenos entre s�, ya que la disminuci�n del valor de Tc, con
el aumento de la corriente, se debe al campo magn�tico que la corriente produce.
Experimentalmente se encuentra que el valor del campo cr�tico depende de la temperatura, cayendo de un valor Ho, a temperaturas muy bajas, hasta un valor de cero para la temperatura de transici�n Tc. Los datos experimentales revelan que la variaci�n del campo cr�tico con la temperatura queda bastante bien descrita (dentro de 2% o 3%) por una par�bola de la forma:
|
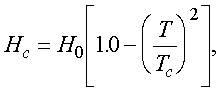
(1) |
donde Hc es el campo magn�tico cr�tico y Ho es el campo cr�tico extrapolado al cero absoluto. Cada material puede ser caracterizado por sus valores de Tc y de Ho y, conociendo �stos, se puede utilizar la ecuaci�n (1) para encontrar el campo cr�tico a cualquier temperatura.
Es de hacer notar que las curvas experimentales de la variaci�n del campo cr�tico
con la temperatura no son exactamente par�bolas y para describirlas de una manera
m�s precisa de la ya se�alada se requerir�a un polinomio en potencias de la
temperatura, que en general es de grado diferente de 2. Para la mayor�a de los
c�lculos es suficiente con utilizar la ecuaci�n (1).
CUADRO 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nb3 Al
|
18.80 x 104
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tl2 Ba2 Ca2 Cu3
O10
|
220.0 x 104
|
|
|
|
El cuadro 2 muestra los valores del campo cr�tico de algunas sustancias para el valor extrapolado a T = 0 K.
Hemos visto en el cap�tulo anterior que, en virtud del efecto Meissner-Oschenfeld, el estado de magnetizaci�n de un material en el estado superconductor depende s�lo de la temperatura de la muestra y del campo magn�tico aplicado, y no de la manera en que se llega a esos valores.
Es posible, por tanto, aplicar argumentos termodin�micos al estudio del comportamiento de un material en el estado superconductor utilizando como variables la temperatura y el campo magn�tico.
Sabemos que para comprimir un gas en el interior de un cilindro a presi�n constante tenemos que realizar un trabajo DW = PDV, donde P es la presi�n y DV es el cambio en el volumen del gas contenido en el cilindro. Del mismo modo, cuando aplicamos un campo magn�tico a una muestra el trabajo realizado por unidad de volumen de la muestra es DW = -HdM, el signo menos s�lo indica que cuando la magnetizaci�n aumenta (dM >0 ) el trabajo se est� realizando sobre el sistema.
Con lo anterior se puede encontrar f�cilmente el cambio en la energ�a libre del material al pasar de un estado a otro. Este cambio est� dado por el trabajo realizado por el campo magn�tico aplicado a la muestra. Se encuentra que la cantidad requerida de energ�a, a temperatura constante, para destruir el estado superconductor, y cuando en el estado inicial existe un campo magn�tico aplicado, es:
 |
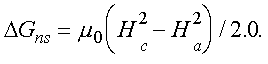(2)
|
En la ecuaci�n (2), mo, es una constante que vale 4p X 10-7 henry / metro y es la constante de permeabilidad magn�tica del vac�o; Hc es el campo magn�tico cr�tico para una temperatura dada y DGns es el cambio en la energ�a de la muestra al pasar del estado superconductor al estado normal, por medio de la aplicaci�n de un campo magn�tico.
Si inicialmente el campo magn�tico aplicado es cero, Hc = 0, y la ecuaci�n (2 nos da, para este caso, la energ�a total requerida para destruir el estado superconductor, tendremos que, por unidad de volumen, la diferencia de energ�a entre el estado normal y el estado superconductor es m0Hc(T)2 /2. Para tener una idea de la magnitud de la energ�a, hallemos su valor para el plomo y el aluminio. Si suponemos T = 0, para plomo, Hc(0) = 803 Gauss y
Es muy ilustrativo pasar esta energ�a a ev / �tomo, para comparar con las energ�as t�picas de las part�culas en el material. Tenemos que hallar el n�mero de part�culas de plomo en 1 cm3. Para esto, recordemos que 1 mole de Pb tiene 207 gr y que la densidad del plomo es de 11.4 gr/cm3. Por otro lado, el n�mero de Avogadro es 6.03 x 1023 �tomos/mole. Con estos datos encontramos que en, 1 mole de plomo hay 3 X 1022 �tomos aproximadamente. De aqu� que:
Ahora bien, la energ�a t�pica de un electr�n en el interior de un metal se puede tomar como la energ�a de Fermi para ese metal. Para Pb es de aproximadamente 5 ev.
| Por otro lado, la energ�a t�pica de un ion en el material se puede tomar
como KBQD,donde
<I>K<sub>B</sub></I><b> </b>es la constante
de Boltzmann y <font face="Symbol"><b>Q</b></font><b><sub><i>D</i></sub></b>
es una constante t�pica del material que se llama la temperatura de Debye.
|
Para Pb la energ�a t�pica de un ion resulta ser de 10 ev.
De lo anterior podemos darnos cuenta de que la energ�a involucrada en la transici�n superconductora es mucho menor que la energ�a t�pica de una part�cula en el metal.
Veamos ahora el caso del aluminio. Para este metal la energ�a de transici�n al estado superconductor es de 1.4 x 10-9 ev/�tomo. La energ�a de Fermi para aluminio es de 1 ev aproximadamente y la energ�a t�pica de un ion resulta ser de 5.91 x 10-2 ev/�tomo. Nuevamente vemos que la energ�a de transici�n al estado superconductor, por part�cula, resulta ser mucho menor que las energ�as t�picas de las part�culas en el metal.
La magnitud de la energ�a para la transici�n al estado superconductor fue una de las pautas para el establecimiento de una teor�a microsc�pica de la superconductividad.
Sabemos, a partir de la termodin�mica, que una medida del orden o del desorden en un sistema, la da el valor de la entrop�a. Si un sistema en un estado dado tiene un valor para la entrop�a mayor que el valor para el mismo sistema en otro estado, se dice que el segundo estado es m�s ordenado que el primero. De este modo, si los iones de un metal presentan un arreglo peri�dico, este estado tendr� menor entrop�a (y por tanto mayor orden) que el metal en estado l�quido.
Una de las primeras preguntas que surgieron cuando se descubri� la superconductividad fue si el estado superconductor es m�s ordenado (o desordenado) que el estado normal; se puede responder estimando el cambio en la entrop�a del material al pasar del estado normal al estado superconductor. Haciendo unos c�lculos termodin�micos sencillos se puede demostrar que el cambio en el valor de la entrop�a por unidad de volumen al pasar del estado superconductor al estado normal, DSns, est� dado por:
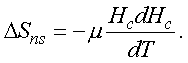
Ahora bien, podemos hacer uso de la expresi�n de la variaci�n del campo magn�tico cr�tico en funci�n de la temperatura para hallar dHc /dT, ecuaci�n (1) y obtenemos que:
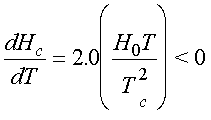
y por tanto, DSns > 0, lo cual significa que la entrop�a en el estado superconductor, es menor que la entrop�a en el estado normal.
En otras palabras, el estado superconductor es m�s ordenado que el estado normal del material. Sin embargo, ya vimos anteriormente que una de las propiedades del material que no cambia al pasar al estado superconductor es la estructura cristalina, lo que significa que el mayor ordenamiento que se presenta en el material al pasar al estado superconductor no se debe a un mayor ordenamiento de la red cristalina, ya que �sta no sufre cambio alguno. El ordenamiento tiene que ser de la otra componente del material, de la parte que corresponde a los electrones. Podemos esperar que los electrones lleguen a un estado de mayor ordenamiento del que tienen en estado normal. Este hecho tambi�n dio una pauta para el establecimiento de una teor�a microsc�pica de la superconductividad.
Al igual que en un metal en el estado normal, el calor espec�fico de un metal en el estado superconductor consiste, b�sicamente, en una contribuci�n de la red de iones del metal (o red cristalina), Cr, y una contribuci�n electr�nica, Cel. De este modo, siC es el calor espec�fico de un metal en el estado normal: C = Cr + Cel. A bajas temperaturas se tiene que Cel = gT donde g es una constante para cada material, T es la temperatura medida en Kelvin y Cr = A(T /QD)3, donde A es una constante num�rica para todos los metales y QD es la temperatura de Debye.
Experimentalmente se encuentra que la contribuci�n electr�nica al calor espec�fico en el estado superconductor est� dada por:
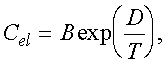
donde B y D son constantes del material.
Esta variaci�n exponencial de la contribuci�n electr�nica al calor espec�fico es radicalmente distinta de la correspondiente en el estado normal y tambi�n, por cierto, t�pica de la contribuci�n electr�nica al calor espec�fico de un material semiconductor. �sta era otra indicaci�n de que algo extraordinario estaba ocurriendo con los electrones al pasar el material al estado superconductor. Esta variaci�n del calor espec�fico, en su parte correspondiente a los electrones, tambi�n sent� una importante pauta para el establecimiento de una teor�a microsc�pica de la superconductividad.
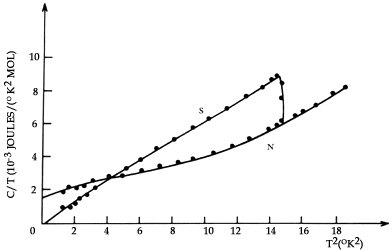
Figura 7. Variaci�n del calor espec�fico del esta�o. El campo magn�tico aplicado es cero para el caso superconductor, S. El campo magn�tico aplicado es mayor que el campo magn�tico cr�tico para el caso normal, N, como funci�n de la temperatura. N�tese el salto en el valor del calor espec�fico.
Una indicaci�n de que los iones del metal influyen de alguna manera en el cambio de comportamiento de los electrones al pasar al estado superconductor la dio el que fue llamado efecto isot�pico. Para entenderlo, recordemos que un is�topo es una variedad de un elemento qu�mico que, teniendo el mismo n�mero de protones, en el n�cleo at�mico, difiere del elemento qu�mico en el n�mero de neutrones que se encuentran en el mismo n�cleo. El efecto isot�pico, descubierto en 1950, consiste en que, para un mismo elemento, la temperatura cr�tica var�a de una manera que es inversamente proporcional a la ra�z cuadrada de la masa del is�topo de ese elemento. As�, aunque la red at�mica misma no muestra ning�n cambio en los superconductores ideales, result� muy claro que deb�a desempe�ar un papel importante en el cambio de comportamiento de los electrones de conducci�n en el metal.
De lo que hemos visto anteriormente es claro que algo ha de ocurrir con los electrones del material en estado normal para que se d� el paso al estado superconductor, algo que los vuelva superelectrones, de manera que nada los disperse dentro del material. Pero es claro que no dejan de ser electrones, ya que al subir la temperatura por arriba de la temperatura cr�tica del material, al aplicar un campo magn�tico con una intensidad mayor que la del campo magn�tico cr�tico correspondientes, o al aplicar una corriente por arriba de la corriente cr�tica, el material vuelve a su estado normal y, por tanto, tambi�n los electrones.
Para entender c�mo podemos tener superelectrones, imagine que va caminando por un sendero que presenta obst�culos a su paso: grandes pedruscos, agujeros, etc. Le cuesta trabajo avanzar pues cae al tropezar con los diversos obst�culos, o bien los tiene que rodear. Existe una resistencia a su avance, pues resulta lento y penoso y le cuesta mucha energ�a, tanto m�s como mayor n�mero de obst�culos tenga que superar. Ahora suponga que no camina solo, sino en parejas. As�, cuando un miembro de la pareja caiga en un bache, el otro lo ayudar� a salir y podr�n reanudar su marcha. As�, brazo con brazo, ser� m�s f�cil sortear los obst�culos del camino. Claro que puede darse el caso en que ambos caigan v�ctimas de sendos obst�culos y su avance se vea totalmente frenado, al menos por un tiempo breve. Ahora supongamos que en lugar de avanzar en parejas lo hace en tercetos, en cuartetos, en quintetos, etc. Ser� a�n m�s dif�cil que el terceto, cuarteto, el quinteto, etc., sea detenido en su camino, porque tendr�an que caer todos los elementos del conjunto simult�neamente, v�ctimas de los obst�culos. Como consecuencia, al trasladarse brazo con brazo los m�s que se puedan; disminuir� la resistencia a nuestro avance.
Lo se�alado en el p�rrafo anterior puede considerarse v�lido para el caso de los electrones y la manera de disminuir la resistencia del material a su paso. Podemos pensar que los superelectrones son los electrones en un estado en el que se encuentran unidos entre s� en grandes conjuntos para su avance en el material, de manera que no pueden ser dispersados por nada dentro de �l. As�, podemos decir que la transici�n al estado superconductor lleva a los electrones a amarrarse en grandes enjambres que no encuentran resistencia a su paso por el material, que nos lleva a un estado en el que los electrones se atraen mutuamente. �Es esta atracci�n entre dos electrones posible? La respuesta es s� y la analizaremos con m�s detalle en la siguiente secci�n.
En esta secci�n se dar� un argumento de plausibilidad acerca de la ocurrencia de una interacci�n atractiva entre dos electrones en el metal y se presentar� un resumen de lo que se conoce como el Par de Cooper, que constituy� el paso te�rico que abri� el camino hacia la teor�a microsc�pica de la superconductividad dada por Bardeen, Cooper y Schrieffer en 1957.
Veamos primero c�mo est� constituido el metal cristalino (recu�rdese que el t�rmino cristalino se refiere al hecho de que existe en el metal un arreglo peri�dico de los iones que lo constituyen). Tenemos iones y electrones. Los iones son los �tomos, inicialmente neutros, del elemento, pero desprovistos de sus electrones m�s exteriores, de manera que el resto, esto es, el n�cleo y los dem�s electrones que permanec�an ligados, constituyen los iones en el metal. Queda claro, por tanto, que los iones tienen carga positiva.
Surge la pregunta de c�mo ese conjunto de iones positivos que presentan repulsiones de tipo coulombiano, por tener el mismo signo de carga, puede constituir una estructura estable. La respuesta radica en el papel de los electrones en el metal. Los electrones, que cada �tomo cedi� para formar el metal, son compartidos por todos los iones. De esta manera, los electrones pueden viajar libremente por el metal a trav�s de los iones positivos.
Los electrones, que forman un gas dentro del metal enmascaran o apantallan
la carga de cada ion positivo; de esta manera, cada ion positivo se siente atra�do
hacia una nube de carga negativa y la interacci�n efectiva entre los iones,
mediada de este modo por los electrones; resulta de atracci�n. Claro que para
separaciones muy cortas entre los iones, la nube electr�nica que rodea a cada
ion es muy delgada, de manera que la nube electr�nica no alcanza a enmascarar
(o a apantallar) la carga del ion, y la interacci�n, para estas distancias cortas
entre dos iones, es de repulsi�n. En la figura 8 vemos una gr�fica del potencial
efectivo de interacci�n t�pico en funci�n de la distancia, para dos iones en
un metal. Existe un m�nimo en la energ�a de interacci�n que es mucho m�s profundo
que los dem�s m�nimos presentes. Este m�nimo corresponde usualmente a la separaci�n
de equilibrio de los iones. Alrededor de este m�nimo se encuentran vibrando
los iones del metal, en constante agitaci�n.
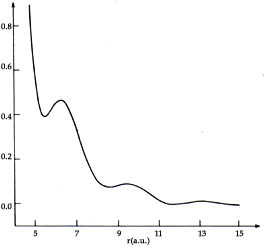
Figura 8. Potencial efectivo de interacci�n t�pico entre dos iones de metal.
En este caso el metal es aluminio. El c�lculo, de primeros principios de esta
interacci�n se realiz� en el Instituto de F�sica de la UNAM.
Es usual, en el estudio de los s�lidos, utilizar lo que se llama la aproximaci�n arm�nica.
Esta consiste, fundamentalmente, en hacer un desarrollo
en serie de Taylor del potencial de la interacci�n efectiva entre una
pareja de iones en el metal. De esta manera, si V(R) es el potencial
de interacci�n entre dos iones del metal y hacemos el correspondiente
desarrollo, alrededor de la posici�n de equilibrio que llamaremos R0:
|
| V(R) = V(R0) + V'(R0) (R - R0) + V'' (R0) (R - R0)2 /2+ ..., |
donde V' (R0), V"(R0)
son, respectivamente, la primera y la segunda derivadas del potencial
con respecto a la separaci�n de los iones calculadas en la posici�n de
equilibrio, R0. Si suponemos oscilaciones peque�as alrededor
de la posici�n de equilibrio (lo cual puede satisfacerse para temperaturas
lejanas y por abajo de la temperatura de fusi�n del metal), podemos despreciar
todos los t�rminos de grado superior a 2. Por otro lado, dado que en R0
existe un m�nimo, V'(R0) = 0, obtenemos que:
|
 |
Pero V(R0) es una
constante y el origen de medici�n del potencial puede ser elegido a nuestro
arbitrio. Escojamos el origen de modo que V(R0)
sea cero. As�: |
| V(R) = V''(R0)(R - R0)2 /2 |
y
esta expresi�n corresponde al potencial producido por un resorte, esto
es, el potencial de un oscilador arm�nico. |
Podemos decir que, a temperaturas convenientes (muy por debajo de la temperatura
de fusi�n del material), la forma efectiva en que dos iones interact�an dentro
del metal es semejante a si estuvieran unidos por un resorte. Con esto queda
claro el significado de la aproximaci�n arm�nica. Dentro de esta aproximaci�n
podemos imaginar al metal como un arreglo peri�dico de iones donde cada ion
queda unido a otro por medio de un resorte, como se muestra en la figura 9.
De este modo la red queda como un arreglo tridimensional de osciladores arm�nicos.
As�, las propiedades din�micas de la red de iones en el metal puede ser estudiada
analizando las propiedades din�micas de la red tridimensional de osciladores
arm�nicos acoplados (figura 9). Se sabe, de la mec�nica cl�sica, que este tipo
de arreglos de osciladores, al igual que la cuerda vibrante de una guitarra,
presenta modos normales de vibraci�n. Recu�rdese que un modo normal de vibraci�n
es una manera de vibrar del sistema en el cual todas las part�culas oscilan
con la misma frecuencia. Cuando se hace el an�lisis, siguiendo los m�todos de
la mec�nica cu�ntica, de la din�mica de la red de osciladores arm�nicos, se
encuentra que la energ�a de vibraci�n est� cuantizada. El cuanto (en lat�n quantum)
de energ�a de vibraci�n del arreglo tridimensional de osciladores recibe el
nombre de fon�n, en analog�a al de fot�n, que corresponde al cuanto
de vibraci�n del campo electromagn�tico que da origen a la radiaci�n luminosa.
De esta manera, cuando hablemos de fonones, nos estaremos refiriendo a la energ�a
de vibraci�n de la red de iones de la red cristalina
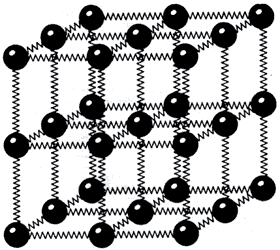
Figura 9. Esquema que representa la aproximaci�n arm�nica para un s�lido.
Resulta claro que cuando hablamos de la interacci�n electr�n-fon�n estaremos,
en esencia, hablando de las colisiones de los electrones con los iones, puesto
que al chocar los electrones con los iones se generan vibraciones en el arreglo
tridimensional de osciladores.
Por otro lado, las oscilaciones en la gr�fica de
la interacci�n efectiva entre dos iones mostrada en la figura 8, para
distancias grandes (mayores que la correspondiente al primer m�nimo) tienen
una frecuencia bien definida e igual a 2KF donde KF
es el vector de onda de Fermi. |
Estas oscilaciones, que se deben al apantallamiento
electr�nico, reciben el nombre de oscilaciones de Friedel en honor a quien
las estudi� por primera vez. |
De lo se�alado anteriormente para la interacci�n efectiva entre iones, resulta muy claro c�mo los iones de la red cristalina pueden llegar a tener una interacci�n efectiva de atracci�n por la acci�n de los electrones y presentar, de este modo una estructura estable para el metal.
Si ahora nos preguntamos c�mo podemos llegar a tener una interacci�n de atracci�n entre los electrones de un metal para alcanzar el estado superconductor, de manera natural pensaremos que tiene que ocurrir por la acci�n de los iones de la red cristalina. Esta conclusi�n se ve reforzada por la existencia del efecto isot�pico, que ya hemos mencionado en una secci�n anterior.
Sabemos que en el vac�o existe una repulsi�n entre electrones. En el interior
de un metal, como ya vimos, tenemos un gas de electrones. De esta manera la
interacci�n electr�n-electr�n se da en presencia de todos los dem�s electrones
de conducci�n (o sea, los que tienen libertad de desplazarse por el metal, los
que no est�n ligados a los n�cleos). La presencia de los dem�s electrones es
tomada en cuenta, con razonable precisi�n al estudiar los s�lidos, a trav�s
de las aproximaciones conocidas como teor�a de perturbaciones y teor�a de respuesta
lineal, por la utilizaci�n de una funci�n diel�ctrica. La funci�n diel�ctrica
sirve para tomar en cuenta el efecto de apantallamiento electr�nico.
Aunque el signo de la interacci�n, no cambia, sino que sigue siendo repulsiva. As� queda muy claro que si es posible una interacci�n de atracci�n entre dos electrones en el metal, deberemos examinar el efecto de la red de iones sobre los electrones.
Consideremos primeramente un electr�n que viaja a trav�s de la red cristalina,
como se muestra en la figura 10. Este electr�n va tirando de cada ion positivo
a su paso, generando una onda de perturbaci�n en la red. Ahora veamos con m�s
detalle a un electr�n dentro de la red cristalina (figura 10). Este electr�n
mover� hacia �l a los iones vecinos creando, localmente, un aumento en la densidad
de carga positiva, de manera tal que otro electr�n que pase por la vecindad
de esta regi�n podr� ser atra�do por el desbalance de carga positiva existente.
Tendremos as� que la interacci�n efectiva entre los dos electrones es de atracci�n,
por la mediaci�n de la red. Podemos pensar que la interacci�n electr�n-fon�n-electr�n
puede ser responsable de una interacci�n de atracci�n entre dos, electrones.
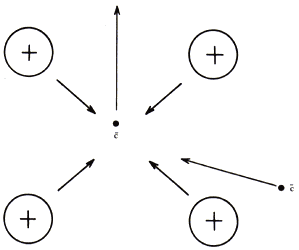
Figura 10. Electr�n que, al viajar, puede atraer a otro electr�n por medio
de la red de iones con lo cual puede dar lugar a un par de Cooper.
De hecho, en 1956 L. N. Cooper demostr� que, de existir una interacci�n atractiva entre dos electrones en un metal, estos electrones pueden permanecer ligados el uno con el otro. Tambi�n demostr� que el radio del estado ligado de los dos electrones es del orden de 104 (varios miles de distancias interi�nicas en la red cristalina), que es, pr�cticamente, una magnitud microsc�pica.
Si pudi�ramos llegar a un estado del material en que existieran pares de Cooper,
es claro que tendr�amos un superconductor ya que, por su enorme tama�o, habr�a
una enorme cantidad de traslapes entre los pares de Cooper, cre�ndose gigantescos
enjambres de electrones unidos que no ver�an resistencia a su paso.
En relaci�n con la atracci�n entre dos electrones
como paso hacia el estado superconductor, en 1956 L. N. Cooper estudia
y resuelve el siguiente problema, que marc� un paso muy importante en
el entendimiento de la superconductividad y que es conocido actualmente
como el par de Cooper. |
Cooper se pregunta que ocurrir�a si a un sistema
de electrones que se encuentra llenando el mar de Fermi (recordemos que
el mar de Fermi se refiere al conjunto de estados electr�nicos ocupados
hasta el nivel de la energ�a de Fermi), le a�adi�ramos dos electrones
m�s, con la suposici�n de que los electrones del mar de Fermi se mantuvieran
r�gidamente en sus estados, de manera que estos estados no puedan ser
accesibles; es decir, que est�n prohibidos a los dos electrones adicionales
por el principio de exclusi�n de Pauli. En otras palabras, en este problema
se toma un mar de Fermi pasivo, o sea, no se hace caso de todas las interacciones
y perturbaciones que dos electrones adicionales pudieran tener en los
electrones que ocupan el mar de Fermi. |
El problema del par de Cooper constituye un problema
ideal que, sin embargo, contiene todos los ingredientes importantes involucrados
en el problema de la superconductividad. Constituye, esencialmente un
problema de dos cuerpos que, sin embargo, toma en cuenta la presencia
de los dem�s electrones. |
Los dos electrones que se agregan se suponen con
energ�as muy cercanas a la energ�a de Fermi; pero por fuera de la superficie
de Fermi asociada al metal. De este modo, la energ�a del estado base del
nuevo sistema de N+2 part�culas es E0(N)+2EF,
donde E0(N) es la energ�a del estado base del sistema
original de N electrones. |
Se hace la suposici�n de que los dos electrones adicionales
interaccionan a trav�s de un potencial de dos cuerpos V(X1
- X2) y se hace la aproximaci�n de un gas de electrones
libres para el estado inicial del sistema, que es una representaci�n razonable
para el estado normal de un metal. Se impone la condici�n de que los dos
electrones introducidos son tales que han de tener �mpetus lineales de
igual magnitud pero de sentido contrario y que tengan espines opuestos.
La conveniencia de esta condici�n es la siguiente: el estado base del
metal normal tiene �mpetu lineal igual a cero y esp�n igual a cero (para
metales simples) y si no se impusiera esta condici�n el sistema de N
+ 2; part�culas exhibir�a corriente y esp�n netos diferentes de cero.
La interacci�n entre los electrones se toma como atractiva sin averiguar
ni interesarse, por el momento, en el camino que lleve a ella, en c�mo
puede llegarse a dar esta atracci�n entre dos electrones en el material.
|
Para entender mejor el modelo que se escoge para
la interacci�n pasemos al espacio de Fourier, en donde denotaremos la
interacci�n como V(K1 - K2). Consideremos
la esfera de Fermi de radio KF correspondiente a la
energ�a de Fermi EF, como se muestra en la figura 11
y alrededor de esta esfera, un cascar�n esf�rico con un espesor de hwD,
donde h es la constante de Planck dividida entre 2p
y wD es la frecuencia de Debye. N�tese que el espesor del
cascar�n es mucho menor que el radio de la esfera de Fermi en virtud de
las magnitudes de EF y de hwD. El
potencial se escoge de manera tal que V(K1 - K2)
= 0, cuando K1 y K2 est�n fuera del
cascar�n de espesor hwD, y V(K1
- K2) = -V, donde V es una constante
positiva, si K1 y K2 est�n dentro
del cascar�n. N�tese que as�, si K1 y K2
est�n ambas dentro del cascar�n esf�rico, la atracci�n entre los electrones
del par es constante. |
Con este modelo, resolviendo el problema cu�ntico
de la funci�n de onda del par y el problema de valores propios de la energ�a
del par, se encuentra que siempre existe un estado ligado, sin importar
qu� tan d�bil sea la atracci�n entre los electrones, esto es, sin importar
qu� tan peque�a sea la constante V |
| Se encuentra que la energ�a del estado ligado est�
dada por: |
 |
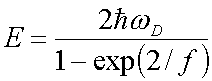| donde f= N(O)V, siendo N(O) la densidad
de estados electr�nicos para el nivel de Fermi. El valor de f puede
ser aproximado como pn x 10-6, donde p es la
resistividad de alta temperatura y n es la densidad electr�nica
del material. El valor t�pico de f resulta de 0.3 y as� vemos que
E resulta ser << hwD.
|
| Es posible obtener, en el espacio f�sico, la separaci�n
promedio de los elementos del par de Cooper. La ra�z cuadr�tica media
del radio de un par, (p2)1/2 se puede calcular
por medio de la f�rmula: |
 |
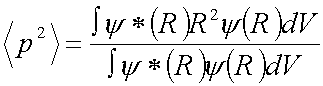donde Y(R) es la
funci�n de onda del par. El resultado final es (p2) = 8h2EF/(3m2E2),
cuyo valor para un metal como el aluminio resulta de 104 angstroms
(o 10-4 cm). N�tese que �sta es una distancia muy grande comparada
con una separaci�n t�pica de electrones en el mismo material que es del
orden de 1 angstrom. |
As� que si suponemos que en un material en estado
superconductor existen pares de Cooper, habr�a entre ellos un traslape
grande e importante. Tenemos tambi�n, como consecuencia de la existencia
de los pares de Cooper y la separaci�n macrosc�pica entre sus elementos,
la posibilidad de efectos macrosc�picos. |
Puede decirse que el resultado m�s importante del
an�lisis de Cooper es que al formar un par con electrones que tienen �mpetus
de igual magnitud pero de signos opuestos, la disminuci�n de la energ�a
potencial debida a la interacci�n supera el aumento en la energ�a cin�tica
que se tiene por arriba de 2EF. Es decir, si los dos
electrones quedan representados por un estado Y
en el cual son dispersados frecuentemente entre estados con �mpetus de
la misma magnitud pero de sentido opuesto, dentro de un intervalo de
Dp= mhwD/PF, la energ�a
total del sistema es menor de lo que ser�a si los electrones estuvieran
en estados infinitesimalmente por arriba de la superficie de Fermi pero
sin atracci�n entre ellos. |
Del resultado obtenido para el par de Cooper tenemos
que en el espacio f�sico (espacio R), tomando en cuenta el problema
de muchos cuerpos, un electr�n con esp�n hacia arriba y vector de onda
k est� correlacionado con todos los electrones de vector de onda
-k y esp�n hacia abajo, en un radio de 104 angstroms.
En el espacio de Fourier (espacio k) est� correlacionado solamente
con otro electr�n. |
Considerando que en un material en el estado superconductor
existen del orden de 1023 electrones y considerando que existen
tambi�n pares de Cooper, uno podr�a preguntarse cu�l es la probabilidad
de encontrar un electr�n con vector de onda -k y esp�n para abajo
en un elemento de volumen dV2 a una distancia r
de un electr�n con vector de onda k y esp�n para arriba contenido
en un elemento de volumen dV<1. |
| En el metal en estado normal la probabilidad es
independiente de r y la respuesta a la pregunta es n2
dV1 dV2 /4. Para el metal
en el estado superconductor y valores muy grandes para la separaci�n r,
la respuesta sigue siendo la misma, pero para otros valores de r,
la probabilidad es mayor, exhibiendo as� el hecho de que es m�s probable
encontrar cercanos entre s� a los electrones apareados que muy separados,
como se muestra en la figura 12. N�tese que si le llamamos al radio del
par de Cooper r0, en un volumen dado por r03
existen del orden de 107 pares, de tal forma que las funciones
de onda se traslapan considerablemente. |
Es interesante hacer notar que el mismo Cooper, en
su artículo del año 1956, donde trata el problema del par
de electrones, menciona que unos años antes, en 1952, V. L. Ginzburg
publicó un trabajo en donde considera un problema semejante al
par que considera Cooper. En palabras del propio Cooper, cuando hace referencia
al trabajo de V. L. Ginzburg de 1952: "También ha sidosugerido
que las propiedades superconductoras pueden resultar si se considera que
los electrones pudieran combinarse en agrupamientos pares de tal manera
que los agregados resultantes obedecen la estadística de Bose."
De este modo podríamos decir que Ginzburg se anticipó en
la idea algo así como cuatro años y medio (el trabajo de
Cooper se publicó en el mes de diciembre de 1956). |
A pesar de que el par de Cooper tiene esp�n total
cero y corresponde a un par de electrones ligados y pudiera en algunos
aspectos seguir la estad�stica de Bose no es, estrictamente hablando,
un bos�n. |
Esto puede entenderse f�cilmente si se recuerda que
el par de Cooper est� constituido por dos electrones ligados entre s�.
De este modo, los elementos del par de Cooper tienen que satisfacer la
estad�stica de Fermi, ya que deben seguir cumpliendo con el principio
de exclusi�n de Pauli. Esto puede entenderse f�cilmente si se recuerda
que el par de Cooper est� constituido por dos electrones ligados entre
s�. De este modo, los elementos del par de Cooper tienen que satisfacer
la estad�stica de Fermi, ya que deben seguir cumpliendo con el principio
de exclusi�n de Pauli. |
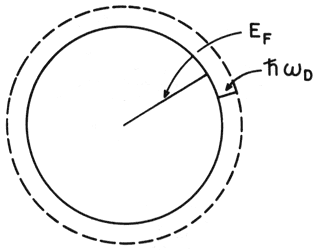
Figura 11. Representaci�n, en el espacio de Fourier, del problema del par de cooper.
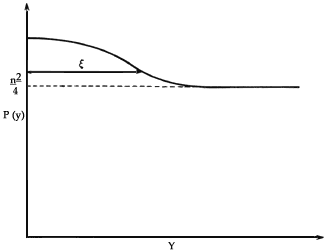
Figura 12. Probabilidad P(r) dV 1 dV 2
de encontrar a un electr�n con vector de onda -k y esp�n para abajo en
un volumen dV2 a una distancia r de un volumen dV
1 que contiene a un electr�n con vector de onda k y esp�n
para arriba. Para el metal en el estado normal es n2/4, donde
n es la densidad electr�nica cl�sica. Para el estado superconductor la
probabilidad es mayor, como puede verse en la gr�fica, dentro de un intervalo
E ~ 10-4 cm.
El mecanismo que brevemente hemos expuesto para tener la posibilidad de una atracci�n entre dos electrones es el que se tiene en los superconductores convencionales. Para los nuevos materiales superconductores cer�micos no se sabe con certeza el mecanismo que lleva a la formaci�n de los pares de Cooper. Se tiene ya evidencia de que, al menos en parte, los fonones contribuyen a la formaci�n de los pares de Cooper. Esto es por la presencia de un d�bil efecto isot�pico. Tambi�n es claro ya que los fonones no son los �nicos posibles responsables de la formaci�n de los pares de Cooper y que todo parece indicar que hay varias contribuciones para la formaci�n de �stos. Para los materiales cer�micos superconductores no existe a�n una teor�a satisfactoria acerca del origen de la superconductividad en ellos. Aunque hay varias propuestas, la controversia no est� resuelta.
En 1957, J. Bardeen, L. Cooper, y R. Schrieffer, utilizando la idea del par
de Cooper, se abocaron a la tarea de resolver el problema te�rico desde el punto
de vista de la mec�nica cu�ntica, de la superconductividad en un metal. Supusieron
que la interacci�n atractiva entre dos electrones era por medio de los iones
del metal. Tuvieron un �xito rotundo para explicar el fen�meno, especialmente
en lo que se refiere a los resultados experimentales de los superconductores
ahora conocidos como de Tipo I. Por su teor�a, ahora conocida como teor�a BCS,
Bardeen, Cooper y Schrieffer recibieron el premio Nobel de F�sica en 1972.
Actualmente se piensa que todos los metales, que son buenos conductores de electricidad, pueden en principio convertirse en superconductores a temperaturas suficientemente bajas.
En la siguiente secci�n veremos c�mo la forma de la muestra de material afecta la presencia de la superconductividad; c�mo la geometr�a de la muestra afecta al estado superconductor, lleg�ndose a lo que se conoce como el estado intermedio.
En electromagnetismo es conocido el fen�meno de la desmagnetizaci�n, debido
al cual la intensidad de campo magn�tico, H, en el interior de un cuerpo
es un campo desmagnetizante. La forma en que este campo magn�tico se distribuye
depende, en general, de la geometr�a de la muestra. Para una muestra que es
un elipsoide de revoluci�n, con un campo magn�tico aplicado, Ha,
paralelo al eje de revoluci�n de la muestra (figura 13), es posible demostrar
que el campo interno es uniforme y paralelo al campo aplicado y que est� dado
por: Hint = Ha - nM, donde M
es la magnetizaci�n y n es un factor conocido como factor de desmagnetizaci�n
y que depende de la geometr�a del cuerpo.
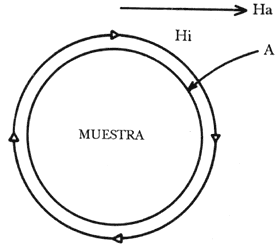
Figura 13. Muestra cil�ndrica en el seno de un campo magn�tico perpendicular
al eje del cilindro. En el interior del cilindro el campo magn�tico es mayor
que fuera de �l, por el factor de desmagnetizaci�n.
Para un elipsoide alargado, n = (1/e - 1)[(1/2e)ln((1 + e)/ (1 - e)) - 1], donde e es la excentricidad del elipsoide. Para una esfera, n = 1/3; para un cilindro circular recto con su eje perpendicular al campo magn�tico aplicado n = 1/2 y para el mismo cilindro, pero con su eje paralelo al campo aplicado, n = 0.
Para el caso de un superconductor: M = - Hint y as�:
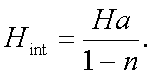
De este modo tendremos que el campo magn�tico en el interior de la muestra va a ser m�s intenso que en su superficie exterior y as�, antes de que el campo aplicado externamente llegue al valor del campo cr�tico de la muestra tendremos que, en su interior, el valor del campo cr�tico ya ha sido alcanzado. Al imponer las condiciones de frontera que debe satisfacer el campo H (condiciones de frontera entre las regiones en estado normal y las regiones en el estado superconductor), se deduce que no existe una superficie con fronteras simples para la que se puedan satisfacer las condiciones para el campo H.
El problema puede resolverse notando que las fases normal y superconductora pueden existir una al lado de la otra en equilibrio, de la misma manera que un l�quido puede coexistir con su vapor si la presi�n es igual a la presi�n del vapor de saturaci�n. Una posible configuraci�n podr�a constar, por ejemplo, de zonas cil�ndricas, delgadas, en estado normal, coexistiendo con la regi�n superconductora. Algunas l�neas del campo magn�tico podr�an penetrar la muestra por las regiones en estado normal.
Es posible demostrar que la energ�a libre del sistema, para una configuraci�n como la mencionada, es menor que la correspondiente cuando toda la muestra se encuentre en el estado normal. Tambi�n es posible demostrar que es menor que si toda la muestra se encuentra en el estado superconductor.
Al estado de una muestra en el que coexisten fases normales con fases superconductoras,
por efectos estrictamente de la geometr�a de la muestra, se le denomina estado
intermedio. Existe evidencia experimental de la existencia del estado intermedio
gracias al trabajo de muchos investigadores. Dos de los primeros que informaron
sobre la existencia del estado intermedio fueron Shalnikov y Meskovsky, quienes,
en 1945, 1947 y 1949, realizaron experimentos muy interesantes al respecto.
Lo que hicieron esencialmente en sus experimentos fue explorar la presencia
del campo magn�tico en una peque�a separaci�n entre dos hemisferios de esta�o
superconductor de un di�metro de unos 4 cm. La exploraci�n del campo magn�tico
entre los dos hemisferios se hizo utilizando un alambre de bismuto muy peque�o.
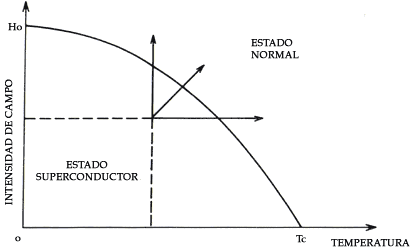
Figura 14. Diagrama de fases de un material superconductor Tipo I, en t�rminos
del campo magn�tico aplicado y la temperatura. Las regiones que quedan fuera
del cuadro que corresponde al estado superconductor, pero que quedan fuera de
la zona del estado normal, corresponden al estado intermedio.
Se utiliz� bismuto para aprovechar su resistividad, que es muy sensible a la
presencia de un campo magn�tico. Por medio de la sonda de bismuto, se midi�
el valor del campo magn�tico adyacente a ella, el cual resultaba cero en la
vecindad de regiones superconductoras y era igual, a moHc,
en las regiones normales. Desde luego que la distribuci�n de regiones normales
y superconductoras result� mucho m�s complicada que la estructura que aqu� se
ha sugerido, pero lo m�s importante es que se demostr� muy claramente la coexistencia
de fases normales y superconductoras, esto es, la existencia del estado intermedio
(figura 15).
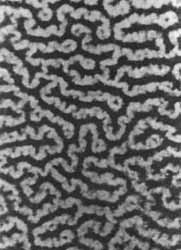
Figura 15. Fotograf�a que muestra la existencia del estado intermedio en
un superconductor Tipo I. Las partes oscuras son las superconductoras y las
claras son las que se encuentran ya en estado normal.
Otros m�todos para la observaci�n del estado intermedio se basan en la tendencia de las part�culas de material ferromagn�tico a acumularse en regiones de alta intensidad de campo magn�tico y de part�culas de material superconductor (que es un diamagneto perfecto) a acumularse en regiones de baja intensidad de campo magn�tico.
Fue en 1935 cuando Eugene Wigner (premio Nobel de F�sica en 1963 por sus contribuciones al estudio del n�cleo at�mico y las part�culas elementales), y Helen Huntington predijeron que el hidr�geno podr�a llegar a una fase met�lica si se le aplicaba una presi�n hidrost�tica suficientemente alta. Desde entonces se ha intentado su obtenci�n en el laboratorio para el estudio de sus propiedades.
En 1968 N. W. Ashcroft sugiri� por vez primera que el hidr�geno met�lico podr�a ser un material superconductor. Se interes� en este material al notar que J�piter, planeta que est� compuesto principalmente de hidr�geno, presentaba un campo magn�tico an�malamente intenso. A saber que las presiones en el interior de J�piter eran enormes (del orden de millones de atm�sferas), hizo la conjetura de que quiz� el hidr�geno se encontraba all� en estado met�lico. Con esta suposici�n y tomando el valor de algunos par�metros del hidr�geno en estado met�lico, hizo una estimaci�n del valor de la posible temperatura de transici�n superconductora. Obtuvo un valor, de alrededor de 100 Kelvin, que es una temperatura comparable a la existente en el interior de J�piter. As� sugiri� Ashcroft que el campo magn�tico de ese planeta podr�a deberse a que el hidr�geno que lo compone se halla en estado superconductor.
Pero hab�a que hacer c�lculos mucho m�s serios y detallados antes de afirmarlo con toda certeza. C�lculos posteriores, sumamente detallados y precisos realizados en M�xico (en el Instituto de F�sica de la UNAM) llevan a valores de una temperatura de transici�n para el hidr�geno met�lico de alrededor de 300 Kelvin, reforz�ndose as� la sugerencia hecha por Ashcroft. Los c�lculos sobre la densidad del hidr�geno en J�piter var�an de 0.l gr/cm3, en la superficie a 5 gr/cm3 cerca del centro, lo que indica que el hidr�geno bien puede estar en estado s�lido y que, adem�s, pudiera ser met�lico.
En el laboratorio, el hidr�geno met�lico es dif�cil de obtener. Sin embargo,
en 1972 un grupo de cient�ficos sovi�ticos (Grigorev y colaboradores) lo obtuvo
por vez primera. Tambi�n en la URSS, en 1975, Vereshchagen y colaboradores lo
obtuvieron nuevamente. Utilizaron una t�cnica de implosi�n de dos cilindros
conc�ntricos para alcanzar las elevadas presiones que se requieren y observaron
un cambio brusco en el valor de la conductividad el�ctrica del hidr�geno. Desde
luego que solamente se mantuvo por unas fracciones de segundo, insuficientes
para detectar las propiedades de este material.
En Jap�n tambi�n, en 1980, se inform� sobre la obtenci�n de hidr�geno met�lico con una t�cnica muy distinta, en la que las altas presiones se obten�an por medio de presiones ejercidas con un tornillo. Pero parece que este experimento no ha sido reproducible. Posteriormente se pudo obtener hidr�geno cristalino, pero sin llegar a establecer si era met�lico, ejerciendo presi�n sobre el material por medio de yunques de diamante, a presiones de 2.5 millones de atm�sferas. Esto fue a mediados del decenio 1980-1990. En marzo de 1996 se obtuvo hidr�geno met�lico a partir de hidr�geno fluido utilizando un ca��n de dos etapas para crear una onda de choque de enorme presi�n sobre un blanco que conten�a hidr�geno l�quido enfriado a 20 K. El experimento fue realizado en el Laboratorio Nacional Lawrence Livermore, de Estados Unidos. La presi�n requerida fue de 1.4 millones de atm�sferas. El estado met�lico del hidr�geno no dur� lo suficiente como para determinar si se encontraba en el estado superconductor.
La posibilidad de obtener un superconductor de alta temperatura cr�tica ha sido muy atractiva desde el momento en que se descubri� la superconductividad. Los beneficios tecnol�gicos que se obtendr�an son muy claros y nos referiremos a ellos en el �ltimo cap�tulo. Se ha desplegado un enorme esfuerzo, tanto te�rico como experimental, hacia la consecuci�n de un material superconductor de alta temperatura cr�tica, y no fue sino hasta 1987 cuando, con una clase totalmente nueva de materiales superconductores, los superconductores cer�micos, se lograron temperaturas del orden de 100 Kelvin. El manejo tecnol�gico de los materiales cer�micos es bastante problem�tico, pero no es imposible.
Los superconductores cer�micos pertenecen a la clase conductores denominados Tipo II o superconductores duros. Presentan elevados valores para el campo magn�tico cr�tico. En el siguiente cap�tulo nos ocuparemos de las principales caracter�sticas de los superconductores Tipo II.
