V. ESTRUCTURA INTERNA DE LA TIERRA
EN EL cap�tulo anterior nos preguntamos qu� tan antigua es la Tierra, y al tratar de responder esta pregunta nos dimos cuenta que est� directamente relacionada con la del origen del Sistema Solar. Sabemos ahora que los meteoritos, la Luna y otros planetas tienen la misma edad que la Tierra. Este hecho viene a sumarse a otras evidencias que nos permiten decir con seguridad que los miembros del Sistema Solar tuvieron un mismo origen.
En realidad, esta conclusi�n ya era compartida por los astr�nomos mucho tiempo antes, pues se hab�a logrado precisar que los planetas tienen ciertas caracter�sticas que se�alan un origen com�n. En primer lugar, casi todos los planetas tienen �rbitas regulares, casi circulares y coplanares. Por otro lado, se trasladan en la misma direcci�n (al rev�s de las manecillas del reloj si los observamos desde la Estrella Polar) y con excepci�n de Venus y Urano, los dem�s planetas del sistema tienen el mismo sentido de rotaci�n que la Tierra. Finalmente, las distancias de los planetas al Sol no son arbitrarias y parecen seguir un orden regular.
Esta regularidad se conoce como ley de Bode y se expresa como:
donde dn es la distancia desde cada uno de los planetas al Sol (en unidades
astron�micas, esto es: 1 U.A. = distancia promedio del Sol a la Tierra) y n
un n�mero asignado a cada planeta. De esta manera, n = -
,
es para Mercurio, n = 0 para Venus, n = 1 para Marte, y as� sucesivamente. Esta
f�rmula describe de manera admirable las distancias determinadas astron�micamente
(excepto para Neptuno y Plut�n), y es interesante notar que predice la existencia
de un planeta a 2.8 U.A., que es precisamente la distancia promedio de los asteroides
al Sol. De hecho, este resultado permiti� su posterior descubrimiento. No se
ha podido explicar te�ricamente la ley de Bode, pero seguramente est� relacionada
con la din�mica de formaci�n del Sistema Solar.
Los factores antes mencionados sugieren un origen com�n para el Sistema Solar. En el presente siglo los astr�nomos pudieron observar que los procesos de nucleos�ntesis, en efecto, se realizan en el interior de las estrellas, y esto ha permitido formar modelos de creaci�n del Sistema Solar a partir de nebulosas c�smicas.
Varios modelos han sido propuestos pero todos ellos incluyen la formaci�n de los elementos en el seno de lo que luego ser�a el Sol y la posterior formaci�n y acrecentamiento de los planetas. Probablemente, en una primera etapa los planetas interiores o terrestres (Mercurio, Venus, Tierra y Marte) fueron despose�dos de una gran porci�n de sus elementos m�s ligeros por efecto del viento solar y quedaron relativamente enriquecidos de elementos pesados. Los elementos m�s comunes actualmente en la corteza terrestre son los siguientes:
UADRO 5. Abundancia promedio de los elementos en las rocas de la
corteza terrestre seg�n Clarke y Washington (1924).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FUENTE: Garland, 1971. |
|
Este cuadro nos muestra que el ox�geno y el silicio son los elementos m�s abundantes. Naturalmente �stos son resultados del an�lisis de rocas superficiales y uno se pregunta con justicia si la misma composici�n se encuentra en el interior de la Tierra. Un indicio de que esto no es as� nos lo dan de nuevo los meteoritos, pues como hemos visto, se presentan en dos variedades muy diferentes desde el punto de vista qu�mico: los l�ticos, es decir, los de composici�n rocosa, y los met�licos.
Una segunda evidencia nos la proporciona la densidad media de los planetas y la Luna que se presenta en el cuadro 6.
En este cuadro se ve que la Tierra tiene una densidad media mayor que la de las rocas superficiales m�s densas (la densidad media de �stas es de alrededor de 2.5 gr/cm3). Esto indica que la Tierra (y ya se ha demostrado por otros m�todos como veremos despu�s) posee un n�cleo interno de mayor densidad que el resto. Posiblemente Mercurio, Venus y Plut�n tambi�n posean n�cleos m�s densos que el resto de su materia. Por lo que respecta a la Luna, la densidad media de las rocas lunares es de 3.3 gr/cm3; esto sugiere que la variaci�n radial en su densidad es peque�a.
UADRO 6. Densidad media de los planetas
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
FUENTE: Garland, 1971. |
||
Otras evidencias adicionales son proporcionadas indirectamente por otros fen�menos como las mareas terrestres. Éstas consisten en una deformaci�n de la parte s�lida de la Tierra debida a la atracci�n gravitacional de la Luna y el Sol, que causa tambi�n las mareas oce�nicas. Si se supone que la Tierra es homog�nea y se calculan las deformaciones que tendr�a por efecto de la atracci�n luni-solar se obtienen valores que no concuerdan con los observados, lo cual sugiere que el planeta tiene una estratificaci�n interna.
Otra evidencia fuerte de la estratificaci�n interna de la Tierra nos la proporciona su momento de inercia. El momento de inercia es el equivalente de la masa en el caso de un movimiento circular. En efecto, en el movimiento rectilíneo, la aceleraci�n que adquiere un cuerpo cuando se le aplica una fuerza depende de su masa; de la misma manera, cuando un cuerpo es puesto en rotaci�n su aceleraci�n angular (es decir, el cambio en el n�mero de revoluciones que da por unidad de tiempo) depende de su momento de inercia. Para un cuerpo en rotaci�n �ste es la suma del producto de inercia de cada una de las part�culas que componen el cuerpo. A su vez, para cada part�cula de masa m el momento de inercia es:
donde r es la distancia de la part�cula al eje de rotaci�n, de manera que observamos que la velocidad angular depende no s�lo de la masa sino de la manera que las part�culas est�n distribuidas con respecto al eje de rotaci�n. Ésta es la raz�n por la cual los trompos poseen esa forma caracter�stica que les da un mayor momento de inercia que a su vez les permite vencer la fuerza de fricci�n contra el piso.
La Tierra tiene tambi�n un momento de inercia con respecto a su eje de rotaci�n. Éste ha sido determinado a trav�s de medidas de la gravedad y del movimiento de precesi�n de la Tierra causado por la atracci�n luni-solar. El momento de inercia determinado de esta manera es 0.331 mr2, donde m es la masa de la Tierra y r su radio. Sin embargo, para una esfera homog�nea el momento de inercia es 0.4 mr2. La diferencia se debe al hecho de que en la Tierra hay una concentraci�n de material m�s denso cerca del eje de rotaci�n, esto es, el n�cleo interno.
Sin embargo, la informaci�n m�s completa sobre la existencia de una estratificaci�n interna del planeta es proporcionada por la sismolog�a. Los sismos, esos movimientos de tierra cuyos efectos son la causa de innumerables p�rdidas de vidas, tienen al menos la propiedad de proporcionarnos informaci�n sobre el interior de la Tierra.
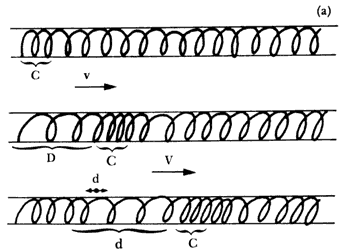
Veamos esto un poco m�s detalladamente. Cuando arrojamos una piedra en un estanque notamos que en el seno del l�quido se producen ondas. Éstas son energ�a que se propaga radialmente. El l�quido sufre un movimiento oscilatorio, sin embargo, no es el l�quido lo que se mueve sino la perturbaci�n que se comunica de part�cula en part�cula de la misma manera que las ondas producidas en una cuerda. En un s�lido tambi�n se pueden propagar ondas, s�lo que, a diferencia de los l�quidos, se pueden propagar dos tipos de ondas. Unas de �stas son las llamadas ondas longitudinales, en las cuales las part�culas vibran en la misma direcci�n en que viaja la onda. En el segundo tipo, el de las llamadas ondas transversales, las part�culas vibran en direcci�n perpendicular a la direcci�n de propagacion de la onda (Figura 12). Las velocidades de ambos tipos de onda son diferentes. Las ondas longitudinales se propagan a mayor velocidad que las transversales y por este motivo son conocidas como ondas P (Primus), pues su llegada a un sitio dado se registra primero que la de las ondas transversales, que son por ello conocidas como ondas S (Secundus). No entraremos en los detalles de c�mo se generan los temblores; sin embargo, podemos decir brevemente que un temblor es el resultado de un fallamiento, ruptura o dislocaci�n de las rocas m�s superficiales de la Tierra (los sismos m�s profundos ocurren a unos 700 km bajo la superficie). La fricci�n entre ambas caras de la falla permite acumular energ�a el�stica que, cuando es liberada durante la ruptura, genera ondas s�smicas. Una analog�a de este comportamiento lo encontramos en las ondas sonoras que se producen en el contacto entre el piso y un objeto pesado cuando lo arrastramos y que percibimos como un ruido caracter�stico.
Al igual que una l�mpara emite ondas luminosas, el �rea cuya ruptura ocasiona un sismo se comporta como un foco emisor de ondas P y S. Las ondas s�smicas se comportan de manera an�loga a las ondas luminosas pues son fen�menos del mismo tipo.
 |
 |
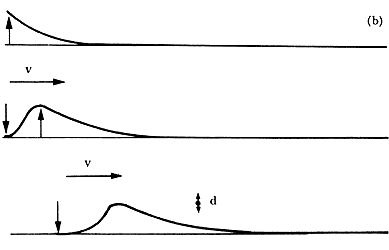Figura 12. Las ondas internas P y S se propagan por vibraciones de las part�culas. En el caso de las ondas P el movimiento de �stas se da en la misma direcci�n en que se propaga la onda. Para las ondas S el movimiento de las part�culas es transversal.
Sabemos que las ondas luminosas sufren reflexiones y refracciones cuando inciden en un medio con diferentes propiedades; este mismo efecto se observa en las ondas s�smicas. Si representamos por rayos la propagaci�n de las ondas luminosas, los fen�menos de reflexi�n y refracci�n ocurren como se ilustra en la figura 13(a).
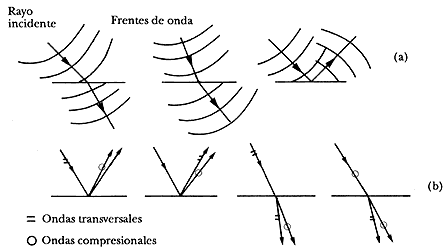
Figura 13. (a) Refracci�n y reflexi�n de un rayo de luz; (b) reflexi�n y refracci�n de ondas s�smicas.
En el caso de las ondas s�smicas el fen�meno es un poco m�s complicado puesto que la incidencia de ondas P y S produce ondas P y S refractadas y reflejadas. La figura 13 (b) muestra c�mo sucede el fen�meno en los rayos s�smicos.
Cuando la velocidad en el medio en el que incide un rayo es mayor que la del medio en que viaja, el rayo se aparta de la perpendicular, y viceversa; cuando la velocidad es menor se aproxima a �sta. Por tal raz�n las ondas P y S refractadas no siguen trayectorias iguales puesto que en un medio dado ambas ondas poseen diferentes velocidades.
En la Tierra la rigidez, y con ello la velocidad, aumentan continuamente hacia su interior, de manera que el efecto de refracci�n hace que los rayos sigan trayectorias curvas (Figura 14).
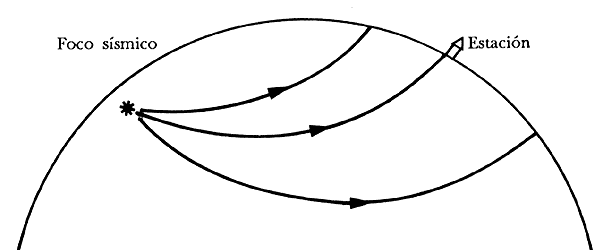
Figura 14. Trayectoria de las ondas s�smicas en el interior de la Tierra.
Si el terremoto es lo suficientemente fuerte, las ondas s�smicas pueden propagarse con suficiente intensidad para ser registradas en estaciones sismol�gicas alrededor del mundo. En este punto es necesario hacer una peque�a pausa para hablar de los sismogramas y los sism�grafos, que son los instrumentos esenciales de la sismolog�a.
Puesto que los terremotos consisten en la propagaci�n de las ondas s�smicas a trav�s de la Tierra, nos interesa registrar su paso en un punto dado de la superficie del planeta, esto es, nos interesa conocer el movimiento del terreno en un punto dado. Una forma ideal de construir un sism�grafo ser�a el suspender un estilete del vac�o y registrar el movimiento del suelo por medio de un tambor sujeto al suelo y que gira con velocidad constante (Figura l5a).
En este sism�grafo ideal el estilete se encuentra suspendido en el vac�o, puesto que suspendido de un soporte r�gido sobre la Tierra se mover�a junto con �sta y no inscribir�a el movimiento del suelo sobre el tambor.
Ahora bien, no es posible suspender un estilete o marcador del vac�o, pero podemos resolver el problema si sujetamos el estilete de una masa de tama�o apropiado, pues como sabemos por la primera ley de Newton, una masa tiende a permanecer en su estado de reposo si no hay una fuerza que la acelere. De esta manera, el movimiento del suelo puede registrarse debido a la inercia de la masa en que est� colocado el estilete. Adem�s de la masa, nuestro sism�grafo debe ser complementado con un sistema de amortiguamiento que evite la oscilaci�n libre de la masa. En nuestro diagrama de la figura 15(b) aparece un sistema bastante simple. Con �l ser�a imposible obtener registros �tiles puesto que el movimiento del suelo aparecer�a apenas perceptible si el sismo es lejano o peque�o. Por esta raz�n, los sism�grafos reales necesitan un sistema que amplifique el movimiento del suelo. En los primeros sism�grafos el sistema de amplificaci�n era mec�nico y en general se requer�an masas bastante grandes para vencer las fuerzas de fricci�n y obtener sismogramas �tiles. En la estaci�n de Tacubaya en la ciudad de M�xico existe en operaci�n un sism�grafo tipo Wiechert cuya masa es de 17 toneladas. En la actualidad los sistemas amplificadores son electr�nicos y se requieren masas de algunos cientos de gramos o algunos kilogramos, seg�n el uso que se intente dar al instrumento.
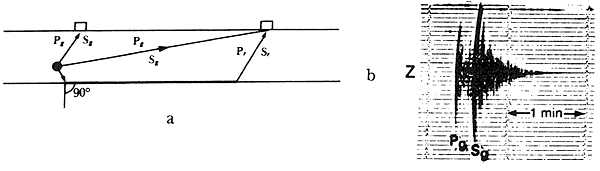
Como el movimiento del terreno ocurre en tres dimensiones, es decir, las part�culas del suelo se pueden mover en cualquier direcci�n horizontal y vertical, una estaci�n sismol�gica completa consta de seis sism�grafos que se orientan por convenci�n y comodidad en las direcciones este-oeste, norte-sur y vertical. Tres de esos instrumentos son m�s sensibles a las vibraciones con periodos cortos y los otros tres a los de periodo largo. Los registros que se obtienen con un sism�grafo son llamados sismogramas; la figura 16 nos ilustra sismogramas t�picos de un sismo lejano y uno cercano.
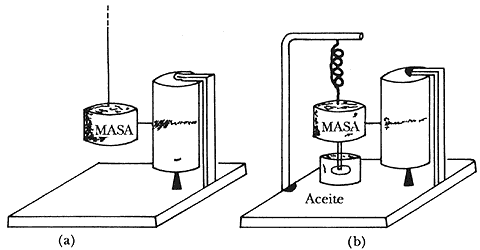
Figura 15. Esquema de un sism�grafo vertical.
Retomando el tema inicial de este cap�tulo, hemos referido que la velocidad de las ondas aumenta progresivamente hacia el interior del planeta. Esto se cumple hasta cierta profundidad. En 1906 R. D. Oldham not� que en las ant�podas de un foco s�smico las ondas P llegaban con retraso en comparaci�n con el tiempo de llegada esperado si la velocidad aumentara gradualmente hasta el centro del planeta. Oldham, para explicar este fen�meno, plante� la existencia de un n�cleo en que las velocidades s�smicas son menores. En 1912 Beno Gutemberg verific� la existencia de una "zona de sombra" entre los 105 y 143 grados, es decir, una zona en que las ondas P no llegaban con las amplitudes y tiempos esperados. Con base en esta observaci�n, Gutemberg calcul� la profundidad de dicho n�cleo en 2 900 km, una cantidad que las determinaciones m�s modernas no han corregido sino en unos cuantos kil�metros.
La parte de la Tierra que cubre al n�cleo fue designada con el nombre alem�n de "mantel" por Wiechert, de donde derivaron los t�rminos mantle en ingl�s y manto en espa�ol.
|
|
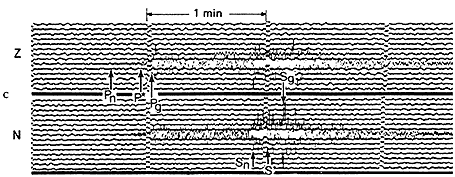
Figura 16. Sismogramas t�picos de b) un sismo cercano y c) un sismo lejano.
La "sombra" arrojada por el n�cleo no es total, ya que se observan ondas P de peque�a amplitud en esta zona. Durante alg�n tiempo se trat� de explicar esta presencia por efecto de difracci�n en el n�cleo; sin embargo, en 1936, Ilse Lehman, sism�loga alemana, sugiri� que estas ondas eran debidas a la existencia de un n�cleo interno de alta velocidad. La profundidad del n�cleo interno result� ser de 5 120 km y luego de que en 1939 H. Jeffreys, un geof�sico brit�nico pionero de la sismolog�a, demostr� que las ondas que aparec�an en la zona de sombra no pod�an ser ocasionadas por difracci�n, su existencia fue ampliamente reconocida y verificada. Para distinguir entre ambas partes del n�cleo, se llama n�cleo externo a la regi�n que cubre al n�cleo interno.
Una caracter�stica adicional del n�cleo externo es su incapacidad de transmitir ondas S. Este comportamiento es t�pico de los l�quidos. Suponga el lector que coloca una l�mina s�lida en el interior de un l�quido y le da un impulso paralelo a la superficie de la l�mina; con tal movimiento le ser� imposible crear una perturbaci�n que se propague en el seno del mismo. Si, por el contrario, el movimiento es en direcci�n perpendicular a la cara de la l�mina, se generar� una perturbaci�n u onda que se propaga en la misma direcci�n. Esta �ltima es una onda P. As� pues, como el n�cleo externo es incapaz de transmitir estas ondas, se dice que se encuentra en estado l�quido.
Hemos dicho que la parte externa de la Tierra es llamada manto, sin embargo, podemos preguntarnos si �ste es continuo hasta la superficie de nuestro planeta o por el contrario existe una discontinuidad entre la parte superior y el manto. La respuesta fue dada en 1909 por A. Mohorovicic, sism�logo croata, quien demostr� que la parte m�s superficial del planeta, ahora llamada corteza terrestre, posee velocidades s�smicas menores que las del manto y est� separada de �ste por una discontinuidad que en su honor lleva su nombre: discontinuidad de Mohorovicic o simplemente Moho.
La discontinuidad no se encuentra a una misma profundidad en toda la Tierra, y var�a considerablemente de un lugar a otro; en los continentes su espesor t�pico es de 30 a 40 km y en los oc�anos de l0 a l5 km.
Con el transcurso del tiempo ha aumentado el caudal de datos sismol�gicos y �stos han aportado informaci�n m�s detallada sobre el interior del planeta. En la actualidad se sabe que en el manto existen zonas de discontinuidad caracterizadas por bajas velocidades s�smicas. Asimismo, se ha podido reconocer que algunas discontinuidades como la que existe entre el n�cleo exterior y el interior, no son abruptas sino difusas y complejas. La figura 17(a) muestra esquem�ticamente la estructura interna de la Tierra y la figura 17(b) las velocidades s�smicas en su interior, obtenidas de los datos sismol�gicos.
Podemos observar que entre los 400 y 1 050 km se marcan zonas de disminuciones abruptas de velocidad. Esta regi�n se considera como una zona de transici�n entre lo que se conoce modernamente como manto superior y manto inferior.
