VII. LA CORTEZA TERRESTRE
EN LA secci�n anterior viajamos desde la superficie de la Tierra hasta su n�cleo sin examinar con mayor detalle su corteza. �sta, en cuya superficie se desarrolla la vida, es extraordinariamente interesante tanto por su complejidad como por las preguntas que puede uno hacerse sobre su origen. En efecto, �por qu� tiene una corteza la Tierra?, �cu�l es su estructura, composici�n y edad?
A todas estas preguntas trata de contestar la geolog�a con el auxilio de dos ciencias complementarias: la geof�sica y la geoqu�mica. Es conveniente referirnos, aunque sea brevemente, a los m�todos de la geof�sica, ya que estos constituyen uno de los principales m�todos para conocer la estructura interna de la corteza. Tres m�todos principales son utilizados por la geof�sica para conocer la estructura cortical: el s�smico, el gravim�trico y el magnetom�trico. Estos m�todos no son los �nicos pero si los m�s ampliamente utilizados por lo que, en favor de la brevedad, s�lo nos referiremos a ellos.
M�TODOS GEOF�SICOS PARA EL ESTUDIO DE LA CORTEZA
Hemos hablado ya de c�mo la sismolog�a nos permite conocer indirectamente el interior de un cuerpo s�lido. En esta secci�n hablaremos un poco m�s del mismo tema.
Ya hab�amos visto que una onda que incide sobre una superficie en que las ondas tienen mayor velocidad es refractada hacia el exterior. Notemos que si el �ngulo con que la onda incide va creciendo el rayo refractado se va acercando a la frontera entre los dos medios. Existe un �ngulo en el que el rayo viaja paralelo a la frontera y aparentemente a lo largo de ella (Figura 24).
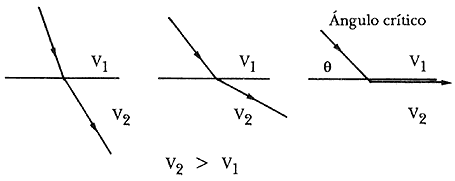
Figura 24. Refracci�n cr�tica en la frontera entre dos medios en la que el inferior tiene mayor velocidad.
Al rayo que viaja en esa direcci�n se le llama rayo cr�ticamente refractado y viaja con la velocidad del medio inferior. En este punto es preciso aclarar que la representaci�n de la onda por medio de un rayo es deficiente para explicar este fen�meno, puesto que, adem�s de otras limitaciones no explica por qu� el rayo viaja con la velocidad del medio inferior, sin embargo, como medio de visualizaci�n es �til y lo seguiremos utilizando. Utilizaremos adem�s un principio muy pr�ctico debido a Fermat y que establece que "en un frente de onda cada punto act�a como una nueva fuente de ondas". De esta manera, cada punto de la frontera entre los medios act�a como emisor de rayos y si tenemos sism�metros en la superficie podemos detectar su arribo a la misma (Figura 25).
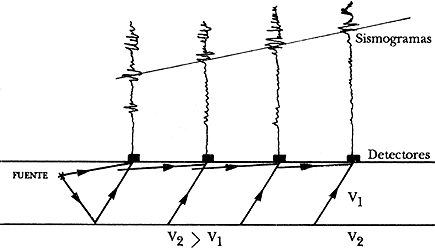
Figura 25. Ilustraci�n del m�todo de refracci�n s�smica.
Notemos que la llegada de las ondas se va retardando progresivamente mientras nos alejamos de la fuente, puesto que deben recorrer distancias m�s grandes. Bas�ndose en este efecto, los sism�logos pueden deducir la profundidad a que se encuentran las fronteras entre estratos y las velocidades de las ondas en los mismos. Este m�todo, conocido como sismolog�a de refracci�n, es de gran utilidad para estudiar la corteza terrestre. La fuente de ondas s�smicas es por lo general una explosi�n con la potencia necesaria para que el equipo detecte las ondas emitidas por ella misma.
Otro m�todo utilizado a menudo es el llamado de "dispersi�n de ondas superficiales". En este m�todo se utilizan las ondas superficiales que emite un temblor natural. Cuando �ste ocurre, como hemos visto, se generan ondas internas P y S. Adem�s de �stas se produce un tipo de ondas de mayor amplitud que se generan y viajan en la superficie del planeta y son conocidas como ondas superficiales. Estas ondas se asemejan a las olas producidas en la superficie de un l�quido, pues su amplitud m�xima la tienen en la superficie y decaen r�pidamente con la profundidad. Las caracter�sticas de las ondas superficiales hacen que �stas viajen por amplias regiones de la corteza y recojan informaci�n sobre la misma. Los sism�logos analizan los registros de estas ondas y pueden deducir la estructura de la corteza por la que se han propagado.
El m�todo gravim�trico es otra forma muy importante de determinar la estructura interna de nuestra corteza. Este m�todo se basa en la atracci�n gravitacional entre masas. Veamos con mayor detalle el fundamento de este m�todo.
Sabemos que dos cuerpos de masas ml y m2 sufren una atracci�n entre s� que est� dada por la f�rmula siguiente:
en esta f�rmula, r es la distancia que separa los centros de masa de los cuerpos y G una constante llamada constante de gravitaci�n universal. Fue el gran Newton quien descubri� esta relaci�n, cuya mejor demostraci�n est� dada por la atracci�n que la Tierra ejerce sobre los cuerpos que se mueven en su superficie. El valor de la constante fue hallado experimentalmente por H. Cavendish, un f�sico ingl�s en 1798. Un valor m�s moderno de la misma es:
G = 6.673x10 cm gr/seg
Ahora bien, la gravedad que nosotros experimentamos sobre la superficie de la Tierra no es exactamente la que corresponde a este valor, porque nuestro planeta se encuentra en rotaci�n. Fue el mismo Newton quien en su famoso libro Principia expuso este hecho. Como podemos ver en la figura 26, todo cuerpo en la superficie del planeta experimenta dos fuerzas: una de ellas es la atracci�n gravitacional del planeta y otra la fuerza centr�fuga debida a la rotaci�n del mismo.
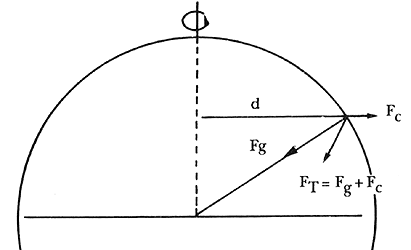
Figura 26. Un objeto sobre la superficie de la Tierra experimenta la atracci�n de la gravedad disminuida por la fuerza centr�peta utilizada en mantener el objeto en rotaci�n; desde el punto de vista del observador en la Tierra, tambi�n se puede pensar que la gravedad experimentada es la suma de la fuerza de gravedad y una "fuerza" centr�fuga.
En un sentido estricto, la �nica fuerza real es la de gravitaci�n. Esta fuerza es la que hace que los cuerpos sigan trayectorias circulares puesto que de otra forma seguir�an trayectorias rectil�neas. Podemos entonces pensar en la situaci�n de dos maneras: una es la que se ilustra en la figura 26 y otra la que tiene m�s sentido f�sico, considerando que no experimentamos toda la fuerza gravitacional porque parte de ella se emplea en mantener una trayectoria circular. La �nica raz�n por la cual se habla de una fuerza centr�fuga es porque muchas veces ignoramos el hecho de que nos encontramos en un sistema en rotaci�n. En otras palabras, la fuerza centr�fuga se introduce como un truco para hablar de un cuerpo que se mueve en trayectoria circular como si estuviera en reposo o en movimiento rectil�neo y con velocidad uniforme.
Volviendo a la consideraci�n sobre la atracci�n gravitacional, la fuerza que debe ejercerse sobre un cuerpo para mantenerlo en una trayectoria circular de radio d est� dada por:
f = mv2 / d
donde d es la distancia entre el objeto y el eje de rotaci�n, y v la velocidad tangencial del objeto debido a la rotaci�n.
Esta fuerza, llamada fuerza centr�peta, es la que debe ser restada de la fuerza de gravedad para obtener la atracci�n neta sobre los cuerpos en su superficie.
Todos los puntos de la Tierra giran 360 grados en 24 horas, de manera que los puntos m�s cecanos al eje de rotaci�n tienen una menor velocidad tangencial, y aunque la distancia d es m�s grande en el ecuador, como la velocidad contribuye al cuadrado resulta que la contribuci�n m�s grande de la fuerza centr�peta se realiza en el ecuador. As�, la gravedad experimentada por un cuerpo es mayor en el polo que en el ecuador; este efecto se refuerza adem�s porque por efecto del achatamiento de los polos el radio ecuatorial es mayor que el polar.
En conclusi�n, podemos decir que la gravedad experimentada por un cuerpo en la superficie de la Tierra tiene un efecto latitudinal.
Es posible obtener una f�rmula general para calcular este efecto latitudinal
o, en otras palabras, calcular la gravedad te�rica en un lugar dado, si se cuenta
con una expresi�n matem�tica simple que describa la forma de la Tierra as� como
valores de la gravedad medidos en algunos puntos de la superficie de la misma.
Desde luego, una esfera podr�a ser utilizada para describir la forma del planeta,
pero sabemos que esto es poco real. En la actualidad se utiliza un elipsoide
de revoluci�n para describir matem�ticamente al planeta. Otros cuerpos geom�tricos
m�s reales, por ejemplo un elipsoide triaxial, resultan demasiado complicados
para su empleo geod�sico (v�ase el Ap�ndice B). La adopci�n de elipsoides de
referencia es tarea de organismos cient�ficos internacionales, entre ellos,
la Uni�n Astron�mica Internacional (IAU) y la Uni�n Internacional
de Geodesia y Geof�sica (IUGG). La f�rmula adoptada actualmente
est� dada por la siguiente expresi�n:
donde f es la latitud. Esta f�rmula, adoptada por
la IUGG en 1967, es conocida como f�rmula del sistema geod�sico
de referencia (GRS 67). El valor de gT en el ecuador (f
= 0) es el resultado del ajuste estad�stico de la red internacional de medidas
gravim�tricas.
En este punto es conveniente hacer una referencia al grav�metro, nombre del instrumento utilizado en este tipo de investigaciones. Existen b�sicamente dos tipos de grav�metros: los de determinaci�n absoluta de la gravedad y los de determinaci�n relativa.
El primer tipo de grav�metros nos permite obtener el valor absoluto de la gravedad en un sitio dado. Durante mucho tiempo se utilizaron e incluso actualmente siguen us�ndose el p�ndulo y la ca�da libre de un cuerpo en el vac�o para calcular la gravedad. Tanto el periodo de un p�ndulo como el tiempo de ca�da de un cuerpo en el vac�o son funciones de g. Naturalmente, el problema de metrolog�a es m�s complejo que el principio en que est�n basadas ambas determinaciones. En efecto, tanto el experimento del p�ndulo como el de ca�da libre deben realizarse en el vac�o, bajo condiciones controladas y con dispositivos elaborados cuidadosamente. En estas condiciones, la gravedad puede determinarse con exactitudes del orden de 0.001 cm/seg2 o, en unidades geof�sicas, de un miligal. La unidad miligal es la mil�sima parte de 1 gal (1 cm/seg2), denominada as� en honor a Galileo. En estas unidades la gravedad promedio en la superficie de la Tierra es de alrededor de 980 gales o 98 x 104 miligales.
Los grav�metros de determinaci�n relativa de g son instrumentos que permiten la evaluaci�n de la gravedad de un sitio con respecto a otro. Usualmente consisten en sistemas de el�sticos y p�ndulos en equilibrio inestable. La figura 27 muestra un diagrama simplificado del mecanismo de un grav�metro.
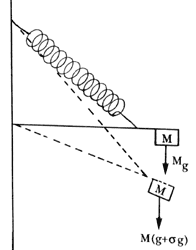
Figura 27. Esquema de un grav�metro tipo Lacoste & Romberg.
Estos grav�metros tienen resoluciones desde un d�cimo de miligal hasta mil�simos de miligal y son ampliamente utilizados cuando se quieren obtener planos de anomal�as gravim�tricas, puesto que en tal caso basta referir las medidas a un punto base y no es necesario llevar a cabo determinaciones absolutas de la gravedad.
Regresando al tema de esta secci�n, una vez que se ha determinado el valor de la gravedad en un sitio podemos tomar la diferencia entre el valor te�rico y el observado go:
Si la Tierra fuera homog�nea y correspondiera exactamente con el elipsoide, la diferencia entre ambos valores ser�a cero. Sin embargo, �ste no es el caso; la superficie de la Tierra tiene una topograf�a y una distribuci�n de masa irregular, es decir, est� compuesta por rocas de muy diversas densidades. As� que la diferencia Dg es debida tanto al relieve de la Tierra como a la distribuci�n de masas en su interior. Es posible eliminar el efecto del relieve terrestre a trav�s de algunas correcciones a los datos observados, que toman en cuenta tanto las alturas y la presencia o deficiencia de materiales sobre el nivel del mar como la topograf�a. Si se realizan estas correcciones, obtendremos:
donde gT es el efecto del relieve. �sta ser�a la diferencia encontrada en una Tierra que no tuviera relieve y su superficie estuviera dada por el nivel de un mar universal. A esta superficie se le llama geoide y no debe confundirse con el elipsoide, que es la figura geom�trica simple que mejor describe al geoide.
Nuevamente, si la Tierra no tuviera heterogeneidades laterales Dgb tendr�a un valor igual a cero. Como esto no es as�, gb es el residuo o anomal�a gravim�trica debida directamente a la distribuci�n de masas en el interior de la Tierra. A gb se le conoce como anomal�a de Bouguer en honor a Pierre Bouguer, geodesta franc�s que entre otras cosas determin� las dimensiones de un arco de longitud en los Andes.
La figura 28 nos muestra las anomal�as de Bouguer en el planeta. A grandes rasgos podemos ver que existen anomal�as fuertemente negativas en las grandes cordilleras y positivas en los oc�anos. Éstas no son debidas a anomal�as de masa en la corteza, puesto que, de ser as�, �c�mo se explica la correspondencia entre topograf�a y anomal�as? Tal correspondencia, adem�s, se relaciona con el hecho mismo de la existencia de una topograf�a muy irregular, porque �c�mo pueden existir enormes monta�as y fosas profundas sin que la fuerza de gravedad y de los elementos tiendan a nivelarla? La respuesta a estas preguntas proporciona gran informaci�n sobre la estructura de la corteza y se puede resumir en una palabra: isostasia.
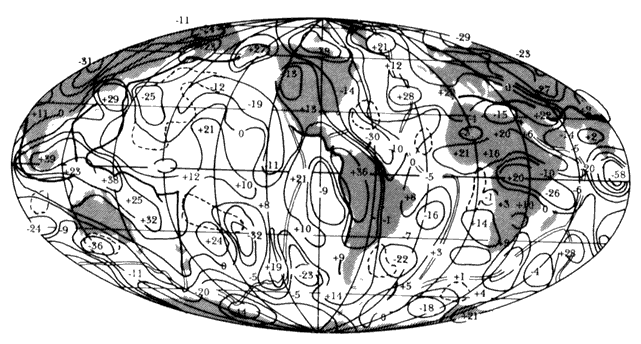
Figura 28. Mapa de anomal�as gravim�tricas globales.
Leonardo da Vinci, con su penetrante sentido de observaci�n, escribi� desde
el siglo XIV:
| Aquella parte de la superficie de cualquier cuerpo pesado que es m�s ligera se distanciar� m�s de su centro de gravedad. |
En 1749, Bouguer, miembro de la Comisi�n Geod�sica Francesa enviada a Per�, public� un libro llamado La figure de la Terre. En �ste expresaba su convicci�n de que la atracci�n efectiva sobre la masa de un p�ndulo debida a la enorme masa de los Andes es mucho menor de lo que cabr�a esperar.
Casi 100 a�os despu�s Everest llevaba a cabo la determinaci�n de la longitud de arco en la India. Al hacer determinaciones de latitud entre las ciudades de Kaliana y Kalianpur, encontr� que en esta �ltima hab�a una diferencia de 5.24 segundos entre la latitud determinada astron�micamente y la obtenida geod�sicamente. En este punto es necesario precisar que la latitud astron�mica se obtiene observando la posici�n de una estrella con respecto a la vertical dada por la plomada. La latitud geod�sica se obtiene midiendo por m�todos topogr�ficos la posici�n de Kalianpur con respecto a la de Kaliana. La diferencia estriba en la cercan�a de los Himalayas a la ciudad de Kalianpur. En efecto, la masa de los Himalayas ejerce una atracci�n gravitatoria sobre la masa de la plomada, desvi�ndola de la "verdadera" vertical (Figura 29).
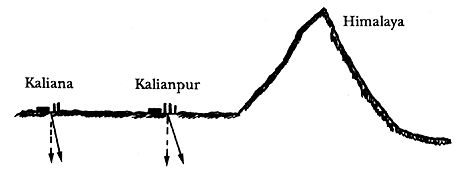
Figura 29. La atracci�n de la plomada por los Himalayas introduce un error en la determinaci�n de la latitud cuando se toma como referencia. El �ngulo i en la figura est� grandemente exagerado.
Este efecto es el que hab�a sido observado por Bouguer en los Andes y se�alado en su libro sobre la figura de la Tierra.
En 1854 el archidi�cono ingl�s J. H. Pratt public� sus c�lculos sobre la atracci�n de los Himalayas. Seg�n �stos, la diferencia de latitudes deber�a ser de 15.88 segundos y no los 5.24 encontrados por Everest. A continuaci�n Pratt se propuso explicar la inconsistencia y en 1959 public� su teor�a, seg�n la cual la diferencia era debida a las distintas densidades de los bloques que componen la corteza terrestre. En la figura 30(a) podemos ver que si las zonas monta�osas est�n compuestas por bloques cuya densidad es menor que la de zonas de menor relieve y asimismo las grandes fosas oce�nicas est�n soportadas por bloques de mayor densidad, la frontera entre corteza y manto est� a una misma presi�n y la atracci�n de las monta�as ser� menor por su menor densidad con respecto a la densidad de un bloque con menor relieve.
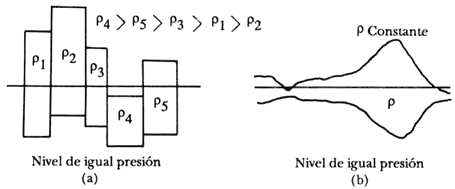
Figura 30. Modelos isost�ticos de Pratt (a) y Airy (b).
Existe otra manera de explicar la deficiencia, que fue propuesta por otro brit�nico. En 1855 G.B. Airy plante� que las grandes monta�as est�n compensadas por grandes protuberancias o ra�ces que se hunden en lo que se identifica modernamente como el manto, el cual posee una densidad superior a cualquier material de la corteza. En este modelo la densidad promedio de la corteza es igual en todas partes (Figura 30b). Una analog�a con este modelo puede verse en unos troncos de �rbol flotando en el agua. La madera busca una posici�n de equilibrio y para cada porci�n que sobresale del agua existe una porci�n bajo la misma. La existencia de estas ra�ces que se hunden en un material m�s denso ocasiona una deficiencia de masa que compensa la atracci�n de la monta�a.
Con el desarrollo de las t�cnicas sismol�gicas fue posible detectar la discontinuidad de Mohorovicic y observar que efectivamente es m�s profunda en los continentes que en los oc�anos; aunque esto no implica que la teor�a de Pratt sea incorrecta, y el mecanismo propuesto por �l tambi�n interviene en el proceso de equilibrio de la corteza, o como se le conoce actualmente, equilibrio isost�tico. Por supuesto, no todas las regiones de la Tierra han alcanzado equilibrio isost�tico. Este mecanismo tiene lugar a lo largo de millones de a�os, puesto que el manto se comporta como un fluido de gran viscosidad. Aqu� es necesario aclarar un punto. Hemos mencionado que el manto tiene una composici�n l�tica. �C�mo puede entonces comportarse como un fluido? La respuesta se encuentra en las escalas de tiempo. En efecto, las rocas nos parecen un buen ejemplo de un cuerpo s�lido. Si por desgracia un trozo de roca nos cae en la cabeza estaremos a�n m�s convencidos del punto. Sin embargo, si someti�ramos un bloque de roca a altas presiones y temperaturas por tiempos muy largos ver�amos que �sta se deforma sin recuperar su forma anterior, es decir, la roca se comporta en este caso como un s�lido pl�stico. Si se la somete a esas condiciones por tiempos mucho mayores su conducta se asemejar� a la de un fluido de alta viscosidad.
Volviendo al tema principal, dec�amos que no toda la corteza est� compensada isost�ticamente. Por ejemplo, enormes regiones de Canad� y Fenoscandia que fueron cubiertas por los hielos durante las glaciaciones contin�an sufriendo lentos levantamientos para compensar la deficiencia de masa que dej� el retroceso de los hielos en �pocas geol�gicamente recientes. Tampoco est�n compensadas aquellas zonas en que el volcanismo reciente ha creado edificios y en general aquellas en que la din�mica terrestre ha producido recientemente movimientos orog�nicos.
Mercurio, Venus, la Tierra y Marte son llamados planetas terrestres. Dentro de este grupo, la Tierra tiene el campo magn�tico m�s grande. En una primera aproximaci�n, �ste puede representarse por un dipolo magn�tico situado en su centro con una inclinaci�n de 11 grados con respecto al eje geogr�fico y con una magnitud de 0.6 a 0.7 oersteds.
A pesar de que tanto el origen como las caracter�sticas del campo magn�tico son temas de gran inter�s y relevancia para el estudio del planeta, por su extensi�n no es posible tratarlos en un breve espacio. As� pues, nos referiremos solamente al m�todo que se emplea para conocer la estructura de la corteza terrestre.
La mayor�a de las rocas contienen peque�as cantidades de magnetita y otros �xidos de hierro, as� como algunos sulfuros que poseen propiedades ferromagn�ticas. Esto quiere decir que tales minerales pueden adquirir un campo magn�tico si cristalizan en presencia de un campo magn�tico. En el caso de los minerales magn�ticos, su magnetizaci�n es adquirida del campo magn�tico terrestre al cristalizar a partir de un magma. La intensidad de la magnetizaci�n inducida, o el momento magn�tico por unidad de volumen adquirido por un cuerpo en presencia de un campo externo (H) puede ser escrito como:
donde X es una constante llamada susceptibilidad magn�tica. Como puede observarse, entre m�s grande es X m�s grande es el campo magn�tico inducido.
Dado que la magnetita es un mineral con alta susceptibilidad magn�tica, su contenido en una roca determina significativamente la susceptibilidad de esta �ltima. La concentraci�n de magnetita y en general de minerales ferromagn�ticos en las rocas es muy baja, pero se presenta en suficiente cantidad para poder ser medida y ofrecer un contraste entre rocas de diferentes tipos.
El magnetismo en rocas se mide por medio de los instrumentos llamados magnet�metros, y para el estudio de la corteza se hacen determinaciones relativas de manera semejante al m�todo gravim�trico. Tanto en magnetometr�a como en gravimetr�a se suele utilizar la componente vertical del campo en cuesti�n. En magnetometr�a se puede utilizar tambi�n la declinaci�n (Figura 31) pero la componente vertical es usualmente m�s sencilla de interpretar.
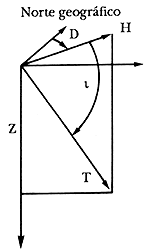
Figura 31. El vector de campo geomagnético. H es la componente horizontal, Z la vertical, D es la declinación e i la inclinación.
En cuanto a los magnet�metros, existe una gran variedad de instrumentos basados en diferentes principios: la deflexi�n de una br�jula, el desbalance de un par de bobinas, la precesi�n libre de protones, el bombeo �ptico de electrones, etc. Magnet�metros de estos tipos son los m�s utilizados actualmente en el trabajo de campo, aunque existen otros de gran sensibilidad para trabajo de laboratorio.
En magnetometr�a se suele utilizar una unidad m�s peque�a que el oersted y que es conocida como gamma (g):
En estas unidades se pueden detectar variaciones en el campo magn�tico de algunas decenas de gamma, dependiendo del instrumento utilizado. Un aspecto que le da gran versatilidad a la investigaci�n magnetom�trica es que puede hacerse desde aviones a los que se han adaptado magnet�metros que usualmente son arrastrados por cables a cierta distancia del avi�n para evitar el campo magn�tico propio de la aeronave. De esta manera es posible obtener datos magnetom�tricos de �reas extensas en corto tiempo y con bastante densidad (Figura 32).
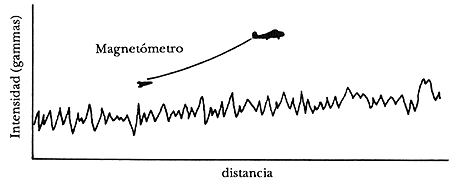
Figura 32. Perfil t�pico de un levamtamiento aeromagn�tico.
Los datos magn�ticos son configurados y presentados como mapas de isoanomal�as magn�ticas. La figura 33 nos muestra un ejemplo de un mapa de anomal�as magn�ticas. La interpretaci�n de mapas tanto magnetom�tricos como gravim�tricos requiere del procesamiento de los datos con m�todos matem�ticos que permiten resaltar o disminuir determinados rasgos y son posteriormente modelados para dilucidar las estructuras que los causan.
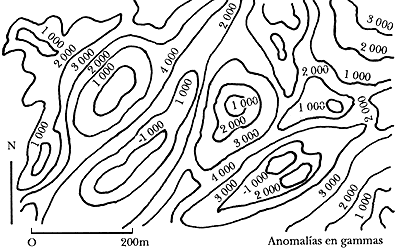
Figura 33. Mapa t�pico de anomal�as magn�ticas. Los contornos est�n dados en gammas.
Incidentalmente, durante mucho tiempo el m�todo gravim�trico no pudo ser llevado a cabo a bordo de aeronaves puesto que los movimientos de las mismas introduc�an aceleraciones que alteraban las determinaciones de gravedad. Es un fruto de la tecnolog�a de los a�os setenta y ochenta el que este m�todo se pueda llevar a la pr�ctica, aunque a�n dista de tener la facilidad y econom�a del m�todo magnetom�trico.
ESTRUCTURA DE LA CORTEZA TERRESTRE
A los m�todos que acabamos de mencionar los geof�sicos a�aden muchas otras t�cnicas de investigaci�n: entre �stas cabe mencionar la medici�n del flujo de calor terrestre y la penetraci�n de las ondas el�ctricas en el interior de la Tierra. Los cient�ficos utilizan tanta informaci�n como les es posible, ya que cada m�todo aporta informaci�n complementaria para resolver el rompecabezas que constituye la estructura cortical.
Con base en estos m�todos ha sido posible estudiar con detalle la estructura de algunas regiones de la corteza terrestre. Durante mucho tiempo, dadas las limitaciones de los datos geol�gicos y geof�sicos, se pens� que la corteza ten�a una estructura simple compuesta a grandes rasgos por dos estratos, uno inferior bas�ltico y otro superior gran�tico, separados por una discontinuidad a la que se dio el nombre de discontinuidad de Conrad. Esta discontinuidad se detecta efectivamente en algunas �reas, donde tiene profundidades que oscilan entre los 17 y 25 km. Sin embargo, con la acumulaci�n de datos este sencillo esquema no es ya satisfactorio y la corteza revela una estructura mucho m�s complicada.
Una clasificaci�n general de los tipos de corteza, dada por J. Brune en 1969, aparece en el cuadro 8:
UADRO 8. Clasificaci�n de la corteza propuesta por Brune (1969)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
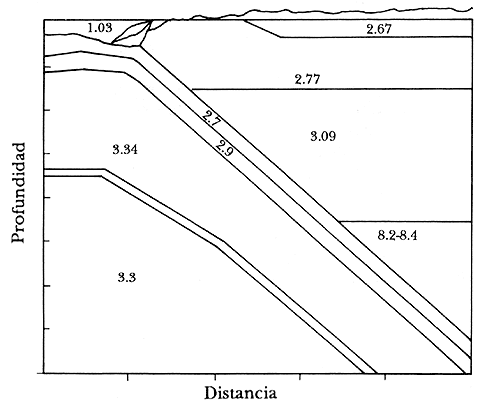
Las figuras 34 y 35 muestran segmentos de la corteza en M�xico, obtenidos por refracci�n s�smica y consistentes con medidas de gravedad. El primero es un perfil perpendicular a la trinchera de Acapulco. Los n�meros entre par�ntesis indican las densidades y los dem�s las velocidades de las ondas P. La figura 34 es un perfil paralelo a la zona de trinchera. Finalmente, la figura 36 nos muestra un segmento de la estructura oce�nica en el Atl�ntico.
Como podemos observar, la complejidad de la corteza terrestre nos impide hacer generalizaciones sobre su estructura, y muestra que cada porci�n de la misma requiere de estudios detallados y espec�ficos para dilucidarla. La corteza terrestre es un delgado estrato en constante evoluci�n y transformaci�n que incluye continuos engrosamientos y adelgazamientos; la actividad magm�tica, las fuerzas erosivas y la din�mica de la litosfera son factores que determinan esta evoluci�n.
Es necesario hacer aqu� una aclaraci�n: la evoluci�n y comportamiento de la corteza est�n �ntimamente relacionadas con la tect�nica de placas. No nos detendremos detalladamente en esta teor�a, cuyo tratamiento podr�a ocupar un solo volumen, pero s� aclararemos el significado de la afirmaci�n anterior.
Sabemos actualmente que los continentes han ocupado posiciones relativas diferentes en el pasado. Partes de la corteza continental actual formaron alguna vez un solo continente, al que se ha llamado Pangea. Este protocontinente se fragment� en varias partes como resultado del movimiento de las diferentes placas que constituyen el cascar�n externo de la Tierra llamado litosfera. Esta capa externa tiene un espesor de alrededor de 100 km, y tanto la corteza como la parte superior del manto constituyen parte de la misma. La litosfera "flota" sobre otro casquete conocido como astenosfera. Debe tomarse en cuenta que esta clasificaci�n de la parte superior de la Tierra no contradice a la descrita anteriormente, cuando nos referimos a su estructura interna. Mientras que la clasificaci�n que vimos antes indica cambios qu�micos y f�sicos, la definici�n de litosfera y astenosfera se basa esencialmente en su respuesta mec�nica. Volviendo a la figura 17(b), podemos ver que la regi�n a, la capa r�gida de alta velocidad, es precisamente la litosfera y el estrato b la astenosfera.
|
|
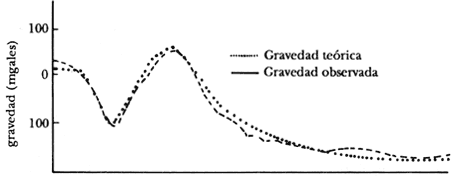
Figura 34. Secci�n de la corteza perpendicular a la costa de Acapulco, obtenido por refracci�n s�smica y gravimetr�a. Los valores entre par�ntesis son las densidades de las capas; los dem�s valores son sus velocidades s�smicas. La curva superior es la gravedad te�rica comparada con la observada (adaptada de Singh y colaboradores, 1985).
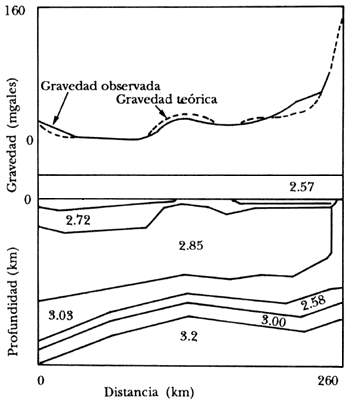
Figura 35. Secci�n de la corteza entre Puerto Maldonado y Puerto �ngel. Los valores indicados son la densidad de la capa en gr/cm. La gr�fica superior es la comparaci�n entre las gravedades te�rica y observada (adaptada de Nava y colaboradores, 1988).
En cuanto a la composici�n qu�mica de la corteza, una estimaci�n promedio de �sta hecha por A. B. Ronov y A. A. Yaroshevsky aparece en el cuadro 9. Las estimaciones de otros autores no difieren considerablemente de �sta.
Estos mismos autores estimaron las proporciones de rocas y minerales por volumen que aparecen en la corteza. Sus datos aparecen en el cuadro 10.
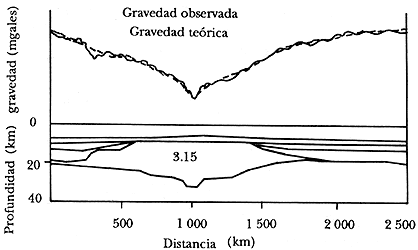
Figura 36. Mapa de anomal�as magn�ticas de una secci�n del Atl�ntico (adaptado de Talwani y colaboradores, 1965).
UADRO 9. Composici�n qu�mica de la corteza terrestre.
|
||
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
FUENTE: Ronov y Yaroshevsky, 1969. |
||
UADRO 10. Composici�n petrol�gica y mineral�gica de la corteza
|
|
|
|
|
|
|
|
|
|
|
| Tipo de roca: | |
|
|
|
|
|
|
|
|
|
| Mineral: | |
|
|
|
|
|
|
|
|
|
| Carbonatos |
|
| Otros |
|
|
|
|
FUENTE: Ronov y Yaroshevsky, 1969. |
|
En 1963 A. E. J. Engel public� una s�ntesis de las edades de las grandes estructuras tect�nicas de Norteam�rica. La figura 37 muestra el patr�n de edades de las grandes formaciones continentales. Como puede verse, el continente consiste de un n�cleo antiguo rodeado por rocas de edad decreciente, donde la �ltima es de 5 a 6 veces m�s joven que el n�cleo. Este hecho sugiere que los continentes han crecido por acrecentamiento de sus m�rgenes. Es sin embargo dif�cil determinar a qu� raz�n han crecido, puesto que las rocas m�s j�venes pueden provenir del reprocesamiento de las partes antiguas o de adici�n nueva del manto. En este sentido, estudios isost�ticos que muestran un alto grado de compensaci�n han arrojado cierta luz sobre el problema, aunque no bastan todav�a para arrojar una conclusi�n general.
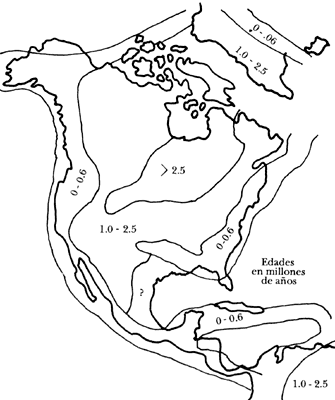
Figura 37. Mapa generalizado de las edades de las rocas de Norteam�rica (tomado de Engel, 1963).
El mismo comentario puede hacerse sobre los estudios geoqu�micos. Cabe mencionar,
en particular, a los estudios isot�picos. Como vimos en la primera parte de
este libro, el Sr-87 puede provenir del decaimiento del Rb-87; la comparaci�n
de las razones de Sr-87/Sr-86 en varias muestras de rocas continentales permite
adelantar algunas conclusiones. El valor del Sr-87/Sr-86 en rocas representativas
del manto es de 0.704 
0.002. La gran diferencia entre este valor y los valores de rocas de la corteza,
por ejemplo de algunas rocas prec�mbricas (Sr-87/Sr-86 = 0.712-0.726), indican
que la formaci�n de la corteza comenz� en una etapa muy temprana de la historia
del planeta, pues de lo contrario dichas rocas no habr�an logrado tanta diferenciaci�n.
La figura 38 nos indica los rangos de valores de estroncio en rocas de diferentes
ambientes.
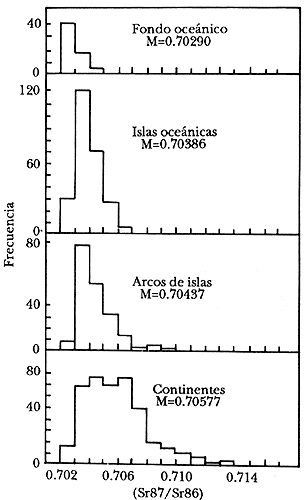
Figura 38. Gr�fica de frecuencia de valores de Sr-87/Sr-86 en diferentes ambientes tect�nicos (tomada de Wyllie, 1971).
En estos histogramas podemos apreciar la complejidad en la evoluci�n de las rocas continentales comparadas con las oce�nicas (aunque la interpretaci�n de los resultados para estas �ltimas tampoco es muy sencilla).
Las t�cnicas que hemos mencionado forman parte de las herramientas esenciales de las ciencias de la Tierra para el estudio local de la corteza terrestre. La investigaci�n sobre el tema es incesante y alg�n d�a permitir� realizar una s�ntesis general que nos permita entender mejor la din�mica del planeta.
La investigaci�n no s�lo es de inter�s cient�fico sino pr�ctico. La informaci�n que estos estudios arrojen permitir� comprender mejor la g�nesis de los grandes yacimientos minerales, las manifestaciones destructivas de la Tierra, como el vulcanismo y la sismicidad, y otros fen�menos del planeta que est�n �ntimamente asociados con las actividades del hombre.
