AP�NDICE B
LA FORMA DE LA TIERRA Y LA GRAVEDAD TE�RICA
La noci�n de una Tierra esf�rica data de la �poca de los antiguos griegos. La idea se atribuye a Pit�goras y sus disc�pulos y fue defendida por Plat�n y Arist�teles. El problema de la figura de la Tierra no deja de tener sus implicaciones pr�cticas, ya que desde los inicios de la cartograf�a se planteaba la necesidad de saber si las distancias a lo largo de un arco de longitud eran equivalentes a las de un arco de latitud. En el siglo III a.C. Erat�stenes de Alejandr�a se embarc� en la determinaci�n de la circunferencia de la Tierra. Erat�stenes hab�a notado que en la actual Aswan los rayos del Sol incid�an verticalmente hacia el fondo de un pozo mientras que en Alejandr�a formaban un �ngulo de 7.2 con la vertical. Resulta entonces que la circunferencia de la Tierra es 50 veces la distancia de Aswan a Alejandr�a puesto que 7.2 es la cincuentava parte de la circunferencia (360°). Se dice que Erat�stenes calcul� la distancia entre ambas ciudades calculando la velocidad promedio de los camellos y el tiempo que tomaba realizar el viaje. Su resultado en unidades actuales, con la incertidumbre con que se conocen las unidades antiguas, es de alrededor de 40 000 km, una cifra muy cercana a los c�lculos modernos.
Hacia el siglo XV, se aceptaba generalmente la noci�n de una Tierra
esf�rica. Newton, sin embargo, en un famoso libro conocido abreviadamente como
Principia, hizo notar que, debido a la rotaci�n de la Tierra, las partes
m�s alejadas de su eje de rotaci�n deb�an sufrir un efecto centr�fugo de mayor
magnitud. Por lo tanto, la forma de la Tierra deb�a ser la de una esfera oblada,
es decir, achatada en los polos. Newton calcul� el achatamiento como de 1 parte
en 230. Hoy consideramos un valor m�s correcto como de 1 parte en 298.25, y
el di�metro polar de unos 43 km m�s corto que el ecuatorial. En el siglo XVIII
los franceses, dirigidos por Domenico y Jacques Cassini, se dieron a la tarea
de medir geod�sicamente la diferencia latitudinal en la longitud del arco, realizando
mediciones en el Norte y Sur de Francia. Desafortunadamente la diferencia de
curvatura entre ambas regiones result� muy peque�a para poder ser observada
con los instrumentos y t�cnicas de la �poca, y se lleg� a la err�nea conclusi�n
de que la Tierra era prolada, es decir, que ten�a mayor curvatura en los polos
que en el ecuador (una analog�a exagerada ser�a la forma de un pepino). El resultado
mencionado ocasion� tal pol�mica con tintes nacionalistas que entre 1735 y 1736
un par de expediciones francesas partieron hacia regiones tan remotas como Per�
y Laponia. Los resultados se conocieron algunos a�os m�s tarde y condujeron
a la conclusi�n correcta: la Tierra es un esferoide achatado en sus polos.
En 1957, con el nacimiento de la era espacial y de los sat�lites artificiales, se pudo observar que la forma de la Tierra era menos simple que un esferoide sim�trico achatado en los polos. Pero antes de proseguir, es necesario hacer algunas consideraciones generales sobre lo que se quiere decir cuando se habla de la forma de la Tierra. Ésta no es, desde luego, la formada por la superficie real de la Tierra con sus monta�as, fosas y planicies. Dicha superficie dista mucho de poder ser descrita por una figura geom�trica simple y es en extremo irregular. El problema se simplifica si, siguiendo a Newton, imaginamos una superficie global sobre la cual se elevan las monta�as y planicies de los continentes y desde la cual descienden las profundas fosas oce�nicas. Dicha superficie es la definida por el nivel de los oc�anos y su continuaci�n a trav�s de los continentes por canales imaginarios que los cortan. Dicha superficie recibe el nombre de geoide, de manera que el problema de determinar la forma de la Tierra consiste en expresar matem�ticamente la figura del geoide. Ahora bien, aunque dicha figura es menos irregular que la superficie real de la Tierra, no es tampoco una figura geom�trica simple. Sin embargo, puede representarse matem�ticamente como la suma de varios t�rminos, llamados arm�nicos, que contribuyen en proporciones diversas a conformar la figura del geoide. La figura 39 muestra los primeros cinco arm�nicos de la serie.
Volviendo al tema de los sat�lites artificiales, �stos nos proveen de informaci�n sobre la contribuci�n de los arm�nicos a la suma total. En la actualidad se tiene informaci�n sobre un gran n�mero de arm�nicos del geoide y la forma de la Tierra se conoce con gran precisi�n. Los sat�lites son utilizados, desde el punto de vista de la geodesia, como puntos de referencia muy precisos en sistemas de triangulaci�n o a trav�s de las fluctuaciones en su trayectoria por efecto de la atracci�n gravitacional de la Tierra que a su vez est� relacionada con la forma del geoide. Sin embargo, desde un punto de vista geof�sico, nos interesa adoptar una figura de la Tierra que nos permita calcular el efecto latitudinal en la gravedad del planeta debido a la rotaci�n del mismo. Desde luego, la forma del geoide ser�a la figura ideal para llevar a cabo estos c�lculos; pero, como ya hemos visto, resulta ser una figura muy compleja cuyo empleo hace dif�cil el c�lculo en cada sitio en que se lleve a cabo una medida gravim�trica. Por otro lado, tanto la resoluci�n de nuestros instrumentos como la interpretaci�n de los datos har�an injustificables dichos c�lculos. As� se ha preferido utilizar un elipsoide de revoluci�n (dos semiejes iguales y el tercero menor que los anteriores) como la figura que mejor describe al geoide (Figura 40). A pesar de que tambi�n se han introducido elipsoides triaxiales (con los tres semiejes distintos), el elipsoide de revoluci�n contin�a siendo la referencia adoptada de manera internacional, pues incluso el elipsoide triaxial resulta matem�ticamente muy complicado para poder ser utilizado en los c�lculos rutinarios.
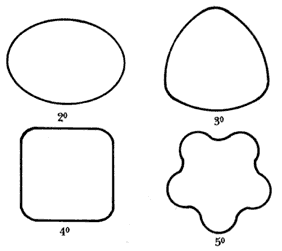
Figura 39. Primeros cinco arm�nicos de la forma de la Tierra (el primer arm�nico es una esfera).
El adjetivo "mejor", utilizado anteriormente, puede entenderse en t�rminos
de las medidas llevadas a cabo en un �rea en particular y as�, en diferentes
pa�ses, se han utilizado elipsoides diferentes que se ajustan bien a una regi�n
determinada pero no a todo el planeta. Con el desarrollo de la gravimetr�a y
la geodesia f�sica fue necesaria la utilizaci�n de estaciones gravim�tricas
en todo el planeta, y esto supuso la uniformizaci�n de las medidas de gravedad
por medio de un elipsoide est�ndar. En 1924 la asamblea de la Asociaci�n Internacional
de Geodesia (International Asociation of Geodesy,—IAG—)
reunida en Madrid, resolvi� adoptar un elipsoide internacional de referencia.
En 1964, la abundante informaci�n de los sat�lites hizo necesario el cambio
de dicho elipsoide. Ese a�o, la Uni�n Astron�mica Internacional (International
Astronomical Union —IAU—), adopt� un nuevo elipsoide de
referencia internacional, mismo que fue luego adoptado por la Uni�n Internacional
de Geodesia y Geof�sica (International Union of Geodesy and Geophysics —IUGG—).
Figura 40. Representaci�n esquem�tica exagerada de la diferencia entre geoide y elipsoide.
Para establecer una f�rmula de gravedad te�rica se requiere, adem�s, del establecimiento
de una red mundial de determinaciones gravim�tricas que permitan conocer con
la mayor exactitud posible el valor de la gravedad en el ecuador. Los valores
de dicha red se refer�an en el pasado a un lugar en el que se determinaba la
gravedad absoluta con la mayor exactitud posible. La primera de dichas redes
fue la adoptada en la XIII Conferencia de la IAG celebrada
en Par�s en 1900. Los valores de esta red estaban referidos a medidas hechas
en Viena, por lo que se le llam� Sistema de Gravedad de Viena (Vienna Gravity
System). En 1909 la IAG cambi� dicho sistema por otro referido
a la ciudad alemana de Potsdam (Potsdam Gravity System).
El elipsoide adoptado en 1924 y el sistema de Potsdam permitieron obtener una f�rmula te�rica de gravedad que a�n hoy se utiliza:
En 1967 la IUGG adopt� un nuevo sistema gravim�trico, basado no en un solo sitio sino en una red de medidas absolutas. Este sistema se denomina Sistema Geod�sico de Referencia-67, Geodetic Reference System 67 (GRS-67). En su reuni�n de agosto de 1971, la XV Asamblea General de la IUGG, reunida en Mosc�, tom� la resoluci�n de adoptar el GRS-67 como base de la red internacional de estandarizaci�n gravim�trica. La f�rmula te�rica basada en el GRS-67 est� dada por la f�rmula de p�ginas anteriores que repetimos a continuaci�n:
