VIII. LA CONJETURA DE MIZEL
A CONTINUACIÓN vamos a platicar sobre una conjetura que estuvo rondando, a principios de los años sesentas, en los círculos matemáticos interesados en la convexidad geométrica. Esta conjetura fue propuesta por V. Mizel y fue resuelta en el año de 1961 por A. S. Besicovitch.
Pensemos en un círculo. Ponga usted sobre él un rectángulo de tal forma que tres de sus esquinas queden colocadas sobre la frontera del círculo. Es intuitivamente claro que entonces la cuarta esquina estará también sobre la frontera del círculo. Esta propiedad del círculo no la comparten otras figuras, como por ejemplo las elipses o el triángulo de Reuleaux. (ver figura VlII.1). La conjetura de Mizel afirmaba que sólo el círculo posee esta curiosa propiedad.
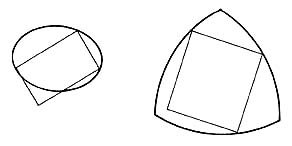
Supongamos que usted tiene una figura convexa Q con la propiedad de que cada vez que usted pone un rectángulo de tal forma que tres de sus esquinas quedan colocadas sobre la frontera de Q entonces misteriosamente, la cuarta esquina también queda colocada sobre la frontera de Q. Empezaremos convenciéndonos de que esta misteriosa figura convexa Q tiene que ser una figura de ancho constante.
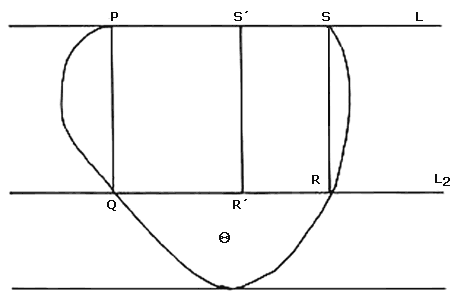
Para demostrar que Q es una figura de ancho constante bastará ver que toda normal de Q es una binormal. Sea PQ una normal de Q (ver figura VIII .2) y sea L la línea soporte de Q que pasa por P y es perpendicular a PQ. Sea L1 la otra línea soporte de Q paralela a L. Queremos ver que Q está realmente sobre L1.
Sea L2 la línea paralela a L que pasa por Q. Como Q es una figura convexa y Q está en la frontera de Q, la línea corta a Q exactamente en el segmento QR donde R es un punto de la frontera de Q. Consideremos el rectángulo PQRS determinado por los puntos P, Q y R. Claramente S pertenece a la frontera de Q, pero entonces, siendo Q convexo, todo el segmento PS pertenece a la frontera de Q. Tomemos ahora cualquier punto S' en el segmento PS y consideremos el rectángulo PQR'S' determinado por los puntos P, Q y S. Tenemos entonces que R' está en la frontera de Q. Como S' fue en realidad cualquier punto del segmento PS, entonces todo el segmento QR pertenece a la frontera de Q, por lo que la línea L, al tocar a Q sólo en puntos frontera, tiene que ser necesariamente una línea soporte de Q. Es decir, la línea L2 es realmente la línea soporte L1, el punto Q está en L1=L2 y por lo tanto PQ es una binormal y no sólo una normal de Q. Hemos comprobado que toda normal de Q es una binormal de Q, lo que muestra que Q es una figura de ancho constante.
Demostrar finalmente que Q es un círculo que requiere de más trabajo; sin embargo, en este momento es interesante notar que la versión tridimensional de este problema es, en virtud de nuestro trabajo previo, mucho más sencilla de demostrar.
Supongamos que un sólido Q tiene la propiedad de que cada vez que un rectángulo tiene tres de sus esquinas en la frontera de Q entonces la cuarta esquina está también en la frontera de Q. Es fácil ver que Q es una esfera puesto que, en virtud de lo anterior, cada una de sus tajadas es una figura de ancho constante y sabemos, por el capítulo anterior, que la esfera es el único sólido con la propiedad de que todas sus tajadas son de ancho constante.
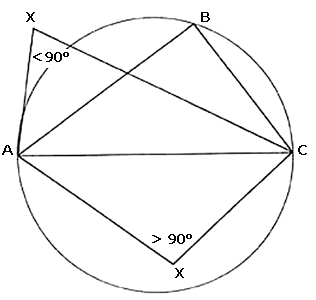
Antes de continuar con nuestro problema original, recordemos un hecho simple de la geometría. Supongamos que tenemos un triángulo rectángulo ABC con hipotenusa AC, es decir, supongamos que en el triángulo ABC, el segmento AB es perpendicular al segmento BC. (ver figura VIII.3) Entonces el círculo y, que tiene al segmento AC como diámetro, pasa por B. Más aún, si un punto X está sobre este círculo, el ángulo AXC tiene exactamente noventa grados; si el punto X está dentro del círculo y entonces el ángulo AXC tiene más de noventa grados y los puntos X exteriores al círculo y son precisamente aquellos puntos para los cuales el ángulo AXC tiene menos de noventa grados.
Volvamos a nuestro problema original. Tenemos una figura de ancho constante Q con la propiedad de que si un rectángulo tiene tres de sus esquinas en la frontera de Q entonces la cuarta esquina también está en la frontera de Q. Queremos ver que Q es realmente un círculo. Lo iremos viendo por partes.
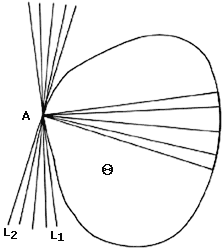
Lo primero que tenemos que notar es que, debido a que Q es de ancho constante, existe por ahí un punto en la frontera de Q por el cual pasa una sola línea soporte. Vamos a encontrar dicho punto. Tomemos A, cualquier punto en la frontera de Q (ver figuraVIII. 4). Si por A pasa una sola línea soporte, ya lo hemos encontrado. Si no, existen dos líneas soporte, L1 y L2 de Q, por A; más aún, cualquier línea que pase por A entre L1 y L2, es línea soporte de Q. Las cuerdas de Q que pasan por A y son perpendiculares a todas estas líneas soporte son binormales de Q y por lo tanto todas ellas poseen la misma longitud. Luego entonces, en la frontera de Q, en la parte opuesta a A, existe un arco de círculo con centro en A. Hemos encontrado el punto que buscábamos, pues por cualquiera de los puntos del interior de este arco de círculo pasa solamente una línea soporte de Q. De ahora en adelante llamémosle A a este punto de la frontera de Q. Notemos que por A pasa una sola línea soporte y por lo tanto una sola binormal de Q.
Existen muchos rectángulos inscritos en Q, es decir, con sus cuatro esquinas sobre la frontera de Q. Algunos de ellos tienen al punto A como una de sus esquinas. Construir de estos últimos es muy fácil; basta seguir una cuerda AB, que no sea una binormal de Q, doblar a noventa grados en B sobre la perpendicular a AB hasta encontrar la frontera de Q, digamos en el punto C. El rectángulo ABCD determinado por los puntos A, B y C tiene sus cuatro esquinas sobre la frontera de Q.
Démosle una dirección a la frontera de Q. Empezando en A y caminando en esta dirección, sobre la frontera de Q, paremos en M la primera vez que encontremos un rectángulo ABMD con diagonal AM inscrito en Q. Notemos que si X es un punto de la frontera de Q que se encuentre, siguiendo esta dirección, entre A y M, entonces la perpendicular a la cuerda AX por X corta a la frontera de Q en un punto Y que se encuentra, siguiendo esta misma dirección, después de M (ver figura VIII .5). Por lo tanto, para cualquier punto X de la frontera de Q que se encuentre entre A y M, el ángulo AXM tiene más de noventa grados y consecuentemente se encuentra dentro del círculo z , que tiene al segmento AM como diámetro. Es decir, el arco AM de la frontera de F se encuentra dentro del círculo z.
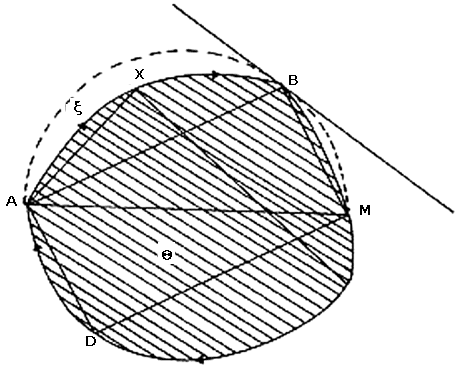
Vamos a demostrar que la cuerda BD, diagonal del rectángulo ABMD, es una binormal de Q. Bastará ver que la línea soporte a Q por B es perpendicular a la cuerda BD. Tracemos el círculo z que tiene a AM como diámetro y pasa por los puntos B y D. Sea L la línea tangente a z por el punto B. Dado que el arco AM de la frontera de Q se encuentra dentro de z, la línea L es una línea soporte de Q que pasa por B. Siendo BD una diagonal del rectángulo ABMD, es claro que la línea L es perpendicular al segmento BD. Es decir, BD es una normal y por lo tanto una binormal de Q.
Ahora que ya sabemos que BD es una binormal de Q, es fácil ver que también la cuerda AM es una binormal de Q, puesto que cualquier cuerda de Q que tenga la misma longitud que la longitud de BD es una binormal de Q.
Volvamos a caminar sobre la frontera de Q,
pero esta vez paremos en el punto N la última vez que encontremos un
rectángulo AGNT inscrito en Q con diagonal
AN. De la misma manera en que verificamos que AM era una binormal
de Q, es posible comprobar —hágalo usted—
que AN es también una binormal de Q,
pero como escogimos el punto A de tal forma que por él sólo pasase una
binormal, el punto M tiene que coincidir con el punto N. Debido
a la forma como encontramos al punto M y el punto N, al coincidir
estos dos, tenemos que todo rectángulo inscrito en Q,
que tiene a A como a una de sus esquinas, tiene forzosamente al segmento
AM como una de sus diagonales. En particular, si X es cualquier
punto de la frontera de Q, distinto de A
y de M, y L es una línea perpendicular a AX por X,
entonces L corta a la frontera de Q
en M, de lo contrario habría un rectángulo inscrito en Q
cuya diagonal no es AM. Es decir, para cualquier punto X en la
frontera de Q, el ángulo AXM tiene
noventa grados y por lo tanto X tiene que estar en el círculo que tiene
a AM como diagonal. Esto es, Q es necesariamente
el círculo con diámetro AM.