VII. SÓLIDOS DE ANCHO CONSTANTE
POR supuesto existen sólidos de ancho constante. Tomemos una dirección en el espacio y planos soporte perpendiculares a esta dirección que aprisionen a un sólido q. La distancia entre estos dos planos es el ancho de q en esta dirección. Un sólido de ancho constante es un sólido con la propiedad de que su ancho es el mismo en cualquier dirección.
Es fácil construir un sólido de ancho constante rotando el triángulo de Reuleaux como lo indica la siguiente figura:
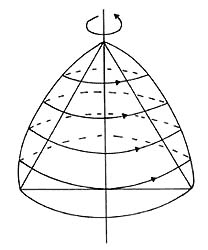
En un sólido de ancho constante h, la distancia entre cualquier par de puntos es menor o igual a h. La razón, al igual que en las figuras de ancho constante, es que si hubiese dos puntos, X y Y a distancia mayor que h el ancho del sólido en la dirección del segmento XY sería mayor que h cuando debe ser h.
Si P y P' son dos planos paralelos a distancia h y Y es un punto de P'; entonces existe un único punto X en P —aquél para el cual el segmento XY es perpendicular a P y a P'— con la propiedad de que la distancia entre Y y X es h. Para cualquier otro punto M en P, la distancia entre Y y M es mayor que h. Es por lo anterior que, de la misma forma como lo demostramos para las figuras de ancho constante:
Si P y P' son planos soporte paralelos de un sólido q de ancho constante, entonces tanto P como P' tienen con q un solo punto de contacto y el segmento que une estos dos puntos es perpendicular tanto a P como a P'.
De lo anterior deducimos que todo sólido de ancho constante h es un sólido convexo con diámetro h.
Llamaremos diámetro de un sólido de ancho constante al segmento de línea que une los puntos de contacto de dos planos soporte paralelos. En forma similar a como fue probado para las figuras, es fácil ver que los diámetros de un sólido de ancho constante h son precisamente los segmentos de línea contenidos en el sólido que tienen longitud h.
Lo siguiente nos permitirá demostrar que un sólido es de ancho constante verificando que todas sus proyecciones son figuras de ancho constante.
Si todas las proyecciones de un sólido q son figuras de ancho constante h, es porque el sólido q es un sólido de ancho constante h y viceversa; las proyecciones de un sólido de ancho constante h son siempre figuras de ancho constante h.
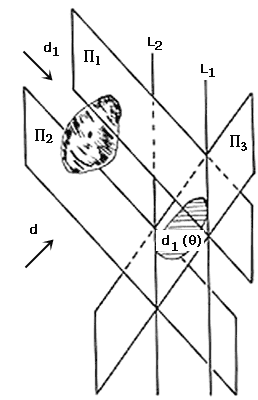
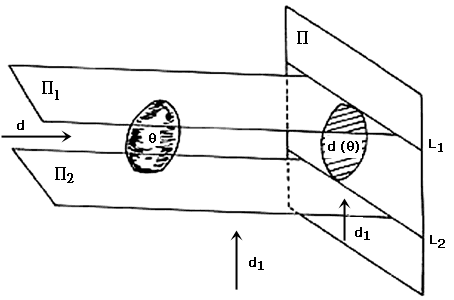
Demostración. Supongamos que todas las proyecciones del sólido q son figuras de ancho constante h. Queremos ver que q es un sólido de ancho constante h (ver figuraVII.2). Tomemos d, una dirección cualquiera —escoja usted una. Llamemos P1 y P2 a los planos soporte de q perpendiculares a la dirección d. Vamos a verificar que el ancho de q en la dirección d, es decir, la distancia entre P1 y P2, es igual a h. Tomemos d1, una dirección perpendicular a d y proyectemos a q en la dirección de d1 sobre el plano P3 —que es perpendicular a d1. Llamemos d1 (q) a la proyección deq sobre P3 y L1 y L2 a las líneas que se obtienen cuando P3 corta a P1 y a P2 respectivamente. Es claro que L1 y L2 son líneas soporte de d1(q) y además la distancia entre ellas es precisamente la distancia entre P1 y P2. Como d1(q) es de ancho constante h, entonces la distancia entre L1 y L es h y por lo tanto el ancho de q en la dirección d es h. Si ahora escogemos cualquier otra dirección podemos argumentar igual para concluir también que en esta otra dirección el ancho de q es h, es decir, para concluir que el ancho de q en cualquier dirección es h.
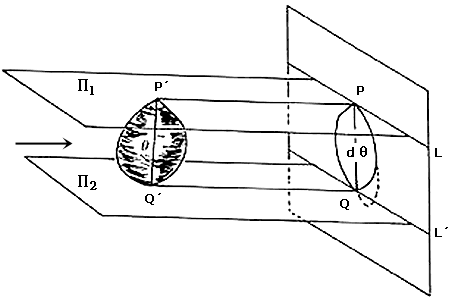
Supongamos ahora que q es un sólido de ancho constante h y que d(q) es la proyección de q en la dirección d sobre el plano P (ver figura VIII.3). Queremos demostrar que d(q) es una figura de ancho constante h. Para tal efecto bastará tomar una dirección cualquiera d1 en el plano P y ver que el ancho de d(q) en la dirección d1 es h. Pensemos en los planos y P1 y P2 en la dirección d que cortan a P en L1 y L2, respectivamente.
Vemos que P1 y P2 son planos soporte de q pues sus proyecciones en la dirección d son precisamente L1y L2. Como q es de ancho constante h y la distancia entre P1 y P2 es la misma que la distancia entre L1 y L2 tenemos que el ancho de d(q) en la dirección d1 es h. Es decir, d(q) es una figura de ancho constante h.
¿Será cierto que si todas las tajadas (secciones transversales) de un sólido son figuras de ancho constante, necesariamente el sólido es un sólido de ancho constante?
La respuesta es sí pero, como veremos más adelante, esta respuesta es más interesante que un simple sí. Por ahora, necesitamos una caracterización de los sólidos de ancho constante en términos de sus binormales.
Una cuerda de un sólido y es un segmento de línea contenido en y cuyos extremos están en la frontera de y. Una normal de un sólido y es una cuerda de y con la propiedad de que el plano perpendicular por uno de sus extremos es plano soporte de y. Finalmente, una binormal de un sólido y es una cuerda con la propiedad de que los planos perpendiculares por sus dos extremos son planos soporte de y. Por supuesto, en un sólido de ancho constante h, los conceptos de diámetro, binormal y cuerda de longitud h, coinciden.
Si en un sólido toda normal es binormal es porque el sólido es de ancho constante y viceversa; en un sólido de ancho constante toda normal es binormal.
Demostración. Supongamos que tenemos un sólido q con la propiedad de que todas sus normales son realmente binormales. Vamos a ver que si así es, entonces todas sus proyecciones son de ancho constante y por lo tanto, él mismo es de ancho constante. Tomemos d, una dirección cualquiera, y proyectemos a q en la dirección d sobre el plano P perpendicular a d. Llamemos d(q) a la proyección de q sobre P (ver figura VII.4). Vamos a comprobar que d(q) es de ancho constante probando que toda normal de d(q) es una binormal. Sea PQ una normal de d(q), es decir, PQ es una cuerda de d(q) y la línea L que se encuentra en P y es perpendicular a PQ por P es línea soporte de d(q). Sea P1 el plano paralelo a la dirección d que corta a P en la línea L. Es decir, P1 es el plano que, al proyectarse sobre P en la dirección d, deja a la línea L como sombra. Por supuesto P1, es un plano soporte de q y por tanto existe un punto P' en el que se proyecta sobre el punto P. Sea P'Q' la cuerda de q perpendicular a P1. La cuerda P'Q' es una normal de q y por lo tanto una binormal de q. Así, el plano P2 perpendicular a P'Q' por Q' , es un plano soporte de q. Por otro lado, el plano P2 corta a P en la línea L' que es una línea soporte de d(q) paralela a L —pues P1 y P2 son planos paralelos. Obviamente, la proyección de la cuerda P'Q' sobre P es la cuerda PQ de d(q). Por lo tanto, la línea soporte L' pasa por q, lo que muestra que PQ es realmente una binormal de d(q). Esto muestra que d(q) es una figura de ancho constante. Como toda proyección de q es de ancho constante, entonces q también lo es.
Supongamos ahora que q es un sólido de ancho
constante. Es posible convencerse de que toda normal de q
es una binormal repitiendo, palabra por palabra, la demostración de que lo mismo
sucede en las figuras de ancho constante![]()
Si toda sección transversal de un sólido Q es una figura de ancho constante es porque el sólido Q es una esfera.
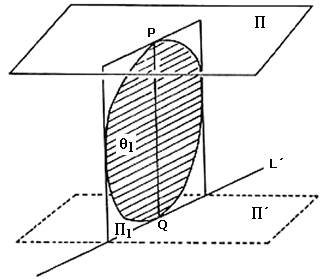
Demostración. Empezaremos demostrando que Q es un sólido de ancho constante, verificando que todas sus normales son en realidad binormales. Sea PQ una normal de Q y llamemos P al plano soporte de Q, perpendicular a PQ, que pasa por P (ver figura VII. 5). Necesitamos probar que el plano P' , perpendicular a PQ, que pasa por Q, es un plano soporte de Q. Pensemos en un plano cualquiera que pase por PQ. Escoja usted uno y llámelo P1. La sección transversal determinada por P1 es una figura de ancho constante, a la que llamaremos Q1. Claramente, PQ es una normal de Ql pues, si L es la línea en donde P corta a P1, entonces L es una línea soporte de Ql que pasa por P y es perpendicular a PQ. Como en una figura de ancho constante toda normal es binormal, entonces si L' es la línea en donde P' corta a P1, tenemos que L' es una línea soporte de Q1 que pasa por Q y es perpendicular a PQ. Como lo mismo pasa para cualquier plano que contenga a PQ entonces P 'es un plano soporte de Q, PQ es una binormal de Q, y Q es un sólido de ancho constante.
A continuación mostraremos que Q es realmente una esfera demostrando que todas las proyecciones de Q son círculos. Tomemos d, una dirección cualquiera, y llamemos P y P´ a los planos soporte de Q perpendiculares a la dirección d (ver figura VII.6). Como Q es un sólido de ancho constante, digamos h, entonces el plano P toca a Q en el punto K, el plano P' toca a Q en el punto T y K T es una cuerda de longitud h, perpendicular a P a P '. Sea y la proyección de Q en la dirección d, sobre el plano P. Usaremos el resultado principal del capítulo III para demostrar que y es un círculo. Tomemos un punto M de la frontera de y. Necesitamos comprobar que existe una línea soporte de y que pasa por M y es perpendicular al segmento de línea KM. Para esto será suficiente probar que la cuerda MN de y que pasa por K y por M es una binormal de y.
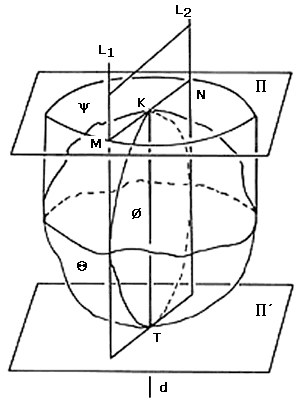
Tomemos ahora el plano P1 que
pasa por los puntos K, T, M y N, y llamemos f
a la figura de ancho constante h que se obtiene en P1
como sección transversal de Q. Las líneas
L1 y L2, paralelas a KT, que están
en P1 y pasan por M y por
N respectivamente, son líneas soporte de Q
por lo que la distancia entre ellas, es decir, la longitud del segmento MN,
es h. Luego entonces, MN es una cuerda de y
que tiene longitud h. Como y
es una figura de ancho constante, por ser proyección de un sólido de ancho constante,
MN es una binormal de y y por lo tanto,
por M pasa una línea soporte de y que
es perpendicular al segmento KM. Por el resultado principal del capítulo
III, y es un círculo. Finalmente, Q
es una esfera pues todas sus proyecciones son círculos. ![]()
Anora es claro, puesto que no todo sólido de ancho constante es una esfera, que no todas las tajadas de un sólido de ancho constante, distinto de una esfera, son figuras de ancho constante pero, entonces, ¿qué figuras pueden obtenerse como tajadas de un sólido de ancho constante? ¿Es posible que una figura convexa muy larga, por ejemplo con la forma de una lombriz ovalada, pueda obtenerse como tajada de un sólido de ancho constante?
La respuesta a la segunda pregunta es sí, siempre y cuando el sólido sea de un ancho suficientemente grande.