III. QU�TATE T� PARA PONERME YO. LA COMPETENCIA ENTRE ESPECIES
EL PUEBLO de Malinalco, en el Estado de M�xico, es muy conocido por su espectacular templo del dios del viento. Malinalco tambi�n tiene un convento agustino del siglo XVI, en cuyo claustro alg�n an�nimo artista ind�gena pint� unos interesant�simos murales. El tema de los murales no es b�blico ni religioso, sino profano y, a m�s abundamiento, naturalista. A primera vista, es dif�cil distinguir alg�n orden en las paredes blanquinegras y repletas de figuras y l�neas tan entrecruzadas que pudieran sugerir un ejercicio de caligraf�a ar�biga. Sin embargo, al acercarse, el orden subyacente se manifiesta. Vemos entonces un bosque formado por una gran variedad de plantas, estilizadas pero reconocibles, habitado por garzas, colibr�es, serpientes, coat�es, conejos, etc. Los animales se encuentran casi todos enfrascados en diferentes formas de lo que Darwin llam� "la lucha por la existencia": hay garzas devorando peces, serpientes a punto de atacar pajarillos, colibr�es y palomas visitando flores, y un par de coat�es arrebat�ndose la comida.
�Cu�l habr� sido el prop�sito religioso o did�ctico del mural? No s� si exista una respuesta a esta pregunta. Ser�a muy interesante averiguar los motivos que tuvieron los frailes agustinos del siglo XVI para encargar estos frescos. Y el artista (o artistas) ind�gena que los ejecut�, �por qu� raz�n habr� escogido los ejemplos particulares?
Cualesquiera que hayan sido las razones religiosas o art�sticas que expliquen el tema de los murales de Malinalco, desde mi punto de vista resultan particularmente interesantes porque en ellos est�n representadas las tres principales clases de interacciones entre dos especies: la competencia, la depredaci�n y el mutualismo (donde ambas especies se benefician). Habiendo analizado ya los tipos de interacciones que ocurren m�s com�nmente entre los miembros de una misma especie, iniciaremos ahora la descripci�n de lo que ocurre entre diferentes especies.
Los casos m�s simples, mejor entendidos te�ricamente y para los que se cuenta con una mayor cantidad de datos, son aquellos en los que intervienen preponderantemente s�lo dos especies. Ahora bien, en la naturaleza todas las interacciones son multiespec�ficas, hablando estrictamente. Sin embargo, como ya dijimos, est� justificado metodol�gicamente tratar de entender primero los fen�menos m�s simples y menos reales o comunes para pasar despu�s a los m�s complejos y usuales. Dicho metaf�ricamente, tratar�amos de interpretar todo lo que se pueda del mural en t�rminos de sus detalles. Lo global en t�rminos de lo local. Personalmente creo que este ejercicio reduccionista no puede llevarse a un extremo: las propiedades de una comunidad biol�gica en toda su complejidad no pueden deducirse de la mera suma de las interacciones entre pares de componentes. Sin embargo, es indispensable entender estas interacciones para el planteamiento general del problema de la ecolog�a de las interacciones multiespec�ficas. Por otro lado, los casos para los que contamos con m�s datos cuantitativos y una mejor comprensi�n de la historia natural descriptiva, son los de interacciones biespec�ficas.
En forma similar a la gr�fica que en el cap�tulo anterior representaba los tipos de interacciones entre individuos de una misma especie, se puede integrar otra que represente los resultados de las interacciones entre dos especies, tomando como criterio los resultados demogr�ficos de la interacci�n. Simbolizando con un + un aumento, con un - un decremento, y con 0 la ausencia de cambio en las tasas de crecimiento, tenemos: 1) la interacci�n resulta perjudicial para ambas especies (--); 2) beneficiosa para ambas (++); 3) beneficiosa para una y perjudicial para la otra (+-); 4) beneficiosa para una e indiferente para la otra (+0) y, por �ltimo, 5) perjudicial para una e indiferente para la otra (-0). Los tres primeros tipos de interacciones son aparentemente los m�s importantes y han sido bastante bien estudiados. Se denominan, por orden: competencia, mutualismo y relaci�n depredador-presa (lato sensu). Los dos �ltimos tipos (+0 y -0) incluyen algunas interacciones fascinantes desde el punto de vista de la historia natural (por ejemplo, las foresis, o relaciones de transporte, las cuales se ejemplifican en el libro de la doctora Ana Hofmann, de esta misma colecci�n). Sin embargo, su importancia en el desarrollo de la teor�a ecol�gica ha sido bastante menor, por lo que no se mencionar�n en lo sucesivo.
La primera clase de interacciones que analizaremos en este libro es la - -, es decir, las llamadas interacciones competitivas.
La interacci�n entre una especie A y otra B se llama competitiva cuando un aumento en los n�meros de A causa una ca�da en los n�meros de B y, de manera rec�proca, un incremento en B redunda en una ca�da en los de A. Estrictamente, esta disminuci�n en las tasas de crecimiento debe ser a causa de que la oferta de alg�n recurso com�n (espacio, comida, luz, etc.) sea limitada, por lo que, a altas densidades de poblaci�n, una cierta proporci�n de individuos de ambas especies queda siempre sin alcanzar una cantidad �ptima del recurso.
Es posible que la competencia por el recurso sea directa o incluso violenta; por ejemplo, la que se da entre ciertas abejas tropicales y los colibr�es que explotan las mismas flores. Las abejas persiguen activamente a los colibr�es y les impiden aprovechar el n�ctar. A este tipo de interacci�n se le denomina "competencia por interferencia". Por otra parte, la competencia puede darse sin que se establezca nunca un contacto f�sico directo. Pensemos otra vez en la competencia por el n�ctar de las flores. La sola presencia de una especie explotadora, al disminuir la cantidad de n�ctar, puede afectar a otra especie de explotador que visite las flores algo m�s tarde que la primera. Se da la interacci�n sin que los competidores se encuentren nunca juntos y se le llama "competencia por explotaci�n".
La teor�a de las interacciones competitivas fue de las primeras en desarrollarse en la ecolog�a moderna y tuvo una gran importancia en la conformaci�n actual de esta ciencia. En la d�cada de los veinte, un matem�tico italiano, Vito Volterra, y un biof�sico norteamericano, Alfred Lotka, propusieron independientemente las ecuaciones conocidas en la actualidad como modelos de Lotka-Volterra. No obstante ser esquem�ticamente simples, dichas ecuaciones catalizaron de manera notable la actividad de muchos ec�logos. Algunos se lanzaron, casi febrilmente, a demostrar en el laboratorio o en el campo que las ecuaciones eran "correctas , mientras que otros m�s, claramente irritados por la brusca intromisi�n de matem�ticos en los dominios de la historia natural, intentaron con la misma dedicaci�n demostrar que las ecuaciones eran "incorrectas". Un tercer grupo se concentr� en desarrollar te�ricamente las implicaciones de las ecuaciones o en buscarles alternativas. Poco a poco, fue asent�ndose la idea de que la importancia de tales modelos simplificados no radicaba en su "veracidad" o "falsedad"; que su papel no era predecir o describir con exactitud los fen�menos ecol�gicos, sino m�s bien dar un contexto conceptual y sugerir las hip�tesis de trabajo que guiaran la investigaci�n emp�rica. Durante mucho tiempo, la investigaci�n en ecolog�a de poblaciones y comunidades (sobre todo en los pa�ses anglosajones) estuvo permeada por la noci�n de que la competencia era la interacci�n de mayor importancia en la estructura de las comunidades. Estudios posteriores han hecho hincapi� menor en la competencia, aunque �sta sigue siendo la interacci�n preferida de una influyente escuela de ec�logos de comunidades.
A continuaci�n presentaremos los fundamentos de la teor�a de la competencia y posteriormente la ilustraremos con datos de laboratorio y de campo.
En el cap�tulo anterior se facilitaba el planteamiento de las ecuaciones de
crecimiento poblacional suponiendo un crecimiento en generaciones discretas
o separadas. Sin embargo, a partir del presente cap�tulo resulta m�s simple
suponer que las especies crecen continuamente: esto es, que los nacimientos
y muertes ocurren a lo largo de todo el a�o, sincr�nicamente. Si aceptamos esto,
as� como algunas otras premisas que se analizar�n despu�s, se pueden plantear
las siguientes relaciones:
| Tasa de crecimiento del competidor A |
|
Tasa de crecimiento del competidor A en ausencia del competidor B |
|
Tasa de mortalidad producida por el competidor B |
| Tasa de crecimiento del competidor B |
|
Tasa de crecimiento del competidor B en ausencia del competidor A |
|
Tasa de mortalidad producida por el competidor A |
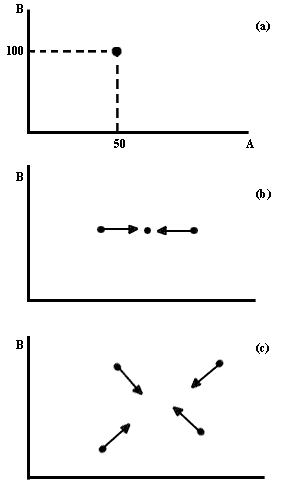
Figura III.1. Representaci�n de los cambios poblacionales mediante el espacio
de fase.
Al llegar a este punto deberemos abrir un par�ntesis para describir la herramienta de an�lisis que aplicaremos al estudio de estas relaciones, y las correspondientes a los cap�tulos posteriores. En esencia, se trata de la representaci�n geom�trica del sistema mediante lo que se conoce como espacio de fase. La idea es simple y elegante: en un plano representamos a la densidad poblacional de la especie A como distancias medidas en el sentido horizontal, y a la especie B como distancias medidas en un sentido vertical (Figura III.1a). Cualquier combinaci�n concebible de especies corresponde a alg�n punto en el plano. As�, el origen corresponde a la ausencia de A y B; el eje de las X a cualquier densidad de A en ausencia de B, etc�tera.
Supongamos que para una combinaci�n dada de A y B, por ejemplo 50 y 100 (v�ase la figura III.la), calculamos el tama�o de la tasa de crecimiento de la especie A (usando una ecuaci�n como la planteada arriba). Esta tasa de crecimiento puede representarse como una flecha sohre la l�nea horizontal que pasa por el punto 50, 100. En caso de que la tasa de crecimiento sea positiva (la poblaci�n tienda a crecer), convendremos en apuntar la flecha hacia la derecha; si la tasa es negativa, la flecha apuntar� hacia la izquierda; y si la tasa es de cero (esto representa una poblaci�n en equilibrio) entonces no hay flecha (v�ase la figura III.lb). Lo propio se puede hacer para la especie B, con la diferencia de que las flechas se encuentran ahora sobre l�neas verticales. Tenemos entonces representadas en un plano geom�trico no s�lo todas las posibles combinaciones de las dos especies, sino tambi�n la tendencia demogr�fica de cada una. Podemos resumir la informaci�n usando una sola flecha para cada punto, en lugar de dos, si aceptamos que la longitud de cada flecha sea proporcional al tama�o de la tasa de cambio en ese punto. La "suma vectorial" de ambas flechas, llamada la resultante, puede tener cualquier direcci�n (ya no s�lo vertical y horizontal) y representa la direcci�n hacia la que tender�a a moverse el punto que representa a una combinaci�n dada (Figura III. lc). Nuestra representaci�n geom�trica adquiere entonces una dimensi�n din�mica que antes no ten�a: si conocemos la "topograf�a" de las flechitas, podremos visualizar hacia d�nde se mover� cualquier punto que pudiera ser de inter�s.
Por razones matem�ticas que tienen que ver, entre otras suposiciones, con la de que el cambio en las poblaciones es continuo y no se da por generaciones separadas, "la topograf�a" del espacio de las flechitas resulta simple y regular. El plano se encuentra dividido en regiones dentro de las cuales la direcci�n general de las flechas es la misma. Esto es, dentro de una misma regi�n no es posible encontrar flechas que apunten, por ejemplo, en direcciones opuestas. Hay que cambiar de regi�n para encontrar cambios cualitativos en la direcci�n de las flechitas. Los tipos de regiones son pocos: 1) regiones donde ambas poblaciones crecen; 2) donde ambas decrecen; 3) donde una crece y la otra decrece, y 4) donde una o ambas se encuentran estacionarias. Las primeras tres son, en general, �reas, mientras que en la cuarta categor�a encontramos las l�neas o puntos que sirven de fronteras a las regiones de los primeros tres tipos. La colocaci�n, tama�o y forma de cada posible regi�n est�n determinados por los detalles biol�gicos de la interacci�n que se est� modelando. En particular, a los tres tipos b�sicos de interacci�n entre dos especies (++, +- y - -) corresponden tambi�n tres tipos b�sicos, cualitativamente distintos, de disposici�n de las regiones mencionadas. El lector que haya seguido la argumentaci�n hasta el final estar� en condiciones de comprender la teor�a b�sica de las interacciones entre dos especies.
Una vez cerrado el par�ntesis regresemos a la competencia interespec�fica.
En general, las ecuaciones que nos sirven para representar la competencia entre
dos especies diferentes corresponden a un espacio de fase del estilo del que
aparece en la figura III.2a. Las l�neas (llamadas "isoclinas cero") corresponden
a las combinaciones de competidores que permitir�an que cada especie se mantuviera
con una densidad estacionaria. Dicho en otras palabras, a lo largo de la l�nea
correspondiente a la especie A, �sta se encuentra en equilibrio, aunque B no
necesariamente se halle igual y viceversa. Si existe un punto en el que las
dos isoclinas se cruzan, �ste corresponde a la combinaci�n de densidades donde
ambas especies estar�an en equilibrio al mismo tiempo. El caso m�s simple es
aquel en el cual no hay intersecciones. En la figura III.2b se indica la topograf�a
de las regiones de flechitas.
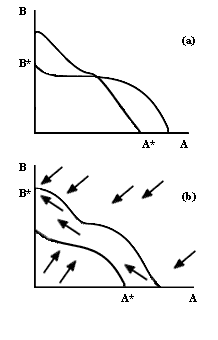
Figura III.2 Isoclinas cero para un sistema competitivo (a), y espacio de
fase de un sistema competitivo con exclusi�n de la especie A (b).
Resulta claro que desde cualquier punto (esto es, combinaci�n inicial de especies) en que se empiece, la comunidad se desplazar� poco a poco hacia un punto sobre el eje de la especie B que corresponde a la desaparici�n de la especie A, a lo cual se le llama exclusi�n competitiva. Si la isoclina de A es la que se encuentra por arriba, la excluida resultar�a la especie B. La topograf�a detallada del espacio de flechas se obtiene a partir de la forma espec�fica de las ecuaciones correspondientes a cada sistema. Aunque el procedimiento no es complicado, no se presentar� aqu�. El texto de Begon, Harper y Townsend es una excelente obra de consulta para obtener m�s detalles al respecto.
Ahora bien, en el caso de que las isoclinas se intersecten en un punto, pueden
darse dos posibilidades, ilustradas en la figura III.3: a) Se excluye
una u otra de las especies, dependiendo de la combinacion inicial, o b) ambas
especies de competidores coexisten indefinidamente. Tenemos entonces tres casos
donde hay exclusi�n y uno donde se puede dar la coexistencia. Biol�gicamente
hablando, para que ocurra la coexistencia es necesario que la tasa de crecimiento
de la especie A sea positiva cuando A es muy poco abundante y B est� en su tama�o
m�ximo en ausencia de competidores, y viceversa. En t�rminos gr�ficos, se requiere
que en la cercan�a de los puntos A* y B* de la figura III.3b, tanto la flechita
de B como la de A, respectivamente, se dirijan hacia adentro del plano, y ninguna
hacia afuera.
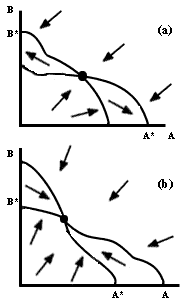
Figura III.3. Espacios de fase que corresponden a exclusi�n dependiente
de la poblaci�n inicial (a), y coexistencia. (b).
La teor�a de la competencia, delineada aqu�, sugiere que en un sistema con dos competidores hay una tendencia a la exclusi�n de uno de ellos, y con ella se indican las condiciones precisas para que se d� la coexistencia. Ahora bien, no es posible, tanto por razones pr�cticas como fundamentales, obtener las ecuaciones "exactas" de la competencia entre dos especies antes de realizar el experimento. En efecto, no existen unas ecuaciones exactas de la competencia, pues como ha sido demostrado en estudios de laboratorio muy detallados, el modo mismo (los par�metros o incluso la forma de las ecuaciones) de competir va cambiando con cada generaci�n, de tal suerte que no es posible predecir con exactitud el resultado de una interacci�n competitiva con base en las ecuaciones de Lotka-Volterra. Por lo tanto, la predicci�n resultante de la teor�a de la competencia parecer�a reducirse, como Hutchinson ha hecho notar, a la frase vac�a "dos especies que compiten, o coexisten o no lo hacen". La teor�a de la competencia resultar�a ser, m�s que nada, una clasificaci�n de los posibles resultados de la interacci�n.
Sin embargo, la imagen anterior es injusta. Contar con una teor�a permiti� a los ec�logos encuadrar sus observaciones dentro de un marco conceptual. La b�squeda de "confirmaciones" o "refutaciones" de la teor�a se convirti� pronto en mucho m�s que una mera lista de ejemplos y contraejemplos: se clasificaron grandes grupos de organismos por su tendencia a competir usualmente o no; se inici� el estudio de los mecanismos biol�gicos que promueven la coexistencia; se desarroll� la hip�tesis de que la competencia era la principal determinante del n�mero de especies que pod�an vivir juntas en una comunidad; la necesidad de realizar las precisas observaciones requeridas por la teor�a llev� a afinar y desarrollar la metodolog�a experimental en la ecolog�a de campo, etc. Teor�a y observaciones se estimularon mutuamente, en un juego que inclu�a al mismo tiempo refutaciones y confirmaciones, est�mulo a la imaginaci�n y su desaliento, todo dentro de una ortodoxia en la que se consideraba un poco her�tico suponer que la competencia no fuera la interacci�n biol�gica por excelencia.
Esta fruct�fera influencia rec�proca entre teor�a y pr�ctica se inici� cuando en la d�cada de los treinta, inspirado por las ecuaciones de Lotka-Volterra, el bi�logo ruso G. F. Gause realiz� experimentos de laboratorio con dos especies de protozoarios, en las que observ� la exclusi�n en algunos casos y la coexistencia en otros. A los experimentos de Gause les sucedieron otros en los que se utilizaban gorgojos (insectos que se alimentan de granos) y en los cuales, dependiendo de las condiciones de temperatura, se obten�a la exclusi�n de una u otra especie. Estos experimentos (junto con las ecuaciones de Lotka-Volterra) se utilizaron para dar apoyo a lo que despu�s se denomin� "principio de exclusi�n competitiva", que durante un corto tiempo goz� del dudoso privilegio de ser considerado el dogma de la ecolog�a de poblaciones: "dos especies suficientemente parecidas no pueden coexistir en la naturaleza". Por "suficientemente parecidas" se entiende que utilizan los mismos recursos en forma similar. Los naturalistas, sin embargo, conoc�an un buen n�mero de contraejemplos al principio de exclusi�n competitiva. El debate subsecuente parec�a separar por un lado a te�ricos y experimentalistas y por otro a naturalistas, pero muy pronto un grupo de naturalistas especializados en ecolog�a de aves y roedores comenz� a tomar partido a favor de la validez del principio de exclusi�n. Para la d�cada de los cincuenta parec�a haberse llegado a un impasse, con los ec�logos de poblaciones divididos en dos grandes escuelas: la que consideraba que los fen�menos de regulaci�n dependientes de la densidad eran fundamentales en el funcionamiento de las poblaciones, y los que pensaban que las poblaciones no estaban reguladas y que el principio de exclusi�n competitiva era un concepto que carec�a de contenido emp�rico.
A mediados de los cincuenta, George Evelyn Hutchinson y su alumno de doctorado, Robert MacArthur, presentaron un notable avance te�rico, seguido por un extraordinario estudio de campo, lo que prest� nuevos �mpetus a los estudios sobre la competencia. Dicho avance consisti� en la formalizaci�n de la teor�a del nicho ecol�gico. Hutchinson present� en t�rminos matem�ticos la vieja idea de que los organismos, al ocupar un determinado espacio f�sico, al estar activos a horas definidas del d�a, al utilizar ciertos recursos con preferencia a otros, etc., definen un cierto "nicho", propio de cada especie o poblaci�n; la competencia se da dentro de las partes en com�n de los nichos de diferentes especies. Posteriormente, MacArthur reformul� los coeficientes de las ecuaciones de Lotka-Volterra en t�rminos de esta idea.
El trabajo de campo, la tesis doctoral de MacArthur, consisti� en aplicar a un sistema natural las ideas anteriores. El autor estudi� uno compuesto por varias especies de warblers (cerrojillos o reinitas), pajarillos residentes en un bosque de Nueva Inglaterra. Las cinco especies de reinitas son sumamente parecidas y es necesaria cierta experiencia en la observaci�n de aves para distinguirlas en el campo. M�s a�n, era bien sabido que las cinco especies se alimentaban de insectos, y como los bosques de abetos en Maine y Vermont son bastante homog�neos, el caso de las reinitas podr�a considerarse como un magn�fico ejemplo de especies cercanas que no se exclu�an, esto es, constitu�an una contradicci�n al "dogma" de la exclusi�n competitiva.
MacArthur invirti� mucho tiempo en la observaci�n y en el estudio de las actividades de las reinitas, as� como de la zona de los �rboles donde transcurr�an �stas. Uno de los m�s importantes resultados de este estudio fue la demostraci�n de que cada una de las cinco especies pasa la mayor parte de su tiempo en diferentes zonas del �rbol (v�ase la figura III.4). Dicho en otras palabras: MacArthur logr� demostrar que, aunque aparentemente las reinitas en Nueva Inglaterra ocupaban el mismo nicho (silv�colas, diurnas, insect�voras), en realidad un estudio m�s fino revelaba importantes diferencias en su forma de explotar los insectos del bosque, y por ende los nichos de las especies resultaban diferentes. La consecuencia es que, al no ser suficientemente parecidas desde un punto de vista ecol�gico las diferentes especies de reinitas no constituyen verdaderos competidores entre s�.
La idea de que para que dos especies sean competidoras deben tener nichos sobrepuestos,
junto con la demostraci�n de que las diferencias en los nichos pueden ser muy
sutiles y dif�ciles de observar, estimularon una sucesi�n de estudios de campo
en donde se pretend�a explicar la coexistencia de especies cercanas mediante
el descubrimiento de inevitables diferencias en sus nichos.
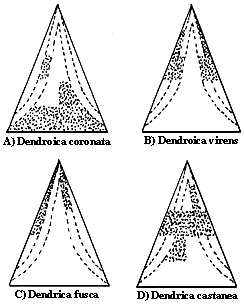
Figura III.4. Segregaci�n del uso de h�bitat en las "reinitas" estudiadas
por R. H. MacArthur.
As�, diferencias en los tama�os de los picos de aves gran�voras, en las profundidades a las que los peces depredadores buscan a sus presas, en los periodos de floraci�n de las plantas, etc., se propusieron como pruebas de la acci�n de la competencia, recurriendo al argumento: "estas especies son diferentes porque si no lo fueran ya alguna habr�a sido excluida". Sin embargo, este argumento no es susceptible de falsificaci�n, es decir, no se puede dise�ar, ni en principio, una observaci�n que llegue a refutar el argumento anterior porque: 1) no es posible especificar ni medir el grado de diferencia que se requerir�a para que tuviera que presentarse la exclusi�n, y 2) el ec�logo no tiene acceso a informaci�n cuantitativa sobre la historia pasada de las especies que actualmente coexisten, ni sobre la de aquellas que ya no lo hacen. Siendo infalsificable, dicho argumento es sugestivo y motivador, pero de dudosa utilidad directa.
Conforme m�s ec�logos se percataban de lo anterior, a las observaciones de gran detalle se empezaron a a�adir experimentos de campo. B�sicamente se intentaba, mediante manipulaci�n artificial de las densidades de las especies en supuesta competencia, demostrar que los signos de las tasas de cambio eran ambos negativos. Por ejemplo, en un experimento realizado con lagartijas del g�nero Anolis, se dividi� el �rea en varias parcelas. En algunas se retir� a la especie A de Anolis, en otras a la especie B, y en otras se mantuvieron las dos, para tener un control experimental. Si se demostraba (como en efecto ocurri�) que la ausencia de A ten�a un efecto positivo en la tasa de crecimiento de B, y viceversa, se presentar�a un fuerte argumento en favor de la existencia de una interacci�n competitiva y entonces ser�a posible interpretar con mucho mayor rigor las observaciones de historia natural que documentaban diferencias de nicho.
Aunque los experimentos de campo en esta �rea no son ninguna novedad (Darwin realiz� algunos cl�sicos), s� es cierto que empezaron a hacerse comunes a partir de la d�cada de los sesenta, con un predominio de los realizados con plantas, no s�lo porque muchas plantas son sujetos experimentales m�s sencillos que los animales, sino porque se contaba con la experiencia de los agr�nomos, quienes por largo tiempo hab�an realizado experimentos semejantes a aquellos que los ec�logos comenzaban a intentar.
Los experimentos de campo del ec�logo moderno son, en su mayor�a, muy dif�ciles de realizar. Se requieren dise�os experimentales con un fundamento estad�stico a veces muy complicado, y la puesta en pr�ctica del experimento suele implicar muchos d�as de trabajo duro y rutinario, marcando, contando, rastreando y midiendo organismos que nunca cooperan con el experimentador. Adem�s, como el control que el ec�logo tiene sobre una serie de variables importantes (por ejemplo, el clima), es nulo o muy limitado, los resultados de los experimentos rara vez admiten una explicaci�n inequ�voca. Sin embargo, junto con m�todos cuantitativos en la observaci�n de la historia natural de los organismos, los experimentos le han dado a la ecolog�a de poblaciones de campo un alto grado de rigor.
El ya largo periodo (m�s de sesenta a�os) de desarrollo te�rico-experimental de la noci�n de la competencia interespec�fica, ha tenido consecuencias de gran importancia para la ciencia de la ecolog�a. Hemos marcado la relevancia de algunas de las consecuencias de tipo metodol�gico: una m�s correcta apreciaci�n del papel de los modelos te�ricos, no tanto como herramientas productivas sino heur�sticas, as� como el desarrollo de un grado mucho mayor de refinamiento en el trabajo emp�rico, tanto experimental como observacional. Mencionaremos ahora algunos de los principales resultados generales que podemos aceptar como v�lidos, dada la situaci�n actual de desarrollo de la ecolog�a.
En primer lugar, parece claro que hay grandes grupos de organismos para los cuales la competencia interespec�fica rara vez resulta ser una interacci�n importante. Un ejemplo de lo anterior son los insectos herb�voros, sobre todo en climas templados o con estaciones muy marcadas. Para ilustrar esto podemos referirnos al estudio de las comunidades de insectos asociadas al helecho Pteridium aquilinum. Esta asociaci�n ha sido estudiada por John Lawton en Inglaterra y Hawai y Colorado EUA, y ha sido imposible demostrar la presencia de competencia interespec�fica, ni directa ni indirectamente. Existen ejemplos similares en otras comunidades de insectos.
Por otra parte, en muchas poblaciones de vertebrados, como en aves, peque�os roedores, lagartijas, etc., la competencia interespec�fica se ha demostrado en forma experimental. Similarmente, no hay duda de que entre muchas especies de plantas se presenta una a veces muy aguda competencia por recursos tales como la luz, el agua, o micrositios adecuados para germinar. Joseph Connell, en 1982, analiz� 527 experimentos de campo reportados en la bibliograf�a por diferentes autores. Para casi la mitad de las especies estudiadas, y en un 40% de los experimentos realizados, se pudo demostrar la presencia de interacciones competitivas. De modo que es indudable que existe la competencia, aunque su importancia relativa a�n se cuestiona.
�Cu�les son las consecuencias de la competencia interespec�fica para aquellas especies o tipos de especies en las que se presenta? En primer lugar, la competencia, al ser una presi�n selectiva, tiene consecuencias adaptativas directas para aquellas especies que han evolucionado bajo su influencia. Las diferencias ("segregaci�n") en los nichos de especies competidoras son a menudo atribuidas a los efectos de la competencia. Por ejemplo, cuando dos especies de ciertos ratones habitan el mismo sitio, sus tama�os promedio no se superponen. Esto es, una especie es algo menor en tama�o que la otra. En �reas diferentes, donde las mismas especies no coexisten, los tama�os promedio son aproximadamente iguales. Se explica la observaci�n anterior como un resultado de la competencia que ha promovido la especializaci�n en semillas m�s peque�as por una especie y m�s grandes por la otra, para evitar esta interacci�n competitiva en aquellas regiones en que ambas especies viven juntas.
De manera similar, la competencia afecta las �reas de distribuci�n de los organismos competidores, de tal forma que especies cercanas o de ecolog�a muy parecida deben de coexistir geogr�ficamente mucho menos a menudo que especies muy distintas. David Lack ha demostrado que tal es el caso para un buen n�mero de grupos de aves de todo el mundo. Sin embargo, deber�an encontrarse excepciones a la regla anterior en medios ambientes complejos, en donde se presentan posibilidades de subdividir el h�bitat en diferentes zonas, o los recursos en diferentes partes, segregando los nichos, como se mencion� anteriormente.
En segundo lugar, la competencia puede inducir importantes similitudes en grupos completos de organismos en diferentes partes del mundo. Por ejemplo, James Brown ha estudiado diversas comunidades de roedores en el desierto sonorense. En sitios similares clim�tica y topogr�ficamente, las comunidades convergen hasta un grado sorprendente. Tanto el n�mero de especies, como sus tama�os y la forma de utilizar los recursos son muy parecidos de un sitio a otro, pese a que las especies son diferentes en los distintos sitios. Algo muy semejante ha sido reportado por Martin Cody en las comunidades de aves de los chaparrales californianos y los matorrales chilenos: pese a la enorme distancia y la composici�n totalmente diferente de especies, la estructura de las comunidades (el n�mero de especies, sus tama�os, la sobreposici�n de nichos, etc.), en ambas localidades es muy parecida.
En resumen, el estudio de las interacciones competitivas en la ecolog�a de poblaciones ha tenido una gran importancia te�rica, y aunque en la actualidad resulta muy claro que la competencia no es un fen�meno tan extendido, ni sus consecuencias son tan importantes como se pensaba hace pocos a�os, tampoco hay duda de que en ciertos sistemas y grupos biol�gicos constituye una interacci�n de gran relevancia y capaz de proporcionar cierta estructura a las comunidades.
