II. MEJOR SOLOS QUE MAL ACOMPAñADOS. CRECIMIENTO DE UNA SOLA ESPECIE
| Sed fecundos y multiplicaos, y henchid la Tierra y someterla. Génesis 1,28 |
UNO de los principios básicos del quehacer del científico es que se deben entender y resolver primero los problemas sencillos para luego pasar a los más complicados. Ahora bien, las interacciones de los seres vivos entre sí y con su medio forman una complejísima red, siempre cambiante, siempre dinámica, cuya trama oculta apenas se empieza a conocer. Aunque los naturalistas clásicos habían descrito desde hace mucho tiempo notables casos de interacciones entre varias especies, sólo hasta principios del siglo presente se empieza a desarrollar una teoría matemática de las interacciones. En este capítulo iniciaremos la descripción y análisis del crecimiento poblacional de una sola especie en términos de las cuatro causas básicas de cambio numérico (nacimientos, muertes, inmigración y emigración) y de los factores que las afectan.
Los ecólogos resumen la información de las causas del cambio en las llamadas tablas de vida. Esencialmente, la tabla de vida no es más que un registro de las muertes y los nacimientos en las diferentes categorías de edad (o de tamaño, o estadio) de una población. Por ejemplo, una mariposa pasa por los estadios de huevo, cinco fases larvales, una de crisálida y la de adulto. Una tabla de vida para esta mariposa es un recuento de la cantidad de huevecillos que sobreviven de la puesta original; después, de cuántas larvas de cada estadio, cuántas crisálidas y finalmente cuántos adultos, hasta la muerte del último. Además, se incluye la información de los huevecillos depositados por los adultos. En el caso del ser humano, las tablas de vida se dividen en grupos de edades, generalmente de 5 en 5 años. Hay diferentes técnicas para estimar las probabilidades de que un individuo que entra a un grupo cualquiera de edades pase al siguiente, así como la fecundidad promedio de los individuos de cada uno de estos grupos.
La importancia de las tablas de vida radica en que además de ser un resumen de los nacimientos y muertes de un grupo de organismos, permiten calcular parámetros tan importantes como la tasa de crecimiento de la población, su estructura de edades "final" o estable, y otros de la mayor importancia para el demógrafo. Los detalles técnicos del cálculo de los valores de la tabla, así como de los parámetros derivados de ella, varían para poblaciones con generaciones separadas o con generaciones superpuestas. Este libro no es el lugar adecuado para analizar apropiadamente las técnicas demográficas que se utilizan en los diferentes tipos de tablas de vida, por lo que, sin entrar en los detalles de la obtención de los parámetros del crecimiento de las poblaciones a partir de las tablas, mostraremos los principales aspectos dinámicos de dicho crecimiento.
Tal vez la manera más simple de imaginar el crecimiento de una población sea
considerando aquellas que tienen generaciones separadas. Este es un caso extremo
dentro de una amplia gama de posibilidades. En sitios donde el clima es marcadamente
estacional (con inviernos muy crudos o temporadas anuales sumamente secas) es
muy común encontrar que los organismos vivos se reproducen durante una temporada
relativamente reducida del año, y que los adultos mueren pasada la temporada
reproductiva. En contraste, en otras especies o poblaciones los adultos permanecen
reproductivos por varias estaciones e incluso existen casos en los que no hay
estaciones reproductivas (como ocurre en la especie humana). Imaginando el primer
caso, esto es, donde se presentan estaciones reproductivas seguidas de mortalidad
de todos los adultos, es posible plantear la siguiente relación:
|
|
|
|
|
|
|
|
Si consideramos diferentes tipos de poblaciones, la relación anterior variaría en sus detalles, pero no en su esencia. Suponiendo otra vez una población aislada, con el fin de ignorar la migración, podemos notar que el número de juveniles producidos por adulto, multiplicado por la tasa de supervivencia, es el factor clave que determina si la población crece, se mantiene estacionaria o decrece. A este producto se le llama tasa de reproducción per capita. Si dicha tasa es mayor que la unidad, entonces cada adulto está siendo reemplazado en la siguiente generación por más de un adulto (en promedio). Si el producto fuera exactamente igual a uno (lo cual es muy improbable en la realidad) entonces cada adulto sería remplazado por otro, con un crecimiento neto poblacional de cero. Si, por último, el producto fuera menor que uno, la población decrecería, puesto que en el balance final algunos adultos quedarían sin remplazo. En el apéndice se describen simulaciones sencillas que ayudarán a comprender este punto, y en la figura II. 1 se ilustra el resultado de cada caso.
En la mayoría de las poblaciones reales la tasa per capita es fluctuante, ya que la disponibilidad y calidad de los recursos, la variabilidad climática y la acción de otras especies rara vez permiten mantener constantes la fecundidad o la probabilidad de sobrevivir.
Desde un punto de vista meramente numérico, lo único importante es el valor
neto del producto fecundidad X sobrevivencia. Por ejemplo, muchas especies de
peces producen miles o millones de huevecillos, de los cuales sobreviven muy
pocos, apenas los necesarios para equilibrar en el largo plazo las pérdidas
y las ganancias; dicho en otras palabras, los necesarios para mantener en promedio
un producto fecundidad X sobrevivencia cercano a uno. Existen en cambio otras
especies, por ejemplo de aves, que producen muy pocos juveniles por adulto (dos
o tres), pero cuya tasa de supervivencia es tan alta, cercana al 100%, que el
efecto numérico es el mismo, esto es, un balance en el largo plazo entre pérdidas
y ganancias. Sin embargo, desde otros puntos de vista, ecológicos y evolutivos,
es radicalmente diferente producir gran número de juveniles cuyas tasas de supervivencia
sean bajísimas, a producir muy pocos pero con mucho mejores perspectivas. Por
desgracia, este tema de tan grande interés se sale de las posibilidades del
presente libro.
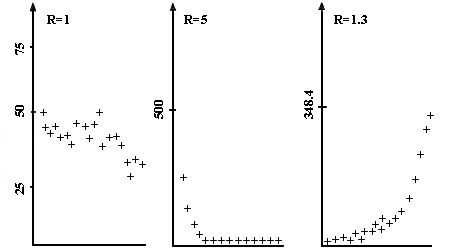
Figura II.1. Crecimientos exponenciales con tasa mayor de la 1 (a); tasa
de la 1 (b); y tasa menor de 1 (c). Simulaciones realizadas con el "frijolarium"
descrito en el apéndice y parámetros R = 1.3, 1 y 0.5.
El primer autor importante que analizó los problemas del crecimiento poblacional fue Malthus. Argumentando que la población humana crecía en forma geométrica, mientras que los alimentos sólo lo harían en forma aritmética, profetizó un negro futuro para la humanidad. El crecimiento geométrico de Malthus no es más que un crecimiento con una tasa per capita constante y mayor que uno. Las explosivas posibilidades de una ley de crecimiento exponencial no son siempre bien apreciadas. Consideremos el caso humilde de la bacteria Escherichia coli, un conspicuo miembro de nuestra flora intestinal. De forma ligeramente oblonga, esta bacteria no tiene más de una centésima de milímetro de largo y en condiciones ideales se puede reproducir (duplicar) una vez cada veinte minutos. Ahora bien, si ninguna de las bacterias hijas muriera, los descendientes de un solo ejemplar producirían una masa del volumen de la Tierra en ñ36 horas! Éste es un caso hipotético. En la naturaleza rara vez se presentan ejemplos de crecimiento exponencial sostenido por intervalos largos de tiempo; sin embargo, estos casos no son ni desconocidos ni irrelevantes. En Australia, por ejemplo, una especie de nopal fue introducida en 1839 y para 1920 ya había cubierto una extensión de 24 millones de hectáreas, que así resultaban completamente inútiles para la agricultura. Un caso similar padecieron los australianos después de la introducción de conejos: a su importación en 1865 siguió una fase de crecimiento exponencial que para 1950 había producido un estimado de 300 millones de animalitos. Ambas plagas pudieron ser controladas gracias a la introducción de enemigos naturales o controles biológicos, fenómeno que se analizará en capítulos posteriores.
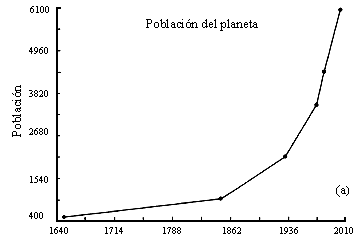
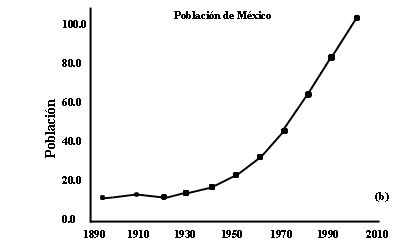
Otro caso de crecimiento explosivo es el de la población humana. En las figuras
II.2a y II.2b se presentan datos del tamaño de la población mundial y la de
México. Puede observarse claramente que a periodos largos de un crecimiento
muy lento sigue la fase actual de crecimiento acelerado. En el caso de la población
humana la ley de crecimiento es incluso más rápida que la exponencial, ya que
la tasa per capita no es constante, sino que aumenta, sobre todo a causa
de cambios sociales y tecnológicos que han hecho disminuir las tasas de mortalidad
en muchos países. Aunque la humanidad ha pasado antes por fases de crecimiento
rápido, nunca se había encontrado en una de la magnitud absoluta y relativa
de la presente.
|
|
Figura II.2. Crecimiento poblacional del mundo (a) y de México (b). Datos
proporcionados por el Consejo Nacional de Población (CONAPO), y
de Paul Ehrlich, en The Population Bomb. La extrapolación del año 2000
se obtiene suponiendo que no hay cambios en las tasas de crecimiento.
En ningún caso es posible mantener un crecimiento exponencial por tiempo indefinido.
Tarde o temprano la fecundidad o la sobrevivencia per capita (o ambas)
disminuirán debido a uno o varios factores: puede ocurrir que algún recurso
(comida, espacio, etc.) se haga muy escaso debido a la demanda de una población
muy grande. Puede también suceder que las aglomeraciones favorezcan la rápida
dispersión de enfermedades (epidemias o epizootias) o bien atraigan a los depredadores.
También es posible que se presenten cambios conductuales (canibalismo, homosexualidad)
que redunden en una tasa de crecimiento per capita menor. Todos los factores
mencionados se han documentado tanto en el ser humano como en plantas o animales;
sin embargo, el caso de la especie humana es cualitativamente distinto debido
a nuestras particularidades sociales y culturales. Aunque es imposible negar
(o temer) la acción de algunos de estos mecanismos de regulación meramente biológicos
en nuestra especie, cualquier apreciación seria de la demografía humana debe
de explicitar un contexto histórico e integrar nuestra condición de seres sociales
y culturales.
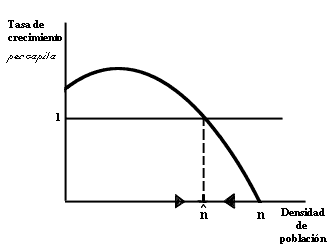
Figura II.3. Cambios densodependientes en la tasa de crecimiento por cabeza
(R). Al aumentar mucho la densidad poblacional (N) se produce una disminución
de R como consecuencia de la competencia por alimento u otros recursos,
la acción más intensa de patógenos o depredadores, el deterioro del medio, etc.
A una cierta densidad N, la tasa R vale 1 y al población está en equilibrio.
Resulta entonces que la tasa de crecimiento per capita no puede permanecer
constante de manera indefinida y por arriba del valor de remplazo igual a uno.
A partir de alguna densidad de población y en forma más o menos suave, dependiendo
de la especie y sus condiciones, la tasa per capita disminuirá por abajo
de uno. A esto se le llama regulación del crecimiento poblacional. En
la figura II.3 se ilustra la idea: el eje vertical (eje de las ordenadas) nos
sirve para representar la tasa de crecimiento per capita, y el eje horizontal,
la densidad de la población. La gráfica representa la tasa correspondiente a
una densidad cualquiera. Si recordamos que una tasa mayor que uno quiere decir
un crecimiento de la población, y una tasa menor que uno decrecimiento, entonces
es fácil ver que la región por encima de la línea horizontal (que representa
una tasa de 1) corresponde a crecimiento de la población, mientras que la región
por abajo de dicha línea indica decrecimiento. La densidad de la población 
,
correspondiente al punto donde se cruzan las dos líneas, constituye la población
de equilibrio. Teóricamente, una población de exactamente
individuos permanecería siempre del mismo tamaño, ya que su tasa de crecimiento
es de uno. Sin embargo, existen numerosos factores aleatorios que pueden apartar
a la población de su valor .
Ahora bien, si por cualquier causa el tamaño de la población se hace mayor que
, entonces nos habremos
movido a la derecha en la figura II.3 y la tasa de crecimiento se hace menor
que uno, lo cual implica una tendencia a disminuir y moverse a la izquierda.
Si lo contrario ocurre, esto es, la población se desplaza a la izquierda de
, entonces la tasa per
capita se hace mayor que uno y tiende a compensar y a desplazar a la población
hacia la derecha. Este mecanismo puede resultar lo mismo en una regulación muy
fina y suave de la población en el equilibrio, que en fluctuaciones muy bruscas
alrededor de éste. La figura II.4 muestras dos ejemplos extremos. Uno, de regulación
suave, en una mariposa tropical en el campo, y el otro, de fluctuaciones abruptas,
en una palomilla que es plaga de los pinos. En el Apéndice se encuentran las
simulaciones correspondientes a ambos casos.
Resulta interesante mencionar que es muy fácil, en teoría, demostrar casos en los que la regulación poblacional no conduce a un régimen de estabilidad o "equilibrio", sino por el contrario, a fluctuaciones sumamente irregulares, denominadas caóticas, las cuales difícilmente pueden distinguirse de una serie de cambios debidos al azar. Algunos estudios recientes parecen indicar que las dinámicas de ciertas enfermedades, así como las de algunas plagas agrícolas, son ejemplos de este extraño azar, paradójicamente derivado del determinismo más estricto. En el Apéndice se describe la simulación correspondiente.
|
|
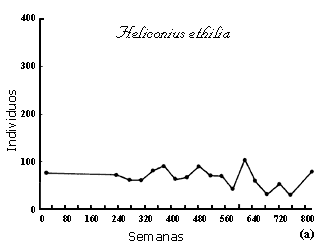
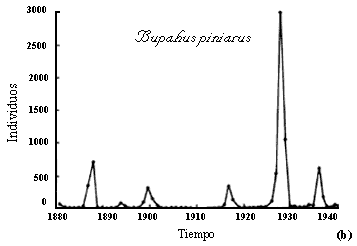
Figura II.4. Ejemplos de una población natural en equilibrio (a), y otra
sujeta a fluctuaciones violentas (b). Datos tomados de Ehrlich, P. Y L. Gilbert
(1973) Biotrópica 5(2):69-82 y Schwerdtfeger, A., en G. Varley (1949)
J. An. Ecol. 18: 117-122.
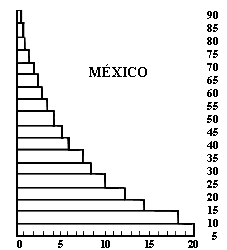
Figura II.5. Estructura de edades de la población de la República Mexicana.
Datos del CONAPO.
La variedad de ciclos de vida de plantas y animales no puede ser representada por un solo tipo de ecuación de crecimiento. Existe un buen número de modelos matemáticos de crecimiento de población que dan preponderancia a diferentes aspectos del ciclo de vida de los organismos. Por ejemplo, la llamada estructura de edades es esencial para entender el crecimiento de muchísimas especies, entre ellas la humana. Es fácil ver esto. Si bruscamente, de hoy a mañana, todas las parejas mexicanas decidieran tener sólo dos hijos (o sea uno por cabeza), la población del país seguiría creciendo por un tiempo debido al enorme número de parejas en edad prerreproductiva que en los años futuros contribuirán al crecimiento. La estructura de edades de México, típica de los países subdesarrollados (véase la figura II.5), contiene a una enorme población de jóvenes cuyo número compensara con creces (por algunos años) cualquier disminución de la tasa per capita de crecimiento. Por el contrario, en otros países, el escaso número de prerreproductivos implica que, aun con tasas de crecimiento per capita mayores que uno, la población disminuirá por algún tiempo, para finalmente alcanzar el equilibrio.
Otro factor que complica el análisis teórico del crecimiento poblacional es que las fecundidades y las sobrevivencias no son las mismas de un sitio a otro de los ocupados por una misma población; es decir que las ecuaciones de crecimiento son a menudo una especie de promedio que abstrae la diversidad natural. Esto es obvio en el caso del hombre (la mortalidad infantil no es igual en las zonas más ricas de la ciudad de México que en la Mixteca oaxaqueña) y no menos cierto en el caso de plantas y animales. Esta variabilidad puede alcanzar extremos casi increíbles, como en ciertas especies de áfidos para los cuales no sólo no es igual chupar de hojas jóvenes o viejas, sino que dentro de una misma hoja una diferencia de pocos milímetros en el sitio de succión puede ser decisivo para sobrevivir o morir. Tal variabilidad local en la tasa de crecimiento per capita no puede simplemente promediarse para obtener una ecuación global. Los resultados teóricos que se obtienen al calcular una tasa promedio son muy diferentes de aquéllos obtenidos al "promediar", en un cierto sentido, muchas ecuaciones separadas, una para cada localidad.
Las complicaciones derivadas de introducir la estructura de edades, la heterogeneidad medioambiental u otras, no pueden ser analizadas en detalle aquí. Mencionaremos únicamente las conclusiones generales, válidas para la mayoría de las poblaciones, que se pueden deducir de los modelos matemáticos menos detallados y de los experimentos y observaciones de campo:
1. Cuando la tasa de crecimiento per capita de una población es constante, dicha población crece exponencialmente (crecimiento "geométrico" de Malthus) cuando la tasa es mayor de uno, o permanece sin cambios (la población se encuentra en equilibrio) cuando la tasa es uno, o bien decae paulatinamente hasta su extinción, si la tasa es menor que uno. 2. Es infrecuente, pero no imposible, encontrar que las tasas de crecimiento per capita permanezcan constantes por periodos largos de tiempo. Ejemplos importantes son las invasiones de nuevas regiones por especies que en ellas carecen de enemigos naturales, como los ejemplos de los nopales o los conejos en Australia; en estos casos se presenta un crecimiento exponencial. Los casos de equilibrio (tasa per capita = 1) se encuentran más frecuentemente en medios ambientes con muy pequeñas fluctuaciones ambientales, como las selvas tropicales siempre verdes, las cuevas, etc. Por último, la extinción local de muchas poblaciones ha sido bien documentada. 3. Pese a que es posible que la tasa de crecimiento per capita permanezca constante, lo normal es que sufra fluctuaciones, incluso algunas muy severas. Dichas fluctuaciones pueden ser independientes del tamaño de la población o dependientes de éste. En el primer caso, las fluctuaciones pueden deberse a los cambios climáticos, a la acción de cierto tipo de enemigos naturales que no se especializan en el organismo en cuestión, y en general a todo tipo de factores aleatorios (caída de meteoritos, apertura de una carretera, inundaciones, etcétera). A estos cambios en la tasa de crecimiento corresponden cambios en el tamaño de la población, los cuales pueden ser de magnitud considerable, pero no están regulados. En el segundo caso, los cambios en la tasa per capita correlacionados con cambios en la densidad de la población pueden regular el tamaño de la misma, según vimos anteriormente. En la naturaleza se presentan todas las posibilidades, incluso diferentes poblaciones de la misma especie pueden ser reguladas de diversas formas, o carecer de todo tipo de regulación. |
Desde un punto de vista puramente numérico, la causa de la muerte de un individuo resulta irrelevante. El individuo desaparece de la contabilidad y basta. De manera similar, la naturaleza de las causas por las que un organismo fracasa al intentar reproducirse no afecta el valor de una tasa de crecimiento per capita determinada. Lo importante, desde un punto de vista estrictamente demográfico, son los valores de los números y no sus causas. Sin embargo, como ya se señaló anteriormente, entre los seres vivos el "quién" importa tanto como el "cuántos". Más aún, en el largo plazo, el "quién" y el "cuántos" son dos caras de la misma moneda. Al ecólogo de poblaciones le resulta de particular importancia, y fascinante, describir y entender cuántos y quiénes mueren debido a sus encuentros e interacciones con otros organismos vivos. En términos de los resultados netos, existen tres tipos de interacciones: las que benefician a un individuo, las que lo dañan y las que le resultan indiferentes. Esta división lógica y exhaustiva encubre una compleja gama de posibilidades biológicas que, siendo muy distintas en cuanto a mecanismos, generan los mismos resultados demográficos. Mencionaremos ahora algunas de las que se presentan entre organismos de la misma especie.
Cuando dos individuos interactúan, los resultados de la interacción pueden
representarse en la siguiente gráfica:
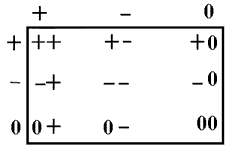
El signo + representa un resultado beneficioso; el -, uno perjudicial, y el 0, un resultado indiferente. Un ++ entonces significa que ambos individuos se benefician de la interacción; un +-, que uno se beneficia y el otro resulta perjudicado, etc. Los beneficios o perjuicios se miden en unidades de tasa reproductiva, esto es, hablamos de beneficios o daños demográficos.
La primera clase de interacciones que analizaremos es la de tipo --. El tipo de interacción -- es a menudo responsable de los incrementos en la mortalidad (o disminución de la natalidad) asociados con altas densidades de población. Cuando, por ejemplo, el alimento escasea en un área, la presencia de un nuevo individuo afecta negativamente a otros potenciales consumidores del mismo alimento, ya que éste deberá repartirse entre más individuos. Al fenómeno de utilizar recursos escasos se le llama competencia y, en el caso de que se dé entre individuos de la misma especie, competencia intraespecífica.
La competencia asume muchas formas. Puede ser directa o indirecta, violenta y agresiva o sutil y refinada. Puede terminar con la muerte de uno de los competidores, en su depauperación o en su infertilidad. Consideremos, por ejemplo, el amable caso de algunas flores y sus polinizadores. Muchas especies de plantas requieren para su reproducción de poner en contacto el polen de un individuo masculino con los óvulos de un individuo femenino. Para ello es bastante frecuente que sea necesaria la presencia de un intermediario, el polinizador, el cual transporta el polen entre las diferentes flores. Ahora bien, no siempre ocurre que haya suficientes polinizadores para la cantidad de plantas en alguna localidad. Se establece entonces una competencia entre las flores masculinas por los polinizadores disponibles, o, planteado en términos evolutivos, la selección natural favorece a aquellas plantas cuyas flores atraen mejor a los polinizadores. Existen formas "honestas" de atraer a los polinizadores, tales como ofrecer más o mejor néctar, sacrificar una parte del polen (que es muy rico en proteínas) para alimentar al polinizador, proveerse de una arquitectura floral que facilite al polinizador el acceso a su recompensa, etc. Existe, por otra parte, toda una serie de seducciones "deshonestas" (por ejemplo, presentar flores olorosas y atractivas, pero carentes de néctar) de las que hablaremos en un capítulo posterior. El punto esencial que hay que dejar claro es que aquellas flores masculinas que por cualquier mecanismo heredable logren las visitas de un número relativamente mayor de polinizadores, transmitirán esta característica a sus descendientes, con el resultado de que aquellas especies de plantas que habitualmente, a lo largo de muchas generaciones, hayan sufrido escasez de polinizadores, deberán presentar adaptaciones relacionadas con su atracción, como producción de néctar, flores vistosas, etc. Sin embargo, las especies que no compitan por sus polinizadores no tienen por qué presentar tales adaptaciones. Tal es el caso de las especies polinizadas por elementos físicos del ambiente, como viento o agua, las cuales no tendrían ventaja selectiva al presentar las características atractoras mencionadas antes.
En otros casos, la competencia puede ser más directa y violenta. Muchas aves, por ejemplo, pelean por las parejas o por sitios privilegiados para anidar, o incluso por los territorios donde se realizan los bailes o los cortejos de apareamiento. Los alegres gorjeos matinales de los pájaros parecen tener el prosaico objeto de restablecer los territorios para obtener sus alimentos cada nuevo día. Entre los mamíferos también son comunes las peleas por la pareja, y muchos peces presentan este mismo tipo de conducta. Los machos de los "betas" (Betta splendens), peces ornamentales muy conocidos por los acuaristas, deben ser mantenidos separados para evitar las peleas a muerte.
Menos conocido es el hecho de que entre los insectos también se da la lucha por parejas por territorios de apareamiento. Algunas frágiles mariposas entablan feroces combates cuando un macho entra en el territorio de otro. A veces esta conducta parece llevar al macho demasiado lejos. En efecto, no es raro observar a una mariposa territorial atacando y persiguiendo a cualquier "objeto volador no identificado" que penetre en su territorio, como otras especies de insectos, aves e incluso piedras arrojadas.
Es posible que el recurso por el cual los individuos de todas las especies compiten con más frecuencia sea la comida, ya directamente, como dos palomas por un grano de trigo, o indirectamente, como dos abejas por el néctar repartido en las plantas de un campo. Los recursos alimenticios son casi siempre insuficientes para satisfacer las necesidades de las poblaciones que los explotan. En las aves, por ejemplo, los padres suelen proveer a sus polluelos de alimento; es muy común que la comida no sea suficiente para todos ellos, lo cual se manifiesta, por una parte, en los gritos, píos y actitudes con los que los polluelos exigen a sus padres una mayor eficiencia, y por otra, en los múltiples casos de fratricidio, medio por el cual los polluelos dominantes se desembarazan de algunos competidores.
Incluso cuando en términos absolutos el recurso es perfectamente suficiente, el modo de su explotación puede convertirlo en escaso. Las plantas, por ejemplo, se nutren de algunas sales minerales, agua, aire y luz. Alrededor de un 0.2% de toda la luz solar que llega a la Tierra se utiliza en la fotosíntesis. Sin embargo, no es aventurado afirmar que la gran mayoría de las plantas compiten con otras por la luz. Los individuos altos sombrean a los más pequeños, los adultos a los jóvenes, etc. En las selvas altas tropicales esta competencia se vuelve muy intensa. En el suelo de una selva sin perturbar (de las pocas que quedan sobre nuestro planeta) se encuentra un gran número de plántulas esperando la oportunidad para crecer. En cualquier momento, una rama o un árbol completo puede caer, arrastrando consigo a muchos otros y abriendo así un claro en la penumbra del bosque. La luz, recurso escaso en el suelo de la selva, se convierte de pronto en abundante y las plántulas latentes inician una carrera por levantarse antes de que el claro se cierre de nuevo y la sombra retorne al lugar. Rápidamente, inclusive dentro de plántulas de la misma especie, aquellas que llevan ventaja en tamaño, lugar, etc., empiezan a sombrear a sus vecinas amplificando así las diferencias de tamaño. En cualquier plantación densa de vegetales de la misma especie, al cabo de un tiempo se tienen unos cuantos individuos dominantes y un mayor número de individuos "supresos", según la terminología botánica: los que obtuvieron los peores lugares en su competencia por la luz.
Hemos mencionado la competencia por alimento, por parejas, por territorios y por polinizadores. Existe además un recurso poco estudiado, pero aparentemente de gran importancia, por el cual compiten muchas especies vivas. Se le ha denominado el "espacio libre de enemigos", y en esencia es cualquier región del medio dentro de la cual es poco probable ser víctima de los ataques de depredadores, parásitos, etc. Muchos depredadores son capaces de identificar los sitios de alta densidad de presas y de concentrar sus actividades en ellos. Resulta entonces que los lugares donde dicha densidad es baja están relativamente protegidos de los depredadores. Estos sitios de baja densidad de presas se convierten en un recurso por el cual se puede competir. La visita de nuevos individuos de la especie al sitio lo deteriora, simplemente por hacerlo más atractivo a los depredadores. La presencia de cada individuo se convierte en perjudicial para sus vecinos.
Como un ejemplo, consideremos el caso de los ectoparásitos (pulgas, garrapatas, moscas, etc.) del ganado: la acción de una o dos moscas puede ser insuficiente para estimular la respuesta defensiva, digamos de un caballo (arrugar la piel, dar un coletazo, rascarse contra un poste, etc.), pero si muchas moscas se congregan sobre el mismo sitio el estímulo será lo suficientemente intenso como para que el caballo se defienda. Las moscas compiten entre sí por el espacio de piel de caballo que está libre de la respuesta defensiva.
La competencia intraespecífica generalmente se presenta o se intensifica cuando la densidad de las poblaciones es alta. Como los resultados demográficos de la competencia son siempre, por definición, incrementos en la mortalidad o decrementos en la natalidad per capita, la competencia intraespecífica es un agente regulador de gran importancia. La acción de enemigos naturales acoplados, el otro gran agente de regulación poblacional, se analizará en un capítulo posterior.
Hablaremos ahora un poco de las interacciones de tipo +-, esto es, aquellas en las cuales uno de los participantes se beneficia mientras que el otro resulta perjudicado. Este tipo de interacción es menos claro y definido que el anterior, por lo que nos limitaremos a presentar un par de ejemplos.
El mejor ejemplo de este tipo de interacción es el canibalismo. Mucho más extendido en la naturaleza de lo que podría pensarse (se presenta entre mamíferos, reptiles, aves, peces, insectos, arañas, etc.), resulta obviamente perjudicial para uno de los participantes y beneficioso para el otro. Dada la extendida (y errónea) creencia de que la evolución actúa "para el bien de la especie", no faltará quien se extrañe de que una práctica tan lamentable como el canibalismo no haya sido extirpada por la selección natural. Recordemos, sin embargo, que la selección natural actúa fundamentalmente en los niveles del individuo y del gene. Un caníbal, al alimentarse mejor que otros individuos de su misma población, puede muy bien dejar más descendencia que los otros y por lo tanto incluso ser seleccionado. Lo anterior puede suceder siempre y cuando el caníbal no tenga preferencia sobre su propia descendencia, en cuyo caso la selección natural operaría en contra de tal característica.
Otro ejemplo muy ilustrativo de interacciones +- lo encontramos en el infanticidio en las manadas de leones. Es común entre primates y roedores que los machos que se integran a un grupo maten a los jóvenes o infantes que puedan. En el caso de los leones, tal y como ha sido estudiado en Tanzania, los grupos sociales constan de varias hembras, su progenie, y una coalición de machos que se aparean con las hembras del grupo. Las coaliciones de machos compiten por los grupos de hembras, y frecuentemente se da el caso de que una coalición de machos sea sustituida por otra. La mortalidad infantil se incrementa bruscamente durante las sustituciones. Se ha observado que los nuevos machos atacan y matan a los cachorros, o bien los echan del grupo, pese a la vigorosa oposición de las leonas, las cuales pueden incluso salir heridas al defender a su progenie. Ahora bien, es claro que los cachorros no se benefician con la presencia de los nuevos amos del hogar, pero ¿qué ganan éstos con su conducta poco caritativa? Consideremos la pregunta desde un punto de vista evolutivo: supongamos que la propensión al infanticidio fuera heredable, esto es, que los hijos de leones infanticidas tendieran a seguir las costumbres de sus padres. Una coalición de leones infanticidas, después de una sustitución, no pierde ni el tiempo ni las energías de sus recién adquiridas hembras en el cuidado de cachorros ajenos. Se excluye a éstos y se procede a generar nuevas camadas de leoncitos que, por hipótesis, tendrán las tendencias infanticidas paternales. En cambio, una coalición de leones "tolerantes", que permitiera a las hembras culminar la larga crianza de los cachorros ajenos antes de aparearse, corre el riesgo de nunca llegar a procrear. Las hembras pueden morir o envejecer, otra coalición puede sustituirlos, un mal año puede sobrevenir trayendo la muerte de los cachorros propios, etc. En resumen, la característica conductual heredable de ser infanticida de cachorros ajenos tiene altas probabilidades de proliferar dentro de las poblaciones de leones. La ganancia de los machos infanticidas es evolutiva, a largo plazo, y estrictamente hablando quienes ganan no son los machos en cuestión, sino los genes responsables de su conducta.
Las interacciones ++ dentro de una misma especie se reducen básicamente a las relaciones sexuales y a los intercambios sociales denominados "altruistas".
Las relaciones sexuales benefician a ambos participantes porque la esencia misma de lo vivo consiste en dejar descendencia. Este es el premio último y mayor. La esterilidad es un fracaso ontológico. En aquellas especies (la mayoría) en las que predomina la reproducción sexual, se requieren generalmente dos participantes para llevar a término el ciclo reproductivo, de ahí que ambos miembros de la pareja se beneficien, en un sentido evolutivo. Ahora bien, como ya hemos dicho varias veces, la selección natural opera fundamentalmente sobre genes o individuos. Cualquier característica heredable de un individuo que le permita dejar más descendencia tenderá a difundirse en las poblaciones futuras, independientemente de que perjudique a su pareja. Entonces el canibalismo sexual de muchos insectos beneficia a las hembras, quienes después de la cópula reciben una cantidad adicional de proteínas si consiguen devorar al macho. El macho, como tal, no se beneficia de ser devorado, pero tal vez sus genes sí. Esto depende básicamente del balance entre el número de copias de sus genes difundido por una hembra muy bien alimentada (gracias al sacrificio del padre) en relación con el número de copias que se obtengan de lograr fecundar a varias hembras no tan bien nutridas. Sin embargo, demasiadas variables intervienen en el proceso como para poder especular sobre bases sólidas, y en este punto dejaremos el tema.
Desde la perspectiva de la selección individual, las relaciones sexuales presentan varios aspectos fascinantes. En gran cantidad de especies la hembra invierte mucha más energía y tiempo en la preñez y cuidado de la progenie que el macho, cuya participación puede ser muy efímera. Una consecuencia de esto sería la tendencia a la irresponsabilidad y a la poligamia presente en los machos de muchas especies. En efecto, ¿para qué interesarse en el cuidado de la progenie tenida con una hembra cuando es igual o más fácil producir más progenie con otras? Se ha hipotetizado que la explicación de las complicadas pautas de cortejo existentes en muchas especies de aves radica en que así la hembra obliga al macho a invertir energía y tiempo antes de decidirse a procrear. Subsecuentes sesiones de cortejo resultan más caras y riesgosas (uno puede ser rechazado, con la consiguiente pérdida de tiempo y energías) que "quedarse en casa y ayudar a mamá a cuidar a los pequeños". Otra vez, la selección de la estrategia dependerá de un balance: el número de genes difundidos como consecuencia de ayudar al cuidado, y por ende promover el éxito de una sola camada vs. el número de genes difundidos como resultado de producir varias camadas menos exitosas. Ambas estrategias extremas se presentan en la naturaleza, lo cual no debe extrañarnos, ya que la conveniencia evolutiva de una u otra depende de muchos factores cambiantes.
El tema de la selección sexual es suficientemente amplio como para ocupar varios libros, por lo que no podemos profundizar en él. Pasaremos entonces a ejemplificar las relaciones llamadas altruistas, que son otro caso importante de interacción ++.
Las interacciones altruistas son a menudo tipificadas con la frase "si tú me rascas la espalda, yo te la rasco a ti". Se presentan más a menudo en los organismos llamados superiores (aves, mamíferos), y están basadas en el hecho evolutivo de que puede ser benéfico para los genes de un individuo invertir un poco de esfuerzo (vía el fenotipo) en un plazo inmediato, a cambio de recibir beneficios (esto es, difundir sus copias) a mediano y largo plazo.
Por ejemplo, consideremos el caso estudiado por Packer, y relatado por Maynard-Smith, de los babuinos en la reserva nacional de Gombe, en Tanzania. A menudo ocurre que un macho que está en conflicto con otro por alguna causa (por ejemplo, por una hembra), solicita la ayuda de un tercero. En aproximadamente un 25% de los casos, el macho que solicitó la ayuda obtiene a la hembra. Ahora bien, ¿qué ganó el macho que fue a ayudar? El primero tiene la posibilidad de difundir sus genes, y al original poseedor de la hembra se le despojó de esta posibilidad. Pero el segundo macho no parece beneficiarse demográficamente de su conducta. Una hipótesis para explicar este comportamiento es que el macho ayudante esperará ayuda futura del macho a quien ayudó en el presente. Obviamente, de aparecer "tramposos" que soliciten ayuda pero no la den al llegar su turno, deberían de ser identificados por los otros y sus solicitudes rechazadas. Los datos de Packer apoyan esta conclusión. Parece que existe una tendencia a establecer relaciones de ayuda, en las que hay un alto grado de reciprocidad.
Para que este mecanismo funcione se requiere que los organismos sean capaces de distinguir a unos individuos de otros, lo cual no tiene por qué hacerse conscientemente. Un gran número de claves, tales como olores, colores, e incluso rasgos faciales, pueden ser asociadas, en forma puramente refleja, con la posibilidad de recibir la ayuda.
En este capítulo hemos visto que bajo condiciones que permitan mantener la tasa de crecimiento constante, una población crece exponencialmente (crecimiento geométrico de Malthus) o bien decrece hasta la extinción. También vimos que existen diversas interacciones entre los individuos de una misma especie que pueden hacer variar la tasa de crecimiento. Las variaciones en la tasa de crecimiento tienen consecuencias dinámicas (por ejemplo, regulación del tamaño de la población, oscilaciones, etc.) y consecuencias evolutivas.
Existe un gran número de semejanzas entre lo que ocurre en poblaciones de animales y lo que ocurre con el ser humano. Algunas semejanzas son reales, tanto en el plano demográfico como en el evolutivo. Otras, en cambio, son meramente superficiales. En tiempos recientes se ha hecho un intento muy serio por explicar un gran número de fenómenos sociales y culturales propiamente humanos en términos de genética y dinámica de poblaciones. A esta escuela de pensamiento se le llama "sociobiología" (existe también, por supuesto, sociobiología animal e incluso vegetal), debido al título de la obra pionera de E.O. Wilson, su principal exponente. Este tema se sale de los límites del libro, pero debido a la enorme importancia política que ha adquirido, es necesario mencionar algunos de sus puntos esenciales.
Los sociobiólogos humanos adoptan un punto de vista netamente reduccionista con respecto a la sociedad. Esto es, pretenden explicar y predecir los fenómenos sociales y culturales en términos de otros fenómenos de más bajo nivel, aquellos que ocurren en el ámbito de la naturaleza biológica y genética del ser humano. Por ejemplo, se postula un origen genético para el miedo a las arañas o a las serpientes, o para el gusto por los grandes jardines arbolados. Ahora bien, puede o no existir un gene para el miedo a las arañas, y el interés por su existencia es principalmente académico. Sin embargo, algunos sociobiólogos se han aventurado en terrenos menos seguros, presentando hipótesis y teorías cuya carga emocional y política va mucho más allá de lo meramente académico. En efecto, el origen genético de las desigualdades sociales entre hombres y mujeres, de la homosexualidad y de la superioridad" de ciertas razas ha sido discutido por los socio-biólogos y adoptado entusiastamente por los partidarios de un buen número de organizaciones de extrema derecha. Se debe de tener claro que la explicación genética de este tipo de caracteres sociales humanos es, a lo sumo, hipotética. Por otra parte, incluso si existiera la base genética para explicar condiciones como la homosexualidad, es muy simplista suponer que con ésta ya se explicó el proNema en términos biológicos. Los contextos social, cultural y político desempeñan un papel central en el entendimiento de este tipo de situaciones. No hay que tener miedo a buscar las bases biológicas de la conducta humana, pero creer que tales bases nos proveerán de una explicación global, o peor aún, de una "ética de los genes", como se ha propuesto alguna vez, resulta, para decirlo eufemísticamente, ingenuo, y puede ser francamente peligroso.
