III. LA METROLOG�A �PTICA

LA METROLOG�A �ptica es la rama de la �ptica que tiene como prop�sito efectuar medidas de muy alta precisi�n usando las ondas de la luz como escala. Esto se hace por medio de unos instrumentos llamados interfer�metros, basados en el fen�meno de la interferencia, que se describir� m�s adelante. Ya que dicha aplicaci�n est� fundamentada en la naturaleza ondulatoria de la luz, se comenzar� por describir brevemente la historia del desarrollo de los conceptos sobre la naturaleza de la luz. Posteriormente, se tratar�n las principales aplicaciones de la metrolog�a �ptica.

III.1. LA NATURALEZA DE LA LUZ

La naturaleza de la luz ha sido un enigma muy atractivo e interesante para los hombres, desde la m�s remota antig�edad. Los griegos pitag�ricos, alrededor de 530 a.C., al igual que Arist�teles doscientos a�os m�s tarde, cre�an que la visi�n era causada por part�culas que emit�a el cuerpo luminoso, que llegaban despu�s al ojo. Sin embargo, los fil�sofos Plat�n, Euclides y Claudio Tolomeo, cre�an que era justo lo contrario, es decir, que las part�culas sal�an del ojo para llegar despu�s al objeto observado. Alhazen, en Arabia, estaba convencido de que el punto de vista de Arist�teles era el correcto, es decir, que la luz sal�a de los objetos y que al penetrar en el ojo produc�a la sensaci�n visual. Sin embargo, no se hac�a todav�a ninguna conjetura sobre la naturaleza de estas emanaciones de las fuentes luminosas.

La primera suposici�n m�s o menos razonada se hizo durante la Edad Media, en el sentido de que la luz era un flujo de part�culas de naturaleza desconocida. Newton pens� con muy buenos argumentos cient�ficos, adecuados a su tiempo, que la luz estaba formada por corp�sculos de diferentes tama�os y velocidades, los que induc�an vibraciones en el medio en el cual se propagaba la luz, al que se llamaba �ter, de acuerdo con su tama�o y velocidad. Sin embargo, siempre le qued� la duda de si la luz era en realidad una part�cula o una onda, pues conoc�a los fen�menos de la difracci�n y de la doble refracci�n, que no pod�a explicar. Estas ideas fueron mal interpretadas en su tiempo, pues se crey� que Newton postulaba sin sombra de duda una teor�a completamente corpuscular. La gran autoridad que Newton ejerci� tanto sobre sus colegas como sobre sus sucesores, unida a la influencia de esta mala interpretaci�n, fue tan grande que aun cient�ficos tan importantes como sir David Brewster se opusieron rotundamente a la teor�a ondulatoria. Parad�jicamente, como veremos m�s adelante, Brewster realiz� estudios muy importantes sobre la polarizaci�n de la luz.

Francesco Maria Grimaldi (1618-1663) ingres� a la Compa��a de Jes�s a la edad de catorce a�os. En 1648, siendo ya jesuita, se le ofreci� la c�tedra de matem�ticas en Bolonia. En un experimento que realizo ah�, dej� que penetrara la luz del Sol a un cuarto obscuro a trav�s de un peque�o agujero en una cartulina (Figura 11). Hizo despu�s pasar esta luz a trav�s de otra cartulina perforada, con dimensiones que midi� muy cuidadosamente. Descubri� que la luz proyectaba una mancha mayor que la esperada si la propagaci�n de la luz fuera rectil�nea. En algunos otros experimentos observ� que la orilla de la sombra en lugar de estar bien definida, mostraba algunas franjas claras y oscuras, como se muestra en la figura 12. Estos fen�menos los atribuy� Grimaldi a la presencia de la difracci�n, debida a la naturaleza ondulatoria de la luz.

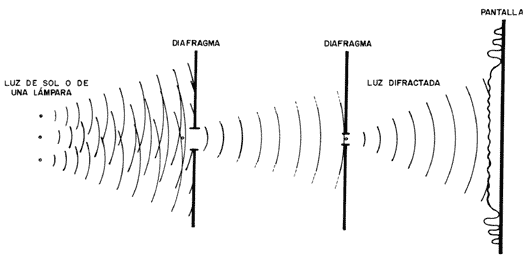
Figura 11. Experimento que muestra el fen�meno de la difracci�n.

Erasmo Bartholinus (1625-1692), un naturalista dan�s, descubri� en 1670 el fen�meno de la doble refracci�n en la calcita, llamada tambi�n espato de Islandia, observando que un rayo incidente se refracta en dos, a los que llam� rayo ordinario y rayo extraordinario, como se muestra en la figura 18. Sin embargo, no pudo encontrar una explicaci�n razonable de este fen�meno.

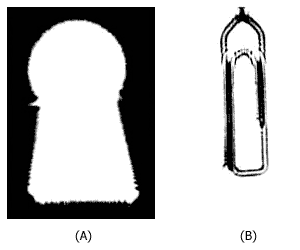
Figura 12. Im�genes de difracci�n de algunos objetos. (a) ojo de una llave de cerradura y (b) clip para papel.

Christian Huygens (1629-1695) naci� en La Haya, Holanda. Con la ayuda de su hermano y su amigo, el fil�sofo Baruch Spinoza, hizo estudios �pticos y astron�micos muy importantes. Fue el primero en identificar la aureola que vio Galileo alrededor de Saturno, como un anillo. En 1678, Huygens postul� que la luz era de naturaleza ondulatoria, es decir, que era como una onda. A fin de explicar la birrefringencia, supuso que el rayo ordinario correspond�a a una onda esf�rica, mientras que el extraordinario correspond�a a una onda esferoidal oblata, es decir, con la forma de una esfera achatada. Esta es la explicaci�n correcta; sin embargo, no convenci� a nadie debido a que cometi� el error de suponer que la luz era una onda longitudinal como el sonido, es decir, que la vibraci�n ocurr�a en la misma direcci�n de la propagaci�n de la onda. Con ayuda de su teor�a, Huygens explic� la reflexi�n, la refracci�n, la interferencia y la difracci�n, aunque s�lo en forma cualitativa.

Figura 13. Fen�meno de la birrefringencia en calcita.

Robert Hooke (1635-1703) era ayudante de Robert Boyle cuando en 1665 descubri� el fen�meno de la interferencia, al observar los brillantes colores de las pompas de jab�n y las pel�culas de aceite en agua. Hooke interpret� correctamente s�lo en forma parcial sus observaciones, las que relacion� indirectamente con movimientos ondulatorios longitudinales.

Hooke propuso que la luz se propagaba en ondas transversales, introduciendo as� el concepto de polarizaci�n de la luz. Ya con el concepto de polarizaci�n se pod�a explicar la doble refracci�n, pero no se ve�a en este tiempo c�mo era posible esto. Fue Etienne-Louis Malus quien en Par�s en 1775 resolvi� el enigma, con sus m�ltiples observaciones de fen�menos relacionados con la luz polarizada.

Thomas Young (1773-1829), m�dico de profesi�n y arque�logo de gran �xito, describi� en 1801 en Inglaterra algunos experimentos, entre los cuales el m�s importantes era el de la doble rendija. Con este experimento Young trataba de hacer resurgir la teor�a ondulatoria, que ya casi se hab�a olvidado por entonces. La vida de Young es tan interesante, que vale la pena relatarla aunque sea muy brevemente. Naci� en Milverton, Inglaterra, el 13 de junio de 1773. Thomas era un ni�o tan precoz que a la edad de dos a�os ya le�a con cierta fluidez. Antes de cumplir los cuatro a�os ya hab�a le�do dos veces el Antiguo Testamento de la Biblia. Durante su infancia aprendi� lat�n, italiano, franc�s, cir�lico, hebreo y algunos otros idiomas asi�ticos. Sus habilidades manuales tambi�n eran considerables, pues a los catorce a�os ya manejaba el torno, hac�a telescopios peque�os y encuadernaba libros. A los 17 a�os ya hab�a le�do los Principia y el Optics de Isaac Newton. Lo convencieron de que deb�a estudiar medicina, y termin� su carrera con �xito en 1799. Adem�s de practicar su profesi�n, decidi� hacer investigaciones sobre el ojo humano, lo que lo llev� a descubrir el astigmatismo y a inventar un opt�metro para medir los defectos de refracci�n del ojo.

Poco m�s tarde comenz� a realizar investigaciones sobre la visi�n en color, postulando que la visi�n de los colores es debida a que en el ojo existen tres tipos diferentes de receptores, cada uno de ellos sensible a un color diferente: rojo, amarillo o azul, a los que llam� colores primarios. Como sabemos, esta teor�a ha permanecido vigente con pocas modificaciones hasta nuestros d�as.

En 1801 Young hizo su famoso experimento de la doble rendija, con lo que demostr� la existencia de la interferencia de la luz. Con ello, Young se inici� como uno de los principales defensores de la teor�a ondulatoria de la luz.

Por aquellos a�os, las tropas francesas descubrieron durante el transcurso de unas excavaciones en un pueblo llamado Rosetta, en el delta del Nilo, en Egipto, una piedra con textos en tres lenguajes desconocidos. La utilidad de descifrar estos textos era obvia, pues abr�a las puertas a la posibilidad de interpretar los jerogl�ficos egipcios. La piedra cay� despu�s en manos de los ingleses, quienes la llevaron al Museo Brit�nico, donde a�n se encuentra. Muchos intentaron descifrar la piedra sin �xito alguno, hasta que en 1814 Young se interes� en ella y logr� descifrarla. En 1821, dos a�os despu�s de que Young public� sus resultados, Jean Fran�ois Champollion, un egipt�logo profesional, hizo una mejor y m�s completa interpretaci�n, pero sin reconocer los esfuerzos de Young.

En 1808, Etienne-Louis Malus (1775-1812) descubri� la polarizaci�n de la luz por medio de la reflexi�n al observar que la luz, al reflejarse en vidrio o agua, presentaba el mismo fen�meno que cada una de las dos im�genes que aparec�an por birrefringencia al pasar a trav�s del espato de Islandia. Este fen�meno consiste en que, al ser observadas las im�genes a trav�s de un segundo trozo de espato de Islandia, la imagen aparece o desaparece seg�n su orientaci�n. A este fen�meno se le llam� polarizaci�n.

Poco despu�s, en 1815, sir David Brewster (1781-1868) hizo un estudio bastante completo del fen�meno de la polarizaci�n. Es interesante saber un poco sobre la vida de Brewster, quien naci� en 1781 en Jedburgh, Roxburghire, Escocia. Comenz� sus actividades en �ptica a la temprana edad de diez a�os, construyendo un telescopio. A los doce a�os ingres� a la Universidad de Edimburgo. En 1812 Brewster se enter� del descubrimiento de Malus sobre la polarizaci�n. Al hacer experimentos sobre este fen�meno, pronto encontr� que la luz reflejada queda polarizada completamente cuando la tangente del �ngulo de incidencia es igual al �ndice de refracci�n. A este �ngulo se le conoce ahora como �ngulo de Brewster. Una an�cdota interesante de este investigador es que invent� el famos�simo caleidoscopio, que tuvo un �xito y popularidad grand�simos. Trat� sin �xito de patentarlo, y ese fracaso lo defraud� profundamente.

El establecimiento definitivo de una teor�a ondulatoria transversal de la luz m�s formal se obtuvo alrededor de 1823 en Normand�a, gracias a los trabajos tanto te�ricos como experimentales de Augustin Fresnel, quien naci� en Broglie, Francia, el 10 de mayo de 1788 y muri� en el a�o de 1827. Con su teor�a se explicaban todos los fen�menos luminosos hasta entonces conocidos.

Es curioso que, a pesar de que cada d�a se entend�a mejor la naturaleza de la luz, no se hab�a todav�a medido, a finales del siglo XVII, su velocidad de propagaci�n. La primera medici�n fue efectuada en forma indirecta mediante medios astron�micos por Ole Romer (1644-1710) en 1673. Su m�todo consisti� en medir los periodos de traslaci�n de los sat�lites de J�piter alrededor del planeta. No fue sino hasta 1849 cuando H. L. Fizeau (1819-1896) midi� por primera vez en forma directa la velocidad de propagaci�n de la luz. Le�n Foucault prob� experimentalmente en 1850 que la velocidad de la luz es menor en un medio denso que en el vac�o, obteniendo que el factor en el que se reduce esta velocidad al entrar a un cuerpo transparente es justamente el valor del �ndice de refracci�n. As�, se puede escribir:

c/ v = n

donde v es la velocidad de la luz en el medio y c es la velocidad de la luz en el vac�o.

En 1864 ya estaba aceptada la teor�a ondulatoria; sin embargo, era completamente desconocido el tipo de onda que era la luz. En este a�o el f�sico escoc�s James Clerk Maxwell (1831-1879) plante� su teor�a electromagn�tica de la luz, con la que prob� que la luz es una onda electromagn�tica transversal de la misma naturaleza que las ondas de radio, que a�n no se hab�an descubierto, diferenci�ndose de �stas s�lo en que su frecuencia es mucho mayor, como se muestra en la figura 14. Maxwell tuvo tanto �xito con su teor�a que pudo explicar cualitativa y cuantitativamente todos los fen�menos luminosos conocidos entonces y aun predecir otros m�s. Lo m�s interesante fue que obtuvo el valor de la velocidad en el vac�o calcul�ndola te�ricamente a partir de constantes el�ctricas conocidas del vac�o.

En 1883, Gustav Kirchhoff (1824-1887) deriv� en Berl�n su teor�a escalar de la difracci�n. Esta teor�a se puede considerar como una aproximaci�n a la de Maxwell o como una mejor�a de la de Fresnel. Heinrich Rudolph Hertz (1857-1894) en 1886 en Alemania demostr� experimentalmente la existencia de las ondas de radio, confirmando as� sin lugar a dudas la teor�a electromagn�tica de Maxwell.

Al calentarse un cuerpo cualquiera emite luz, generalmente no monocrom�tica, con una distribuci�n de longitudes de onda (colores) a la que llamamos "espectro", que depende tanto de la temperatura como del tipo de material del que est� hecho el cuerpo.

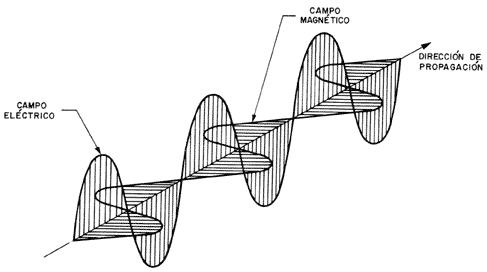
Figura 14. Una onda luminosa, con el campo el�ctrico vertical y el campo magn�tico horizontal.

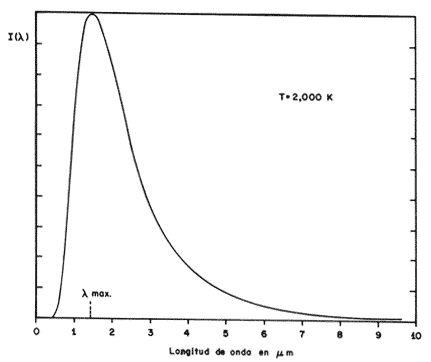
Figura 15. Espectro de emisi�n del cuerpo negro.

Si un cuerpo, bien sea por su color o por su forma, absorbe toda la energ�a luminosa que le llega, se llama en f�sica "cuerpo negro". Este cuerpo negro puede hacerse con una esfera hueca y cerrada, con un agujerito muy peque�o para observar la radiaci�n luminosa proveniente del interior cuando se le calienta. Ahora bien, el espectro de la radiaci�n luminosa emitida por un cuerpo negro, depende solamente de su temperatura y no del material del que est� hecho el cuerpo. Esta distribuci�n o espectro tiene la forma representada en la figura 15. Hasta el a�o 1895 el espectro observado era muy dif�cil de explicar por medio de una teor�a f�sica adecuada. La teor�a buscada tuvo que romper algunos de los principales conceptos de la f�sica de entonces, lo que qued� a cargo de Max Carl Ernst Ludwig Planck, nacido en Kiel, Alemania, el 23 de abril de 1858. En diciembre 14 de 1900, Planck envi� un reporte a la Physical Society de Berl�n, en el que daba una explicaci�n exacta de la forma del espectro de la radiaci�n del cuerpo negro. Esta teor�a inclu�a un concepto revolucionario: el "cuanto" de energ�a luminosa, llamado tambi�n m�s tarde "fot�n". Seg�n este concepto, la cantidad m�s peque�a en la que podemos fragmentar o dividir la energ�a luminosa tiene un valor que depende de la frecuencia V, seg�n la relaci�n E = h v donde la h denota una constante universal, la llamada de Planck.

Planck introdujo el concepto de cuanto de energ�a como una mera necesidad matem�tica, para poder obtener el resultado correcto en su teor�a, pero no pudo darle la interpretaci�n f�sica correcta. Planck recibi� el premio Nobel de f�sica en 1918. Vivi� hasta los 89 a�os, conservando siempre una gran actividad intelectual.

H. R. Hertz, descubridor de las ondas de radio, encontr� tambi�n el efecto fotoel�ctrico, que consiste en la expulsi�n de electrones de un metal cuando incide un haz luminoso sobre �l (Figura 16). La energ�a cin�tica de los electrones expulsados era tanto mayor cuanto mayor era la frecuencia de la luz que iluminaba el metal. Ninguna teor�a f�sica de la �poca pod�a explicar este fen�meno. La explicaci�n satisfactoria tanto cualitativa como cuantitativa de este efecto la dio Albert Einstein, quien postul� que la luz est� formada por unas part�culas a las que G. N. Lewis llam� fotones en 1923. Los fotones tienen una energ�a que depende de la frecuencia, de la misma manera que los cuantos de Planck. Esta teor�a completaba muy bien la teor�a de la radiaci�n del cuerpo negro de Planck. Con esto quedaba bien cimentado por primera vez el concepto de fot�n. Esta teor�a, y no la de la relatividad, fue la que le dio el premio Nobel de f�sica a Einstein en 1905.

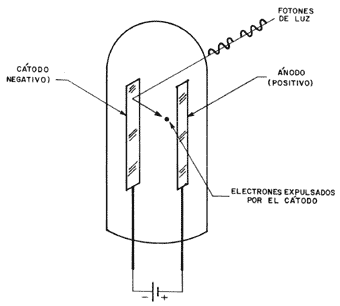
Figura 16. Efecto fotoel�ctrico.

Se presentaba entonces una dualidad de la luz muy dif�cil de concebir, pues no pod�a ser una onda, y al mismo tiempo una part�cula. El franc�s Louis Victor de Broglie (1892-1987) trata de resolver el enigma afirmando que onda y corp�sculo son solamente dos manifestaciones diferentes del mismo ente, que se presentan seg�n las circunstancias del experimento. Con ello predice entonces que lo que suponemos que son solamente part�culas, como los electrones, bajo ciertas circunstancias deben manifestarse como ondas. Debido a esta predicci�n que se confirm� m�s tarde, recibi� el premio Nobel de f�sica en 1919. De Broglie afirm� que la longitud de onda de la onda asociada a una part�cula est� dada por:

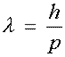
donde p es el momento lineal de la part�cula. Tratando de demostrar lo anterior, Davidson y Germer hacen pasar un haz de electrones a trav�s de la red de un cristal. Se observ� que los electrones producen, al chocar sobre una pantalla despu�s de atravesar el cristal, un patr�n similar al producido por una onda que atraviesa una rejilla de difracci�n.

Ahora sabemos que todas las ondas electromagn�ticas son de la misma naturaleza y que s�lo difieren entre s� por su longitud de onda. El cuadro 1 muestra el espectro electromagn�tico completo, con sus longitudes de onda aproximadas. La dualidad onda-fot�n persiste hasta la fecha, as� que podemos hablar de la radiaci�n electromagn�tica tanto en t�rminos de una onda como de un flujo de fotones. El fot�n contiene la cantidad m�s peque�a de energ�a E que podemos aislar de esta radiaci�n, de frecuencia v relacionadas por E = h v. Mientras m�s grande sea la longitud de onda, m�s peque�a es la frecuencia y por lo tanto m�s peque�a la energ�a E del fot�n. Debido a ello, mientras m�s grande sea la longitud de onda, m�s dif�cil ser� detectar el fot�n individualmente. Como consecuencia, las ondas de radio y televisi�n tambi�n est�n formadas por fotones, pero son de energ�a tan peque�a que jam�s se han podido detectar individualmente.

III.2. LAS ONDAS LUMINOSAS

Como conclusi�n de toda la historia anterior se desprende que, en ciertos experimentos, se puede considerar a la luz como una onda transversal, mientras que en otros es necesario considerarla como un flujo de part�culas llamadas fotones, cuya energ�a individual depende de la frecuencia de la onda. Sin embargo, en la gran mayor�a de los casos, sobre todo en aquellos en los que interviene la metrolog�a, es suficiente utilizar el concepto de onda transversal.

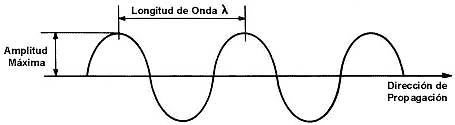
Figura 17. Par�metros importantes en una onda.

Conviene recordar varios conceptos y definiciones relacionados con las ondas. Uno de ellos es la longitud de onda l , que es la distancia entre dos crestas o dos valles consecutivos, como se muestra en la figura 17. La frecuencia V, es el n�mero de oscilaciones en un segundo, es decir, el n�mero de crestas que pasan por un lugar en un segundo. Estas dos cantidades no son independientes, sino que est�n relacionadas entre s� por la velocidad v, con la que se propaga la luz. Si el medio en el que viaja la luz es el vac�o, esta velocidad se representa por c, y tiene un valor de 299 792 kil�metros por segundo. La distancia de la Tierra a la Luna es aproximadamente de 384 500 kil�metros, por lo que la luz atraviesa esa distancia en poco m�s de un segundo. Otra manera de imaginar la magnitud de la velocidad de la luz es pensar que esta distancia corresponde aproximadamente a ocho vueltas alrededor de la Tierra. La f�rmula que relaciona estos tres conceptos b�sicos de una onda es:

l v= c

Podemos darnos cuenta f�cilmente de que mientras m�s grande sea la longitud de onda, menor es la frecuencia, y viceversa. La longitud de onda tiene diferentes valores seg�n el color de la luz, como se ve en el cuadro 1, pero va desde aproximadamente 350 nm para el violeta hasta 650 nm para el rojo. Recordando ahora que un nm (nan�metro) es 10^-9 metros, podemos ver que estas longitudes de onda son de 3.5 y 6.5 diezmil�simos de mil�metro, las cuales son obviamente longitudes muy peque�as.

III.3. LA INTERFEROMETR�A Y SU HISTORIA

La interferometr�a se basa en el fen�meno de la interferencia, que podemos producir cuando dos ondas luminosas de exactamente la misma frecuencia se superponen sobre una pantalla. Adem�s de tener la misma frecuencia, estas ondas deben ser sincr�nicas, es decir que sus diferencias de fase, y por lo tanto las distancias entre las crestas de ambas ondas, deben permanecer constantes con el tiempo. Esto es pr�cticamente posible s�lo si la luz de ambas ondas que se interfieren proviene de la misma fuente luminosa. Pero si es solamente una fuente luminosa la que produce la luz, los dos haces luminosos que se interfieren deben generarse de alguna manera del mismo haz. Existen dos procedimientos para lograr esto: denominamos al primero divisi�n de amplitud y al segundo divisi�n de frente de onda. Usando estos dos m�todos b�sicos se han dise�ado una gran cantidad de interfer�metros, con los que se pueden efectuar medidas sumamente precisas. La figura 18 muestra dos interfer�metros muy comunes, el primero es el sistema de dos rendijas de Young, que produce interferencia por frente de onda y el segundo es el de Michelson, que produce interferencia por divisi�n de amplitud.

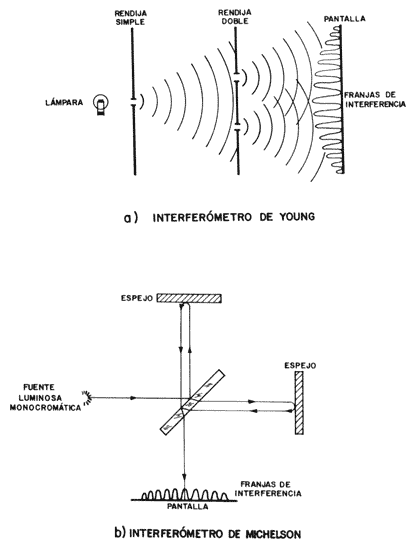
Figura 18. (a) Interfer�metro de Young, que funciona por divisi�n de frente de onda y (b) interfer�metro de Michelson, que funciona por divisi�n de amplitud.

Sin duda el personaje m�s importante en el terreno de la interferometr�a es Albert Abraham Michelson (1852-1931), que naci� un 19 de diciembre en Strzelno, Polonia. A los tres a�os de edad emigr� con sus padres, primero a Europa occidental y despu�s a Nueva York, posiblemente para huir del antisemitismo. Despu�s de viajar por todo el continente americano, se establecieron finalmente en San Francisco. Cuando ten�a 16 a�os, su padre se enter� de que exist�a la posibilidad de que su hijo ingresara a la Academia Naval de los Estados Unidos. Los problemas para lograr el ingreso fueron tan grandes que tuvieron que solicitar la ayuda personal del presidente Grant. Finalmente Michelson logr� ingresar, y se gradu� en 1873. En el curso de su carrera demostr� una gran vocaci�n para la �ptica, m�s que para las actividades navales.

Despu�s de graduarse, Michelson empez� a trabajar en el Departamento Naval de Annapolis, donde su primer trabajo fue medir la velocidad de la luz con el mismo m�todo que Le�n Foucault hab�a empleado a�os antes. Su resultado super� notablemente al de Foucault. Despu�s de esto le fue otorgado permiso para estudiar un a�o en Europa. A su regreso ingres� a la reci�n fundada Case School of Applied Science en la ciudad de Cleveland, donde conoci� al profesor de qu�mica Edwin Williams Morley (1838-1923). Juntos se propusieron llevar a cabo un experimento interferom�trico que hab�a comenzado Michelson durante su estancia en Europa, para determinar si la Tierra estaba en reposo o en movimiento con respecto al �ter, es decir, al medio en el que se propagaba la luz. Despu�s de repetir el experimento varias veces y de atravesar m�ltiples calamidades y accidentes, en 1888 llegaron a la conclusi�n de que la franja de interferencia no se mov�a de posici�n cuando ellos lo esperaban, y por lo tanto se requer�a una explicaci�n que no pod�an encontrar, para resolver satisfactoriamente el resultado del experimento.

Uno de los intentos de explicaci�n era suponer que el �ter estaba en reposo en relaci�n con la Tierra. Sin embargo, esta conclusi�n no era aceptable, porque otros experimentos de varios investigadores demostraban que esto era imposible. Fueron muy numerosos los intentos de explicar el resultado inesperado del experimento, pero todos fracasaron porque ninguno pod�a dar una explicaci�n satisfactoria para todas las observaciones relacionadas con la teor�a.

Mientras tanto, con motivaciones muy diferentes e independientes, Albert Einstein (1879-1955), nacido en Ulm, Alemania, elabor� su teor�a de la relatividad especial, que postulaba que la velocidad de la luz era siempre exactamente la misma en el vac�o, independientemente de las velocidades relativas de la fuente luminosa y del observador. Esta teor�a hac�a completamente innecesaria la hip�tesis de la existencia del �ter. De esta manera quedaba explicado el resultado del experimento de Michelson y Morley. No se hablar� especialmente en este libro sobre la vida y personalidad de Einstein, por ser sumamente conocidas. Baste con decir que Einstein y Newton son los dos cient�ficos m�s grandes que ha tenido la humanidad.

Albert Michelson hizo una gran multitud de experimentos meterol�gicos, que sin lugar a dudas lo hacen merecedor del nombre de padre de la interferometr�a. Otro de sus trabajos importantes fue la medici�n de longitudes por medio de interfer�metros, superando la precisi�n de cualquier medida efectuada hasta entonces. Michelson recibi� el premio Nobel de f�sica por sus trabajos interferom�tricos de precisi�n, en 1901.

III.4. APLICACIONES DE LA INTERFEROMETR�A

La interferometr�a es ahora una herramienta indispensable en muchas actividades en las que sea necesario realizar mediciones. A partir de 1947 se han extendido estas t�cnicas a las ondas de radio, inici�ndose as� la radiointerferometr�a astron�mica. Hoy en d�a, por medio de t�cnicas interferom�tricas se pueden realizar una gran variedad de medidas sumamente precisas, entre las que podemos mencionar las siguientes:

a) Medida y definici�n del metro patr�n. El primero que tom� la longitud de onda de la luz como referencia para especificar longitudes de objetos fue Michelson. Esto se hace por medio del interfer�metro que se muestra en la figura 19, donde el primer objetivo es medir la separaci�n entre dos espejos, los que forman un sistema llamado etal�n. La separaci�n entre los espejos del etal�n es un m�ltiplo entero de medias longitudes de onda de la luz empleada, a fin de que los haces reflejados en ambos espejos del etal�n est�n en fase. El proceso es bastante laborioso, pues hay necesidad de usar un gran n�mero de etalones, donde cada uno tiene aproximadamente el doble de longitud que el anterior. La raz�n de este largo proceso es que no es posible contar las franjas de interferencia que aparecen al ir moviendo uno de los espejos hasta llegar a la distancia de un metro. La limitaci�n es la coherencia del haz luminoso, que se describir� m�s tarde en la secci�n de l�seres. Actualmente, con el l�ser, es mucho m�s simple la medici�n del metro patr�n por interferometr�a.

En 1960 el metro fue definido como igual a 1650 763.73 longitudes de onda en el vac�o, de la luz emitida en una cierta l�nea espectral del kript�n-86. Sin embargo, en lugar de definir el metro y luego medir la velocidad c de la luz usando esta definici�n, es posible hacer lo contrario.

Es decir, se define primero la velocidad c de la luz como una cierta cantidad de metros recorridos en un segundo, de donde podemos escribir:

c = d/t

El siguiente paso es definir el metro como la distancia recorrida por la luz en un tiempo igual a 1 /c. Esto es lo que actualmente se ha hecho para definir el metro.

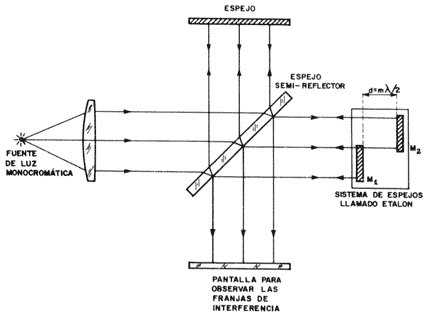
Figura 19. Interfer�metro de Michelson con etal�n, para medir longitudes

b) Medida de las deformaciones de una superficie. Frecuentemente, debido a causas muy variadas, una superficie puede tener deformaciones peque��simas que no son detectables a simple vista. A pesar de su reducida magnitud, estas deformaciones pueden ser el s�ntoma de problemas graves presentes o futuros. Como ejemplo, podemos mencionar una fractura de un elemento mec�nico de un avi�n o de una m�quina. Otro ejemplo es un calentamiento local anormal en un circuito impreso o en una pieza mec�nica sujeta a fricci�n. Finalmente, Otro ejemplo es una deformaci�n producida por esfuerzos mec�nicos que ponen en peligro la estabilidad del cuerpo que los sufre. Es aqu� donde la interferometr�a tiene un papel muy importante, detectando y midiendo estas peque��simas deformaciones de la superficie. Esta aplicaci�n de las t�cnicas interferom�tricas es especialmente �til y poderosa si se le combina con t�cnicas hologr�ficas, como se ver� m�s adelante, en un proceso llamado interferometr�a hologr�fica. La figura 20 muestra un ejemplo de deformaci�n local de la superficie de una cubeta de pl�stico, medida con interferometr�a hologr�fica.

Figura 20. Detecci�n interferom�trica de deformaciones.

Figura 21. Interferograma del espejo de un telescopio.

c) Determinaci�n de la forma exacta de una superficie. Las superficies �pticas de los instrumentos modernos de alta precisi�n tienen que tallarse de tal manera que no tengan desviaciones de la forma ideal, mayores de una fracci�n de la longitud de onda de la luz. Para hacer el problema todav�a m�s dif�cil, la superficie muy frecuentemente no es esf�rica sino de cualquier otra forma, a la que de modo general se le denomina asf�rica. Esta superficie asf�rica puede ser, por ejemplo, un paraboloide o un hiperboloide de revoluci�n, como ocurre en los telescopios astron�micos, donde adem�s la superficie a tallar puede ser de varios metros de di�metro. Es f�cil comprender lo dif�cil que resulta tallar una superficie tan grande. Sin embargo, el problema principal es medir las deformaciones de la superficie respecto a su forma ideal. Esto se hace mediante la interferometr�a, con t�cnicas muy diversas y complicadas que no es posible describir aqu�. La figura 21 muestra el interferograma del espejo principal o primario de un telescopio. Si la superficie fuera perfectamente esf�rica, las franjas de interferencia ser�an rectas. La peque�a curvatura de las franjas se debe a que la superficie es ligeramente elipsoidal en lugar de esf�rica, aunque la desviaci�n es apenas alrededor de media longitud de onda, lo que es aproximadamente tres diezmil�simas de mil�metro.

d) Alineaci�n de objetos sobre una l�nea recta perfecta. Es frecuente que aparezca la necesidad de tener una l�nea recta de referencia muy precisa en una gran cantidad de actividades ingenieriles de tipo muy diverso. Por ejemplo, la bancada o base de un torno de alta precisi�n debe ser tanto m�s recta cuanto m�s fino sea el torno. En este problema y muchos otros en los que se requiera alinear algo con muy alta precisi�n, la interferometr�a es un auxiliar muy �til.

e) Determinaci�n muy precisa de cambios del �ndice de refracci�n en materiales transparentes. Los vidrios �pticos, pl�sticos o cristales que se usan en las lentes, prismas y dem�s elementos �pticos tienen que ser de una alta homogeneidad tanto en su transparencia como en su �ndice de refracci�n. Esto es especialmente necesario si el instrumento �ptico que los usa es de alta precisi�n. Esta homogeneidad de los materiales transparentes se mide con la tolerancia que sea necesaria por medio de interferometr�a.

f) Determinaci�n muy precisa de velocidades o de variaciones en su magnitud. Cuando una fuente luminosa se mueve respecto al observador, es bien sabido que la longitud de onda de la luz tiene un cambio aparente, alarg�ndose o acort�ndose, seg�n que el objeto luminoso se aleje del observador o se acerque a �l, respectivamente. Este es el llamado efecto Doppler, que se descubri� primero para las ondas sonoras y posteriormente para la luz. Por medio de interferometr�a se pueden detectar y medir variaciones sumamente peque�as en la longitud de onda, lo que permite detectar movimientos o cambios tambi�n muy peque�os en la velocidad de un objeto. Esta propiedad se ha usado en muy diversas aplicaciones, entre otras, la medida de la velocidad del flujo de l�quidos o de gases.

g) Medici�n de �ngulos. Los �ngulos, al igual que las distancias, tambi�n se pueden medir con muy alta precisi�n por medio de t�cnicas interferom�tricas. Por ejemplo, el paralelismo entre las dos caras de una placa de vidrio de caras planas y paralelas, o el �ngulo recto entre las dos caras de un prisma se pueden medir con una incertidumbre mucho menor de un segundo de arco, lo que es totalmente imposible de lograr por otros m�todos.

La lista podr�a continuarse, pero con estos ejemplos es suficiente para darnos cuenta de la enorme utilidad de la interferometr�a, o sea del uso de las ondas de luz como unidad de medida.