VI. PROCESAMIENTO DE IM�GENES
EL PROCESAMIENTO de im�genes tiene como objetivo mejorar el aspecto de las im�genes y hacer m�s evidentes en ellas ciertos detalles que se desean hacer notar. La imagen puede haber sido generada de muchas maneras, por ejemplo, fotogr�ficamente, o electr�nicamente, por medio de monitores de televisi�n. El procesamiento de las im�genes se puede en general hacer por medio de m�todos �pticos, o bien por medio de m�todos digitales, en una computadora. En la siguiente secci�n describiremos muy brevemente estos dos m�todos, pero antes se har� una s�ntesis brev�sima de los principios matem�ticos impl�citos en ambos m�todos, donde el teorema de Fourier es el eje central.
El matem�tico Jean-Baptiste-Joseph Fourier (1768-1830) naci� en Auxerre, alrededor de 160 km al sureste de Par�s. Perdi� a sus padres a la temprana edad de ocho a�os, quedando al cuidado del obispo de Auxerre, gracias a la recomendaci�n de una vecina. Desde muy peque�o mostr� una inteligencia y vivacidad poco comunes. Sigui� una carrera religiosa en una abad�a, al mismo tiempo que estudiaba matem�ticas, para m�s tarde dedicarse a impartir clases. Sus clases eran muy amenas, pues constantemente mostraba una gran erudici�n y conocimientos sobre los temas m�s variados.
Fourier estaba muy interesado en la teor�a del calor, y adem�s ten�a una gran obsesi�n pr�ctica por �l. Se dice que manten�a su habitaci�n tan caliente que era muy inc�moda para quienes lo visitaban, y que aparte de eso, siempre llevaba puesto un grueso abrigo. Algunos historiadores atribuyen esta excentricidad a los tres a�os que pas� en Egipto con el ej�rcito de Napole�n Bonaparte.
La teor�a de Fourier se consider� tan importante desde de sus inicios, que lord Kelvin dijo de ella: "El teorema de Fourier no solamente es uno de los resultados m�s hermosos del an�lisis moderno, sino que adem�s se puede decir que proporciona una herramienta indispensable en el tratamiento de casi todos los enigmas de la f�sica moderna."
El teorema de Fourier afirma que una gr�fica o funci�n, cualquiera que sea su forma, se puede representar con alta precisi�n dentro de un intervalo dado, mediante la suma de una gran cantidad de funciones senoidales, con diferentes frecuencias. Dicho de otro modo, cualquier funci�n, sea o no sea peri�dica, se puede representar por una superposici�n de funciones peri�dicas con diferentes frecuencias. El teorema nos dice de qu� manera se puede hacer esta representaci�n, pero hablar de �l va m�s all� del objeto de este libro.
La variaci�n de la irradiancia o brillantez de una imagen, medida a lo largo de una direcci�n cualquiera es entonces una funci�n que se puede representar mediante el teorema de Fourier, con una suma de distribuciones senoidales de varias frecuencias. Sin entrar en detalles t�cnicos innecesarios, simplemente afirmaremos aqu� que atenuar o reforzar individualmente algunas de estas componentes senoidales puede tener un efecto dram�tico en la calidad de una imagen, mejor�ndola o empeor�ndola, seg�n el caso. Este es el fundamento del procesamiento de im�genes, tanto por medios �pticos como digitales, que ahora describiremos.
Los principios del procesamiento �ptico de im�genes est�n bien establecidos desde el siglo pasado, cuando se desarroll� la teor�a de la difracci�n de la luz. Sin embargo, su aplicaci�n pr�ctica data apenas del principio de la d�cada de los sesenta, cuando se comenz� a disponer del rayo l�ser.
El procesamiento �ptico se basa en el hecho de que la imagen de difracci�n de Fraunhofer de una transparencia colocada en el plano focal frontal de una lente es una distribuci�n luminosa que representa la distribuci�n de las frecuencias de Fourier que componen la imagen, a la que se le llama t�cnicamente transformada de Fourier.
Consideremos el arreglo �ptico de la figura 42. En el plano focal frontal de la lente L1 se ha colocado la transparencia T, la cual est� siendo iluminada por un haz de rayos paralelos provenientes de un l�ser de gas. Sobre el plano focal F1 de la lente L1 se forma una distribuci�n luminosa que representa la transformada de Fourier de la transparencia. Si ahora se coloca otra lente L2 como se muestra en la misma figura, se puede formar una imagen de la transparencia en el plano focal F2 de esta lente. Si ahora se coloca cualquier objeto o diafragma sobre el plano F1, se pueden eliminar las porciones que se deseen de la transformada de Fourier de la transparencia, eliminando as� de la imagen las frecuencias de Fourier deseadas.
Cada porci�n de la transformada de Fourier corresponde a una frecuencia espacial diferente sobre el objeto. Por lo tanto, mediante los diafragmas adecuados se pueden eliminar las frecuencias espaciales, llamadas tambi�n de Fourier, que se deseen quitar.
Figura 42. Procesamiento �ptico de im�genes. (a) imagen original, con l�neas
de barrido, tipo imagen de televisi�n; (b) transformada de Fourier del objeto;
(c) transformada de Fourier modificada, despu�s de filtrar y (d) imagen procesada,
sin las l�neas de barrido.
Al igual que en el caso del procesamiento �ptico, los principios fundamentales del procesamiento digital de im�genes est�n establecidos hace muchos a�os, pero no se llevaban a cabo debido a la falta de computadoras. Con la aparici�n de las computadoras de alta capacidad y memoria, era natural que se comenzara a desarrollar este campo. Uno de los primeros lugares donde se empez� a realizar el procesamiento digital fue en el Jet Propulsion Laboratory, en 1959, con el prop�sito de mejorar las im�genes enviadas por los cohetes. Los resultados obtenidos en un tiempo relativamente corto fueron tan impresionantes que muy pronto se extendieron las aplicaciones del m�todo a otros campos.
Figura 43. Divisi�n de una imagen en pixeles.
El procesamiento digital de im�genes se efect�a dividiendo la imagen en un arreglo rectangular de elementos, como se muestra en la figura 43. Cada elemento de la imagen as� dividida se conoce con el nombre de pixel. El siguiente paso es asignar un valor num�rico a la luminosidad promedio de cada pixel. As�, los valores de la luminosidad de cada pixel, con sus coordenadas que indican su posici�n, definen completamente la imagen.
Todos estos n�meros se almacenan en la memoria de una computadora.
El tercer paso es alterar los valores de la luminosidad de los pixeles mediante las operaciones o transformaciones matem�ticas necesarias, a fin de hacer que resalten los detalles de la imagen que sean convenientes. El paso final es pasar la representaci�n de estos pixeles a un monitor de televisi�n de alta definici�n, con el fin de mostrar la imagen procesada (Figura 44).
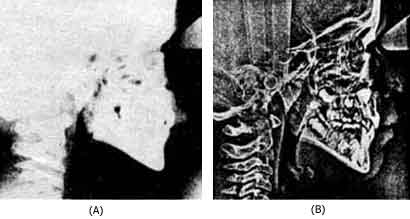
Figura 44. Procesamiento digital de im�genes. Cefalograma en el que se han
reforzado las componentes de Fourier de alta frecuencia. (Tomado de S. W. Oka
y H. J. Trussell, The Angle Ortodontist, 48, n�m. 1, 80, 1978). (a) Imagen
original y (b) imagen procesada.
VI.3. UTILIDAD DEL PROCESAMIENTO DE IM�GENES
La utilidad del procesamiento de im�genes es muy amplia y abarca muchos campos. Un ejemplo son las im�genes obtenidas con fines de diagn�stico m�dico. Otro ejemplo son las im�genes a�reas obtenidas para realizar ex�menes del terreno. Mediante este m�todo se pueden analizar los recursos naturales, las fallas geol�gicas del terreno, etc�tera.
