II. HISTORIA DE LA COMPUTACI�N
EN LA historia de la ciencia, hay ciertos momentos claves en los que el ingenio e inteligencia de ciertas personas, aunados a toda una situaci�n social e ideol�gica propicias, les permiten percibir algo que nadie antes hab�a sido capaz de ver. En muchas ocasiones esta revoluci�n en los conceptos viene acompa�ada de innovaciones tecnol�gicas que constituyen grandes saltos en el desarrollo de nuevos aparatos. De esta manera, nos encontramos con que en general el avance cient�fico-tecnol�gico tiene dos tipos de etapas: en la primera surge una idea o descubrimiento innovador muy importante, y la segunda comprende los tiempos durante los cuales se maduran y establecen las ideas. Durante estos periodos, se construyen aparatos cada vez m�s elaborados con base en estos principios. Este proceso contin�a hasta que surge una nueva idea que permite de nueva cuenta un avance significativo.
Con esta idea en mente, podr�amos dividir la historia de la computaci�n en varias etapas, cada una caracterizada por una revoluci�n tecnol�gica importante. A continuaci�n relataremos de manera muy general el desarrollo de la computaci�n, desde sus or�genes hasta finales de los a�os ochenta.
Puede decirse que la historia de la computaci�n comienza cuando el hombre adquiere la necesidad de contar. Seguramente en un principio el hombre comenz� a contar con los dedos, para despu�s hacerlo mediante marcas en el piso o utilizando piedras. Con la invenci�n de la escritura, diferentes civilizaciones encontraron sendas maneras de contar y m�s tarde, de efectuar operaciones. La figura 6 nos muestra, de una manera comparativa, algunos sistemas numerales.
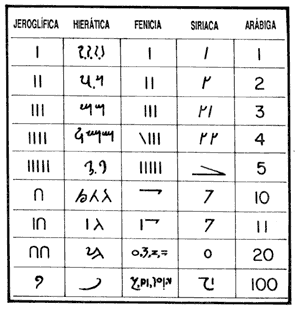
Figura 6. Esta figura nos muestra algunos sistemas numerales.
Figura 7. En la numeraci�n maya un punto representa una unidad, una barra corresponde a cinco unidades, y el n�mero cero es representado por una concha. Combinando estos signos pueden escribirse los n�meros del 0 al 19. Para designar N�meros mayores al 19 se utiliza el sistema de posiciones: de abajo hacia arriba, la n-�sima posici�n representa unidades de n-�simo orden.
Una de las escrituras m�s antiguas que se conoce es la egipcia. Esta civilizaci�n adopt� un sistema de contar de diez en diez, de manera que marcaban las unidades con l�neas verticales y las decenas con un signo similar a la U invertida. Otras culturas adoptaron sistemas m�s complicados; por ejemplo, los babilonios contaban de 60 en 60, y aunque su sistema era muy poco pr�ctico, se cree que de ellos provienen las bases del sistema actual de contar los minutos y los segundos.
Otra numeraci�n antiguamente utilizada fue la romana, la cual era muy simple y permit�a efectuar operaciones aritm�ticas aunque no con mucha sencillez. A�n perdura la tradici�n de utilizarla en algunos contextos espec�ficos; por ejemplo, en las car�tulas de los relojes, para denominar los tomos o cap�tulos de los libros, para escribir algunas fechas, etc�tera.
Entre las culturas de Am�rica, es interesante se�alar que los mayas contaron con un sistema numeral vigesimal muy avanzado y utilizaron el cero aun antes que en Europa o Asia. La figura 7 nos muestra esta numeraci�n.
Figura 8. En el sistema decimal se utiliza un criterio de posiciones con el cual cada d�gito tiene un peso diferente, de acuerdo con una base diez. Esta figura nos muestra la forma en que se construye el n�mero 1 968.
Podr�amos continuar esta lista se�alando m�s culturas y explicando sus sistemas de numeraci�n, sin embargo, tan s�lo queremos hacer hincapi� en lo siguiente: la forma en que contamos actualmente, eso es, utilizando el sistema decimal (ar�bico), no es ni la �nica posible ni la �nica correcta, sino s�lo una forma que hemos heredado de nuestros antepasados y que ha sobrevivido por ser simple y adecuada para nosotros debido a que tenemos diez dedos en las manos. Los principios de esta numeraci�n se ilustran en la figura 8.
El siguiente paso en el desarrollo de la computaci�n se dio con la invenci�n de aparatos �tiles para efectuar operaciones matem�ticas. El �baco es la primera calculadora o computadora de que tenemos noticias. Aunque se invent� hace aproximadamente 4 000 a�os, a�n tiene un uso muy amplio en algunos pa�ses de Asia, debido a que se trata de una calculadora muy r�pida y pr�ctica, �til para efectuar operaciones de adici�n, substracci�n, multiplicaci�n y divisi�n. Este artefacto se muestra en la figura 9.
Muchos a�os tuvieron que pasar antes de que se lograran progresos en el desarrollo de nuevas calculadoras. En 1617, el escoc�s John Napier inventa los llamados huesos de Napier o tablas de multiplicar (de donde proviene el nombre utilizado hasta nuestros d�as). �stos consisten de una regla fija y otra m�vil que se desliza sobre la primera, de manera que deja ver el producto de dos n�meros cualesquiera (v�ase la figura 10). Posteriormente las tablas de Napier evolucionaron hasta llegar a la regla de c�lculo, la cual funciona con el mismo principio pero es �til para llevar a cabo operaciones de multiplicaci�n, divisi�n y ra�z cuadrada, entre otras. Debido a su portabilidad, este artefacto tuvo una gran acogida en el mundo occidental y fue de uso frecuente hasta hace pocos a�os, cuando se generaliz� el uso de las calculadoras de bolsillo.
A mediados del siglo XVII se inicia una nueva era de calculadoras mec�nicas cuando, en 1642, Blaise Pascal, quien s�lo contaba con 19 a�os de edad, introduce una m�quina sumadora mec�nica con el objeto de facilitar los c�lculos de su padre (Figura 11). Esta m�quina consist�a en un sistema con ruedas peque�as acopladas entre s� y que, de derecha a izquierda correspond�an a unidades, decenas, centenas, etc�tera. Estas ruedas se encontraban divididas en 10 partes iguales; de manera que para efectuar una suma se hac�an girar manualmente un n�mero de pasos acorde con el n�mero que se deseaba introducir. La rotaci�n completa de un c�rculo en la direcci�n positiva, causaba autom�ticamente que el c�rculo a su izquierda avanzara una posici�n. Para efectuar sustracciones el proceso era el inverso.
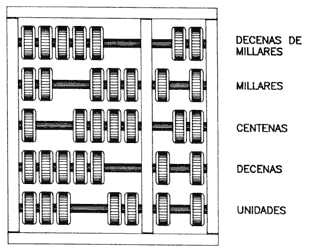
Figura 9. En el �baco, cada barra horizontal contiene siete m�viles separadas por una barra vertical. Aqu�llas en el lado izquierdo valen uno, y las del lado derecho valen cinco; el n�mero cero est� representado cuando todas las cuentas est�n alejadas de la barra central. Las sumas se efect�an al mover, hacia la barra central, las cuentas correspondientes a la cantidad que se desea sumar.
Algunos a�os m�s tarde, Leibniz inventa una m�quina similar a la de Pascal pero m�s compleja, la cual pod�a sumar, restar, multiplicar y dividir. Es la computadora, ilustrada en la figura 12, se emple� extensivamente hasta el advenimiento de las computadoras electr�nicas.
LA ERA DE LA PROGRAMACI�N SE INICIA
Los siguientes avances significativos se logran hasta el siglo XIX, cuando Joseph Jacquard, quien era obrero en una f�brica de sedas de Lyon, introduce la idea de programar m�quinas mediante el uso de tarjetas perforadas. La invenci�n de Jacquard consisti� en un telar que utilizaba tarjetas perforadas para controlar de manera autom�tica el dise�o y los colores de los tejidos. Esta idea es adaptada a la computaci�n, en la llamada "m�quina anal�tica" (Figura 13), por un matem�tico ingl�s llamado Charles Babbage, quien vivi� obsesionado con el dise�o y construcci�n de m�quinas calculadoras. M�s adelante hablaremos de esta m�quina.
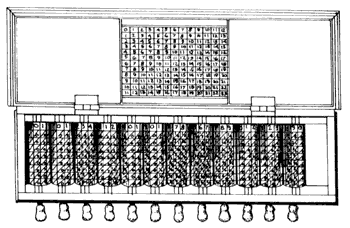
Figura 10. Esta figura muestra una variante de las "tablas de multiplicar", en la cual las tablas se ven substituidas por elementos que giran. Este aparato nunca lleg� a funcionar satisfactoriamente.
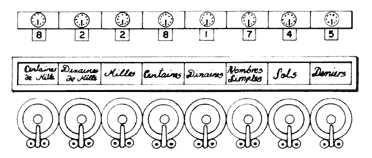
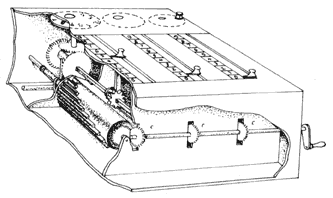
Figura 12. Diagrama que muestra un corte de la m�quina de calcular de Leibniz.
Babbage hizo su primer esbozo de una m�quina calculadora a la que llam� m�quina diferencial", en 1822. Sin embargo, constantemente ten�a nuevas ideas que mejoraban el dise�o original, por lo cual iba echando por tierra todo el trabajo realizado anteriormente. Es probable que esta situaci�n hubiese continuado por muchos a�os, de no ser por una discusi�n que tuvo con su mec�nico, despu�s de la cual este �ltimo desmont� el taller y parti� con todos los dise�os. En esta coyuntura, Babbage tiene que empezar un nuevo dise�o, y as� concibe una calculadora totalmente nueva: su "m�quina anal�tica", la cual habr�a de ser m�s f�cil de construir y tendr�a mayor poder de c�lculo que la anterior. As�, dise�a una computadora mec�nica digital a la cual habr�an de suministr�rsele datos e instrucciones a seguir a trav�s de tarjetas perforadas de acuerdo con un c�digo. La computadora a su vez proporcionar�a las soluciones tambi�n en forma de perforaciones en tarjeta. Como consecuencia, esta m�quina "programable" ofrec�a dos nuevas ventajas: i) por primera vez, una m�quina ser�a capaz de utilizar durante un c�lculo los resultados de otro anterior sin necesidad de reconfigurar la m�quina, lo cual permitir�a llevar a cabo c�lculos iterativos, y ii) habr�a la posibilidad de que la computadora siguiese instrucciones alternas, dependiendo de los resultados de una etapa anterior del c�lculo. Babbage describi� esta m�quina como "la m�quina que se muerde la cola".
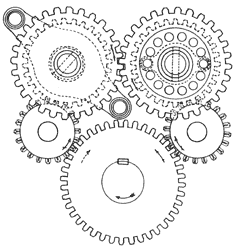
Figura 13. El dispositivo que se muestra en esta figura, forma parte de la m�quina anal�tica de Babbage y nos da idea de su complicaci�n; est� dise�ado para efectuar la operaci�n de leamirba
multiplicar ( o dividir) un n�mero por una potencia de diez.
Los planes de Babbage eran crear una m�quina de no menos de 20 cifras de capacidad y precisi�n de seis cifras. Probablemente, las debilidades m�s grandes de este dise�o fueron el cuidado y precisi�n requeridos para su construcci�n. De manera que, aunque su dise�ador dedic� el resto de su vida, y gran parte de su fortuna, a tratar de terminar esta m�quina, s�lo pudo hacer una versi�n peque�a del modelo. De haberse construido, la m�quina hubiese consistido de cerca de dos toneladas de maquinaria de relojer�a de lat�n y acero.
Para dar una idea al lector de la importancia de "la m�quina que se muerde la cola", diremos que hasta ese momento, cada vez que se quer�a efectuar una serie de operaciones matem�ticas, hab�a que introducir, una a una y manualmente, todas las instrucciones y datos de la operaci�n conforme se iban necesitando. A cada paso la m�quina iba dando el resultado parcial de la operaci�n espec�fica efectuada, de manera que el "usuario" de la m�quina pod�a decidir cu�l ser�a la siguiente operaci�n.
LA ERA MODERNA DE LA COMPUTACI�N
Con el desarrollo posterior de la electricidad aparecieron las llamadas computadoras electromec�nicas, las cuales utilizaban solenoides e interruptores mec�nicos operados el�ctricamente. La primera de ellas se cre� en 1944 y fue la llamada Mark I. Las instrucciones "se cargaban" por medio de cinta de papel con perforaciones, y los datos se proporcionaban en tarjetas de cart�n, tambi�n perforadas. Esta computadora ten�a aproximadamente 15.5 m. de largo por 2.5 de altura, y multiplicaba dos n�meros en aproximadamente 3 segundos. Tres a�os m�s tarde, la computadora Mark II. era capaz de llevar a cabo la misma operaci�n en menos de un cuarto de segundo; esto es, 12 veces m�s r�pido.
Mientras estas computadoras anal�gicas2![[Nota 2]](../imgs/mcommnt.gif){kind=small}
eran construidas, se gestaba un nuevo concepto de computadoras. �stas eran las
llamadas computadoras digitales, acerca de cuya paternidad existen gran
cantidad de disputas. Sin embargo, como narraremos a continuaci�n, en una batalla
legal en las cortes de los Estados Unidos de Am�rica se atribuy� el derecho
a llamarse "inventor de la computadora digital" a John V. Atanasoff, un
f�sico estadounidense, hijo de un ingeniero el�ctrico y una maestra de �lgebra.
Desde muy peque�o, Atanasoff encontr� gran placer en el estudio del �lgebra. Cuando ten�a 10 a�os de edad, su madre le dio un libro en el cual se explicaba c�mo calcular n�meros en otras bases diferentes a la base diez. A�os m�s tarde, Atanasoff comentar�a: "Cuando inici� mi trabajo en computadoras, una de las cosas que ten�a en mente era que tal vez las computadoras trabajar�an mejor si utilizaran para sus c�lculos alguna otra base que no fuese diez."
M�s adelante, Atanasoff estudi� ingenier�a el�ctrica e hizo estudios de posgrado en matem�tica y f�sica, para posteriormente llegar a ser profesor asociado de f�sica y matem�ticas en la Universidad de Iowa. Una de las motivaciones de Atanasoff para trabajar en el dise�o de computadoras fue su gran frustraci�n ante la incapacidad de sus alumnos para encontrar las soluciones de sistemas grandes de ecuaciones diferenciales simult�neas; ya que consideraba que el tiempo invertido en esta tarea les imped�a dedicarse a otros problemas m�s interesantes. Dicho sea de paso, la soluci�n de este problema matem�tico era imposible de obtener utilizando las calculadoras anal�gicas existentes en ese momento. Es en esta �poca cuando Atanasoff tuvo varias ideas muy brillantes que revolucionaron las m�quinas calculadoras y que de hecho hicieron posible el inicio de la era moderna de la computaci�n. Estas ideas fueron las siguientes:
1) El remplazo de los relevadores electromec�nicos por bulbos. Los relevadores electromec�nicos utilizados hasta ese momento eran una especie de interruptores que pod�an abrirse o cerrarse cientos de veces por minuto. Dada la naturaleza de este proceso, no pod�a llevarse a cabo con m�s rapidez. Por otro lado, los bulbos pueden prenderse y apagarse (conducen o dejan de conducir electrones), cientos de veces por segundo. Esto es, operan con una rapidez mucho mayor que los relevadores electromec�nicos.
2) La substituci�n del sistema decimal por el sistema binario. Tanto los circuitos electr�nicos como los relevadores electromec�nicos tienen dos estados posibles; esto es, pueden estar prendidos o apagados, lo cual puede estar representado por ceros y unos, respectivamente. Esto hace que sea m�s natural para una computadora efectuar c�lculos utilizando para ello un sistema num�rico binario.
3) La utilizaci�n de condensadores para construir dispositivos encargados de guardar informaci�n ("memorias"). Estos nuevos dispositivos estar�an formados por un gran n�mero de condensadores (tambi�n llamados capacitores), los cuales, al estar cargados o descargados, guardar�an informaci�n, de acuerdo con un c�digo binario. Sin embargo dado que es imposible lograr un aislamiento el�ctrico perfecto del dispositivo, era de esperarse que la carga se "escapar�a" en cuesti�n de milisegundos. Atanasoff ide� entonces un procedimiento llamado refrescamiento de memoria, el cual consiste en leer la informaci�n registrada en cada �rea de la memoria e inmediatamente reescribirla en el mismo lugar. Esta operaci�n deber�a llevarse a cabo peri�dica y autom�ticamente, a intervalos de tiempo regulares.
Durante los a�os subsecuentes, Atanasoff trabaj� junto con un estudiante en la construcci�n de un prototipo de computadora que utilizara estos principios, y que fue de hecho la primera en hacer aritm�tica electr�nicamente. �sta fue la llamada ABC (Atanasoff-Berry Computer), la cual utilizaba 300 bulbos para los circuitos l�gicos, y capacitores para la regeneraci�n autom�tica de la memoria. Por otro lado, mientras esto suced�a, Atanasoff firm� un convenio con la universidad en la que prestaba sus servicios. En dicho documento, el inventor conven�a en ceder a la universidad la mitad de las regal�as obtenidas por su computadora. A su vez, la universidad se compromet�a a tramitar la patente. Desafortunadamente, la universidad nunca cumpli� con su parte, aparentemente debido a negligencia y falta de confianza en este proyecto por parte de las autoridades.
Fue en est �poca, mientras trabajaba en el perfeccionamiento de la ABC, que Atanasoff tuvo su primer encuentro con un experto en computadoras llamado John Mauchly. Con esta persona tuvo largas discusiones acerca del tema que a ambos interesaba, le mostr� los principios de operaci�n de su computadora y le pidi� que guardara el secreto de su existencia hasta que �sta estuviese patentada. Fue entonces cuando estall� la segunda Guerra Mundial; Atanasoff fue llamado entonces a colaborar con la Fuerza Naval de su pa�s en un proyecto relacionado con la supervisi�n de pruebas ac�sticas de minas. Debido a estas circunstancias, se tuvo que abandonar el proyecto de la computadora ABC, por lo cual �sta nunca super� la etapa de pruebas.
La primera m�quina que lleg� a estar en plena operaci�n utilizando los principios ideados por Atanasoff fue la llamada ENIAC y fue �precisamente Mauchly! quien la construy� junto con otro colaborador llamado Presper Eckert. Esta computadora ten�a 19 000 bulbos, 1 500 relevadores, cientos de miles de capacitores, resistores e inductores, y aproximadamente 500 000 conexiones soldadas. Por otro lado, consum�a casi 200 kilovatios de potencia y llevaba a cabo una multiplicaci�n en 2.8 milisegundos (1 000 milisegundos = 1 segundo), esto es, �mil veces m�s r�pido que su predecesora, la computadora Mark II!
Aunque Mauchly sosten�a que esta computadora era totalmente diferente de la ABC, a�os m�s tarde la patente de la ENIAC fue invalidada. Despu�s de una batalla de demandas y contrademandas entre compa��as constructoras de computadoras, por no pagar los derechos de patente, Atanasoff, apoyado por la IBM, inicio un juicio contra la patente de la ENIAC. En este juicio, fue reconstruida la ABC y se demostraron los principios que �sta utilizaba en su funcionamiento. El 19 de octubre de 1973, 28 a�os despu�s de construida la ENIAC, el juez fall� en favor de Atanasoff. Sin embargo, esta noticia no tuvo el impacto que era de esperar, debido a que ese mismo d�a sali� a la luz el esc�ndalo de Watergate.
En a�os subsecuentes ha habido un desarrollo acelerado de las computadoras electr�nicas digitales: el invento del transistor y el avance posterior en la electr�nica han logrado una diferencia dram�tica en eficiencia y costos. As� se han logrado: un aumento en la rapidez con que se efect�an las operaciones matem�ticas, un aumento en la cantidad de informaci�n que es posible manejar y almacenar, la disminuci�n del volumen de las m�quinas, y la disminuci�n de su costo de operaci�n y mantenimiento. Para dar una idea de la magnitud de estos avances, diremos que una peque�a calculadora programable de bolsillo tiene, hoy d�a, el mismo o un mayor poder para hacer c�lculos que las voluminosas computadoras de principios de los a�os cincuenta, adem�s de estar al alcance de casi cualquier bolsillo y tener un costo de mantenimiento pr�cticamente nulo.
La historia reciente de la computaci�n se ha dividido en las llamadas generaciones de computadoras, cada una de las cuales est� caracterizada por un desarrollo o una innovaci�n importante. A continuaci�n haremos una breve rese�a de estas etapas.
�sta es la era de las computadoras construidas con bulbos; se inicia en 1951 con la primera computadora industrial, la llamada UNIVAC 1. Las computadoras de esta generaci�n eran muy grandes y de funcionamiento costoso. Los bulbos eran de gran tama�o y consum�an mucha energ�a el�ctrica, por lo que generaban mucho calor y se fund�an con frecuencia. Por lo anterior estas computadoras deb�an ser instaladas en cuartos con aire acondicionado, con el prop�sito de mantener el sistema lo m�s fr�o posible para disminuir la ocurrencia de fallas.
La segunda generaci�n de computadoras se inici�, a finales de los a�os cincuenta, con el remplazo de los bulbos por transistores. Los transistores son dispositivos electr�nicos �tiles para generar, amplificar y controlar se�ales el�ctricas. Si comparamos los bulbos con los transistores, podemos ver que estos �ltimos son mucho m�s peque�os, m�s confiables, generan menos calor y requieren menos energ�a para su operaci�n. Todo esto contribuy� a crear computadoras m�s peque�as, baratas y confiables. En esta �poca comenz� el auge de las computadoras desde el punto de vista comercial, se crearon muchas compa��as dedicadas a su dise�o y construcci�n.
Las m�quinas de la tercera generaci�n se distinguen por dos aspectos importantes: por un lado, su componente fundamental lo constituyen los circuitos integrados, y por otro, se forman las familias de computadoras caracterizadas por tener compatibilidad hacia arriba. A continuaci�n hablaremos de estos dos puntos.
Los circuitos integrados est�n formados por un elemento base de silicio (chip), con un gran n�mero de transistores y otras componentes integradas, interconectadas, que ocupan un espacio aproximado de 2.5 cm de largo por 1.25 cm de ancho. El uso de estos circuitos hizo a las computadoras m�s econ�micas, confiables, compactas y con un costo de operaci�n mucho m�s bajo. Todo esto, con respecto a las computadoras de generaciones anteriores.
Las familias de computadoras fueron creadas en un intento por lograr compatibilidad entre m�quinas de modelos diferentes, construidas por un mismo fabricante. Las computadoras de la segunda generaci�n ten�an el problema de que los programas escritos para m�quinas peque�as no pod�an ser utilizados por m�quinas m�s grandes (ni viceversa), aunque ambas fuesen producidas por la misma firma comercial. Al construirse m�quinas compatibles se dio un paso muy importante desde el punto de vista comercial y pr�ctico, ya que permiti� a peque�as empresas en desarrollo el ir adquiriendo m�quinas cada vez m�s poderosas seg�n el aumento de sus necesidades. De esta manera, los programas escritos para las m�quinas peque�as podr�an ejecutarse en m�quinas m�s grandes de la misma familia, haciendo, en el peor de los casos, tan s�lo peque�as modificaciones.
La cuarta generaci�n de computadoras se caracteriza por el uso del microprocesador. �ste consiste en un solo circuito integrado, el cual contiene en su totalidad a la unidad central de procesamiento (CPU), o cerebro de la computadora. En esta generaci�n, el mayor logro consisti� en hacer computadoras peque�as, con mayor poder y menor volumen y costo.
Actualmente se trabaja en la creaci�n de la quinta generaci�n de computadoras.
Esta nueva generaci�n seguramente incluir� dos cambios importantes. El primero
consiste en un cambio fundamental en la manera de efectuar el procesamiento
de la informaci�n, y por tanto, implica el dise�o de arquitecturas conceptualmente
diferentes.3 El
segundo cambio que esperamos, consiste en el desarrollo y adaptaci�n de nuevas
tecnolog�as.
Las computadoras convencionales procesan la informaci�n en serie, efect�an una instrucci�n despu�s de otra. Como consecuencia, la mayor parte de la computadora y de sus perif�ricos est�n ociosos gran parte del tiempo mientras esperan instrucciones del procesador central. Con el objeto de proceso, han sido dise�adas grandes m�quinas, llamadas supercomputadoras, cuyo prop�sito es llevar a cabo el procesamiento de la informaci�n en paralelo; esto es, constan de varios elementos procesadores, cada uno de los cuales efect�a tareas de manera independiente y simult�nea. De esta forma, el trabajo se divide en subtrabajos independientes, los cuales son asignados a diferentes elementos procesadores. Un ejemplo de estas m�quinas es la computadora modelo CRAY 1, la cual consta de 64 elementos procesadores.
Estas supercomputadoras paralelas tienen un costo de producci�n muy
alto, que se refleja en su costo de uso comercial;4 de
manera que existen muy pocas en el mundo. Debido a esto, en los Estados Unidos
de Am�rica se han organizado centros de supercomputaci�n en los cuales se da
servicio a un gran n�mero de usuarios, a trav�s de la l�nea telef�nica.
Adem�s de su elevado costo, este tipo de computaci�n presenta algunas inconveniencias: es dif�cil programar una computaci�n paralela, ya que el programador debe fraccionar el problema en peque�as tareas independientes, y optimizar la manera de asignarlas. Adem�s, la mayor parte de los problemas no son paralelos por naturaleza; es decir, no siempre es posible dividir un trabajo en subtrabajos independientes, o hacerlo de manera eficiente, pues algunos procesadores requieren de los resultados obtenidos por otros para poder continuar sus c�lculos. Como consecuencia, a menudo nos encontramos con que la m�s veloz supercomputadora opera casi a la misma velocidad que un procesador en serie. Este problema es conocido como el cuello de botella de Neumann.
En los �ltimos a�os, ha aparecido un nuevo concepto en la computaci�n, que probablemente proporcionar� una soluci�n a algunos de los problemas reci�n indicados. Este nuevo concepto, conocido con el nombre de redes neuronales, es radicalmente diferente al anterior: se utilizan elementos electr�nicos que emulan neuronas simplificadas, los cuales se conectan entre s� formando redes similares a las que se encuentran en el cerebro, aunque a una escala mucho menor. Recientemente, los investigadores dedicados al desarrollo de las redes neuronales han logrado resultados sorprendentes, y todo parece indicar que, en el futuro, estos dispositivos podr�n dotar a las computadoras de capacidades similares a las humanas para la soluci�n de problemas complejos. M�s adelante explicaremos las bases de las redes neuronales y discutiremos algunas de las perspectivas inmediatas en cuanto a su aplicaci�n a la computaci�n.
El segundo cambio que creemos caracterizar� a la quinta generaci�n de computaci�n
consiste en el desarrollo y adaptaci�n de nuevas tecnolog�as. No es posible
continuar reduciendo indefinidamente el tama�o de los circuitos integrados,
ni lograr que disipen menos energ�a, como tampoco es posible conseguir que los
electrones se transporten con mayor rapidez. Si se desea hacer una mejora substancial,
es necesario recurrir al desarrollo y adaptaci�n de nuevas tecnolog�as que ofrezcan
ventajas sobre las actuales. En este terreno, se avecina la era de las computadoras
�pticas, las cuales utilizar�n fuentes de luz coherente (rayos l�ser), lentes,
y fibras �pticas para transportar a los fotones a lo largo de trayectorias no
rectas. Por consiguiente, funcionar�n con base en el transporte de fotones y
no de electrones, como sucede en la actualidad. Por �ltimo, tal vez pronto veremos
reflejado en las nuevas computadoras el hallazgo reciente de materiales que
son superconductores a temperaturas relativamente altas (hasta ahora del orden
de -150°C). Lo cual significa que si estos materiales se mantienen por debajo
de una cierta temperatura, sus electrones son capaces de viajar sin disipar
energ�a y por lo tanto, sin producir calor.5
